-
오늘은 VAE. 그 중에서도 β-VAE의 특징과 사용하는 목적에 대해 정리하고자 한다.
-
참고논문
-
β-VAE: LEARNING BASIC VISUAL CONCEPTS WITH A
CONSTRAINED VARIATIONAL FRAMEWORK (2017)
| Higgins et al (2017) -
Addressing Posterior Collapse in Variational Autoencoders with -VAE
| Wang, Z. (2023)
-
VAE
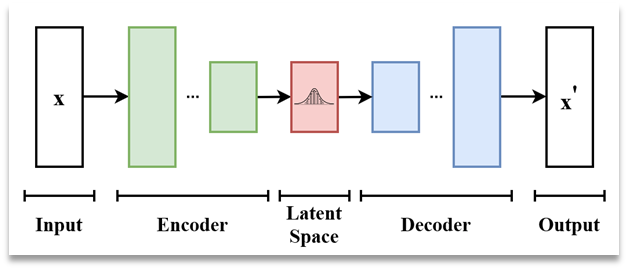 |출처: 위키백과
|출처: 위키백과
-
먼저 VAE는 위 그림과 같이 입력 데이터(x)를 인코더(또는 inference network)를 사용하여 압축한 뒤,
-
Latent variable Z를 사용하여 디코더를 통과한 출력 데이터(x')을 생성하는 일종의 생성 모델이다.
-
오토인코더(AE)와 다르게 latent variable에 표준정규분포를 따르는 노이즈를 추가함으로써, 역전파(backpropagation)을 가능하게 한다는 특징이 있다.
-
즉, 기존 AE에 비해 latent variable의 representation 성능을 높이는 특징이 있다.
reparameterization trick -
VAE에서 가장 흔히 사용하는 손실함수는 ELBO이다.
- ELBO(Evidence Lower Bound
- 재구성 손실 + KL 발산을 더한 값으로 구성된 값
- 재구성 손실이란, x와 x'간 차이를 계산하는 손실로, 보통 cross-entropy 사용
- KL발산이란, 분포의 차이를 계산하는 방법으로, VAE 학습 과정에서 prior 분포와 latent variable의 posterior 분포 간 차이를 계산하는데, 이것이 KL 발산 손실로 사용된다.
- ELBO(Evidence Lower Bound
β-VAE
-
VAE의 구조는 동일하지만 손실함수. ELBO를 구성하는 방법에서 차이가 있다.
- 기존 VAE -> 재구성 손실 : KL 발산 손실 = 1 : 1
- β-VAE -> 재구성 손실 : KL 발산 손실 = 1 : β
-
β-VAE의 장점은 Posterior collapse 현상 방지와, Disentangle representation을 유도하는 장점이 있다.
β-VAE 장점 (1) Posterior Collapse 방지
-
Posterior Collapse란,posterior. 즉, 인코더를 통해 압축된 latent variable의 분포가 prior와의 차이가 거의 없어지는(= 과도한 일반화)문제가 발생함을 의미한다.- 과도한 일반화는 뭐가 문제일까?
- 만약 posterior collapse가 발생하여 posterior가 미리 가정한 prior와 같아진다면,
입력 값(x)이 달라진다고 한들 latent variable은 x와 무관하게 prior에서 샘플링되는 것과 같기 때문에 x의 특징을 반영하지 못하는 문제 발생
- 만약 posterior collapse가 발생하여 posterior가 미리 가정한 prior와 같아진다면,
- 과도한 일반화는 뭐가 문제일까?
-
이러한 문제를 해결하기 위해 손실 가중치 비율을 조정하여 잘 학습되도록 만든 VAE의 파생 모델
β > 1 -> KL발산 손실에 더 강한 규제 (= prior에 더 가깝게)
0 < β < 1 -> 재구성 손실에 더 강한 규제(단, 명확한 β값 레퍼런스는 없는 것 같고 실험으로 선택)
β-VAE 장점 (2) Entangled Representation 방지
-
Entangled Representation이란,
latent variable의 차원 간 정보가 서로 의존적(dependent)인 것을 의미차원 간 depentent가 왜 문제가 될까?- 이는 '생성' 측면에서 문제가 되는데,
만약 latent variable의 한 차원을 조작했을 때 생성한 결과물은 하나의 의미 있는 속성만 변해야 정상적인데, 만약 dependent하다면 조작의 결과가 매번 달라져 의미가 없게 됨
- 이는 '생성' 측면에서 문제가 되는데,
-
반대로 Disentengled representation은 latent variable의 각 차원 간 독립적(independent)인 특징을 갖는다고 할 수 있다.
※ 주의 ※
entangled라고 무조건 단점이 아니라 목적과 task에 따라 장점이 될 수도 있고 단점이 될 수 있으니 내가 무엇을 하려고 하는 건지 파악하는 게 우선이다.

