
-
오늘은
LSTM에 대해 정리해보자!
LSTM
LSTM 특징 및 요소
-
LSTM은 RNN의 파생 모델 중 하나로,
망각 게이트,입력 게이트,셀 상태 후보,출력 게이트를 사용 -
RNN에서 발생하는
장기 의존성(Long term dependency)문제 즉, 기울기 소실(Vanishing gradient)를 해결하기 위해 고안된 모델! -
LSTM은 아래 기능을 사용하여 RNN의 한계를 해결한다.
-
셀 상태(cell state)- 망각, 입력, 출력 게이트를 통해 정보가 오랜 구간 걸쳐도 손실되지 않도록 모델을 설계
- 전체 모델에 CEC(Constant error Carousel) 제공(=error의 기울기 소실/폭발 되지 않도록)
기울기 전파의 통로 역할
-
게이트 매커니즘- 망각 게이트(forget gate)
: 함수를 통해 0과 1 사이의 값을 출력하여, 이전 step의 cell state를 얼마나 잊을지, 또는 기억할지 결정
- 입력 게이트(input gate)
: 함수를 통해 0과 1 사이의 값을 출력하여 새로 생서된 셀 후보 중 얼마나 많이 현재 cell state에 반영할지 비율을 결정
- 출력 게이트(output gate)
: cell state의 정보를 얼마나 많이 필터링하여 은닉 상태로 내보낼지를 결정(=현재 step의 은닉 상태를 최종으로 결정)
- 망각 게이트(forget gate)
-
『주의』
- 은닉 상태와 셀 상태는 다른 개념
- 역할 특징 cell state 장기기억 기울기 소실 방지를 위한 CEC 역할 hidden state 단기기억 현재 시점 출력 and 다음 시점 게이트에도 사용됨
LSTM 내부 구조
(그림 출처 : https://wikidocs.net/book/6651)
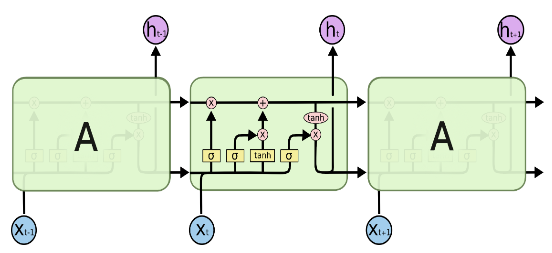 위 그림은 LSTM의 내부 구조를 나타낸다
위 그림은 LSTM의 내부 구조를 나타낸다
망각 게이트
-
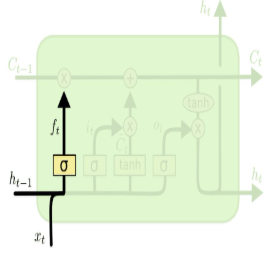 망각 게이트는 이전 시점의 hidden state와 새로운 입력 간 연산을 통해 정보를 생성하고 함수를 사용하여 cell state에 얼마나 반영할 지 결정한다.
망각 게이트는 이전 시점의 hidden state와 새로운 입력 간 연산을 통해 정보를 생성하고 함수를 사용하여 cell state에 얼마나 반영할 지 결정한다. -
즉, 과거 시점의 정보 반영 비율을 결정하는 게이트
-
연산 과정은 아래와 같다.
- 각 W는 가중치이고, X_t는 새로운 입력 벡터, h_t-1는 이전 시점의 hidden state를 의미
(f_t : 망각 게이트 활성화 값)
- 각 W는 가중치이고, X_t는 새로운 입력 벡터, h_t-1는 이전 시점의 hidden state를 의미
-
f_t와 이전 시점의 cell state를 곱하여 현재 cell state에 얼마나 반영할 지 결정
입력 게이트
-
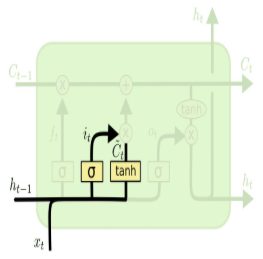 입력 게이트는 새로 들어온 정보를 얼마나 반영할지 결정하여 중요 정보 선별할 수 있다.
입력 게이트는 새로 들어온 정보를 얼마나 반영할지 결정하여 중요 정보 선별할 수 있다. -
입력 게이트 연산은 셀 후보 계산, 입력 게이트 활성화 값 계산으로 구성
-
먼저 셀 후보(cell candidate)를 계산
- 이는 현재 시점에서 새로운 정보의 후보를 생성하는 과정
-
셀 후보의 반영을 비율을 결정할 입력 게이트 활성화 값은 아래와 같이 계산
각 차원 별로 새로운 정보 후보의 반영 비율을 결정
-
앞서 망각 게이트의 연산 결과와 입력 게이트의 연산 결과를 기반으로 현재 cell state를 업데이트 한다.
출력 게이트
-
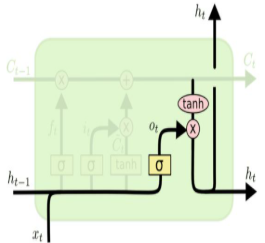 출력 게이트는
출력 게이트는 얼마만큼의 정보를 꺼내어 다음 시점으로 내보낼지 조절 -
불필요한 정보가 포함되는 것을 방지하는 역할
- 매 시점마다 전체 정보를 사용하기엔 불필요한 정보도 포함되기 때문에
-
출력 게이트의 연산
- 출력 게이트 활성화 값과 현재 시점의 cell state 연산 통해
현재 시점의 은닉 상태(hidden state)를 결정
- 출력 게이트 활성화 값과 현재 시점의 cell state 연산 통해
정리
- LSTM의 주요 3가지 게이트는
-
망각 게이트
-
입력 게이트
-
출력 게이트
-
- 망각 게이트
- 이전 시점의 cell state에서 정보를 얼마나 잊을지 결정
- 입력 게이트
- 새로운 정보를 현재 시점의 cell state에 얼마나 반영할지 결정
- 출력 게이트
- 현재 시점의 cell state에서 정보를 얼마나 꺼내어 현재 시점의 hidden state를 생성할지 결정
