회귀를 배우는 이유
- 회귀는 경사하강법에 대한 깊은 이해를 가능하게 해주기 때문에 알아가고 넘어가면 좋습니다!
회귀란?
그렇다면 회귀란 무엇일까요?
회귀는 여러 개의 독립 변수와 한 개의 종속 변수간의 상관관계를 모델링하는 기법입니다!
예를 들어 여러 특징들에 따른 집값에 대해 알아볼 때, 독립 변수에는 방 개수, 집 크기, 주변 학군 등이 있을 수 있고, 종속 변수는 집값입니다!
또한, 독립 변수의 값에 영향을 미치는 회귀 계수로, 딥러닝의 목적인 가중치에 해당합니다!
simple regression (단순 선형 회귀)
- 단순 선형 회귀는 독립 변수 1개만 사용하여 회귀 모델링하는 방법입니다!
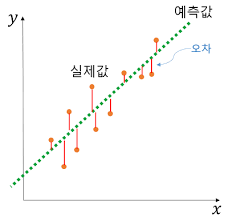
독립 변수를 집 크기 1개를 사용하여, 집값을 모델링하면 위와 같은 그래프가 나올 수 있습니다!
여기에서 y 절편을 bias라고 칭하고, W0에 해당됩니다.
위의 그래프에서 보이듯이, 각각실제 값과 예측 값의 차이들의 합이 최소가 되는 모델을 만드는 것이
최적의 회귀 모델을 만드는 것입니다.
그러기 위해선, 회귀 계수를 찾아내는 것이 목적이겠죠???
(집 크기라는 독립 변수를 조정할 수는 없으니, 회귀 계수를 조정하여 최적의 모델을 찾아내는 겁니다!)
여기서 오류 값을 잔차라고도 부릅니다.
RSS(residual sum of square)
- 잔차의 합을 쉽게 구하기 위해서 사용하는 방식입니다.
- 만약 실제값과 예측값의 차이가 5인 것과, -5인 것이 그대로 더해지면 오류가 0인 것으로 되므로, 이를 방지하기 위해 사용합니다! (절대값을 이용하기도 하지만, 이는 미분이 어려워 RSS를 사용!)
RSS 특징
- 실제 값과 예측 값의 차이를 제곱하여 다 더하는 것입니다 !
( 미분 등을 쉽게 할 수 있고, 실제값 - 예측값이 음수가 나오는 것을 방지) error의 제곱 == RSS- RSS는
W(가중치)변수가 중심변수임을 인지! (따라서 나중에 미분을 할 때, W(가중치)에 대해서 미분) - RSS를 학습 데이터의 건수로 나누어서
MSE로 표현 가능합니다!
MSE : 비용함수
- 비용 함수 : 오류 제곱의 평균 ~ 오류의 평균
- 머신러닝 알고리즘에서 회귀 알고리즘은 이 MSE를 지속해서 감소시키고, 더 이상 감소하지 않는 최소의 오류값을 구하는 것입니다!
