출처(sources) 및 참고
들어가면서
인덱스에 대해 공부하다보면 B-Tree 라는 용어를 굉장히 많이 보게 된다.
이는 인덱스를 이루는 자료 구조로 B-Tree를 많이 사용하기 때문인데 MySQL 8.0을 기준으로 InnoDB Engine 도 spatial indexes 를 제외하면 인덱스를 위한 자료 구조로 B-Tree 를 사용한다. (spatial indexes 의 경우 R-Tree 를 사용한다.)
실제 MySQL 의 InnoDB Storage Engine Indexes 문서를 보면 아래와 같은 문장이 적혀있다.
The Physical Structure of an InnoDB Index
With the exception of spatial indexes, InnoDB indexes are B-tree data structures. Spatial indexes use R-trees, which are specialized data structures for indexing multi-dimensional data.
출처 : MySQL Reference Menual - The Physical Structure of an InnoDB Index
인덱스를 공부하면서 "인덱스를 구성하기 위한 자료 구조로 B-Tree 를 사용하는 구나만 알고 넘어가면 되지 않아?"라고 할 수도 있다. 물론 그럴 수도 있다. 하지만 B-Tree의 동작 방식을 알아가면서 왜 인덱스 사용시 Insert, Update, Delete 연산의 성능이 저하될 수 있는지 조금 더 깊이있게 이해할 수 있게 된다.
자, 그럼 우선 B-Tree 에 대해 알아가보도록 하자!
P.S 보통 InnoDB Storage Engine 을 많이 사용하기에 MySQL 8.0 버전의 InnoDB Storage Engine을 기준으로 작성합니다.
그리고 B-Tree 의 동작 과정을 웹에서 시각화해주는 사이트가 있습니다. 이것을 이용해 M차 B-Tree 의 데이터 데이터 삽입, 삭제, 조회 과정을 살펴보시는 것도 도움이 될 것 같습니다!
B-Tree
위키 백과에서는 B-Tree 를 아래와 같이 소개하고 있다.
전산학에서 B-트리(B-tree)는 데이터베이스와 파일 시스템에서 널리 사용되는 트리 자료구조의 일종으로, 이진 트리를 확장해 하나의 노드가 가질 수 있는 자식 노드의 최대 숫자가 2보다 큰 트리 구조이다.
출처 : https://ko.wikipedia.org/wiki/B_%ED%8A%B8%EB%A6%AC
즉, B-Tree는 이진 트리를 확장한 트리이지만 이진 트리와는 다르게 자식 노드의 개수를 2개 이상 가질 수 있는 트리인 것이다. (=> 이진 트리는 아니다.)
그리고 조금 더 설명하자면 B-Tree는 AVL Tree, Red-Black Tree 등과 같은 균형 트리(Balanced Tree)의 일종이며 이진 탐색 트리(Binary Search Tree)와 비슷하게 아래의 조건이 지켜져야한다.
- 특정 노드의 각 데이터 D(k) 의 왼쪽 서브 트리는 D(k)의 값보다 작은 값을 가져야한다.
- 특정 노드의 각 데이터 D(k) 의 오른쪽 서브 트리는 D(k) 값보다 큰 값을 가져야한다.
참고로 B-Tree 의 시간 복잡도는 O(logN) 이다. 이진 트리의 경우에는 최악의 경우 O(N)이 되어진다.
B-Tree의 특징 및 규칙
B-Tree의 조건에 대해 먼저 정리하고 B-Tree의 구조와 동작 방식에 대해 더 깊게 알아보자!
[설명에 사용될 문자]
M : 하나의 노드가 가질 수 있는 최대 데이터 개수.
N : 하나의 노드에 존재하고 있는 현재 데이터의 개수.
1. 하나의 노드에 여러 개의 데이터가 존재할 수 있는 트리 자료 구조이다.
- 이진 트리의 경우 하나의 노드에 하나의 데이터만 존재한다.
2. 하나의 노드에 최대 M개의 데이터가 존재할 때, 이를 M차 B-Tree 라고 한다.
- 예를 들어 하나의 노드가 최대 5개의 데이터를 가질 수 있다면 이를 5차 B-Tree, 최대 10개를 가질 수 있다면 이를 10차 B-Tree 라고 한다.
- M차 B-Tree라고 해서 반드시 모든 노드가 항상 M개의 데이터를 가지고 있다는 것은 아니다. 하나의 노드가 최대 M개까지의 데이터만 저장할 수 있다는 말이다.
- 최대 데이터 수 M이 짝수인가, 홀수인가에 따라 알고리즘에 차이가 존재한다.
3. 특정 노드에 존재하는 데이터의 수가 N이라고 할 때, 해당 노드의 자식 노드의 수는 반드시 N+1개이어야 한다.
- 당연히 N은 M 보다는 작거나 같아야한다. N <= M
- 예를 들어 N 이 3이라면, 자식 노드의 개 수는 반드시 N+1인 4가 되어야하는 것이다.
4. 각 노드의 자료는 정렬된 상태여야 한다.
- 하나의 노드 안에 존재하는 데이터는 모두 정렬된 상태여야 한다.
- 예를 들어 하나의 노드 안에 [2, 3, 1, 4, 5]의 값이 존재해야 한다면 이는 노드 안에서 [1, 2, 3, 4, 5]의 순서로 정렬되어있어야 한다.
5. 특정 노드에 존재하고 있는 각 데이터를 D(k) 라고 표현할 때, D(k)의 왼쪽 서브 트리는 D(k)보다 작은 값들로 구성되어야 하고, 오른쪽 서브 트리는 D(k)의 값보다 큰 값들로 이루어져야 한다.
- 예를 들어 부모 노드에 존재하는 첫번째 데이터 D(1)을 5라고 할 때, D(1)의 왼쪽 서브 트리는 5보다 작은 값을 가져야하고, D(1)의 오른쪽 서브트리는 5보다 큰 값을 가져야한다.
6. Root Node는 적어도 2개 이상의 자식 노드를 가져야한다.
- Root Node 단일로 존재할 때는 해당 사항이 없지만, Root Node 가 Child Node 를 가져야한다고 했을 때는 반드시 2개 이상의 자식 노드를 가져야한다.
- 즉, Root Node 는 자식 노드를 1개만 가질 수는 없다는 것이다. 왜냐하면 3번 규칙을 보면 "특정 노드에 존재하는 데이터의 수가 N이라고 할 때 해당 노드의 자식 노드의 수는 N+1이다."라고 했다. 따라서 Root Node 가 1개의 자식 노드만 가진다는 것은 말이 안된다.
7. Root Node를 제외한 모든 노드는 적어도 M/2개의 데이터를 가져야한다.
- M=4 라고 할 때, Root Node 를 제외한 모든 노드는 적어도 4/2 즉, 2개의 데이터를 가지고 있어야한다.
- M이 홀수일 경우에는 소수점이 남게 되는데 이때 소수점은 버린다.
예를 들어 M=5 라고 할 때, Root Node 를 제외한 모든 노드의 데이터 수는 2.5(5/2)개가 되는데 이때, 소수점 아래의 수는 버리고 2만 남긴다는 것이다.
따라서 M=5 일 때 Root Node 를 제외한 모든 노드는 2개의 데이터를 가지고 있어야한다.
8. 모든 Leaf Node 는 반드시 같은 레벨(Level)에 존재해야 한다.
- 레벨(Level)이란 트리의 특정 깊이를 가지는 노드의 집합을 의미한다.
- 트리의 깊이란 Root Node 에서 특정 노드까지 도달하기 위해 거쳐야하는 간선의 수를 의미한다.(간선 : 노드와 노드를 연결하는 연결선)
- 즉, "모든 Leaf Node 는 반드시 같은 레벨에 존재해야한다"는 의미는 Root Node 에서 Leaf Node 까지의 깊이가 모두 같아야 한다는 것으로도 이해할 수 있다.
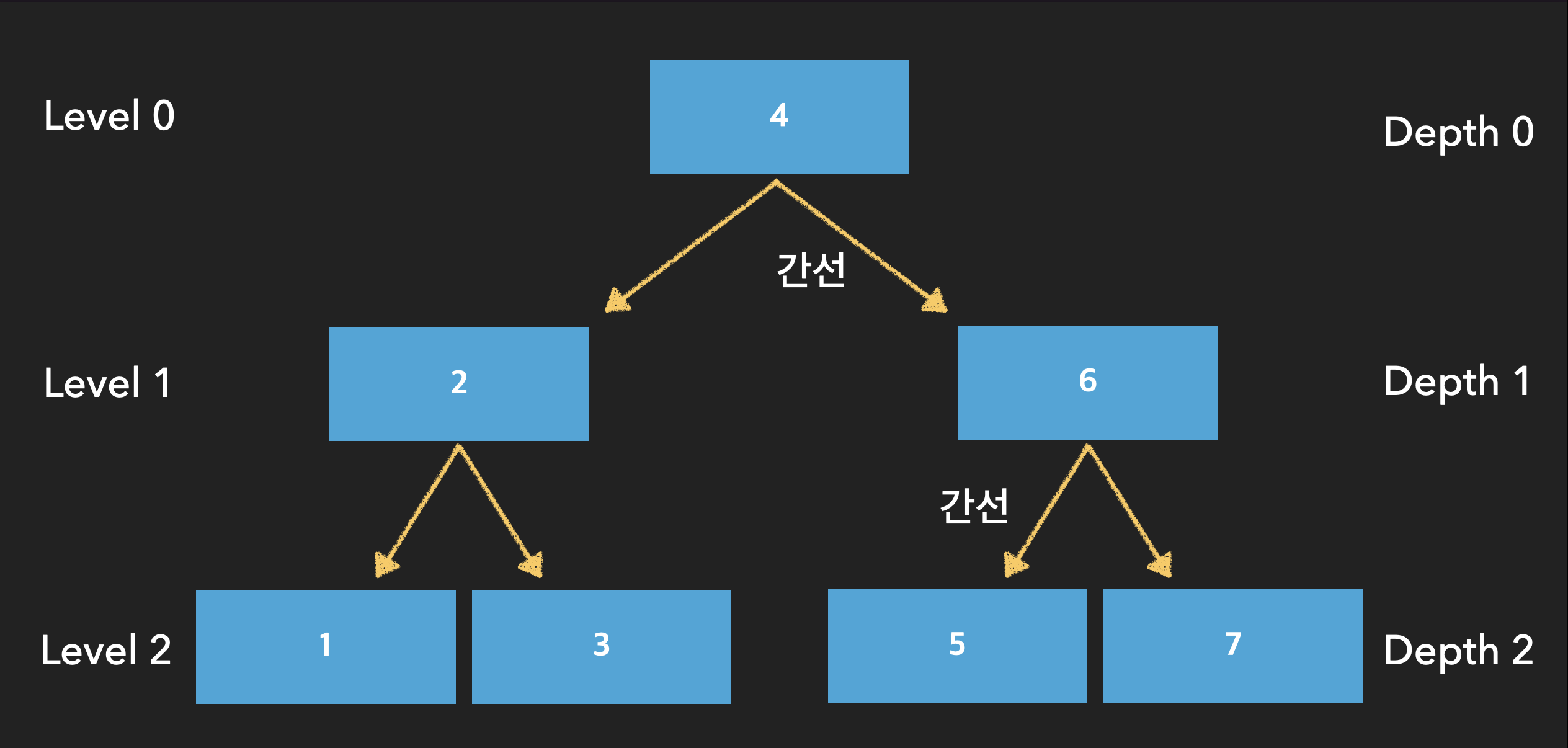
- 위의 그림은 3차 B-Tree 인데, 그림에서 볼 수 있듯 모든 Leaf Node의 레벨(Level)은 2이다. 그리고 깊이(Depth)로 보자면 이것 또한 2로 동일하다.
9. B-Tree 안에 존재하는 데이터는 중복될 수 없다.
- B-Tree 안에 [1, 2, 3, 4, 5] 라는 값이 존재한다고 해보자. 이때 만약 3을 입력한다고 하면 이미 3이라는 값이 존재하기 때문에 3은 입력되어서는 안된다.
- 물론 중복된 값을 허용하기 위해 List 와 같은 자료 구조를 사용하게 된다고 하면 가능할 수는 있겠지만 원칙적으로 B-Tree 는 데이터의 중복을 허용하지 않는다.
B-Tree 의 기본 구조
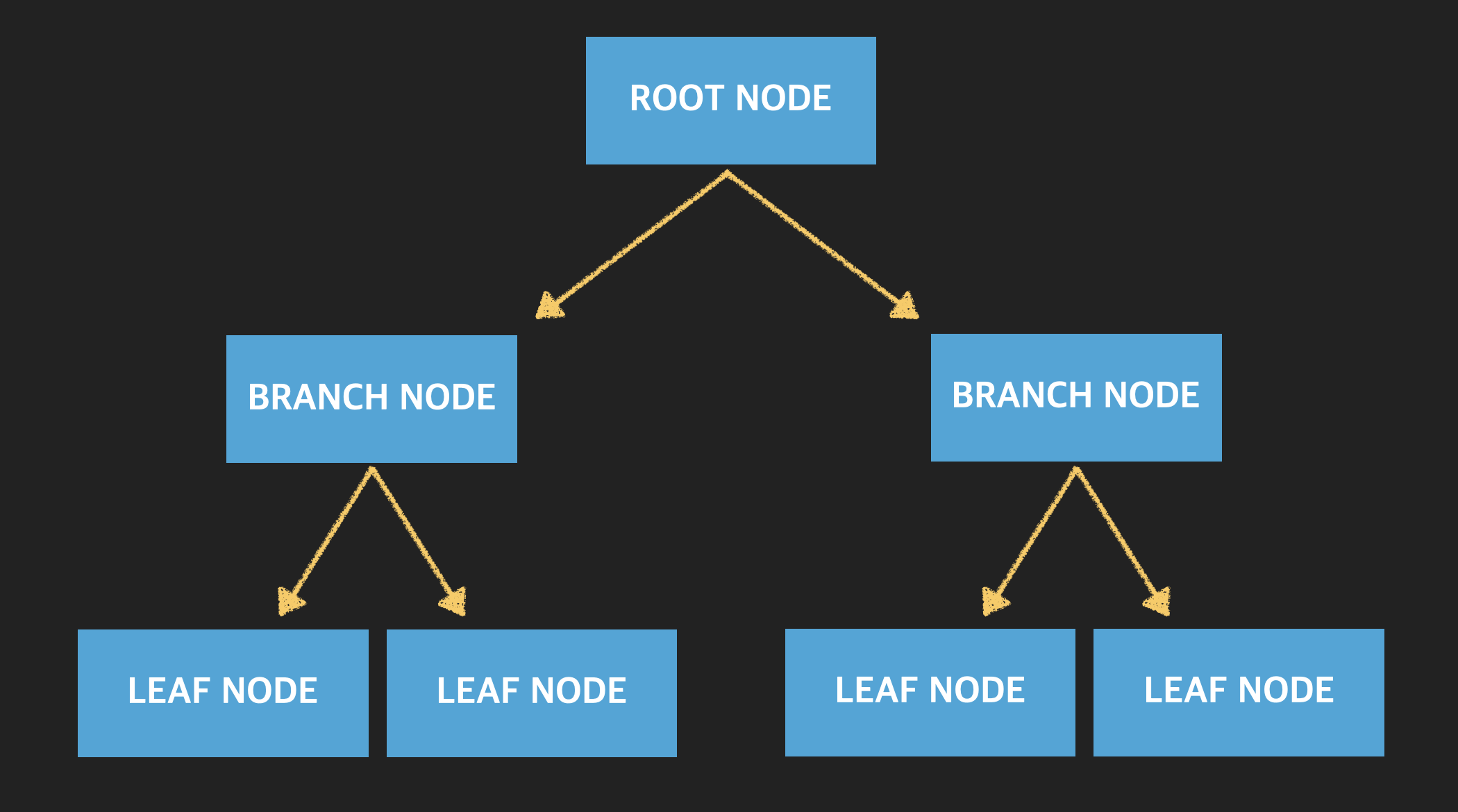
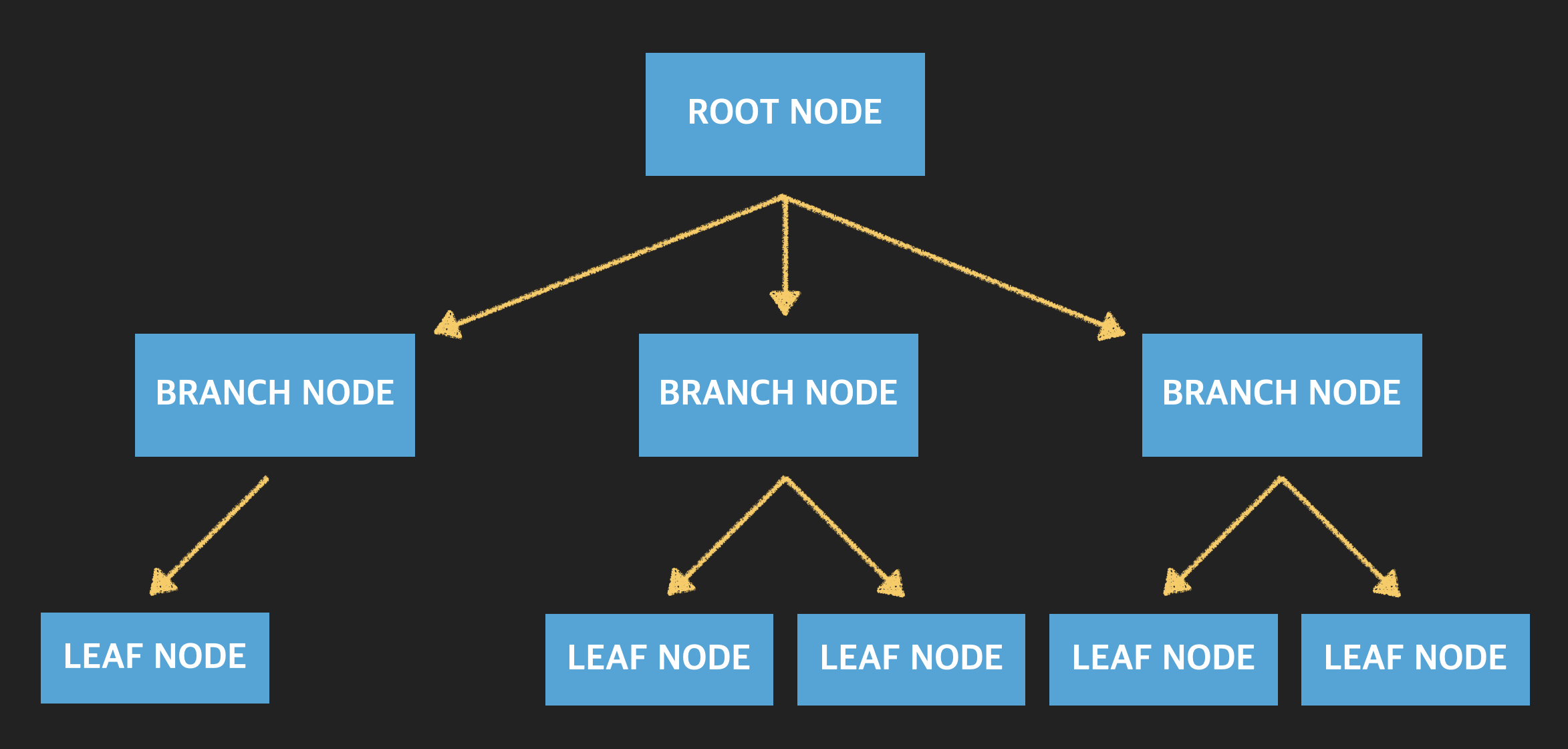
B-Tree 의 기본적인 구조는 위의 이미지와 같다.
최상위 노드(페이지)를 Root Node 라 하며 가장 아래에 위치하는 노드를 가리켜 Leaf Node 라 한다. 그리고 Root Node 와 Leaf Node 사이에 존재하는 노드를 가리켜 Branch Node 라고 한다.
노드란 데이터가 존재하는 공간을 의미하는데 페이지(Page) 라고도 불리운다.
정리
- MySQL 8.0 을 기준으로 InnoDB Storage Engine 은 인덱스를 위한 자료 구조로 B-Tree 를 사용한다.
- Spatial indexes (공간 인덱스) 의 경우에는 R-Tree 를 사용한다.
- B-Tree란
- 이진 트리를 확장한 트리이다. 그러나 자식 노드의 개수를 2개 이상 가질 수 있는 트리이다.
- 균형 트리(Balenced Tree)의 일종이다.
- 시간 복잡도는 O(logN) 이다.
- B-Tree 의 특징 및 규칙
- 하나의 노드에 여러 개의 데이터가 존재할 수 있는 트리 자료 구조이다.
- 하나의 노드에 최대 M개의 데이터가 존재할 때, 이를 M차 B-Tree라고 한다.
- 특정 노드에 존재하는 데이터의 수가 N이라고 할 때, 해당 노드의 자식 노드의 수는 반드시 N+1개이어야 한다.
- 각 노드의 자료는 정렬된 상태여야 한다.
- 특정 노드에 존재하고 있는 각 데이터를 D(k) 라고 표현할 때, D(k)의 왼쪽 서브 트리는 D(k)보다 작은 값들로 구성되어야 하고, 오른쪽 서브 트리는 D(k)의 값보다 큰 값들로 이루어져야 한다.
- Root Node는 적어도 2개 이상의 자식 노드를 가져야한다.
- Root Node를 제외한 모든 노드는 적어도 M/2개의 데이터를 가져야한다.
- 모든 Leaf Node 는 반드시 같은 레벨(Level)에 존재해야 한다.
- B-Tree 안에 존재하는 데이터는 중복될 수 없다.
- B-Tree 의 기본 구조
- 가장 맨 위에 있는 노드를 가리켜 루트 노드(Root Node)라고 한다.
- 가장 맨 아래에 있는 노드를 가리켜 리프 노드(Leaf Node)라 한다.
- 루트 노드와 리프 노드 사이에 존재하는 노드를 가리켜 브랜치 노드(Branch Node) 라고 한다.
참고
이진 트리(Binary Tree)
이진 트리란 아래의 두 조건을 만족하는 트리 자료 구조이다.
- 루트 노드(Root Node)를 중심으로 두 개의 서브 트리(Sub Tree)로 나뉘어진다.
- 나뉘어진 두 서브 트리(Sub Tree)도 모두 이진 트리이어야 한다.
이진 탐색 트리(Binary Search Tree)
이진 탐색 트리란 이진 트리에 데이터의 저장 규칙을 추가해놓은 이진 트리이며 동시에 아래와 같은 조건을 만족하는 이진 트리이다.
- 이진 탐색 트리의 노드에 저장된 키(key)는 유일하다.
- 루트 노드(Root Node)의 왼쪽 서브 트리(Sub Tree)를 구성하는 모든 노드의 키(Key)는 루트 노드의 키(Key)보다 작다.
- 루트 노드(Root Node)의 오른쪽 서브 트리(Sub Tree)를 구성하는 모든 노드의 키(Key)는 루트 노드의 키(Key)보다 크다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
