출처(sources) 및 참고

• B-Tree visualization

들어가기 전에

만약 B-Tree의 개념에 대해 잘 모른다면 👉 B-Tree의 개념에 대해 읽어보고 오자!

B-Tree의 데이터 삽입 과정은 상향식으로 진행된다.
즉, B-Tree의 데이터 삽입은 항상 리프 노드(Leaf Node)에서 시작된다는 것이다.
자! 그럼 B-Tree의 데이터 삽입 과정을 살펴보자.

---

B-Tree의 데이터 삽입 과정

B-Tree의 데이터 삽입의 과정을 큰 틀에서 아래와 같은 순서로 이루어진다.

1. 새로운 데이터를 삽입하기 위한 리프 노드를 탐색한다.

2. 리프 노드 발견시 새로운 데이터를 추가한다.

B-Tree의 규칙을 보면 알 수 있지만 루트 노드를 제외한 다른 노드(브랜치 노드)는 반드시 리프 노드(Leaf Node)를 가지게 된다.

[규칙 기억해보기]
👉 특정 노드에 존재하는 데이터의 수가 N이라고 할 때, 해당 노드의 자식 노드 개수는 반드시 N+1개이어야 한다.

3. 새로운 데이터 추가 후 필요하다면 노드의 분할(Split)과 병합(Merge)을 수행한다.

노드의 분할과 병합은 경우에 따라 분할만 수행될 수도 있고 분할과 병합 모두 수행될 수도 있다.
물론 분할과 병합 모두 수행되지 않을 수도 있다.
분할과 병합은 필요한 순간에만 수행된다.

일단 분할과 병합이 무엇인지, 그리고 분할과 병합이 모두 수행되지 않는 경우, 분할만 수행되는 경우, 분할과 병합 모두 수행되는 경우에 대해 살펴보자.

---

노드의 분할(Split)과 병합(Merge)

B-Tree는 하나의 노드가 가질 수 있는 최대 데이터의 개수가 존재한다고 했다.
이를 M이라고 표현해보자.

M : 하나의 노드가 가질 수 있는 최대 데이터 개수

그리고 노드의 분할은 특정 노드에 존재하는 데이터 개수가 M과 같아졌을 때 발생한다고 가정하자.(구현에 따라 다를 수 있기 때문.)

노드의 분할(Split)

B-Tree의 특정 리프 노드의 데이터 수가 M이 될 때, 해당 리프 노드의 데이터들 중 중간 값을 기준으로 해당 값보다 작은 값을 왼쪽 노드로, 큰 값을 오른쪽 노드로 분할하여 트리를 재구성하는 과정을 의미한다.

예를 들어 위의 B-Tree가 3차 B-Tree 이고 여기에 3을 새롭게 추가할 때 해당 노드는 아래와 같은 모양으로 바뀌게 되는데 이를 노드의 분할이라고 한다.

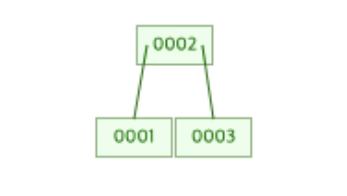
분할된 노드의 최종 모습을 보면 중간 값인 2를 루트 노드로 하여 2보다 작은 값은 왼쪽 노드로, 큰 값은 오른쪽 노드로 분할된 트리의 모습임을 알 수 있다.

노드의 병합(Merge)

만약 분할이 일어나는 노드가 루트 노드가 아닐 경우, 해당 노드는 반드시 리프 노드이다.
(사실 트리에 루트 노드만 존재할 경우 루트 노드는 루트 노드이면서 리프 노드이다.)
따라서 해당 노드는 반드시 부모 노드를 가지게 된다.
그러므로 리프 노드가 분할의 과정을 거치면서 재구성된 해당 서브 트리의 루트 노드는
기존 자신의 부모 노드와 합쳐지는 과정을 거치게 되는데 이를 노드의 병합이라고 한다.

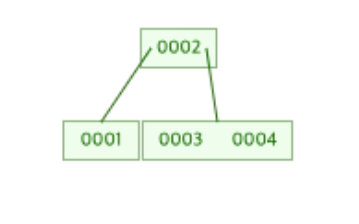
예를 들어 위와 같은 B-Tree가 존재하고 이것이 3차 B-Tree라고 했을 때, 여기에 5를 추가하게 되면 [3, 4]가 저장된 리프 노드에 5가 먼저 추가되어진다.

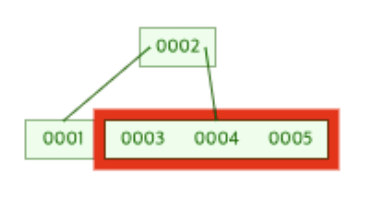
그리고 해당 노드의 데이터 개수는 M개가 되므로 [3, 4, 5]를 가지게 된 리프 노드는 분할의 과정을 거치게 된다.
[3, 4, 5]를 가진 리프 노드의 분할 과정만 떼어놓고 본 그림은 아래와 같다.

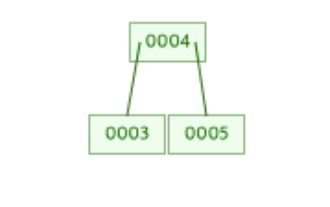
위의 그림을 통해 알 수 있듯 분할 과정을 거친 리프 노드([3, 4, 5])는 하나의 루트 노드와 2개의 리프 노드로 이루어진 트리의 모습으로 재구성된다.
이때 이 해당 트리의 루트 노드인 4는 [2]가 저장된 부모 노드와 합쳐져야 하는데 이를 노드의 병합이라고 한다. 최종 모습은 아래와 같다.

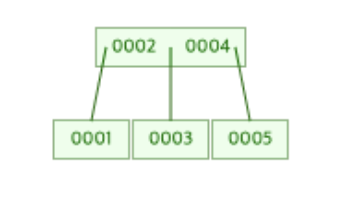
이렇게 함으로써 우리는 B-Tree의 규칙 중 "모든 Leaf Node 는 반드시 같은 레벨(Level)에 존재해야 한다."라는 규칙을 만족시킬 수 있다.
(이외에 다른 B-Tree의 규칙도 만족하게 되어진다.)

그리고 좀 더 생각해보면 노드의 병합은 리프 노드가 루트 노드가 아닐 경우
즉, 부모 노드가 존재할 경우 해당 리프 노드의 분할 과정 후에 발생한다는 것을 알 수 있다.

• 리프 노드의 분할 수행
• 리프 노드의 부모 노드가 존재하였는가?(해당 리프 노드가 루트 노드가 아닌가?)
  • TRUE => 리프 노드가 재구성된 트리의 루트 노드와 부모 노드를 합친다.
    (노드의 병합 과정에서 [2]를 가진 부모 노드와 노드의 분할 후 [4]를 가진 서브 트리의 루트 노드가 합쳐지는 과정)
  • FALSE => 부모 노드가 없다면 해당 리프 노드는 루트 노드이므로 분할의 과정만 거친 후 종료.

---

노드의 분할(Split)과 병합(Merge)의 발생 케이스

위에서 노드의 분할과 병합은 모두 일어날 수도 있고, 반대로 모두 일어나지 않을 수도 있다고 했다.
그리고 분할만 수행되어질 수도 있다고 하였다.
각각의 경우에 대해 살펴보자.

[설명에 사용될 문자]
M : 하나의 노드가 가질 수 있는 최대 데이터 개수

1. 분할과 병합 모두 수행되지 않는 경우

데이터 삽입을 위한 노드의 탐색 과정으로 발견된 리프 노드가 새로운 데이터 삽입 후에도 M보다 작은 데이터 개수를 가지게 된다면 노드의 분할이 발생하지 않는다.
따라서 노드의 병합 과정 또한 발생하지 않는다.
뒤에서 살펴보겠지만 노드의 병합은 분할이 선행된 후에 발생하게 된다.

2. 분할만 수행되는 경우

데이터 삽입을 위한 노드의 탐색 결과로 발견된 리프 노드가 M개의 데이터를 가지게 될 때 노드 분할의 과정이 이루어지게 된다고 하였다.
이때 루트 노드의 경우 부모 노드가 존재하지 않기 때문에 분할로 인한 부모 노드와의 병합 과정이 불필요하다.
따라서 루트 노드의 경우에는 노드의 분할만 수행되게 된다.
(사실 여기서 루트 노드는 루트 노드이면서 부모 노드가 존재하지 않는 리프 노드(Leaf Node)이다.)

3. 분할과 병합 모두 수행되는 경우

데이터 삽입을 위한 노드의 탐색 결과로 발견된 노드가 루트 노드가 아니라면 해당 노드는 반드시 리프 노드(Leaf Node)이다.
리프 노드의 경우 부모 노드가 존재하게 되는데 이때 리프 노드의 분할이 일어난다면 분할로 인해 재구성된 서브 트리의 루트 노드는 부모 노드와 병합이 일어나야 한다. (위에서 살펴보았다.)
그리고 이와 같은 분할과 병합의 과정은 최악의 경우 리프 노드부터 루트 노드까지 이어질 수 있다.

그럼 아래의 내용에서 그림을 보며 조금 더 쉽게 이해해보자.

---

노드의 분할(Split)과 병합(Merge) 그림을 보며 이해해보기

B-Tree에 데이터를 삽입하는 과정에서 만약 리프 노드가 루트 노드가 아니라고 한다면
이 과정은 어떻게 보면 노드의 분할과 병합이 일어나는 경우와 그렇지 않은 경우 2가지로 구분해 볼 수도 있다.
그럼 아래에서 이 두가지 케이스에 대해 다루어보자.

[B-Tree 데이터 삽입 과정 되짚어보기]
1. 새로운 데이터를 삽입하기 위한 리프 노드를 탐색한다.
2. 발견된 리프 노드에 새로운 데이터를 추가한다.
3. 노드의 분할과 병합(리프 노드가 루트 노드가 아닐 경우)

• 노드의 분할과 병합이 수행되지 않는 경우
• 노드의 분할과 병합이 수행되는 경우

[설명에 사용될 문자]
M : 하나의 노드가 가질 수 있는 최대 데이터 개수

Case 1. 노드의 분할(Split), 병합(Merge)이 수행되지 않는 경우

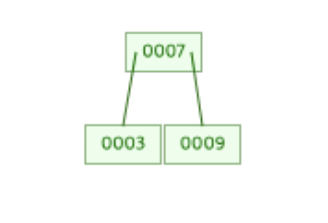
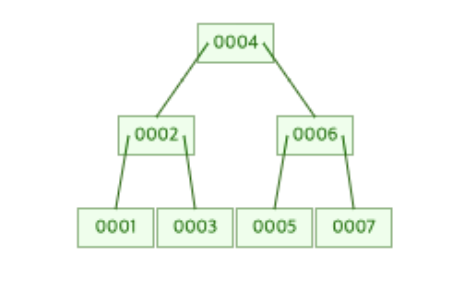
위와 같은 3차 B-Tree가 있다고 해보자.
우리는 이 B-Tree에 8이라는 새로운 값을 삽입하고자 한다.
그럼 가정 처음 해야할 일은 8을 삽입하기 위한 리프 노드를 탐색하는 것이다.
이 경우 8은 루트 노드의 값 7보다는 크기 때문에 루트 노드의 오른쪽 서브 트리에 저장된다.
따라서 8은 [9]가 존재하는 오른쪽 노드에 저장된다.
현재 위의 트리는 3차 B-Tree이다. 그래서 8을 저장한 뒤에도 데이터의 개수가 M보다 작다.
그러므로 8을 추가한 후에 데이터의 삽입 과정이 종료된다.
아래의 그림은 8이 추가된 후의 최종 B-Tree의 모습이다.

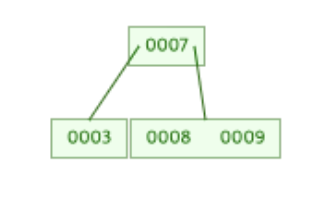
최종 B-Tree의 모습에서 조금 더 살펴보자면 8은 기존에 존재하던 9보다는 값이 작다.
B-Tree의 규칙 중 "노드 안에 존재하는 데이터는 정렬이 되어있어야 한다."라는 규칙이 있었다.
따라서 새롭게 삽입된 8은 9보다 앞에 존재하게 된다.

만약 첫 번째 그림에서 10이라는 데이터를 삽입하게 된다면 결과는 아래와 같을 것이다.

---

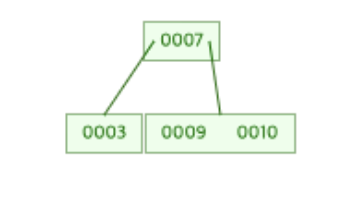
Case 2. 노드의 분할(Split)과 병합(Merge)이 수행되는 경우

우리는 앞서 노드의 분할과 병합이 수행되지 않는 경우에 대해 살펴보았다.
노드의 분할과 병합이 수행되는 경우는 조금 더 세분화해보면 아래와 같이 나누어볼 수 있다.

• Leaf Node만 분할이 일어나는 경우
  • 부모 노드와의 병합이 발생
• Leaf Node와 Branch Node(해당 Leaf Node의 부모 노드)가 함께 분할이 일어나는 경우
  • 리프 노드의 부모 노드와의 병합이 발생
  • 브랜치 노드의 부모 노드와 병합이 발생
• Leaf Node부터 Root Node까지 모두 분할이 일어나는 경우
  • 리프 노드의 부모 노드와 병합이 발생
  • 브랜치 노드의 부모 노드와 병합이 발생
  • 루트 노드의 분할이 발생

여기에서는 Leaf Node의 분할과 병합이 수행되는 과정을 살펴보면서 "노드의 분할 및 병합이 수행되는 경우"에 대해 조금 더 깊게 이해해보자.
왜냐하면 Leaf Node와 Branch Node 의 분할, 병합 과정과 Leaf Node부터 Root Node까지의 분할, 병합 과정은 Leaf Node의 분할, 병합 과정과 모두 동일한 방법으로 이루어지기 때문이다.
(아래 참고에 Leaf Node & Branch Node의 분할, Leaf Node부터 Root Node까지의 분할 과정을 그림으로 나타내었다. 필요하다면 본문의 내용을 이해한 뒤 이를 살펴보면서 천천히 생각해보자!)

자, 그럼 노드의 분할과 병합이 일어나야 하는 경우에 대해 살펴보자.

[설명에 사용될 문자]
M : 하나의 노드가 가질 수 있는 최대 데이터 개수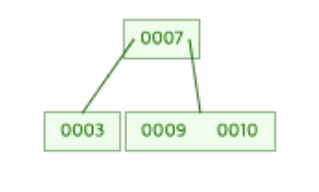

우선 위와 같은 3차 B-Tree가 있고 여기에 8을 새롭게 삽입한다고 해보자.
그럼 먼저 8은 루트 노드의 Key값인 7보다는 크기 때문에 오른쪽 노드에 저장된다.

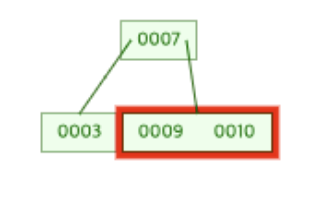
따라서 [9, 10]이 존재하는 노드에 8이 저장된다.
8이 저장된 후의 B-Tree는 아래의 그림과 같은 모습이 된다.
(8은 [9, 10]보다는 작기 때문에 9보다 앞에 존재해야 한다. 즉, 값의 비교를 통해 데이터가 저장되어지며 이를 통해 노드에 존재하는 값이 정렬된 상태를 유지하게 된다.)

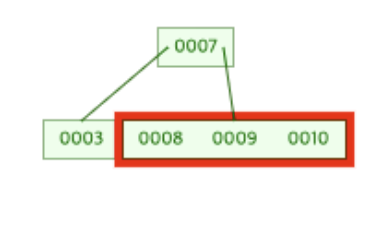
8이 새롭게 저장된 후 [9, 10]이 존재하던 노드는 [8, 9, 10] 총 3개의 데이터를 가지게 되었다.
즉, 노드의 데이터 개수가 M과 같아졌기 때문에 분할이 일어나야한다.
해당 노드가 분할된 모습은 아래와 같다.

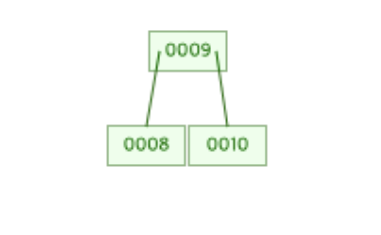
노드를 분할하고 보니 [8, 9, 10]을 가진 노드는 부모 노드([7]을 가진 루트 노드)가 존재했다.
따라서 분할되어 재구성된 서브 트리의 루트 노드 즉, 9는 [7]을 가진 루트 노드와의 병합이 필요하게 된다.
아래의 그림은 병합 과정까지 모두 이루어진 B-Tree의 최종 모습이다.

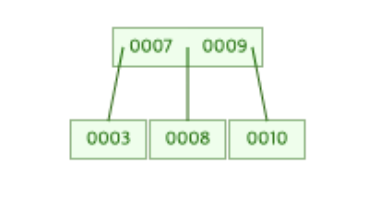
정리해 보자.
8을 새롭게 추가하여 [8, 9, 10]을 가지게 된 전체 트리의 오른쪽 노드가 분할돼 중간 값인 9가 루트 노드가 되고,
8은 루트 노드의 왼쪽 노드로, 10은 루트 노드의 오른쪽 노드로 재구성된 서브 트리의 모습으로 바뀌게 된다.
그리고 [9]를 가진 서브 트리의 루트 노드는 [7]을 가진 전체 트리의 루트 노드와 병합 과정이 이루어지게 되고
그 후 데이터 삽입이 종료된다.

여기서 "데이터 삽입의 과정에서 노드의 분할과 병합이 일어날 수 있다."라는 사실이 중요하다.

왜냐하면 "인덱스 사용시 데이터의 삽입 성능이 저하된다."라는 의미 안에 노드 분할과 병합에 드는 비용이 포함되어지기 때문이다.
물론 리프 노드의 탐색과 노드에 존재하는 데이터의 정렬을 위한 비용도 포함될 것이다.(Update, Delete도 마찬가지이지만 해당 내용이 데이터 삽입에 대한 내용이기에 삽입만을 언급했습니다.)

노드의 분할과 병합에서 조금 더 생각해 보아야 할 것은 최악의 경우 Leaf Node뿐만 아니라 Branch Node를 거쳐 Root Node까지 모두 분할의 과정을 거쳐야 하는 시기가 찾아온다는 것이다.
그리고 이와 같이 만약 Leaf Node부터 Root Node까지 모두 분할이 되어야 한다면, 이는 곧 "데이터 삽입에 드는 시간이 더욱 오래 걸린다."라는 것을 의미하게 된다.

이로써 우리는 위의 과정을 통해 인덱스를 사용할 때, 왜 데이터 삽입의 성능이 저하되는지 이해할 수 있게 되었다!

---

정리

• B-Tree의 데이터 삽입은 상향식으로 진행된다. 즉, B-Tree의 데이터 삽입은 항상 리프 노드(Leaf Node)에서부터 시작된다는 것이다.

• B-Tree의 데이터 삽입 과정

  • 새로운 데이터를 삽입하기 위한 리프 노드를 탐색한다.
  • 리프 노드 발견시 새로운 데이터를 추가한다
  • 새로운 데이터 추가 후 필요하다면 노드의 분할(Split)과 병합(Merge)이 수행된다.

• 노드의 분할(Split)

  • 특정 리프 노드의 현재 데이터 수가 노드가 가질 수 있는 최대 데이터 개수가 될 때, 해당 리프 노드의 데이터들 중 중간 값을 기준으로 해당 값보다 작은 값을 왼쪽 노드로, 큰 값을 오른쪽 노드로 분할하여 재구성하는 과정을 의미한다.

• 노드의 병합(Merge)

  • 만약 분할이 일어나는 노드가 루트 노드가 아닐 경우, 해당 노드는 반드시 리프 노드이다.
    (사실 트리에 루트 노드만 존재할 경우 루트 노드는 루트 노드이면서 리프 노드이다.)
  • 따라서 해당 노드는 반드시 부모 노드를 가지게 된다.
  • 그러므로 리프 노드가 분할의 과정을 거치면서 재구성된 해당 서브 트리의 루트 노드는
    기존 자신의 부모 노드와 합쳐지는 과정을 거치게 되는데 이를 노드의 병합이라고 한다.

• 노드의 분할, 병합 수행 케이스

  • 노드의 분할(Split)과 병합(Merge)은 모두 수행될 수도 있다.
  • 노드의 분할(Split)과 병합(Merge)은 모두 수행되지 않을 수도 있다.
  • 경우에 따라 분할(Split)만 수행되어질 수도 있다.
    • 노드의 병합(Merge)은 분할 과정 이후에 조건에 따라 수행되는 것이므로 병합 과정만 단독으로 수행되는 경우는 존재하지 않는다.
    • 리프 노드가 루트 노드일 경우 노드의 분할이 이루어지더라도 병합은 수행되지 않는다.(전체 트리에서 루트 노드는 부모 노드가 없다.)
    • 리프 노드가 루트 노드가 아닐 경우 분할이 수행된 후에 부모 노드와 병합되는 과정이 발생한다.

• 데이터가 삽입되는 리프 노드가 루트 노드가 아닐 경우 노드의 분할과 병합은 크게 2가지 케이스로 나누어볼 수 있다.

  • 노드의 분할과 병합이 일어나지 않는 경우
    • 새로운 데이터를 저장하기 위한 노드의 탐색 비용 발생.
    • 노드 안에 존재하는 데이터 정렬을 위한 비용이 발생.
  • 노드의 분할과 병합이 일어나는 경우
    • 새로운 데이터를 저장하기 위한 노드의 탐색 비용 발생.
    • 노드 발견 후 3가지 케이스로 나누어 생각해볼 수 있다.
      • 데이터가 추가된 리프 노드만 분할, 병합 과정이 수행되는 경우
      • 데이터가 추가된 리프 노드와 부모 노드(Branch Node)가 함께 분할 및 병합이 수행되는 경우
      • 데이터가 추가된 리프 노드에서 부터 부모 노드(Branch Node)를 거쳐 Root Node까지 모든 노드가 분할, 병합 과정이 수행되는 경우

• 인덱스 사용시 "데이터 삽입의 성능이 저하될 수 있다."는 의미는 아래와 같은 비용이 발생하기 때문이다.

  • 새로운 데이터를 저장하기 위한 노드의 탐색 비용 발생.
  • 데이터 추가 시 데이터 정렬을 위한 비용의 발생. (값의 비교)
  • 데이터 추가 시 노드의 분할 및 병합이 일어나는 과정에서 발생하는 비용 발생.

---

참고

1. 데이터가 추가된 Leaf Node와 부모 노드(Branch Node)가 함께 분할, 병합이 수행되는 경우

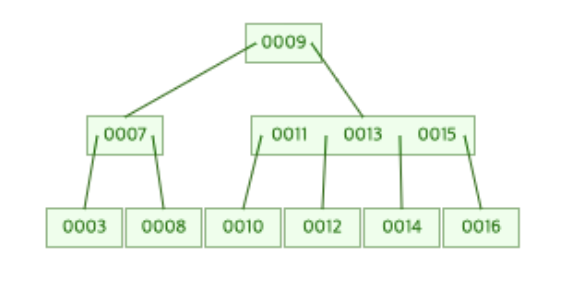
아래의 B-Tree는 3차 B-Tree 이다. 즉, 하나의 노드가 가질 수 있는 최대 데이터의 개수는 3개라는 의미이다.
여기에 16을 새롭게 추가해보겠다.

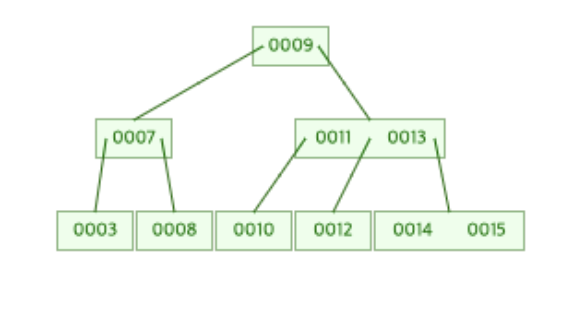
16추가!

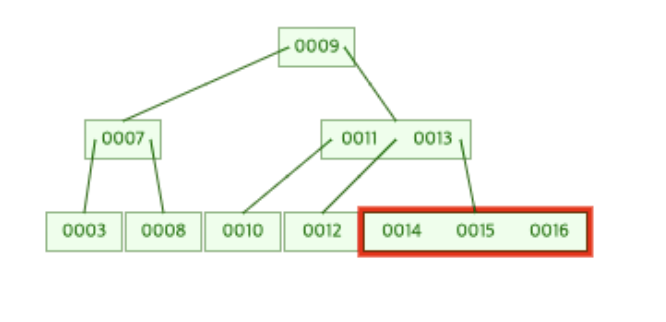
16을 새롭게 추가함으로써 [14, 15]가 존재하던 맨 오른쪽 Leaf Node에 16이 추가된 후 분할이 일어나게 된다.

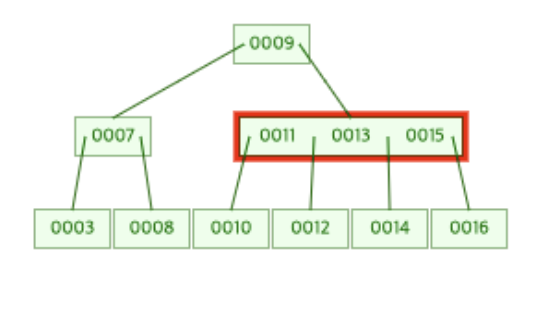
이때 분할이 일어나면서 15가 부모 노드로 올라가게 되는데(병합), 15가 추가되면서 부모 노드의 데이터 개수도 [11, 13, 15] 3개가 되어지고 이는 하나의 노드가 가질 수 있는 최대 데이터의 개수가 되기때문에 또 다시 분할이 이루어지게 된다.

최종적으로 16이 추가된 후 B-Tree의 모습은 아래와 같이 바뀌게 된다.

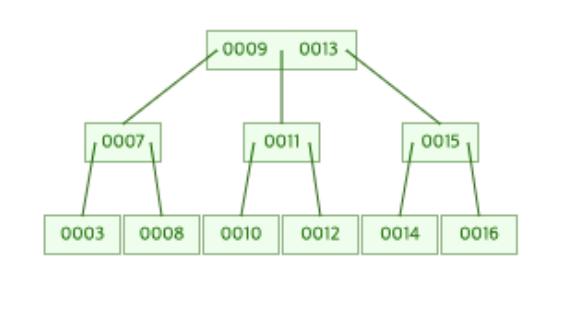
위의 그림에서 알 수 있듯 [13]을 가진 노드가 루트 노드와 병합되었다.

2. 데이터가 추가된 Leaf Node에서부터 Root Node까지 모두 분할 및 병합이 수행되는 경우

아래의 B-Tree는 3차 B-Tree 이다. 즉, 하나의 노드가 가질 수 있는 최대 데이터의 개수는 3개라는 의미이다.
우리는 여기에 20을 새롭게 추가해볼 것이다.

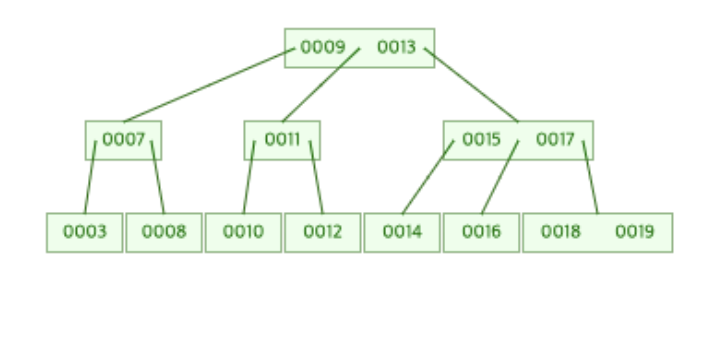
20추가!

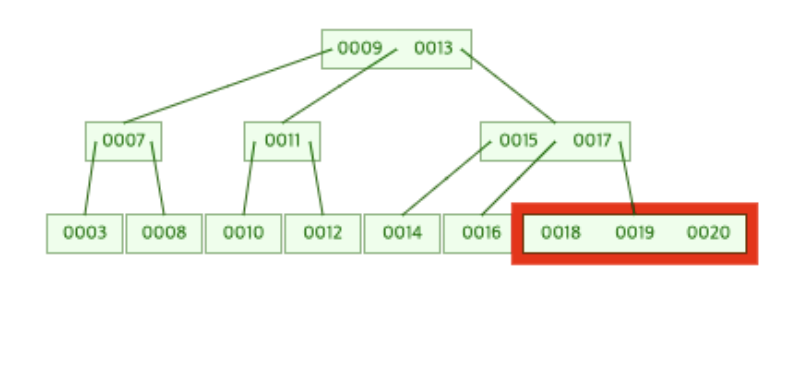
20을 추가함으로써 [18, 19]가 존재하는 맨 오른쪽 Leaf Node의 데이터 개수가 3개가 되었다. 따라서 노드의 분할 과정이 일어나게 된다.

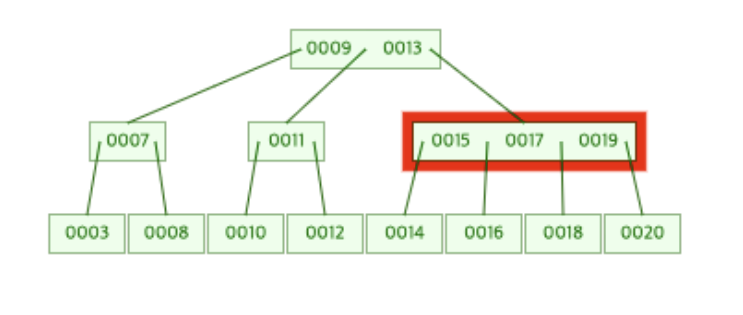
Leaf Node가 분할이 되면서 19가 부모 노드로 올라오게 되었다.(병합)
그런데 이때 [15, 17]이 존재하던 부모 노드도 19가 새롭게 추가되면서 데이터 개수가 3개가 되어 분할이 일어나게 된다.

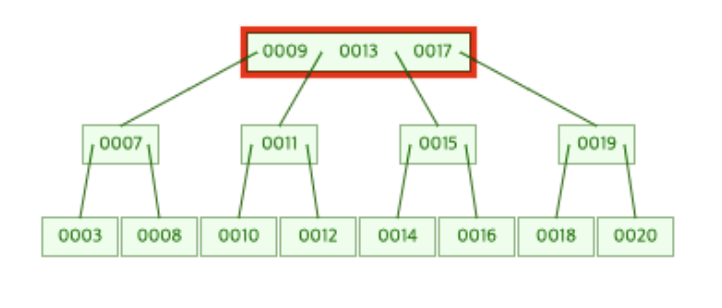
[15, 17, 19]가 존재하게 된 Branch Node가 분할되면서 17이 루트 노드로 올라오게 되었다.(병합)
그런데 17이 새롭게 추가되면서 루트 노드의 개수도 3개가 되어 분할이 일어나게 된다.

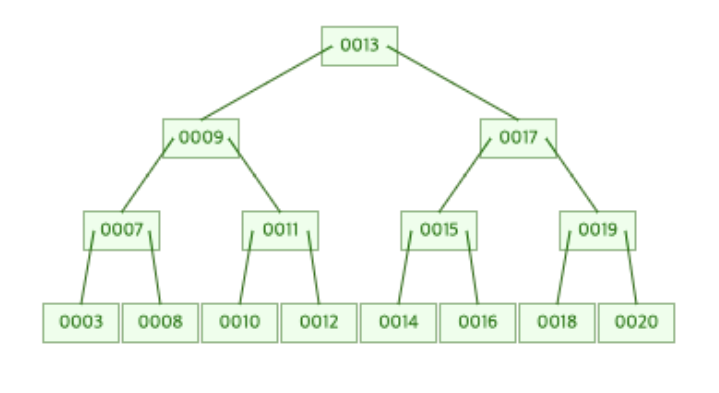
루트 노드가 분할이 된 후 B-Tree의 최종 모습은 위의 그림과 같다.
결국 Root Node가 분할되면서 13을 저장하는 새로운 Root Node가 생기게 되고 9는 Root Node의 왼쪽으로, 17은 Root Node의 오른쪽으로 나뉘어지게 된다.
20이라는 수 하나 추가하기 위해 총 3번의 페이지 분할이 일어난 것이다..