[Ensemble] Bagging

Ensemble의 diversity는 data diversity, model diversity 두가지가 있는데, bagging은 data diversity에 관한 것이다.

K-fold data split

K-fold 교차 검증은 단일 데이터 분할보다 신뢰성이 높고, 모델의 일반화 성능을 더 정확하게 평가할 수 있도록 도와줍니다. 이를 통해 모델이 특정 데이터에 과적합되지 않고 다양한 데이터에 대해 효과적으로 작동하는지를 확인할 수 있다.
K-fold 데이터 분할은 기계 학습에서 모델의 성능을 평가하고 향상시키기 위해 사용된다. 여러 번의 실험을 수행하고 결과를 평균 내어 모델의 성능을 더 신뢰할 수 있게 평가할 수 있다.

1. 데이터 세트를 무작위로 섞습니다.
2. 전체 데이터를 균등한 크기의 K개 부분(또는 폴드)으로 나눕니다.
3. K번의 반복 동안 각각의 폴드를 검증 데이터로 사용하고, 나머지 K-1개 폴드를 훈련 데이터로 사용하여 모델을 훈련합니다.
4. 각 반복에서 얻은 성능 지표(예: 정확도, 정밀도, 재현율 등)를 기록합니다.
5. K번의 반복이 완료된 후, 성능 지표의 평균을 계산하여 모델의 최종 성능을 평가합니다.

• 단점
  k-1개를 학습하다보니 손실이 일어남
  무작정 많이 만들고 쪼개는데 한계가 있음
  => bootstrap aggregating: bagging

bootstrap aggregating: bagging

여러개의 bootstrap 자료를 생성하고 각 자료를 모델링한 후 결합하여 최종 예측 모델을 산출한다.
bootstrap 자료란 raw data로부터 복원 임의 추출한 크기가 동일한 여러개의 표본자료이다.
대표적으로 랜덤 포레스트 알고리즘을 사용하여 overfitting 방지에 효과적이며 수행속도가 빠르다는 장점이 있다.

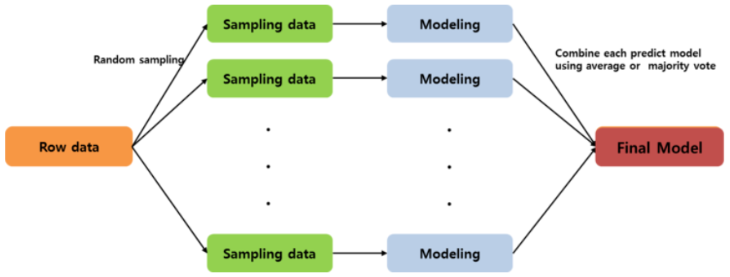
Main idea

sampling with replacement: 복원추출 
- 똑같은 데이터가 여러번 선택될수도, 아예 선택이 안될수도 있다.
- 원하는 만큼 bootstap 추출 가능
- 데이터가 가진 분포를 바꿈: 왜곡을 통해 종속적인 데이터가 만들어질 수 있는 위험을 줄인다.

Bagging with Decision Tree

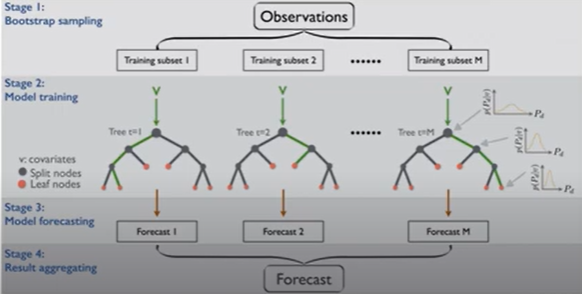
stage1에서 복원추출 데이터 사용
stage 2에 any supervised learning algorithm 써도 상관없음

Result Aggregating

- Classification problem
![](https://velog.velcdn.com/images/yomilimi/post/a2c07a1f-f375-4305-a984-629bf0252f45/image.png)
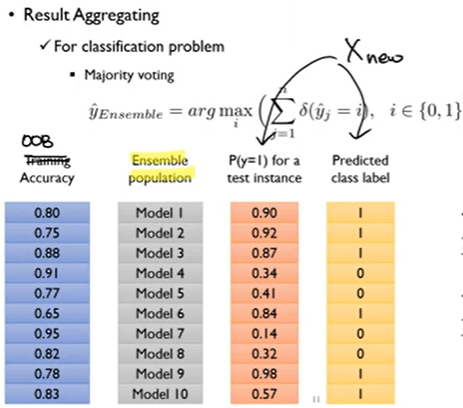
1. majority voting
predictied class label만 사용해서 결과 구한다.
![](https://velog.velcdn.com/images/yomilimi/post/7db5ad4a-70ca-484b-ab51-c5aae8a95f84/image.png)
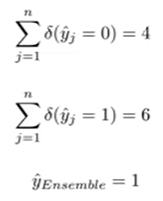
2. weighted voting
가중치 준다.
![](https://velog.velcdn.com/images/yomilimi/post/bdd05fd2-0990-41b6-bcd3-f73e64629364/image.png)
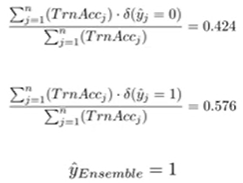
- Regression problem: 단순 평균

Random Forests

specialized bagging for decision tree algorithms: tree가 여러 개 모여서 forest가 됨

Two ways to increase the diversity of ensemble
1. bagging
2. randomly chosen predictor variables

Bagging

• sampling with replacement
  

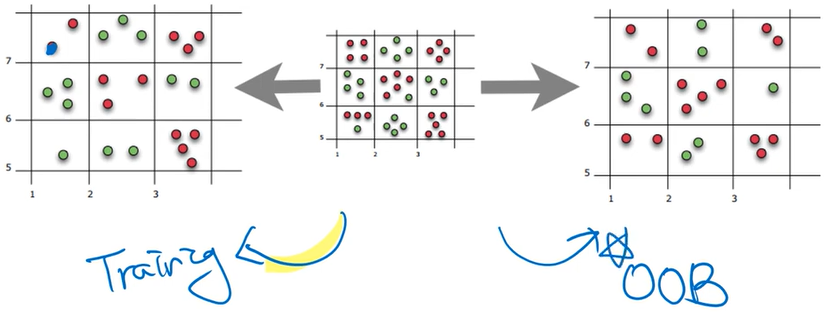
• randomly selected variable
  
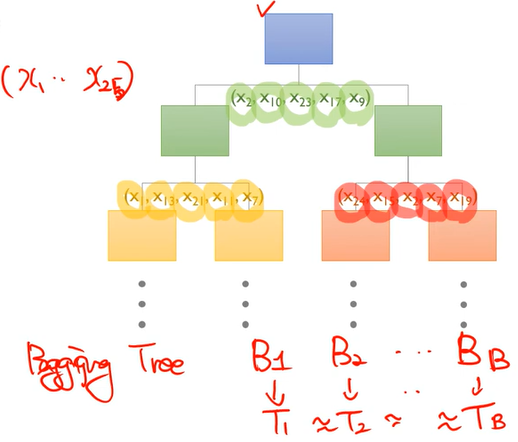
  변수를 선택적으로 사용하자
  B 각각 성능이 떨어져도 이들을 합치면 성능이 올라간다.

Generalization error

개별 모델들의 성능이 좋고, 모델간의 연관성이 없을수록 Generalization error가 낮아진다.

Variable Importance

step1: compute the OOB error for the original dataset(ei)
step2: compute the OOB error for the dataset in which the variable xi is permutes(pi)
step3: compute the variable importance based on the mean and standard deviation of(pi-ei) over all trees in the population: pi-ei가 클수록 중요함


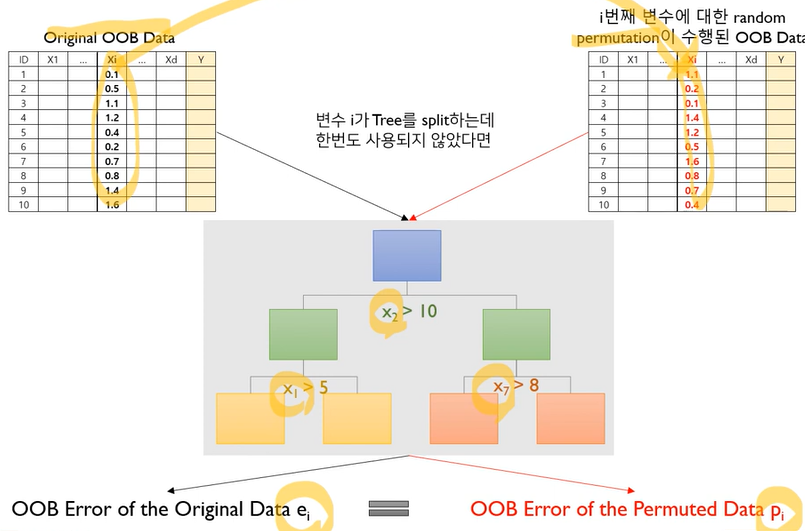
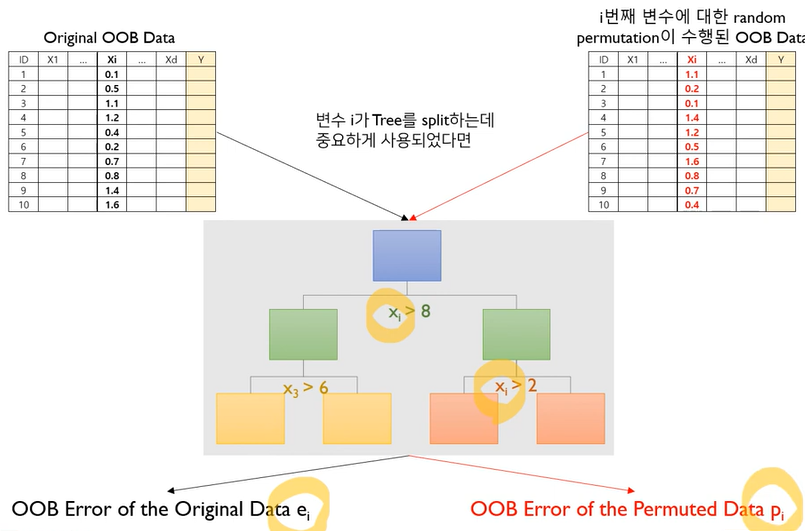
랜덤 포레스트에서 변수의 중요도가 높다면
1) Random permutation 전-후의 OOB Error차이가 크게 나타나야 하며,
2) 앙상블 개별적인 트리마다 그 차이의 편차가 적어야 함: 일관성 있게 중요해야 됨