출처 : 자료구조 힙 (heap) make_heap 연산
힙
정의
힙 성질을 만족하는 이진 트리
힙 성질
- 힙 모양 성질
이진 트리를 배열 형태로 저장하며 k 번째 부모 노드의 자식 노드는 () 에 존재함
그 이유에 대한 설명은 여기에- 힙 성질
부모 노드의 값이 자신의 자식 노드에 비해서 무조건 크거나 같아야 한다.
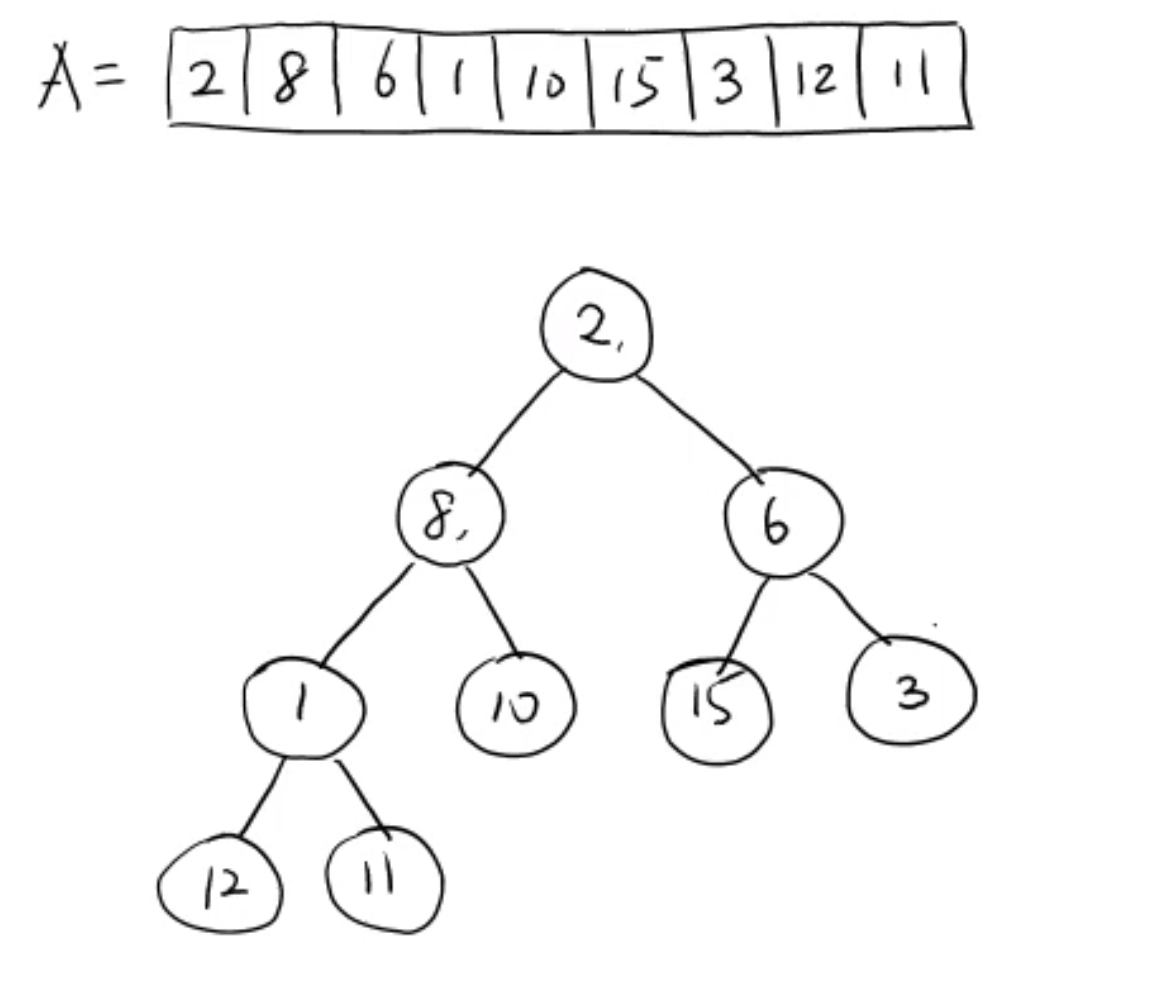
다음처럼 힙 성질을 만족하지 않는 이진 트리가 존재한다고 했을 때 힙 성질을 만족하도록 배열을 재배치 하여 힙으로 만들자
힙으로 만드는 단계를 이라고 한다.
makeheap
makeheap 을 할 때는 부모 노드와 자식 노드를 교체하는 heapify-down 을 거치게 된다.
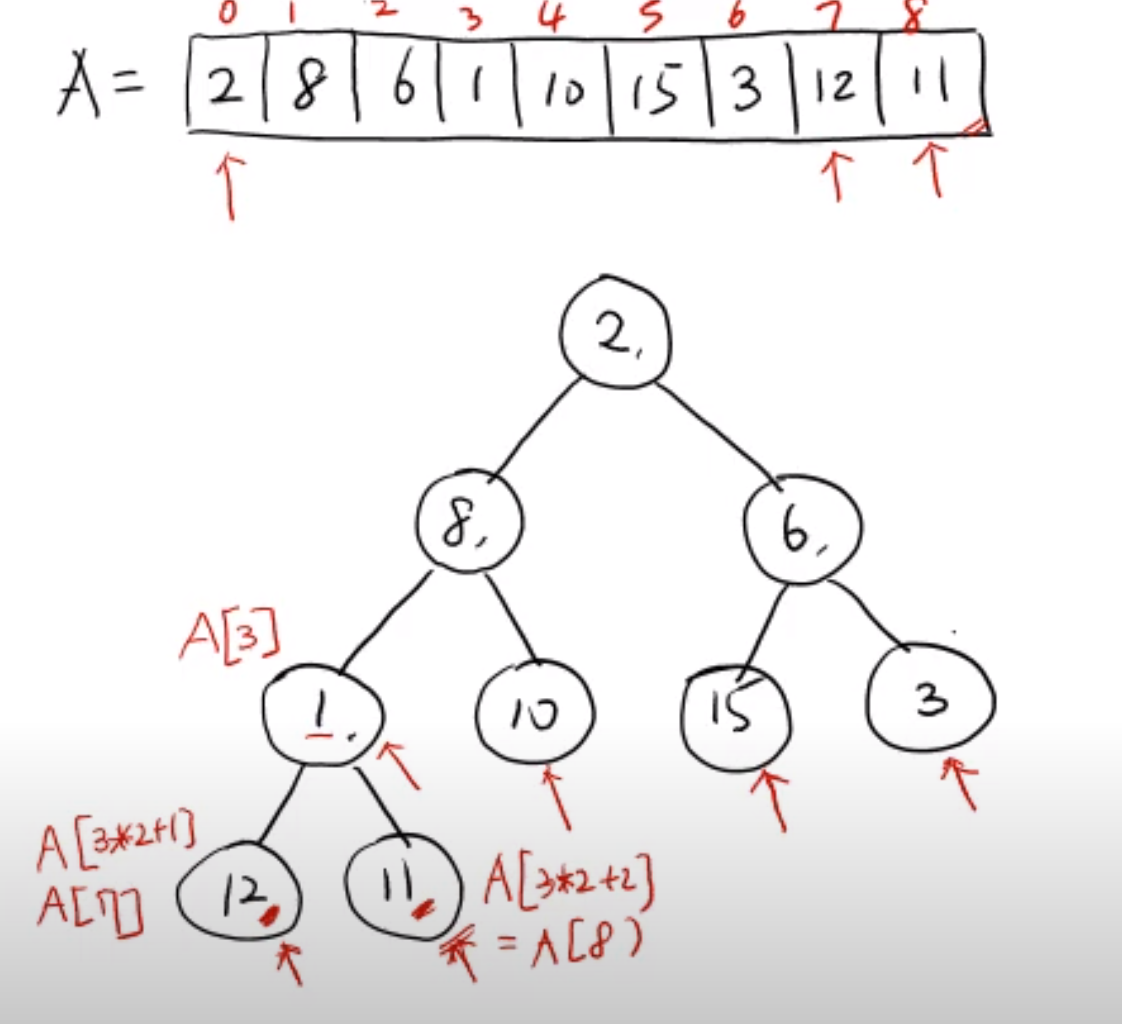
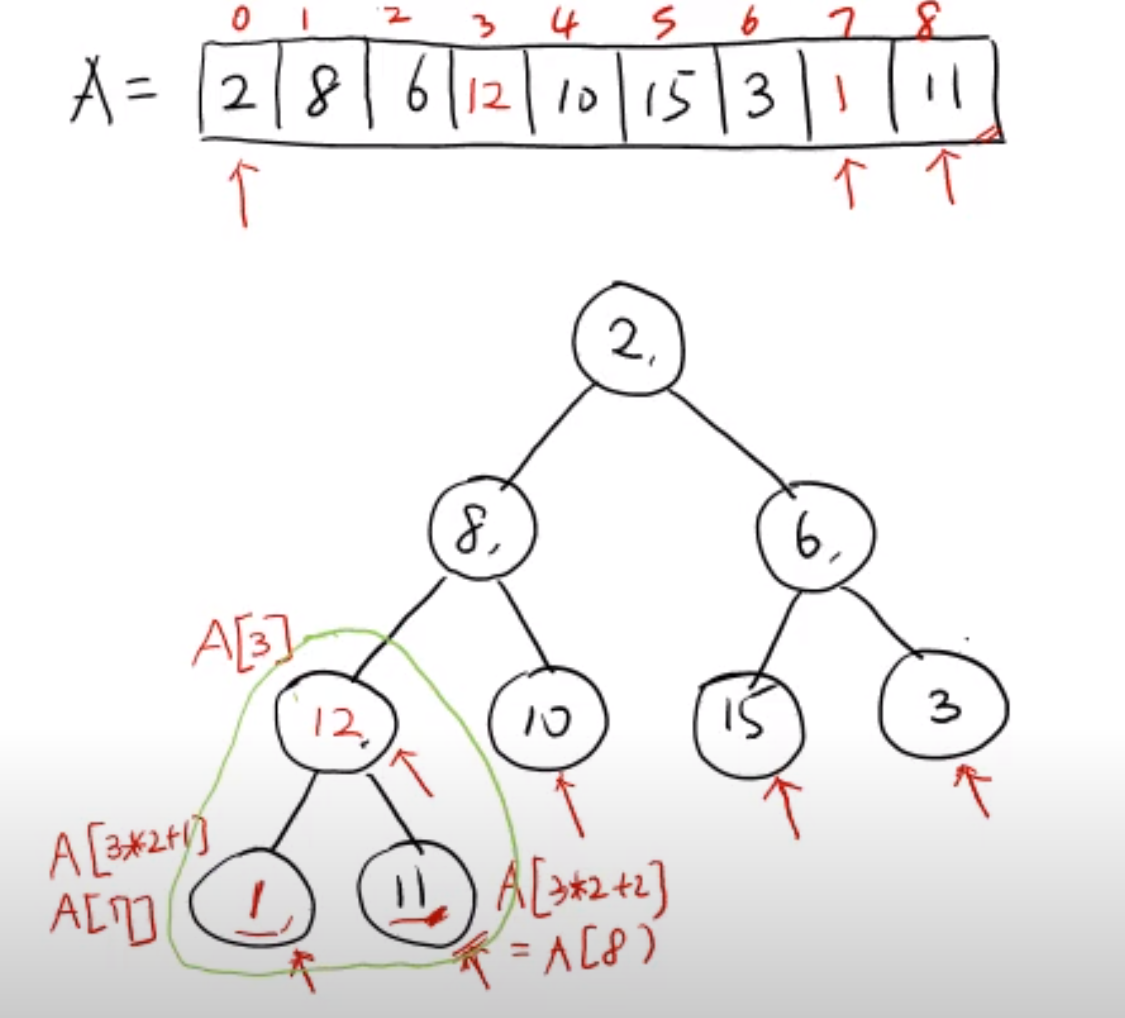
makeheap 을 코드를 통해 이해해보자
class Heap:
def __init__(self , L = []):
self.A = L
self.make_heap()
def __str__(self):
return str(self.A)
def heapify_down(self,k,n):
'''
n = 힙의 전체 노드수
A[k] 를 힙 성질을 만족하는 위치로 내려가면서 재배치
'''
while 2 * k + 1 < n:
L,R = 2 * k + 1 , 2 * k + 2
if self.A[L] > self.A[k]:
m = L
else:
m = k
if R < n and self.A[R] > self.A[m]:
m = R
if m != k:
self.A[k] , self.A[m] = self.A[m] , self.A[k]
k = m
else:
break
def make_heap(self):
n = len(self.A)
for k in range(n-1 , -1, -1):
self.heapify_down(k,n)맨 처음 힙 모양의 배열을 받은 후 make_heap() 이라는 함수를 호출하여 바로 힙 성질을 만족하도록 정렬해주는 모습을 def __init__() 에서 볼 수 있다.
그러면 make_heap() 은 뭔가 하고 보니
make_heap() 은 배열의 마지막부터 시작해서 맨 앞까지 돌아가면서 heapify_down 을 시행하는 모습을 볼 수 있으며 파라미터로는 현재 인덱스와 배열의 길이를 받고 있다.
그러면 heapify_down 을 이해하면 될 것이다.
heapify_down
함수의 일부분을 뜯어가면서 이해해보자
def heapify_down(self,k,n):
'''
n = 힙의 전체 노드수
A[k] 를 힙 성질을 만족하는 위치로 내려가면서 재배치
'''
while 2 * k + 1 < n:
L,R = 2 * k + 1 , 2 * k + 2
if self.A[L] > self.A[k]:
m = L
else:
m = k
if R < n and self.A[R] > self.A[m]:
m = R
...A: 힙 모양으로 받은 배열k: 배열에서 위치가 k인 부모 노드L,R:k의 왼쪽 , 오른쪽 자식 노드 (힙 모양을 만족하는 배열에서는 k 의 자식 노드는 )m:A[k],A[L],A[R]중 가장 큰 값에 대한 인덱스
여기까지 코드를 보면 K 번째 위치에 존재하는 부모 노드와 왼쪽, 오른쪽 자식 노드의 값을 비교하여 가장 큰 값의 인덱스를 m 이라는 변수에 저장한다.
if m != k:
self.A[k] , self.A[m] = self.A[m] , self.A[k]
k = m
else:
break이후 m != k 를 통해서 만약 부모노드인 A[k] 가 자식 노드들보다 값이 작다면
self.A[k] , self.A[m] = self.A[m] , self.A[k]
k = m 를 통해서 부모노드와 자식 노드 간의 값을 바꿔주는 모습을 볼 수 있다.
그리고 k = m 으로 설정해준다. (부모노드였던 A[k] 가 A[m]이 되었으니까)
만약 부모노드인 A[k] 가 자식 노드들보다 값이 크다는 것은 (m == k라면) 조그만 이진 트리 A[k] , A[L] , A [R] 이 힙 성질을 만족한다는 뜻이니 반복문을 멈추게 되어 있다.
만약 m != k 라서 k = m 이 실행 된 채로 첫 번째 반복이 끝났다고 가정해보자
while 문이 모두 끝났다면 다시 조건을 확인 할 것이다.
while 2 * k + 1 < n:로 확인하게 되는데 이 말은 뭐냐면 이미 과거의 k 와 m은 한 번 바뀐 상태이다.
그러니 현재의 while 문은 현재 위치가 바뀐 과거 k 에 대해서 탐색을 다시 하게 된다.
makeheap
def make_heap(self):
n = len(self.A)
for k in range(n-1 , -1, -1):
self.heapify_down(k,n)결국 meakheap 함수를 살펴보면 leaf node 부터 확인하면서 heapify_down 을 살피고 있다.
그럼 만약 for 문이 진행되면서 맨 첫 ! root node 에서 self.heapify_down 이 진행된다고 생각해보자
그리고 root node 에 있던 놈이 알고보니 제~일 마지막 leaf node 에 정렬 되어야 한다는 놈이라고 가정해보자
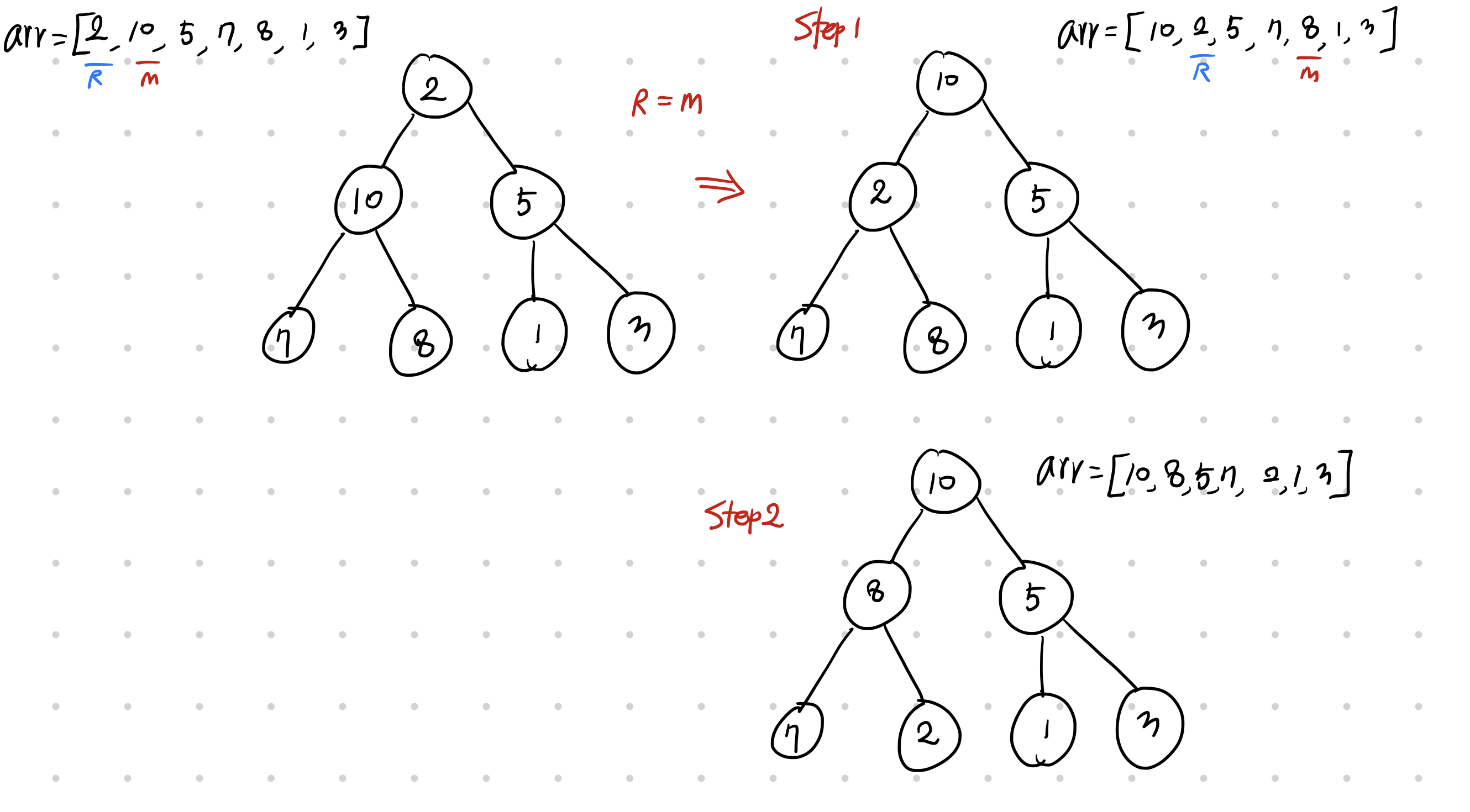
heapify_down 에서 마지막에 k = m 하고 바꿔주기 때문에 반복문이 진행되면서 가장 높은 level 에 있는 노드가 leaf node에 가야 할 때도 무리 없이 변경이 되는 모습을 볼 수 있다.
시간 복잡도는 어떻게 될까 ?
make_heap 을 보면 n 개의 배열에 대해서 heapify_down 을 진행하니
heapify_down 의 시간 복잡도를 라고 하였을 때
걸리는 시간 복잡도는 임을 알 수 있다.
그러면 heapify_down 의 시간 복잡도는 어떻게 될까 ?
heapify_down 의 시간 복잡도
def heapify_down(self,k,n):
'''
n = 힙의 전체 노드수
A[k] 를 힙 성질을 만족하는 위치로 내려가면서 재배치
'''
while 2 * k + 1 < n:
L,R = 2 * k + 1 , 2 * k + 2
if self.A[L] > self.A[k]:
m = L
else:
m = k
if R < n and self.A[R] > self.A[m]:
m = R
if m != k:
self.A[k] , self.A[m] = self.A[m] , self.A[k]
k = m
else:
break코드에서 배열에서 인덱스로 조회하거나 값을 변경, 비교하는 것은 모두 상수 시간안에 해결이 가능하다.
그럼 최악으로 while 문이 계속 진행되는 경우는 k 노드가 leaf node 까지 가는 경우일 것이다.
그렇다면 while 문은 heap 의 높이만큼 진행이 될 것이다.
heap의 높이는 어떻게 될까 ?
우선 배열에는 개의 노드들이 존재하며 높이를 라고 해보자
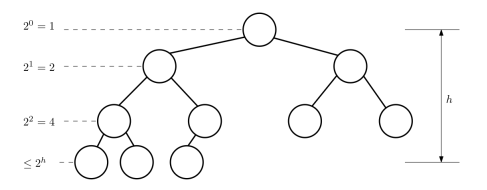
노드 개수 은 높이 에 따라 2의 배수만큼 증가하기 때문에 높이 는 보다 작거나 같을 수 밖에 없다.
그러니 heapify_down 의 시간 복잡도는 이다.
그러면 개의 배열에 대해서 만큼 반복하니
meakheap 의 시간 복잡도는 이다.
