11. Ray Tracing

Ray Tracing은 물리에서는,
파동이나 입자가 굴절율 / 흡수율이 변하는 매질을 통과할 때 그 경로를 계산하는 방식입니다.

근데, CG에선,
Simple (Whitted) Ray Tracing을 의미하는데,
재귀적으로 전반사와 굴절을 고려하는 것을 의미합니다.

Global Illumination을 적용하기 전에 기초적으로 가져야 할 Step이 (Whitted) Ray Tracing입니다.

Approximate이지만, quality면에서 pipeline approach보다 좋습니다.
Raster Pipeline에선 삼각형같은 polygonal mesh만 썼는데,
analytical sphere나 surface같은 implicit representation도 사용합니다.

Ray Tracing Algorithm

Forward와 Backward RT로 나눕니다.

Forward Ray Tracing은

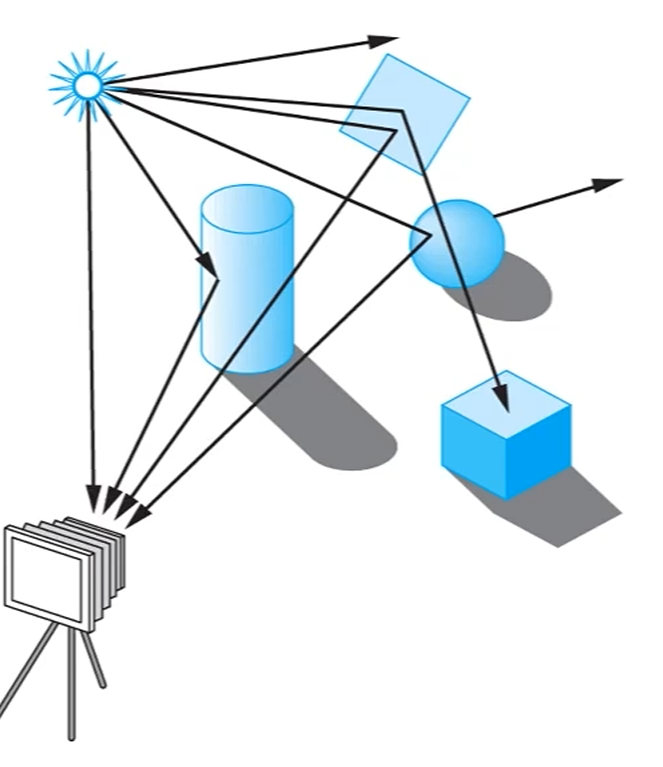
이렇게, 점형 light source에서 나온 ray들이 반사되고, 흡수되고, 어쩌고 해서 돌아오는 빛을 카메라에 담는 것을 Forward Ray Tracing이라고 하구요.

반대방향은 Backward Ray Tracing, 또는 Ray Casting이라고 합니다.

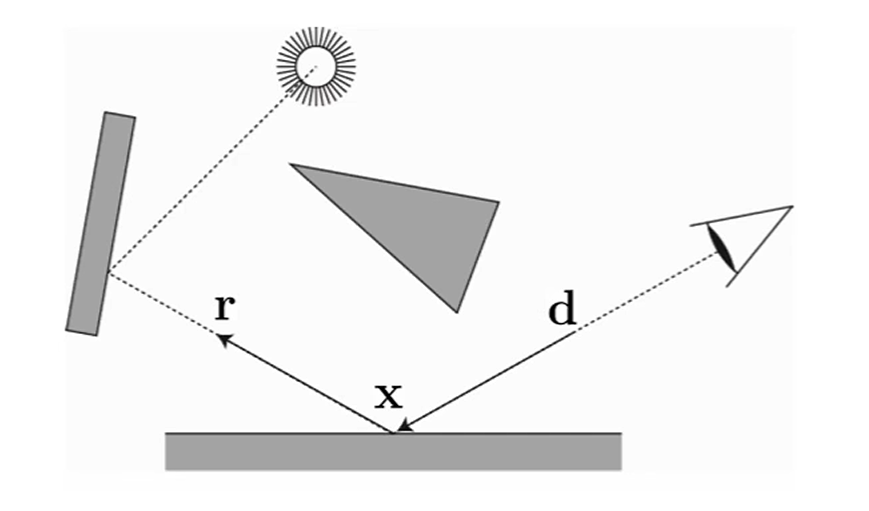
Backward Ray Tracing

카메라 에서 빛을 쏩니다.

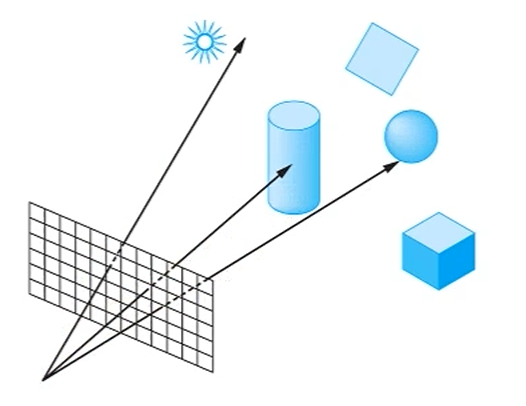
최종적으론 그 ray가 반사되고 투과되고 해서 광원 방향으로 가야 합니다.

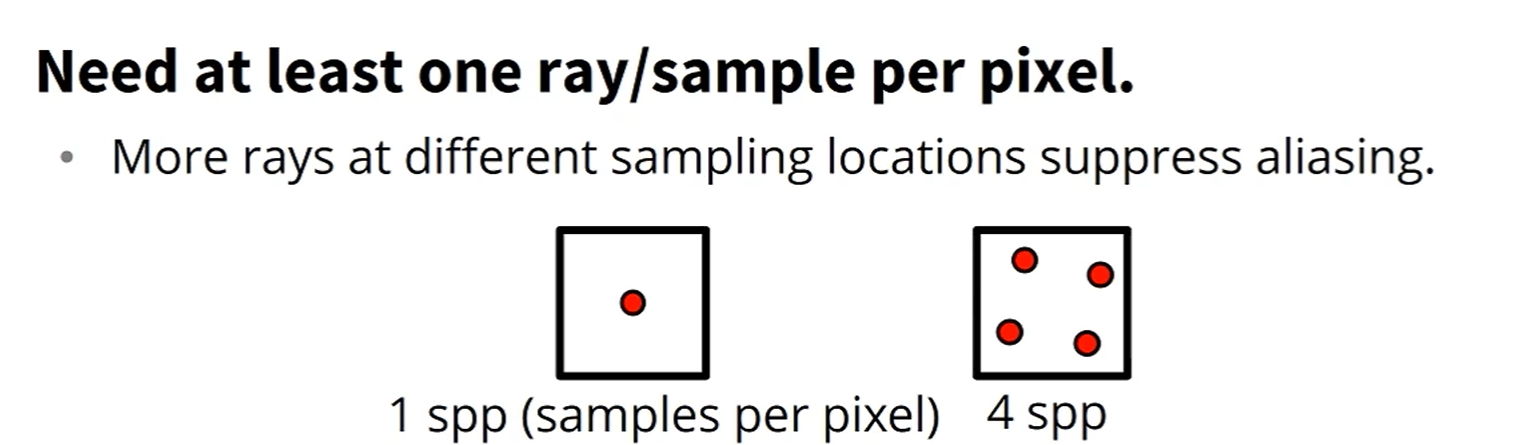
한 픽셀 당 ray를 최소 1개는 쏴야 하구요, (1spp)
많이 쏘고 그것의 평균을 낼 수록 정확한 결과가 나옵니다.

Reflection and Refraction

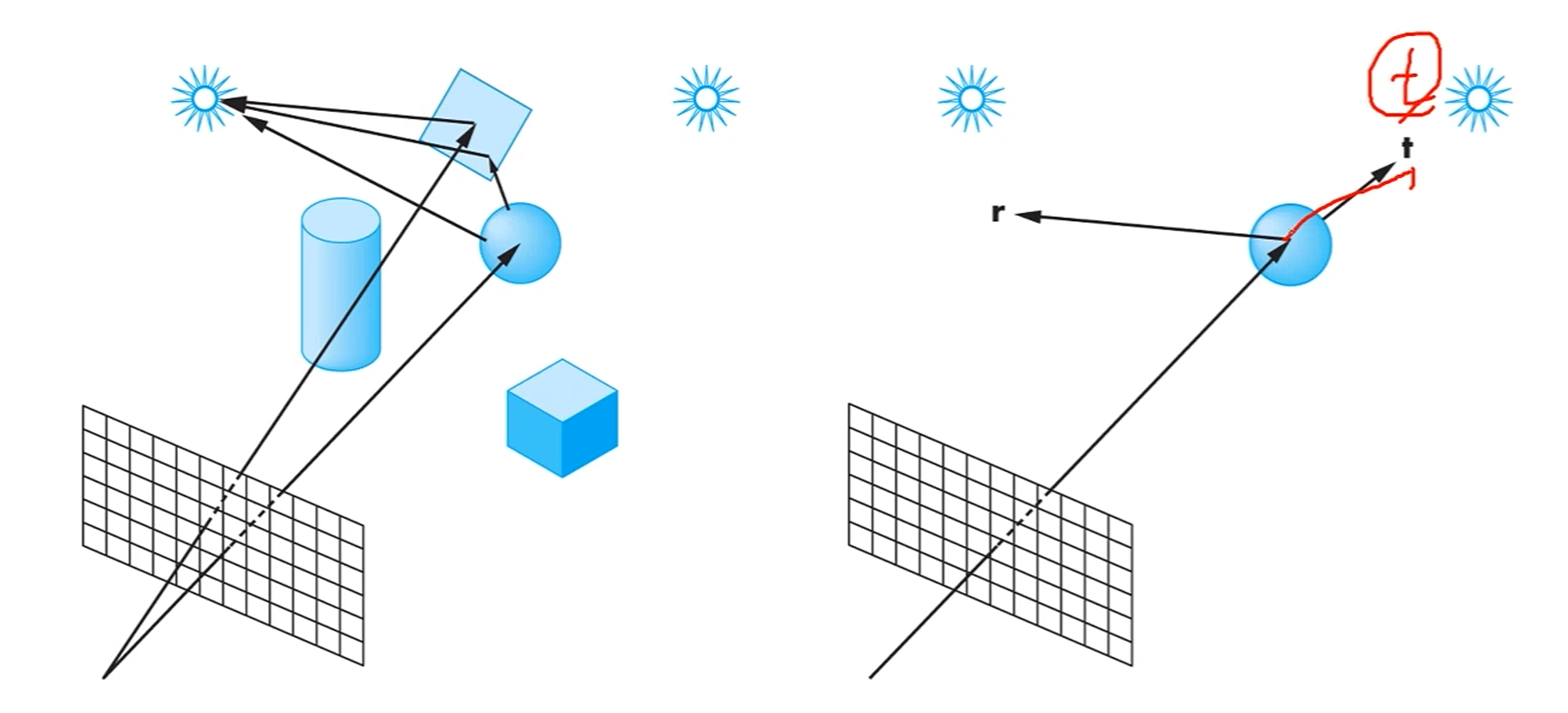
Reflection은 반사고, Refraction(transmission)은 굴절입니다.
Simple Ray Tracing에선 전반사만 구현하는데,

조금 현실적으로 가려면 굴절도 구현되어야 합니다.

Ray Tree

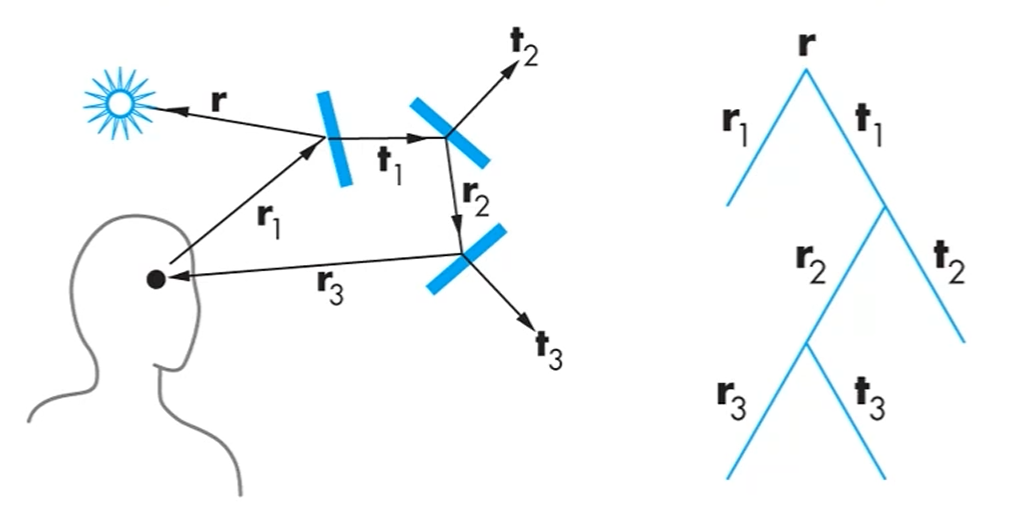
각 object에 대해 반사되는 빛과 굴절되는 빛이 있겠죠?

그리고 각 반사광과 굴절광이 다른 object에 붙으며 또 반사되고 굴절될 수 있겠죠?

반사에서 전반사광만 생각하기로 했으니, Simple Binary Tree로 Ray Tree를 만들 수 있습니다.

Reflection

Phong model에서 다뤘었습니다.

$r = d - 2(d \cdot n)n$으로 구현합니다.

Refraction

빛이 굴절되는 현상입니다.
Snell's Law를 따르면 계산할 수 있습니다.
빛이 Denser Medium에서 더 느리게 이동함을 고려합니다.

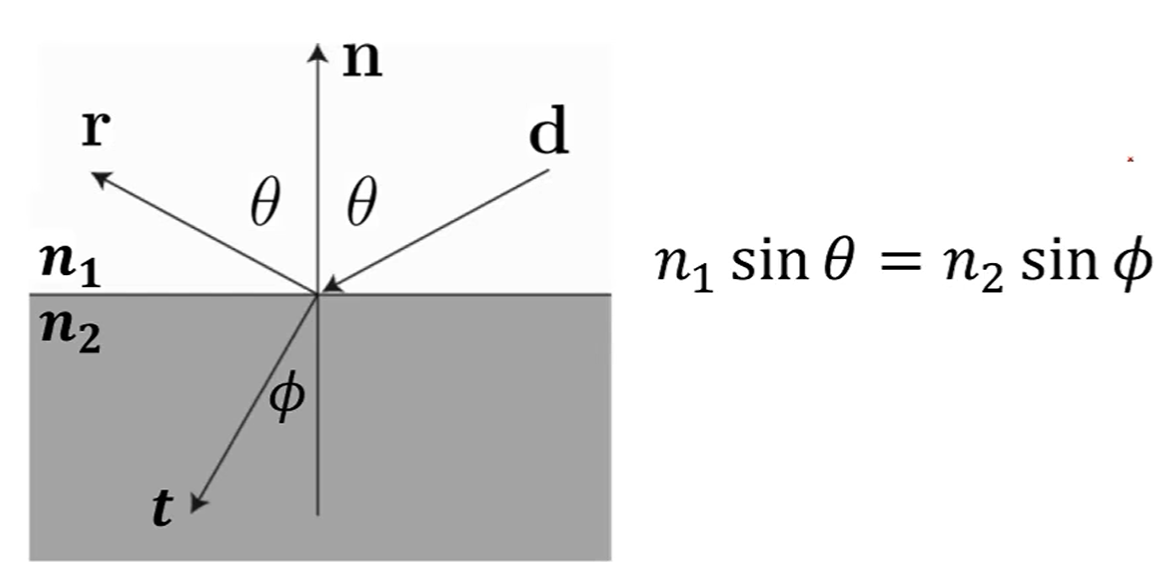
이 때 refractive indice $n_1, n_2$는 굴절율이고, 진공에선 1입니다.

Ray Tracing Pseudocode

각 pixel에 대해 primary ray를 만들고,
primary ray를 trace해서, (0은 depth입니다)
ray tracing tree를 따라 가서 color를 구해낸 후 그 c를 pixel에 박아넣습니다.

Primary Ray

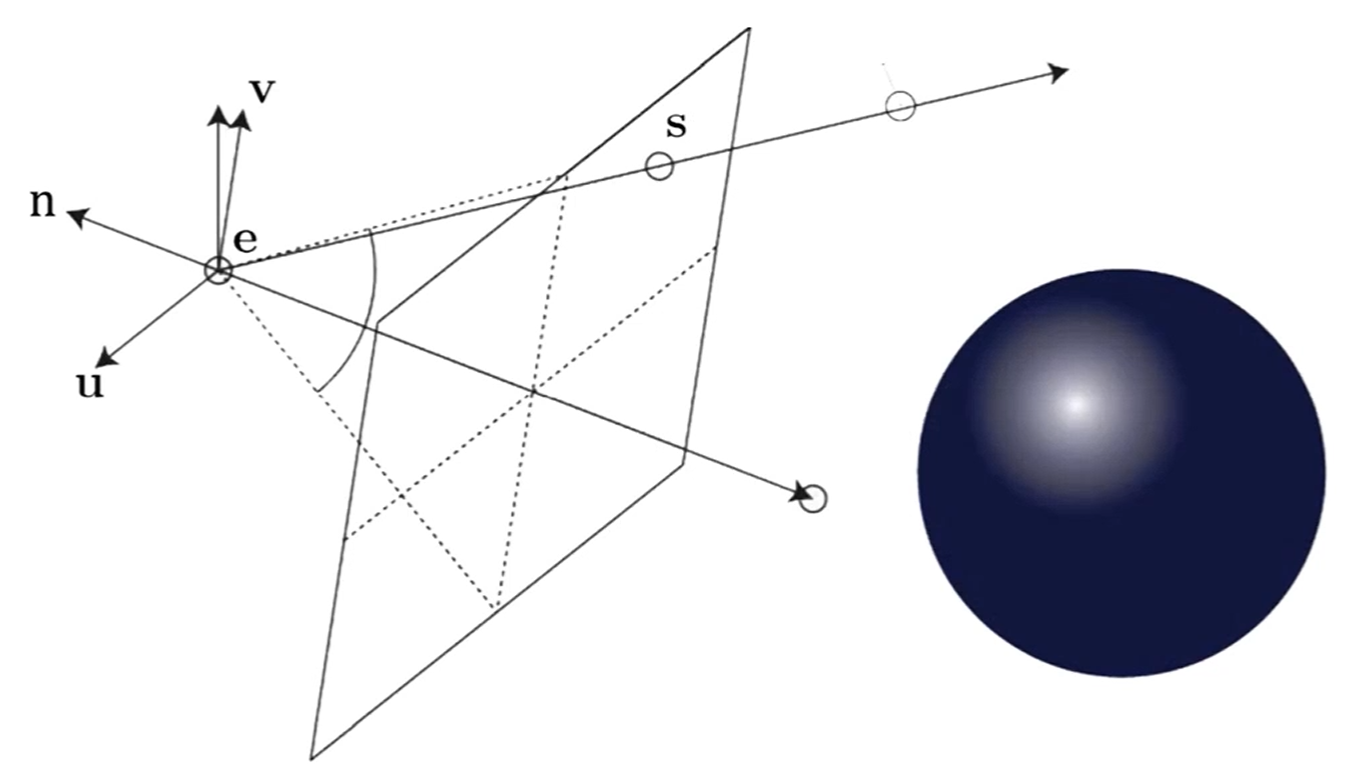
다음과 같은 상황일 때, 이미지 평면에 투영되는 위치 $s$로의 ray 식은
$p(t) = e + t(s-e)$로 쓸 수 있죠.

primary ray는 camera frame에서 나오지만,
그걸 world frame으로 바꿔줘야 합니다.

$e$는 eye position이니 $(0,0,0)$이구요.

먼저, Pixel 위치 $(u,v)$를 $[0,1]^2$로 정규화 된 범위에서 받습니다.

그 후 그 Pixel이 (e.g.) $z=-1$ 평면 위에 위치하게 변환하면,

$s = (tan(0.5 \cdot fovx) * (u-0.5), tan(0.5 \cdot fovy)* (v - 0.5), -1)$입니다.

그 후 $s, e$를 inverse view matrix를 곱해서 world frame으로 바꿀 수 있습니다.

Trace()

ray를 쐈으면 그 ray의 최종 색깔도 구해야 겠죠?
그 함수가 trace()입니다.

만약 반사되고 어쩌고 한 ray가 light source에 도달하지 못하고, 영원히 튕기고 튕기고 한다면 그거까지 다 계산할 수는 없으니,

적당하게 쳐내주는 if문이 존재하구요.

intersection이 광원이라면 광원색을 출력하며,
intersection이 없다면 배경색을 출력합니다.

이 3가지가 trace()의 stop condition들입니다.

그러면 ray가 no_intersection인지는 어떻게 판단할까요?
그냥 ray tracing 범위에 거대한 구를 하나 그려서 거기 닿으면 no_intersection이라고 보면 됩니다.

intersect()

Triangle 을 포함, Ray Tracing에서 지원하는 많은 primitive (sphere, cylinder ..)들에
intersect하는지 확인하는겁니다.

Ray-Triangle Intersection Test

먼저, Triangle의 vertice들을 알 때, Triangle 자체를 변수로 표현할 필요가 있습니다.

$p = a + \beta(b-a) + \gamma(c-a), \beta>0, \gamma>0, \beta+\gamma<1$

이렇게 표현할 수 있죠.
이 때 $a, b, c$는 counter-clockwise여야 하구요.

이걸 primary ray인 $e + td$와 연립해서,

$e + td = a + \beta(b-a) + \gamma(c-a)$ 를 풀면,

(여기서 모르는 값은 $t, \beta, \gamma$)

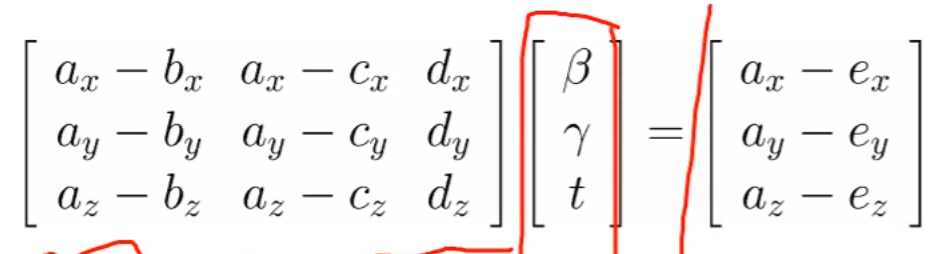
다음 행렬식으로 표현이 가능합니다.

Reflection

3개의 vertex를 아니까 face normal을 구하구요.

그 face normal을 이용해 reflect를 계산합니다.

아까 reflection 식은 구했죠.
$r = d - 2(d \cdot n)n$
이걸 이용해서,

vec3 reflect(vec3 I, vec3 N) {return I - N*dot(I,N)*2.0f}

로 구현할 수 있습니다.

q가 ray고 n이 face의 normal vector일때요.

Refraction

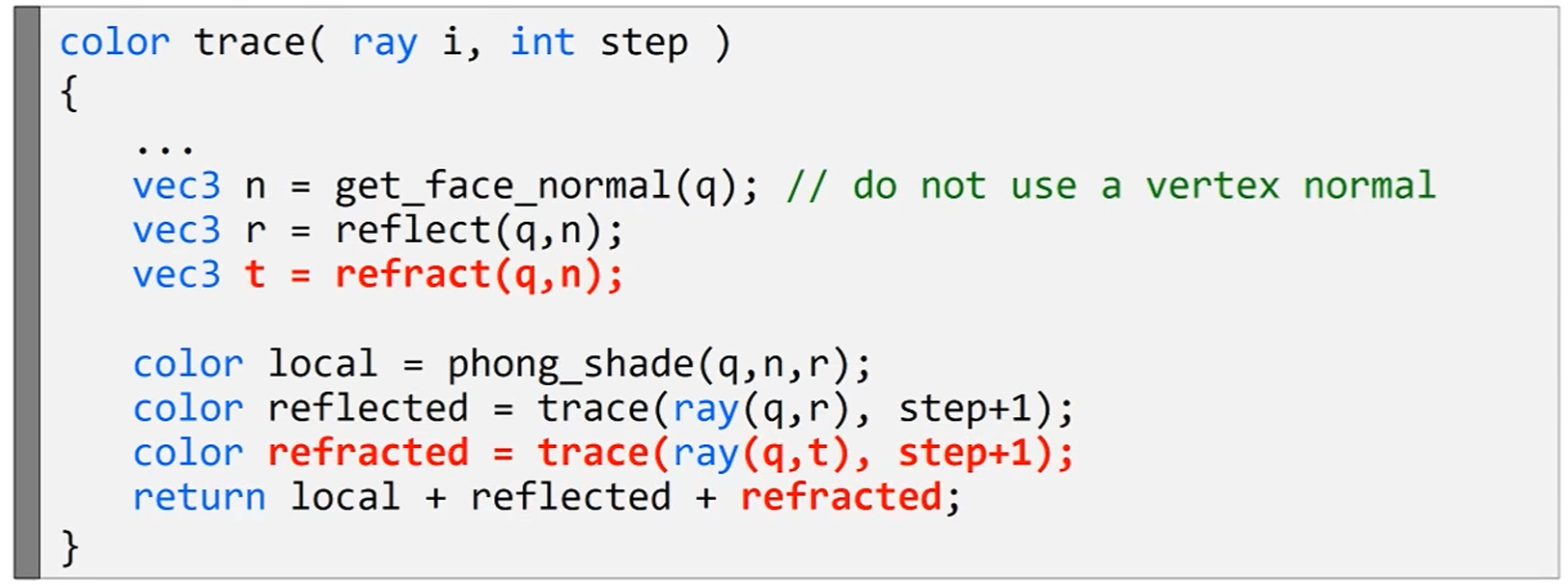
이렇게 쭉 재귀해서 가면 됩니다.

Shadows

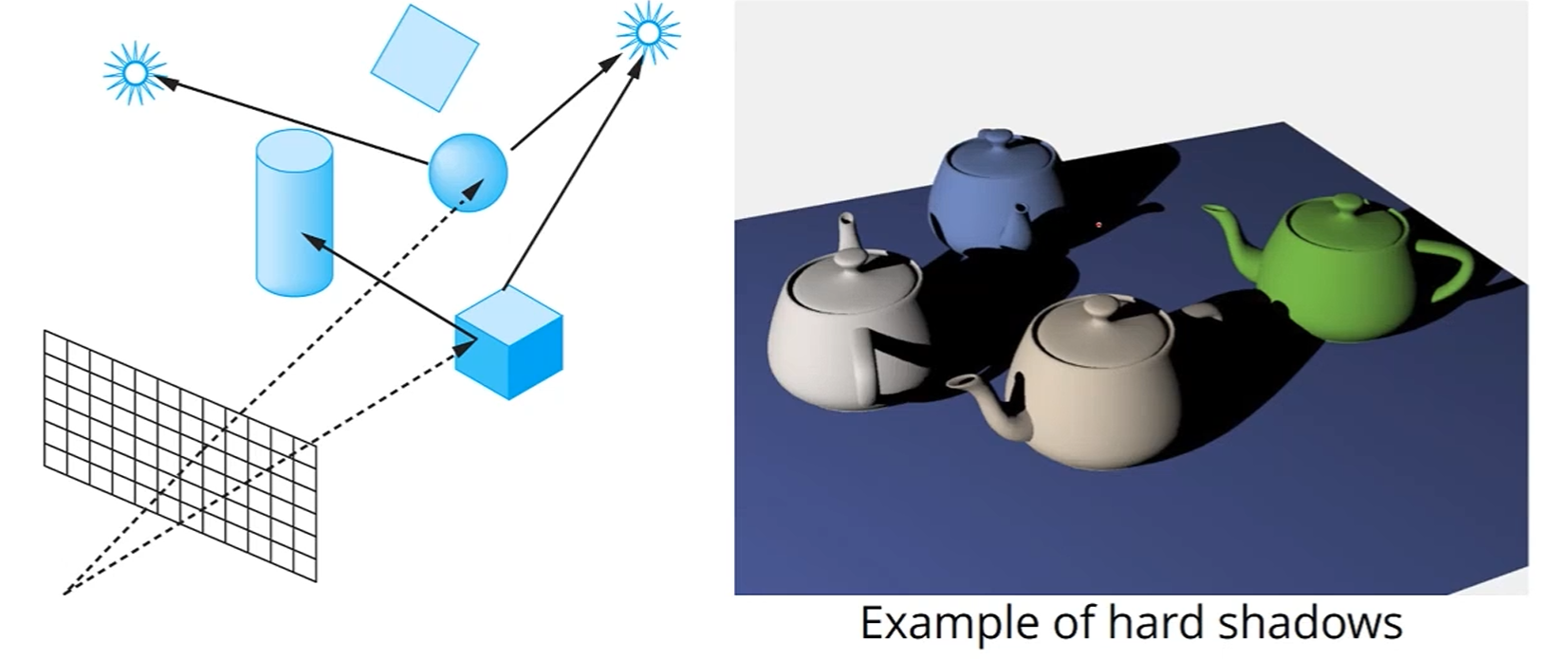
Point가 보이더라도, Point에서 Light Source를 볼 수 없다면
거기는 가려져야 합니다.

그게 Hard Shadow입니다.

Light Source가 많다면, Hard Shadow를 사용하고,
Light Source가 적다면 shadow ray casting을 반복합니다.

엄청 느려질 수 있습니다.

Soft Shadows

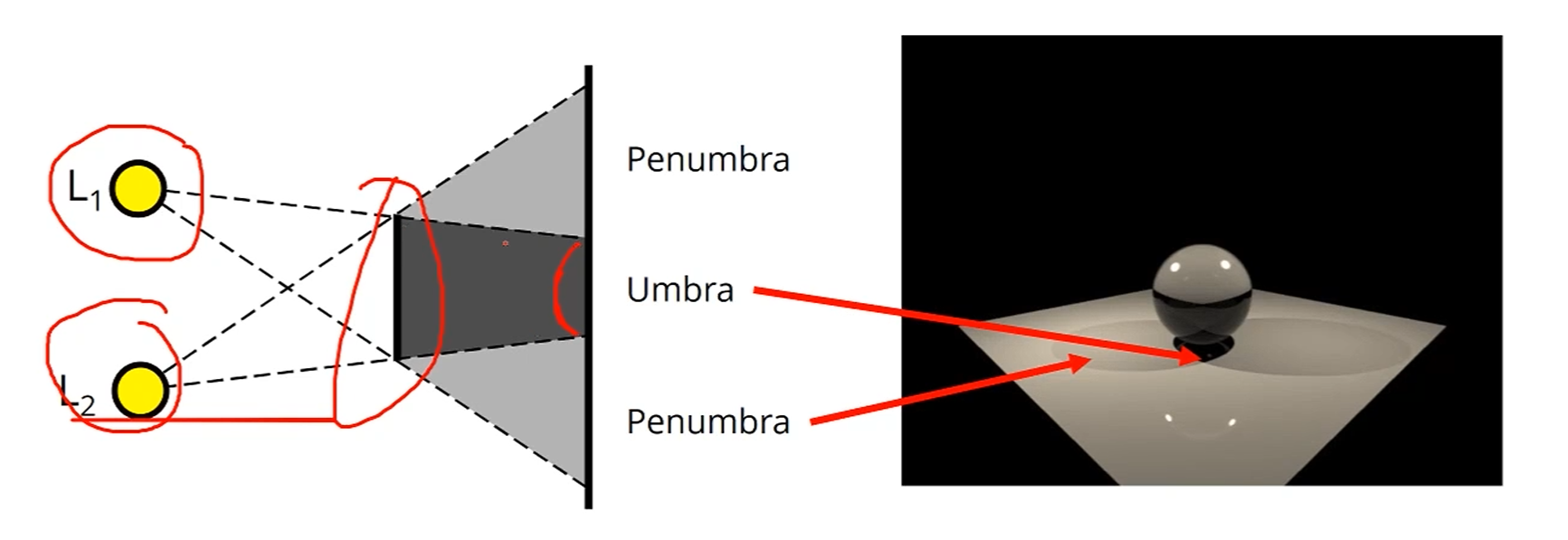
전에 배웠듯, Umbra와 Penumbra가 존재하는 구조입니다.

Dispersion

굴절율은 빛의 파장에 따라 달라집니다.

유리의 굴절율이 1.5라고 하는 것도 노란 빛 (wavelength 587.6nm) 기준이죠.

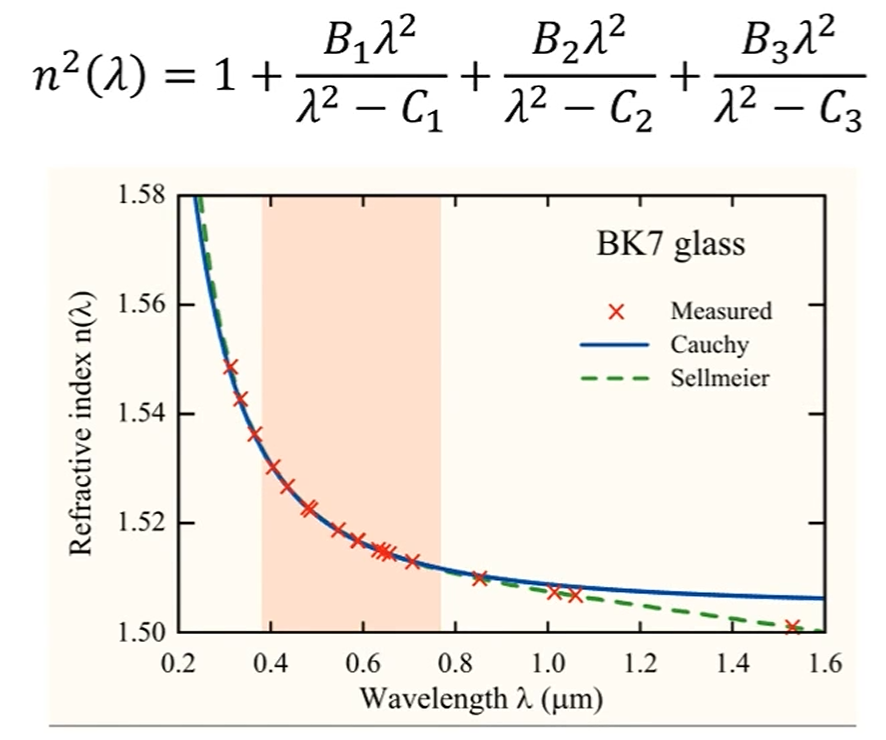
다음 공식을 이용하면 전체 wavelength에 대해 굴절율을 다르게 적용할 수 있습니다.
이 공식은 Sellmeier의 공식이고, Cauchy의 공식도 있습니다.

Fresnel Equation

빛이 반사될 때 얼마만큼이 반사되고 얼마만큼이 굴절될까요?

1:1 비율일까요?
그걸 알려주는 공식입니다.

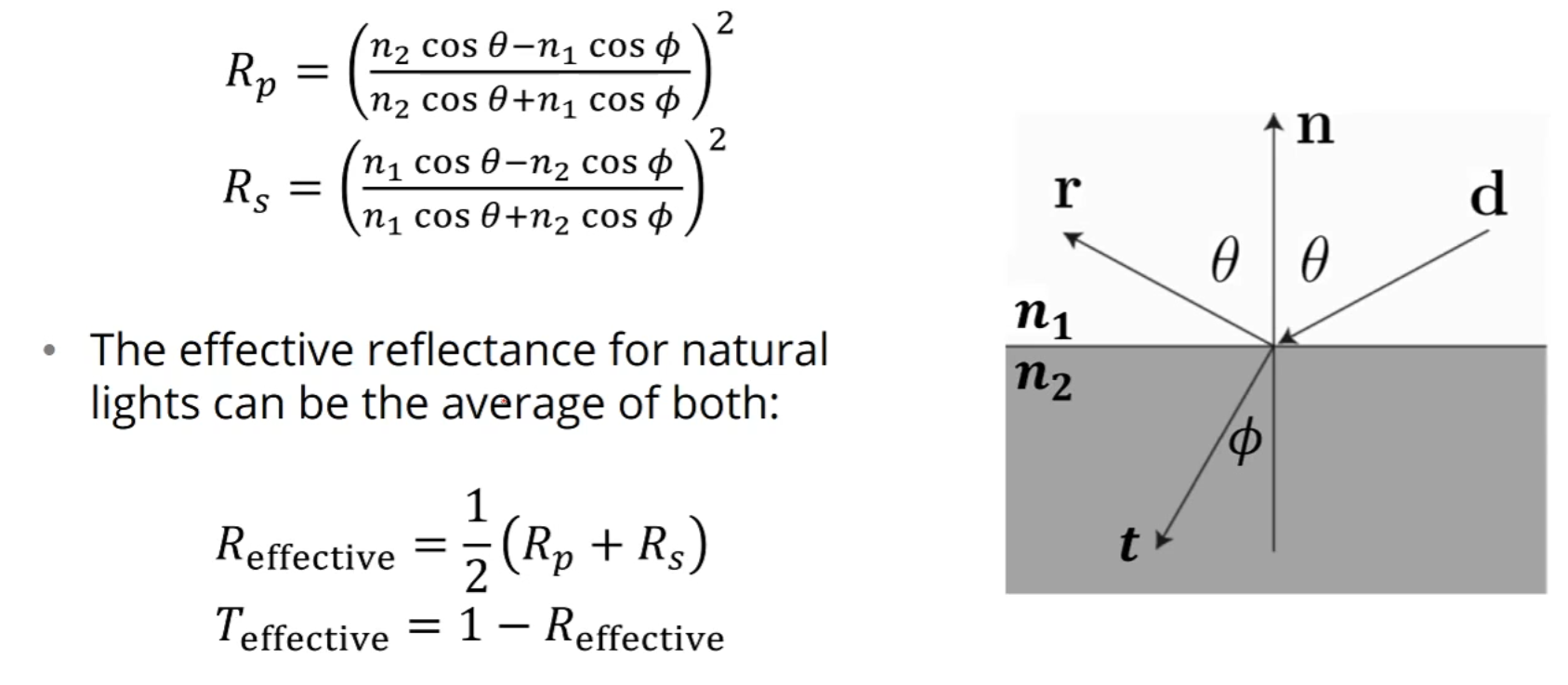
자연광의 경우는 여러 빛이 섞여있기 때문에, 평면편광 $R_p$와 수직편광 $R_s$의
평균치를 사용합니다.

그 평균 반사치에서 뺀 만큼은 당연히 굴절치겠구요.

Fresnel 반사식은 너무 복잡하죠?
위의 Fresnel 반사식에서 norm과 평행하게 들어오는 빛의 경우는,

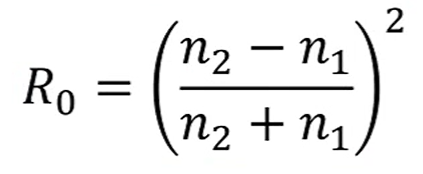
다음과 같이 approximate가 가능합니다.

이 때,각 $\theta$에서의 반사율 역시 approximate가 가능한데,
$R(\theta) = R_0 + (1-R_0)(1-cos\theta)^5$로 쓸 수 있고,

이것을 Schlick approximation이라고 합니다.

차이가 조금 있죠?
유리에서 반사된 값이 투영된 모습입니다.