Shading
Shading은 색깔을 바꾸는 것입니다. 근데, Light와 Material의 interaction을 고려합니다.

단순히 이미지만 칠해놓은 것은 Color나, Albedo라고 부릅니다.
Light-Material Interaction
빛이 있으면, 빛의 입자/wave가 뿜어져 나오죠.
일부는 흡수되고 일부는 반사될 겁니다.
물체의 색깔이나 밝기는, 반사되는 빛의 양에 의거하는 것을 다들 알 겁니다.
Light source and Materials
크게 4가지를 알아야 합니다.
-
광원 (Light Source)
-
Surface Material
표면이 얼마나 미끌하고 거칠하냐, 그래서 반사도가 달라지냐. -
Surface Orientation
Surface에도 다 방향이 있습니다.
그걸 normal vector를 이용하여 가르킵니다. -
Location of Viewer
Viewer (나)의 location이 필요합니다.
Abstract Modeling
정확히 하는건 아니고, 추상적으로 모델링하는 내용입니다.
Light Source와 Surface Material은 abstract하게 모델링 됩니다.
물론 Geometry는 이미 수학적으로 나타나 있어서 정확합니다.
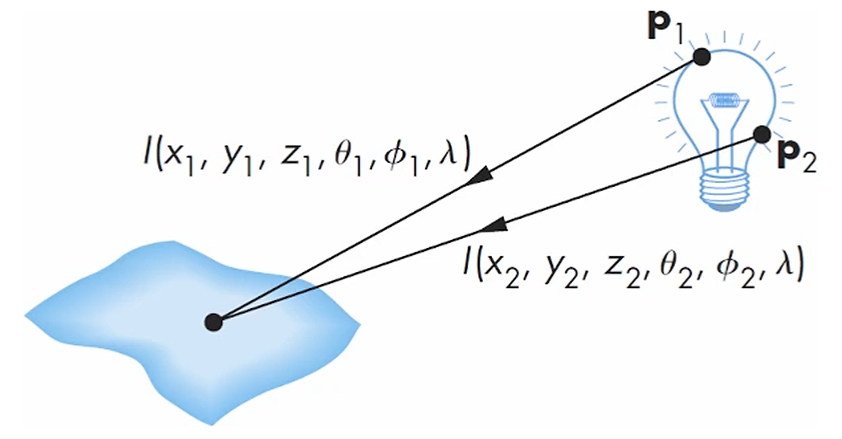
가령 General Light의 경우는, (전구)
전구의 빛을 모델링하기 위해선 막 적분하고 여러고 저쩌고 해야 합니다.
하지만 그걸 simplify하기 위해서, abstract modeling을 사용합니다.
Light Source Model
간단화된 light source model은 3가지가 있습니다.
- Point Light Source
- Distant Light Source
- Ambient Light
Point Light Source
Light Source를 Point와 Color로 모델링 하는 것입니다.
심플하죠.
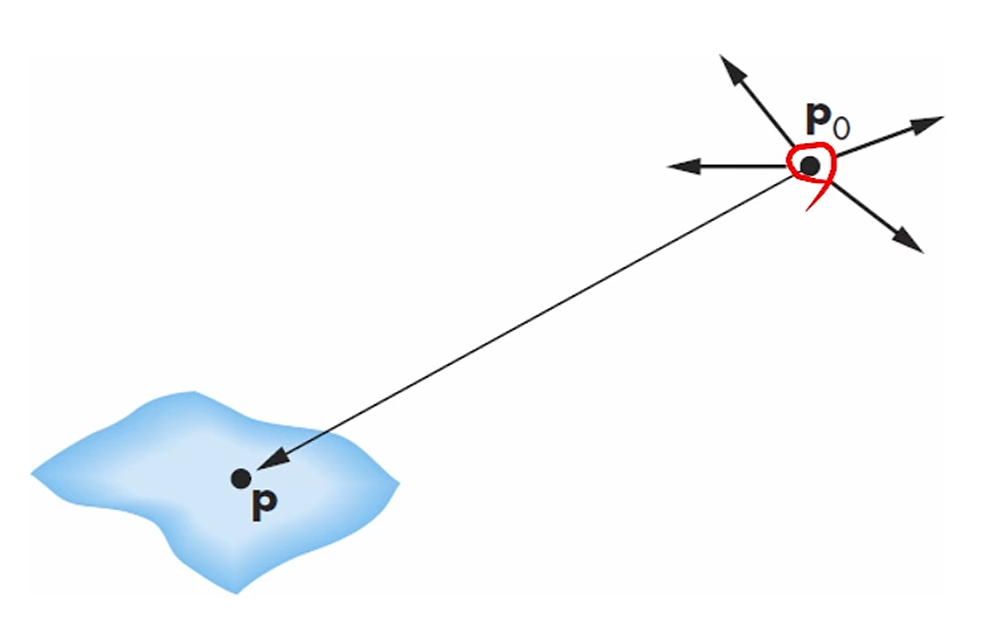
좀 더 물리적인 내용을 넣고 싶으면 Distance Attenuation을 넣어도 됩니다.
Directional(Distant) Light Source
빛이 태양에서부터 일자로 들어온다고 생각합시다.
Vector로만 표현됩니다.
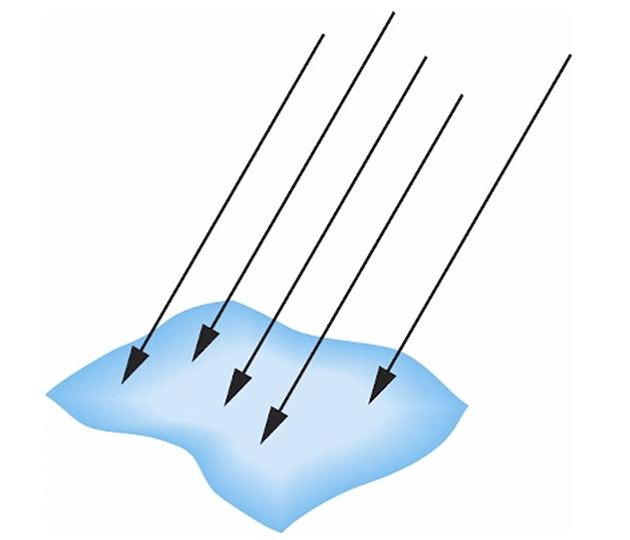
즉, HC에서 마지막 w값이 0이겠죠.
Ambient Light

빛이 우리 주변에 살고 있다고 생각하는 것입니다.
밤에 불 끄고 있을 때도 살짝씩 보이는 것을 Ambient라고 개념적으로 생각하면 됩니다.
구현할 때는, 그냥 constant한 기본 색 offset을 더하는 것으로 구현합니다.
Indirect는 물체끼리 반사된 빛을 말하구요.
Direct Light와 합쳐야 실제같은 예쁜 빛이 나옵니다.
물론 Indirect Light는 계산량이 어마어마합니다.

그래서, 그냥 Average color를 취해내서, Ambient로 정의하고,
Direct에 더해서 approximate 하는 방식입니다.
물론 approximate가 심하기 때문에, 안 하는게 낫습니다.
Surface Materials
Microfacet model
물체의 표면이 전부 매우 작은 거울이다. 라는 모델입니다.
surface material의 기초가 됩니다.
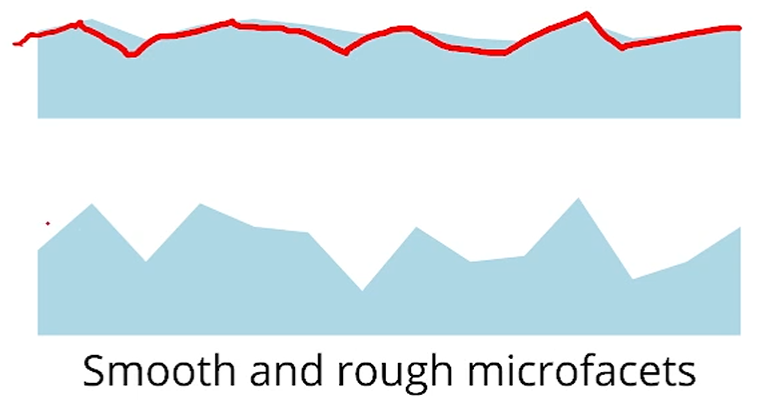
물체 표면의 분포에 따라 반사도가 달라진다를 가정하기 위해 가져온 모델입니다.
Specular / Glossy Model
명백히하면 Specular가 거울반사, Glossy는 거의거울반사입니다.

이런 surface를 Glossy surface라고 얘기하구요.
가운데 빛이 완전히 반사되고 있는 부분이 Specular Highlight입니다.
그 외에는 glossy하기 때문에 빛이 되게 퍼져서 반사되는 것을 볼 수 있죠.
Diffuse Reflector
Diffuse는 난반사입니다.
정반사가 아니라, 랜덤하게 반사하는 거죠.
이상적으로, 모든 direction으로 동일하게 난반사시키는 diffuse reflector가 있는데,
그건 Lambertian surface라고 부릅니다.
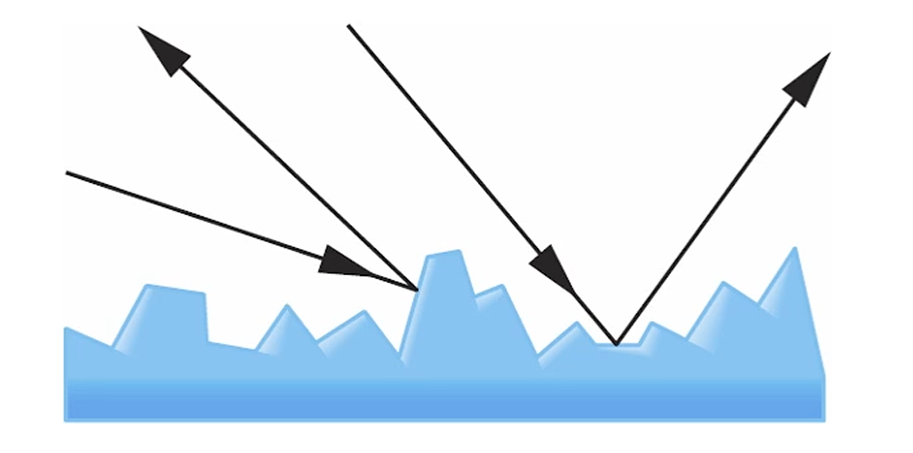
Surface 자체는 microfacet이지만,
엄청 울퉁불퉁 해서 마치 난반사인 것 처럼 보이는 모델인 것입니다.
이상적으로,
surface가 완벽하게 rough하거나 smooth할 수 없습니다.
그래서 보통 둘을 섞습니다.
그래서 surface material을 지정할 때,
Diffuse와 Specular를 따로 지정하고 따로 계산한 다음 더합니다.
물리적으로는 말이 안 되죠.
이 아이디어, 즉 light와 surface를 분해한 다음 합치자라고 한 것이
Phong Illumination Model입니다.
Phong Illumination Model
직관적으로, 관찰을 통해 정해진 model입니다.
물리적으로 정확하진 않고, intuition으로 만들어진 model입니다.

빛과 surface를 3가지 요소로 쪼개서 합치는 것입니다.
Specular는 사람의 시선과 관련이 있는 요소입니다.
반사된 부분이 우리의 눈에 들어와야 하잖아요.
Diffuse는 반대로 View-independent합니다.
광원하고만 연관이 있습니다.
Phong을 위해선 4가지 vector가 필요합니다.
- light source : (광원으로 가는 방향 vector입니다.)
- To viewer :
카메라로 가는 vector죠.
그래서 원래는 인데, Camera Space에서 shading을 한다면 Camera Space의 위치가 원점이니까, 가 성립합니다. - Normal vector :
- Ideal Perfect Reflector :
이상적으로 정반사될 때의 각도입니다.
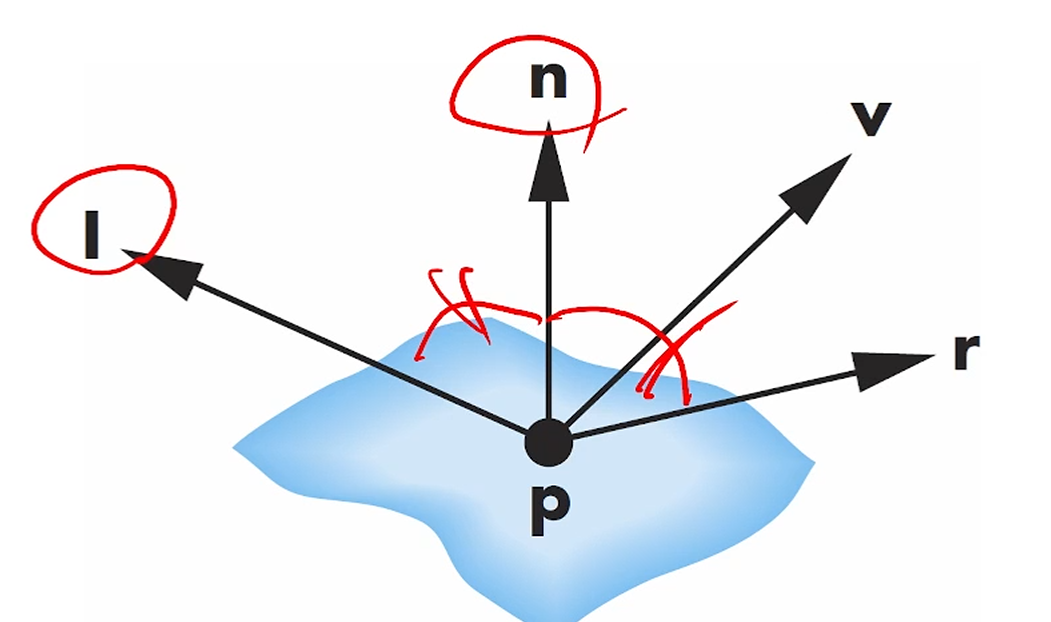
나머지는 다 있는건데, 은 과 을 이용해 정의를 해줘야겠죠?
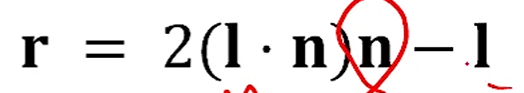
이렇게 정의할 수 있습니다.
이제 준비는 끝났습니다.
Ambient Reflections
Ambient Light는 들어오는 빛의 색과 Material Property에 따라 정해집니다.

Material쪽에서 정의되는 reflectance는 로 씁니다.
반사량이기 때문에, 0~1 사이에서 정의됩니다.
들어오는 빛의 양을 로 쓰면,
들어오는 빛이 얼마나 반사되어 나오는지, 즉 Ambient가 나옵니다.
Diffuse Reflections
Diffuse는 ambient와 비슷하게 로 시작합니다.
이 때, 반사되는 빛의 양은 Geometry에 영향을 받죠.
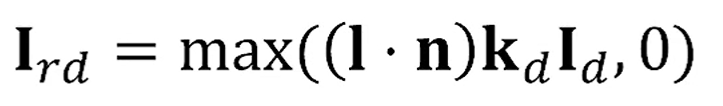
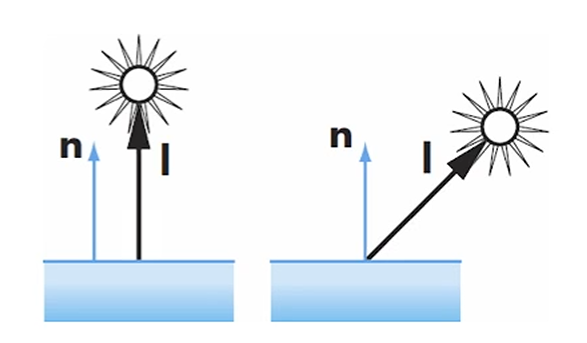
다음과 같이 정의됩니다.
광원과 normal vector가 반대방향일 때는 가 음수가 되니까,
를 이용해 막아줄 필요가 있습니다.
은 Angular Attenuation이라고 부릅니다.
여기에, 거리에 따라 빛이 줄어드는 Distance Attenuation을 적용하면,
로 적을 수 있습니다.
이 때 는 로 적을 수 있는데요, 이건 별로 안 좋은 계산입니다.
암튼 에 반비례하기만 하면 된다.
Specular Reflections
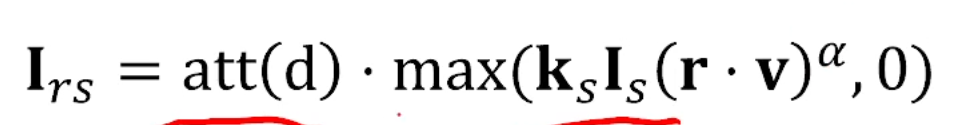
이렇게 적을 수 있습니다.
똑같이 Distance Attenuation이 적용되며,
특이한 내용이 하나 붙죠.
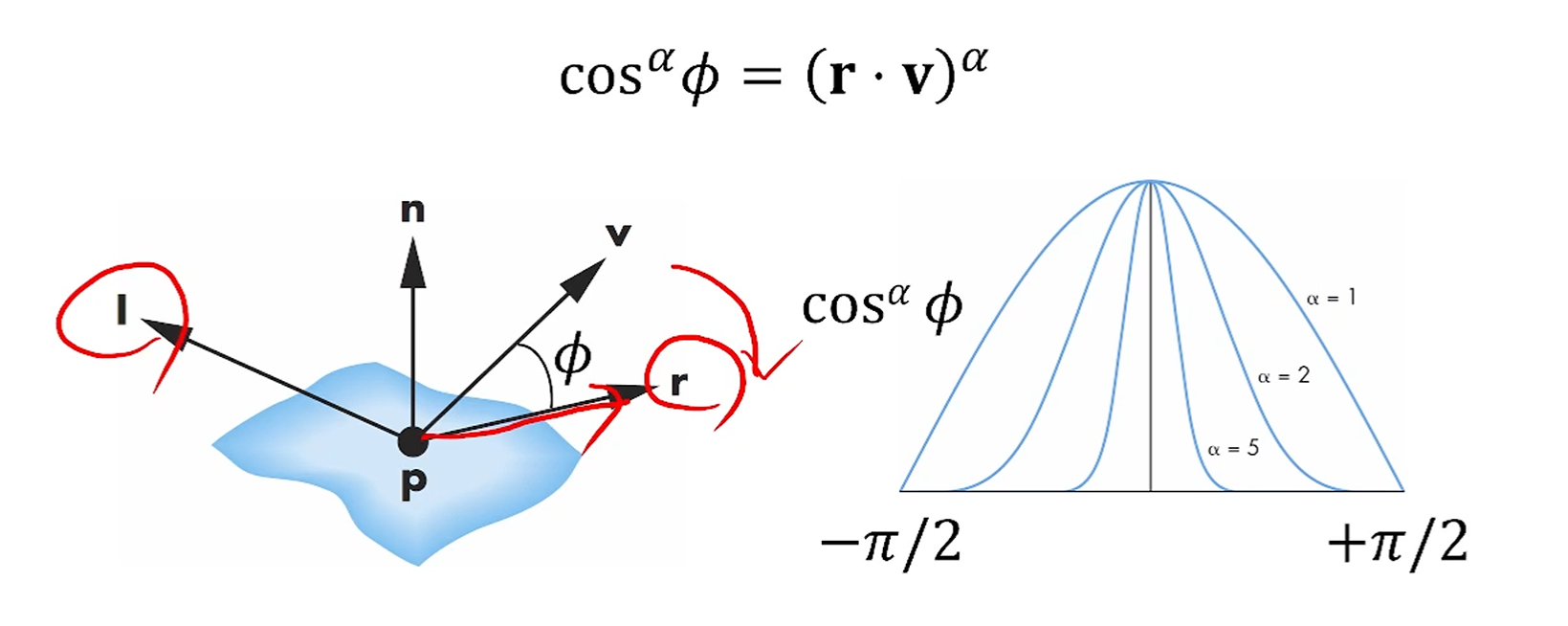
그림에서 봤을 때, 정확한 거울반사라면 v = r일 때 정반사겠죠.
즉, 과 가 가까울수록 세기가 세지고, 멀어질수록 세기가 꺼지겠죠.
즉 과 사이의 각도가 중요한데,
각도의 영향을 보이기 위해 를 쓸 때, 만 쓰면 좀 많이 퍼지니까,
각도가 작을 때만 확 퍼지고 조금이라도 멀어지면 덜 퍼지게 하기 위해서,
를 지수로 하여 를 계산합니다.
는 알아서 찾으면 되구요. 보통 10~20 정도가 plastic, n백~1천 근처면 metal.
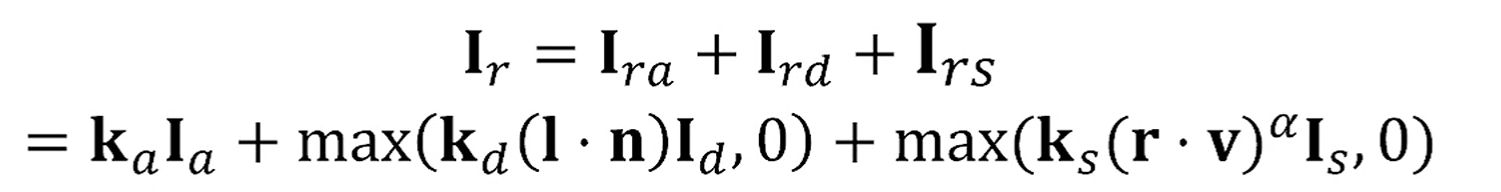
그걸 다 합치면 Phong Model이 완성됩니다!
Blinn-Phong Model
Blinn-Phong Model은 Phong Model의 Specular 쪽에 approximation을 더 주는 것 입니다.
Specular 계산식이
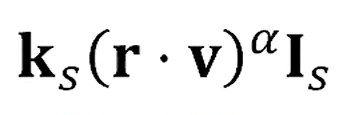
였죠?
근데, 여기서 을 계산하려면, 이었는데,
아 이거 어떻게 예쁘게 못 바꿀까라는 것이 의도입니다.
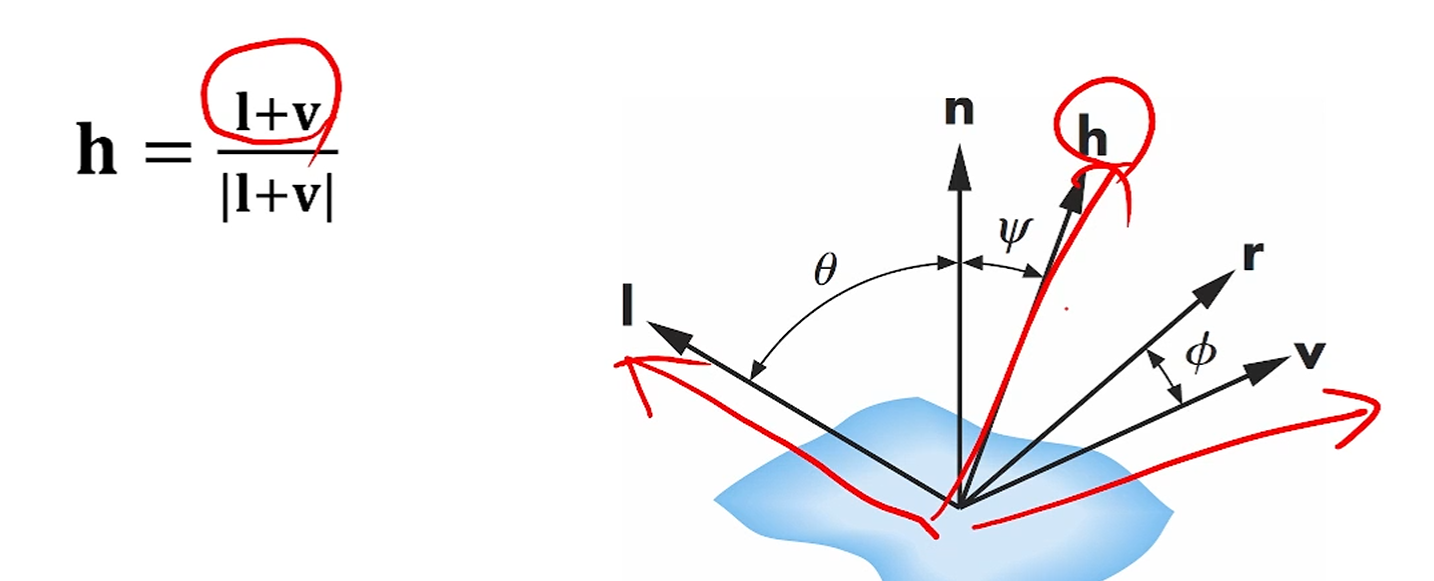
이 때, 원래 r과 v 사이의 각도를 보던 것을,
l과 v 사이의 halfway-vector인 h를 소개해서,
n과 h 사이의 각도로 보자 라는 것이 Blinn-Phong approach의 핵심입니다.
만약, 가 과 같은 plane 내에 있다면, 임도 보일 수 있구요.
아무튼 쉬워지죠.
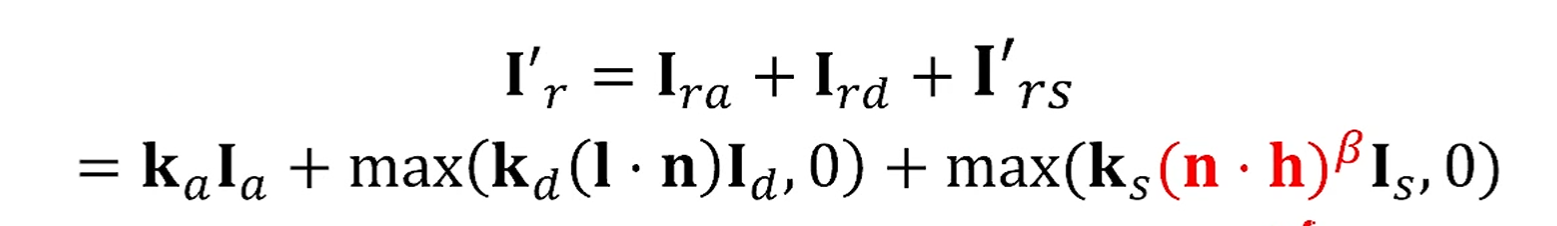
지금 보면 대신 를 썼죠.
도 알아서 찾으면 됩니다.
Polygonal Shading (Effects of Normal Vectors)
지금까지 한 것들은 Point에 대한 Shading이었구요.
Practical하게 구현하려면 모든 point에 대해 shading을 할 수가 없죠.
결국 pixel이나 fragment에 대해 shading을 적용하게 될텐데,
거기서 중요한 건 normal vector입니다.
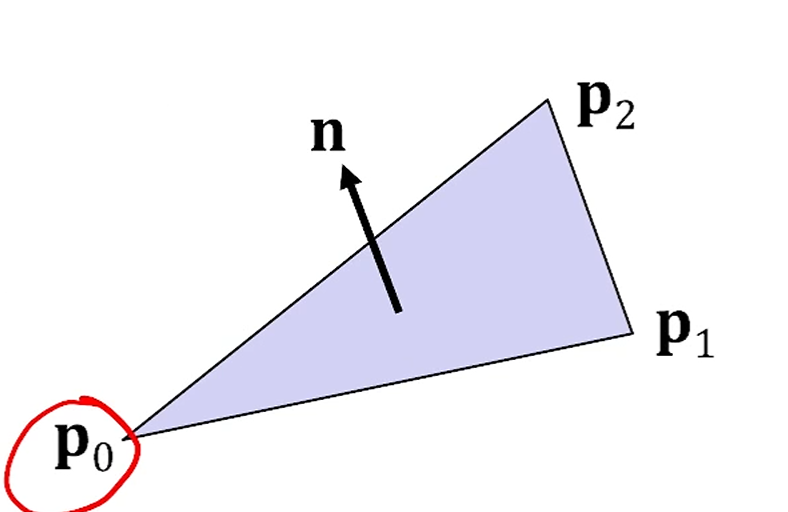
수학적으로 normal vector는 Face당 1개씩 생깁니다.
Per-face죠.
계산식도 외적을 이용하여 이구요.
근데, 그런 식으로 normal vector를 이용해 shading을 하면,

이렇게 뚝뚝 끊겨서 보입니다.
왜냐면 face별로 normal vector가 다 다르잖아요.
바로 옆에 붙어있는 애랑도 다른걸요.
뭐 물론 삼각형을 엄청 많이 만들면 되지만, 이렇게 삼각형이 적은 경우에도
적용을 하고 싶다는 겁니다.
그래서 Interpolation이 가능하게끔 만듭니다.
Vertex Normal
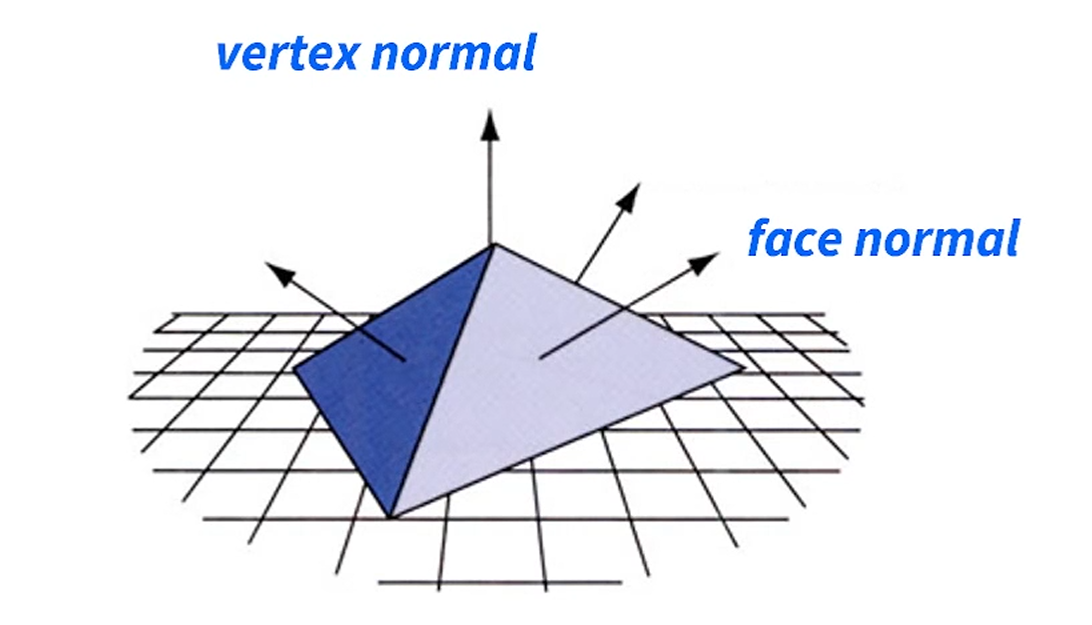
Vertex는 Point인데, Point에 대해 수직일 수 있나요? 안되죠.
Vertex가 있으면 인접한 Face들이 있고 Face Normal들이 있죠.
그 Face Normal들의 평균을 내는게 Vertex Normal입니다.
물리적으로는 말이 안되지만 얼핏 말이 될 것 같기도 하고..
그래서 나중에 Raster에서 Interpolate하면서, Normal끼리 부드럽게 이어지게 됩니다.
그래서 그래픽스에서 Normal을 얘기하면, 언급이 없다면 보통 Vertex Normal입니다.
Vertex Normal을 써서 Shading을 하는 3가지 방법이 있습니다.
- Flat Shading (이건 Face Normal을 쓰는겁니다.)
- Gouraud Shading
- Phong Shading

Raster에서 interpolation할 때 뭘 기준으로 interpolation하냐에 따라서 두가지로 나누는 겁니다.
Raster에서 'color'를 interpolate하면 Gouraud Shading,
Raster에서 'normal'을 interpolate하면 Phong Shading.
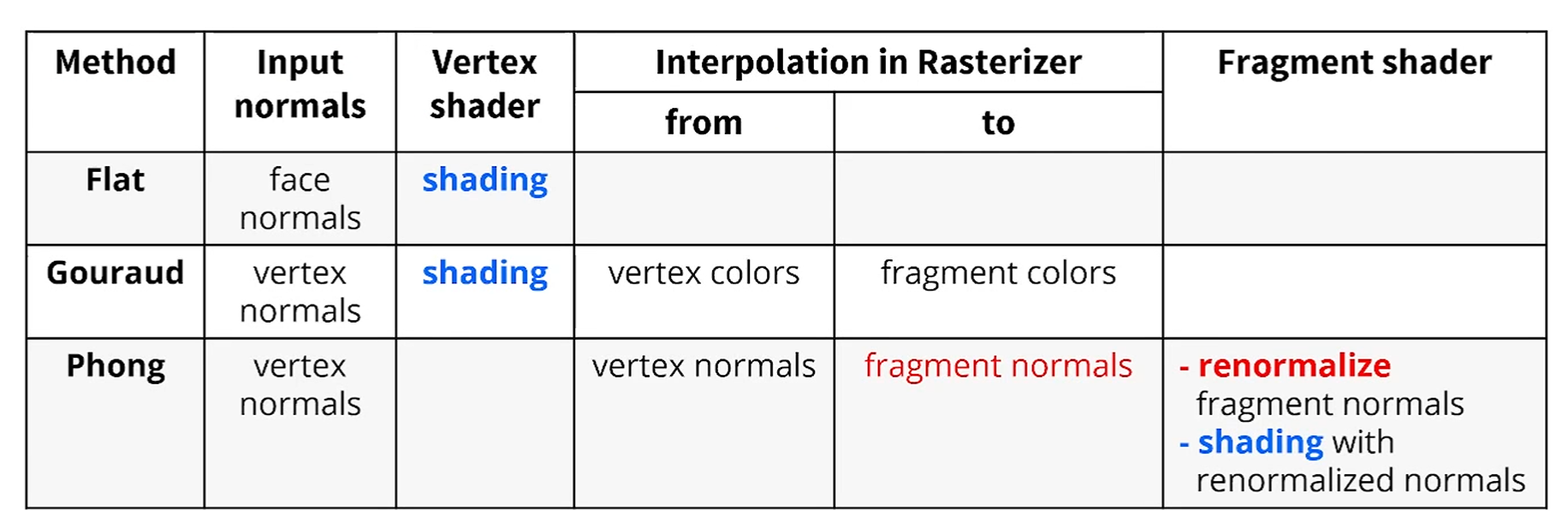
우리가 만들 수 있는 Shader가 2개입니다. Vertex Shader, Fragment Shader.
Flat Shader와 Gouraud Shading은 shading을 Vertex Shader에서 계산합니다.
그 다음 Raster에 색깔을 넘기면, fragment shader는 아무것도 안했죠.
Phong Shading은, vertex normal을 넘기면,
Rasterizer가 interpolate하여 fragment normal을 만들고,
Fragment Shader에서 그 normal로 그림을 그립니다.
옛날에 Vertex Shader에서 Flat이나 Gouraud shading을 쓰며, 거기서 Shading을 했기 때문에
Vertex Processor가 이름이 Vertex Shader가 된겁니다. 역사적 이유가 있죠.
Normals in Phong Shading
Per-fragment normal들은 rasterizer가 linear하게 interpolate 시켜놓습니다.
근데 그러면 일부 벡터들이 짧아집니다.
그래서 다 같은 length를 가지게 normalize할 필요가 있습니다.
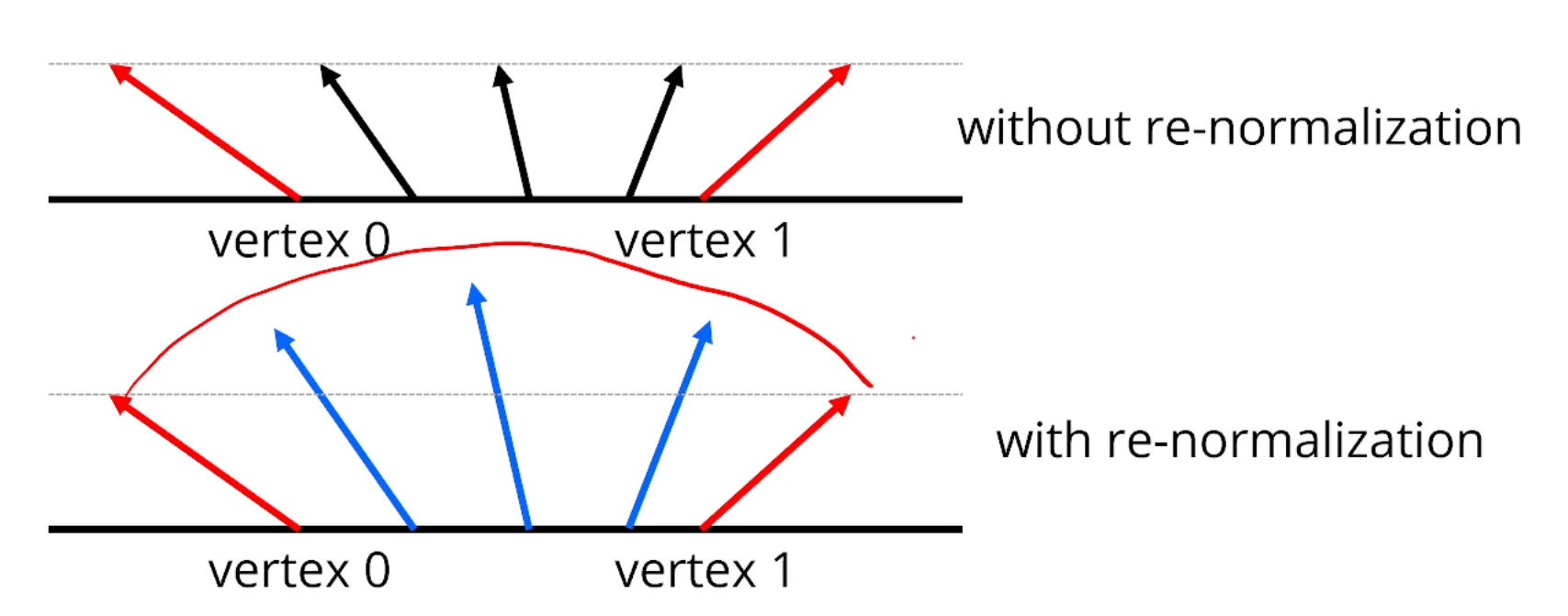
그래야 구형 곡면을 따라서 부드럽게 휘죠.
Gouraud vs Phong Shading

기본적으로 Phong Shading이 더 부드럽습니다.
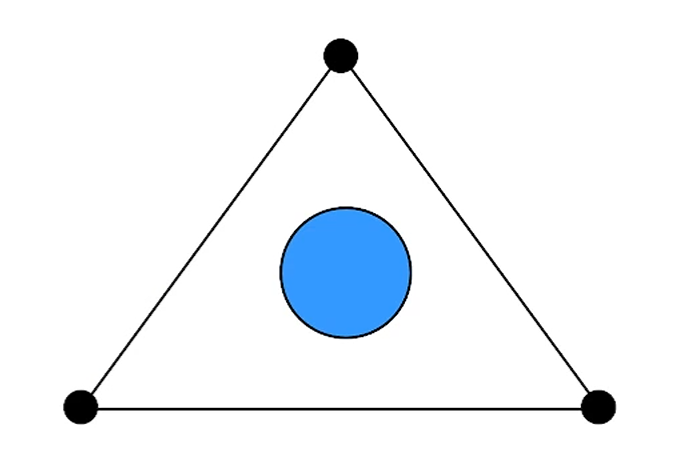
가령 이런 삼각형 내에서,Gouraud Shading을 쓴다면 highlight가 삼각형 중앙에 있을 때 color가 interpolate되지 않고 highlight를 놓칩니다.
하지만 Phong Shading은 normal을 interpolate하기 때문에, 다 잘 챙길 수 있습니다.
polygon들이 작아진다면 둘이 비슷하겠지만,
polygon이 커지면 이런 문제들이 드러나기 때문에,
기본적으로 Phong Shading을 쓰는 게 좋습니다.
Phong shading vs Phong illumination model
둘은 다릅니다! Phong씨가 만들었다고 다 같은게 아니에요.
전자는 vertex normal을 interpolate하여 per-fragment normal을 사용하는 shading 기법이구요.
후자는 shading을 ambient + diffuse + specular로 나눠서 하는겁니다.
