3. Geometry

Vector Space

Vector Space는 Vector의 Set.
Vector Space의 element를 Vector라고 부릅니다.

일반적으로 고등학교 때 배우기로 방향과 벡터가 있다- 라고 배웠는데,
Vector Space는 Field F에 대해서 정의된 set V입니다.

여러 요소를 만족해야 하는데, 간단히 정리하면

• Vector는 더해질 수 있고, 더해진 값도 벡터입니다.
• 벡터합에 0벡터와 역원이 존재합니다.
• Vector는 Scalar로 곱해질 수 있습니다.
• scalar multiplication에 있어 항등원이 존재합니다. (1)

Geometric Elements

Geometry란, n-dimensional space에서 object간의 관계를 보는 학문입니다.

Computer Graphics에선, 보통 3차원까지만 관심이 있고,
Point, Line, Triangle, Quad같은 기하학적 object를 갖고 작업을 합니다.

이것들을 정의하고, 이것들의 관계를 얘기할 수 있지요.

크게 3가지. Point, Scalar, Vector가 근본적으로 중요한 element들입니다.

Point

space에 있는 한 location을 나타냅니다. 위치.

point(점)은 size도 없고, shape도 없습니다.

기하학적 object를 정의하는 데에 좋습니다.
물론, point만 가지고 정의할 수는 없지요.

가령 point 사이의 거리? 이런 것들을 나타내는 요소를 scalar라고 합니다.

Scalar

스칼라, 스케일러, 아무튼 Scalar.

얘는 덧셈, 곱셈을 잘 정의할 수 있는 Object의 Set이라고 부릅니다.
결합, 분배, 역원, 항등원이 다 정의 되어 있습니다.

실수, 복소수의 예시가 있습니다.

당연히 Scalar만으로는 아무런 효과가 없습니다.

Vector

물리적 설명은, 방향과 크기가 있는 quantity라고 얘기합니다.
이렇게만 얘기하면, Space 내에서 location이 존재하지 않게 되죠.

Point는 Location만 있었고,
Scalar는 Distance만 있었고,
Vector는 방향만 있습니다.

이걸 다 합쳐야 무언가 만들어지겠죠?

Operations on vectors and points

space 내에서 vector가 의미를 가지려면 위치, 즉 point가 필요합니다.

만일 point에서 point를 뺀다면,
vector가 나옵니다. (방향)

비슷하게, point에다 vector를 더하면
point가 나옵니다. (위치)

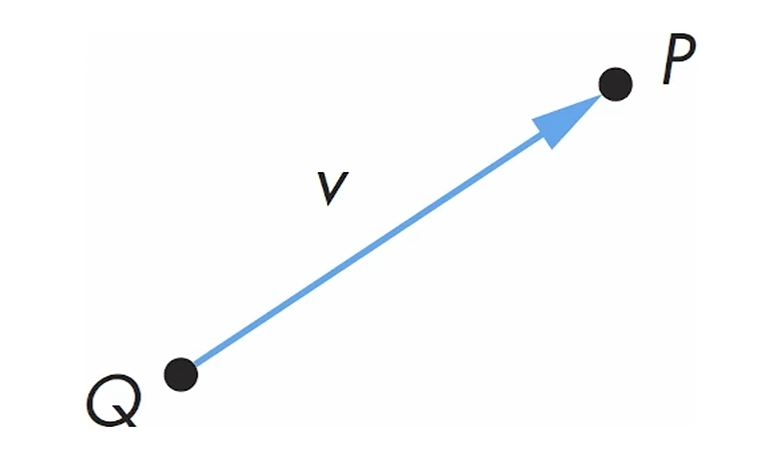
v = P-Q고,
P = Q+v죠.

CS View on Geometric Elements

우리가 컴퓨터에서 저것들을 표현하려면 어떻게 정의해야 할까요?

가령 GLSL같은 경우,
vec2, vec3, vec4라는 컨테이너에 point, vector, color를 정의해 넣을 수 있습니다.

일단 저 storage 안에 값들을 정의해서 넣고,
필요한 operation은 프로그래머인 우리가 직접 코딩해서 넣는거죠.

Euclidean Space

유클리드가 만든 개념입니다.
Vector Space + Distance

space 내에서 최단거리를 나타내는 distance가 더해집니다.

Affine Space

Vector space에 Point를 포함시킨 개념입니다.

앞서 Vector Space에선 Vector와 Scalar만 포함되어 있었기 때문에,
V+V, VxS, SxS같은건 다 정의가 되어 있었습니다.

여기에 Point를 추가함으로서,
Vector + Point operation을 정의합니다.

Vector + Point를 함으로서 새 Point를 정의할 수 있게 됩니다.

Affine Space에 Point가 생겼다 한들, Point와 Scalar의 관계는 아무것도 정의하지 않았음을
알고 있어야 합니다.

Representation

Vector Space, Euclidean Space, Affine Space같은걸 정의 했을 때,

그것과 관련 없이 정삼각형이라는걸 정의할 수 있겠죠?

세 변의 길이가 같으면 정삼각형이잖아요.

근데, 우린 Euclidean Space와 엮어서,
그 안에서 좌표 3개를 잡고,
좌표끼리 이어서 그 변의 distance들이 다 같으면 정삼각형이라고 얘기합니다.

이런걸 Representation이라고 합니다.

Additional Elements on Geometry

Lines

Affine Space에서 Line은 Point + Vector의 sum으로 표현됩니다.

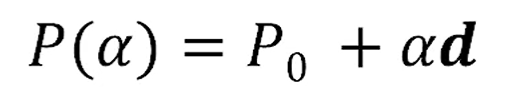
이 Parametric Form에서,
점 $P_0$과 $d$ 벡터랑 더해서 점 $P(a)$를 정의할 수 있는데,

이 때 $a$를 아주 많이 잡으면? 그 점들의 집합이 Line이 되는 겁니다.

그리고, $a$를 $a\geq0$으로 정의하면, Q에서 P로 쏘는 반직선, ray가 되구요

$a$를 $[0,1]$로 정의하면 $Q$와 $R$ 사이의 line segment가 됩니다.

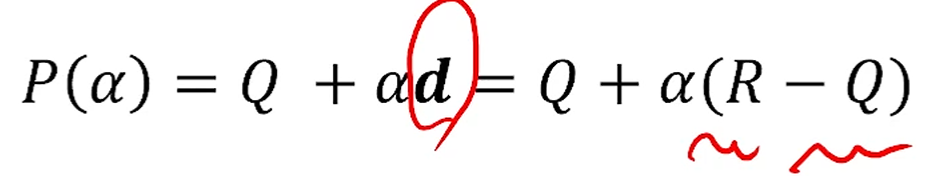
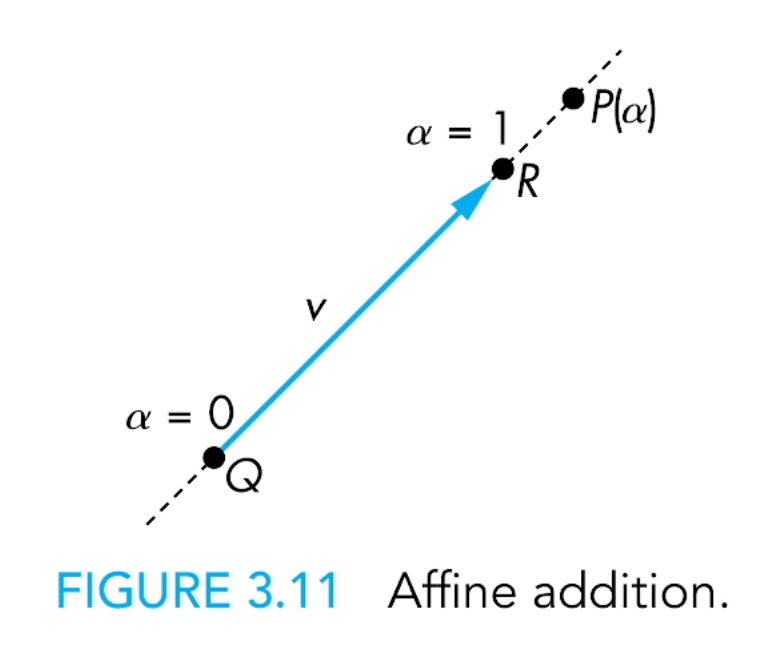
Affine Sum

Point + Point나,
Point * Scalar같은건 정의가 되어 있지 않았죠? affine space에서요.

하지만 아주 제한적인 형태의 더하기가 가능합니다.

그걸 Affine Addition이라고 부릅니다.

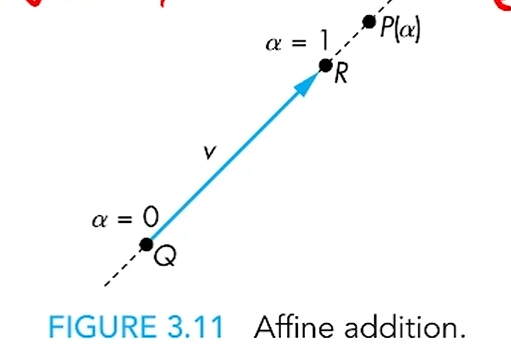
scalar인 $a$와 point인 $R, Q$는 서로 연관이 없어야 하지만,
일시적으로 가능하다. 라고 정의를 하면,
다음과 같이 정리가 되는데,

이런 특수한 형태가 나오는 경우에만 SxP, P+P가 정의가 가능해집니다.

조금 더 일반적으로 써 보면, $P = a_1Q+a_2R$인데, $a_1+a_2=1$이 되어야 합니다.

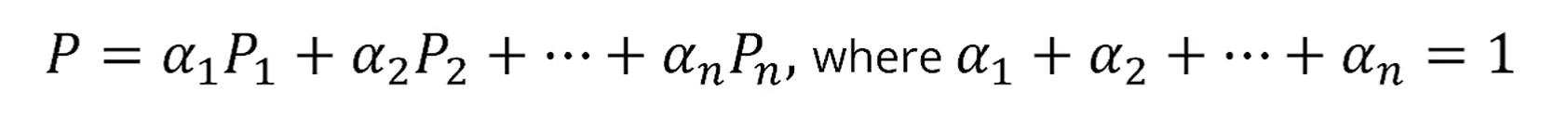
이렇게 계수합이 1이 되면 Point의 addition을 정의할 수 있고,
이걸 affine addition이라고 부릅니다.

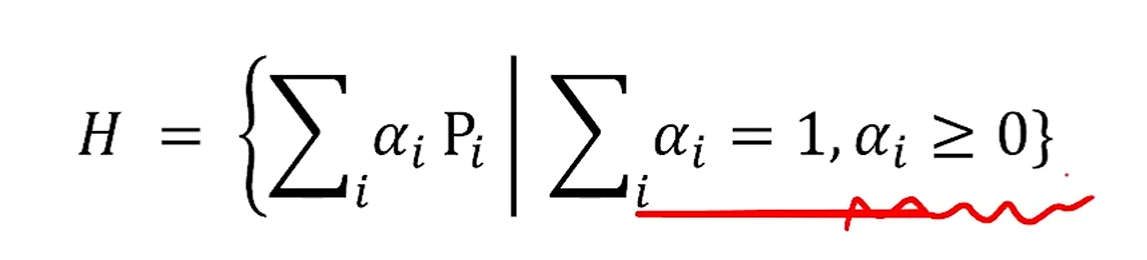
좀 더 확장하면, point들의 계수합이 1이면, 이렇게 Point끼리 더할 수도,
Scalar와 Point의 곱을 정의할 수도 있게 됩니다.

Convex Hull

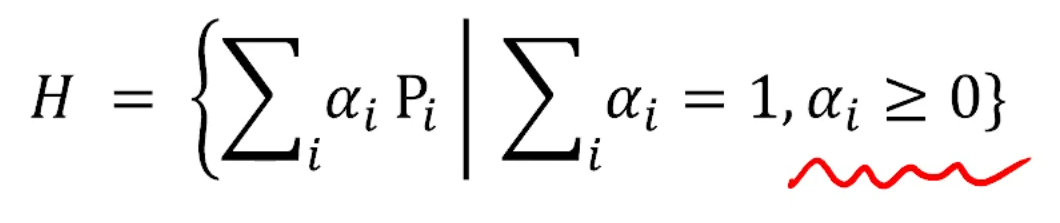
계수 합이 1이다에서, 각 계수들이 0 이상이다라는 조건을 하나 더 붙입니다.

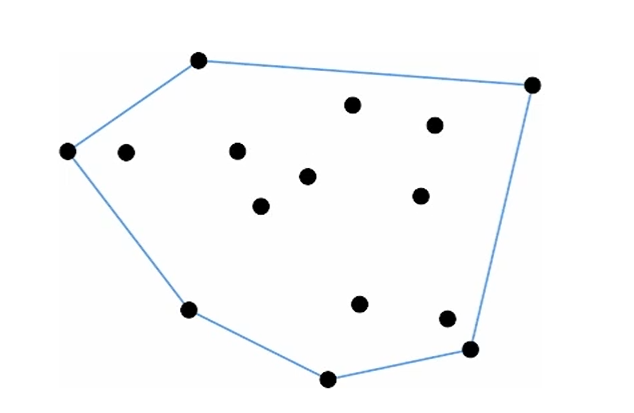
convex hull에서 다각형을 정의할 수 있습니다.
이 모든 point를 다 포함하는 가장 작은 convex object를 convex hull이라고 하구요.

convex object는 object 내의 어떤 두 점을 골라도,
그 두 점간의 line segment가 object 안에 무조건 존재하면 convex object라고 합니다.

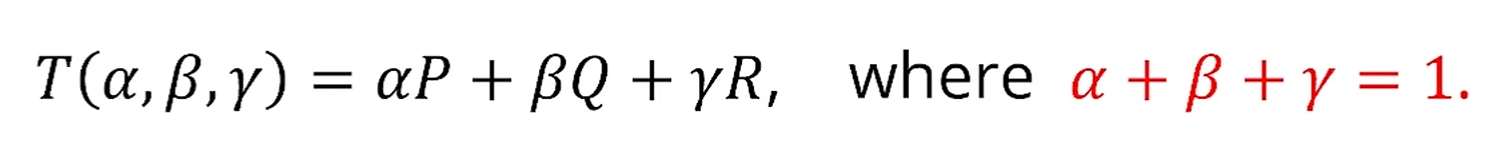
affine sum의 관점에서 Triangle 역시 다음과 같이 정의할 수 있습니다.

이 때, $\alpha, \beta, \gamma \geq0$ 조건을 포함한다면,
이 영역은 Triangle과 그 안의 영역을 포함하는 representation이 됩니다.

따라서 Triangle은 minimum한 convex hull이 됩니다.

이런 식으로 Triangle과 그 내부를 정의하는 좌표계를
barycentric coordinate라고 부릅니다.

무게중심 좌표계.

Geometric Modeling

Model

Model은 실제 세상을 수학적으로 Abstract하는게 Model입니다.

CG에서, 우린 Geometric object를 이용해 modeling을 합니다.

주로 쓰는 building block은 아주 작고 minimi한 primitive를 사용합니다.
Point, Line, Triangle 등.

일반적으로, Triangular Mesh가 매우 흔합니다.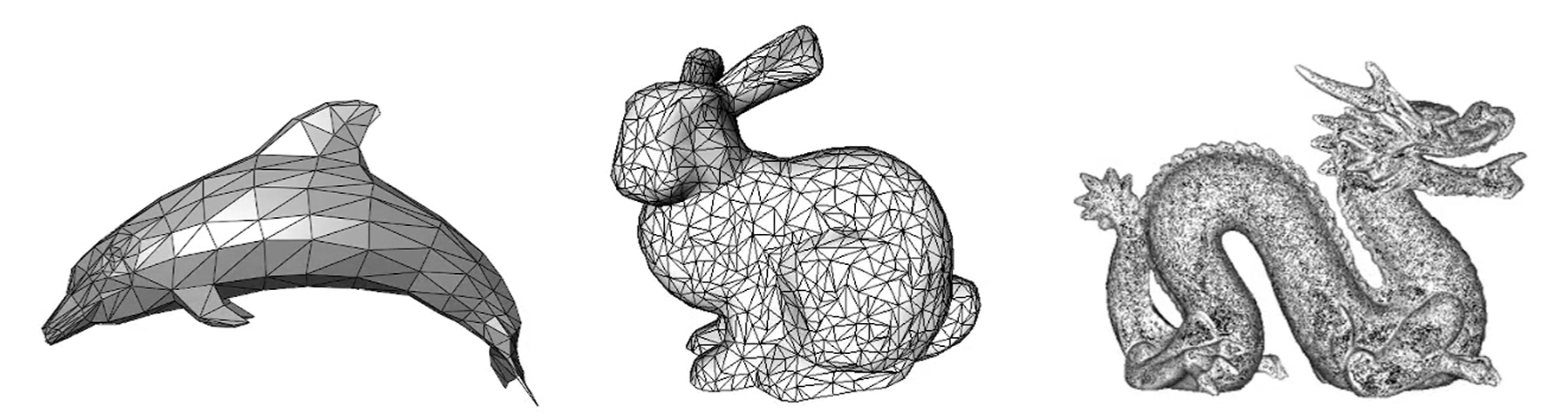

세상을 삼각형으로 표현하는거죠. 아주 잘게 쪼개서요.

3D Primitives

graphics HW와 SW에 가장 맞는 object가 뭐냐?
2D Surface입니다.

그게 뭔가요?

껍데기만 있고, 내부는 비어 있는 mesh를 의미합니다.

내부가 차 있는 object는 volumetric object라고 부르고,
CT나 MRI처럼 내부가 중요할 때 쓰죠.

우린 이 3d object들을 vertex의 set으로 정의합니다.
vertex끼리 잘 연결해서 잘 만듭니다.
가장 optimize된 성능을 얻기 위해선 sphere든 circle이든 전부 삼각형을 잘 엮어 만듭니다.

왜 이렇게 하냐?
많은 graphic system은 Triangle 기준 최적화가 되어 있습니다.

초당 1억개 이상의 삼각형을 그릴 수 있습니다.
Vertex 단위로 처리하면 앞서 나온 Pipeline architecture에 맞게 병렬적으로 처리하기도 좋구요.

그럼 왜 하필 삼각형일까요?
그건 삼각형은 무조건 한 평면 위에 있기 때문입니다.
flat해요.

polygon들은 한 plane에 없을 수가 있습니다.
하지만 삼각형은 그렇지 않죠. 합리적 이유죠?

Triangular Mesh Representation

이 Triangular Mesh들은 어떻게 표현될까요?

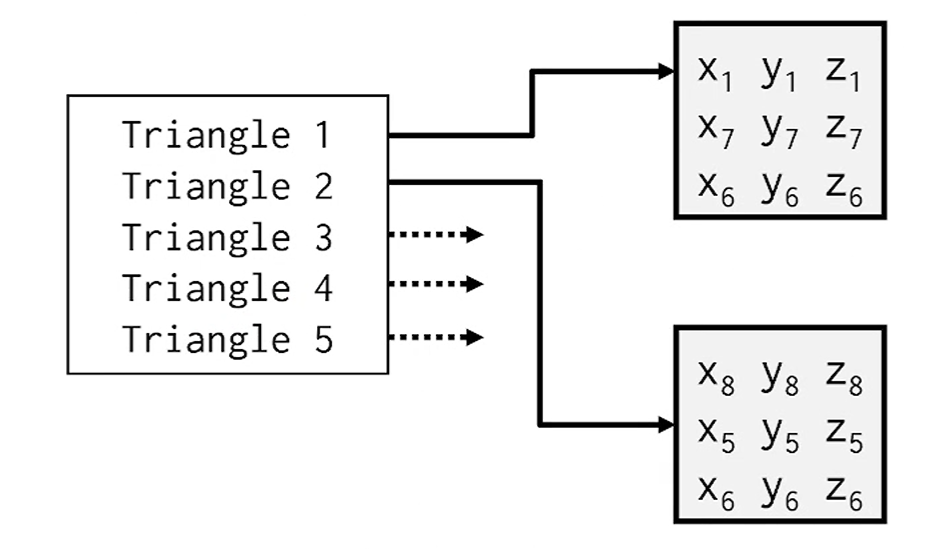
다음과 같이 정의가 된 Triangle들은 그냥 Vertex단위로 정의가 될 수도 있죠?

근데, Vertex들은 중복이 있을 수도 있고, 겹치면 불편하고 비효율적이게 됩니다.

그래서 Geometry와 Topology를 분리하게 됩니다.

위상기하학적으로 컵과 도넛은 Topology가 같습니다.
Geometry는 다르죠

Geometry는 vertex의 위치들이니까요.
Topology는 vertex와 edge들의 구조적인 모습입니다.
붙어있는 연결관계를 생각하면 됩니다.

즉, Vertex를 바꿀 수는 있지만 Vertex를 바꿈에 있어서의 연결관계는 그대로 가져가고 싶다.
라는 생각에

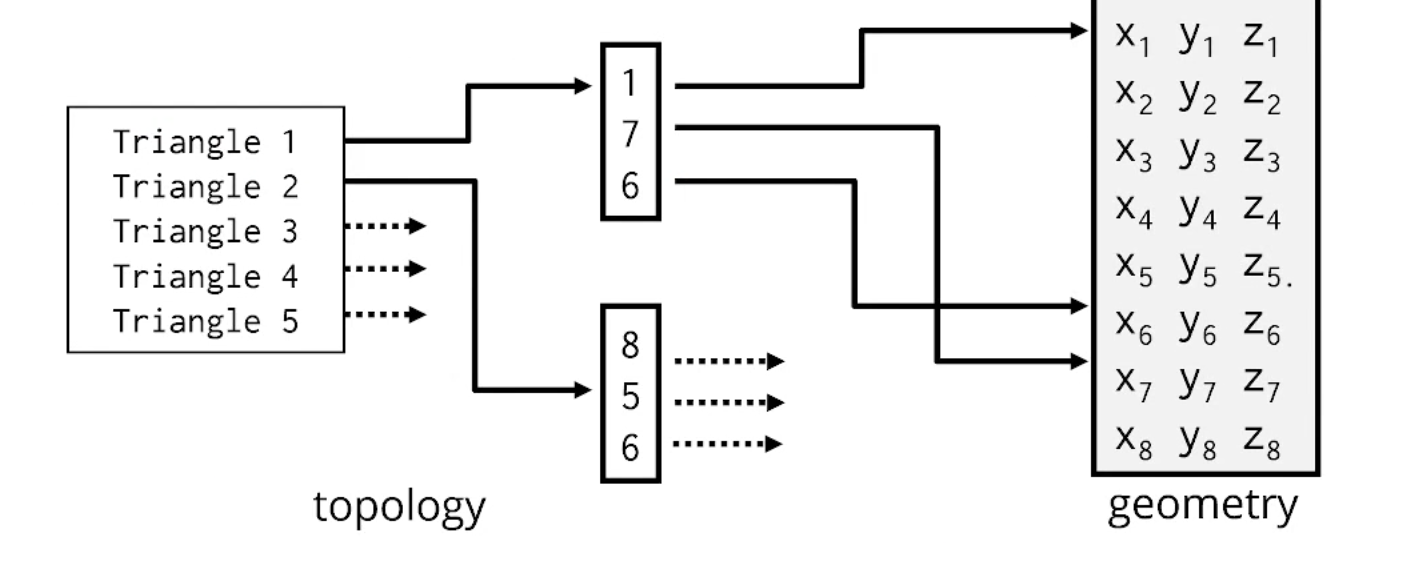
Vertex의 Index를 나눠 Topology로 저장합니다.

즉, V[1], V[4], V[7]이 하나의 삼각형을 그립니다- 처럼 저장하는거죠.
걔네가 어느 위치에 있는지는 뭐 크게 중요친 않구요.

이렇게 Index Buffering을 하면, Topology를 분리해낼 수 있고,
Vertex Buffering보다 보통 빠릅니다.

중복되는 Buffer에 대한 Shading의 양을 줄여주기 때문이죠.