4. Transformations

Prerequisites

여러 vector $v_1, v_2, ... , v_n$은
$\alpha_1v_1 + \alpha_2v_2 + ... + \alpha_nv_n = 0$,
iff $\alpha_1 = \alpha_2 = ... = 0$
일 때 linearly independent 하다고 부릅니다.

즉, 하나의 vector를 다른 vector의 합으로 표현할 수 없다 일 때 linearly independent인 거죠.

그리고 vector space에서, n차원이라는 것은,
linearly independent한 vector들이 n개 있다는 뜻입니다.

또, n차원에서, 어떻게 n개의 linearly independent한 vector를 잡든, 걔네는 basis라고 불립니다.

그리고 basis가 존재한다면, 어떤 vector든
$v = \alpha_1v_1 + \alpha_2v_2 + .... + \alpha_nv_n$으로 적을 수 있습니다.

이 때 v의 계수 $\alpha$들을 representation이라고 이야기 하며,
특정한 basis {$v_i$}에 대해 다음과 같이 좌표를 정의할 수 있게 되지요.

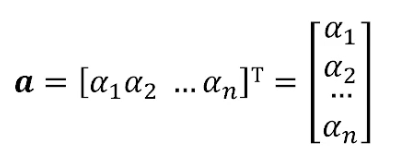
여기까지가 선형대수 기본 내용이었습니다.

알고 시작해봅시다.

Coordinate-free geometry

우린 geometry를 정의할 때 좌표를 정의할 필요가 없습니다.

즉, Point나 Vector를 정의하기 위해 Coordinate System을 정의할 필요가 없다는 거죠.

가령, Euclidean Geometry에서 두 변의 길이와 사이의 각이 같은 삼각형은 합동이다. 라고 정의하잖아요?
여기서 어떤 좌표가 쓰였나요? 아무 좌표도 쓰이지 않았어요.

Geometry의 특성에 대한 것만 알면 되지, 좌표와 굳이 연결지을 필요 없습니다.

근데, 우리는 지금까지 좌표축 잡고 도형을 그리는 geometry를 배워왔는데요?

알죠.
하지만 Geometry가 정의되는 데에 좌표는 필요 없다 라는 사실을 알면 좋습니다.

근데 그러면 쓸 때 문제가 생기잖아요?
어떤 점을 가르킬 때, 저기 있는 파란 점 처럼 얘기를 해야 하니까 불편합니다.

그래서, 이걸 좀 편리하게 부를 수 있는 방법이 없을까? 를 이제부터 얘기해볼겁니다.

Coordinate Systems and Frames

이제, 좌표계를 잡기 위한 기준을 이야기 해보겠습니다.

Point와 Object의 관계를 만들기 위해서, 기준을 잡고, 그 기준에 대해 상대적인 것들을 정의하고자 합니다.

그것이 reference system입니다.

어떻게 기준을 잡냐? 잡기 나름인데, Graphics에선 표준적으로
World coordinates, Camera Coordinates, Screen-space coordinates 등을 씁니다.

예시를 볼까요?

Coordinate Systems

우리가 말하는 '좌표계'는 흔히 Frame입니다.
여기서 얘기하는 '좌표계'는 Vector를 가리키는 것입니다.

특정 vector v를 $v = 2v_1 + 3v_2 - 4v_3$이라고 적을 수 있을 때,
vector $v$의 representation은 $a = [2\ \ 3 \ -4]^T$겠죠?

이러면 $v$에 대한 문제가 생깁니다.

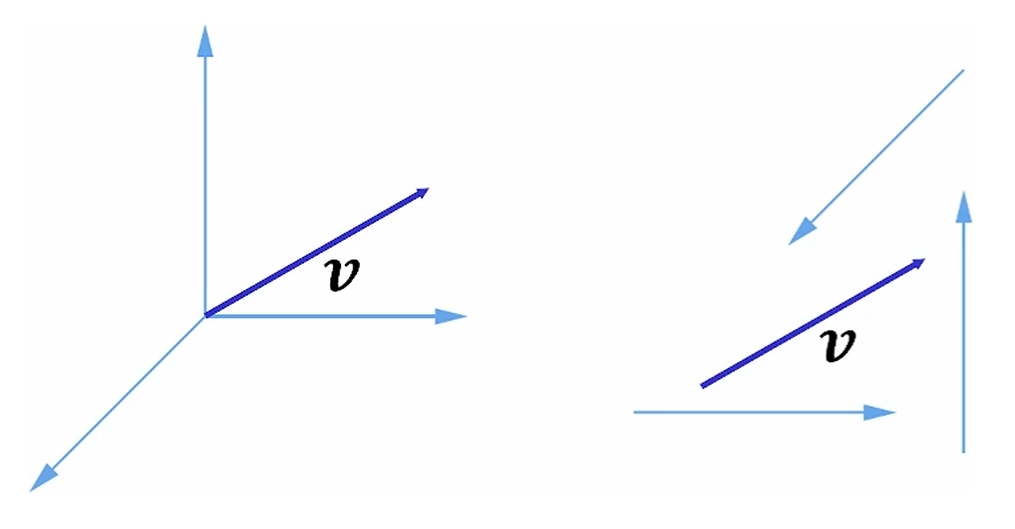
어떻게 되먹은 v입니까?
벡터는 고정된 위치가 없기 때문에, 각 $v_1, v_2, v_3$을 어떻게 잡든 저 v는 말이 됩니다.

지난 시간에 위치는 Point이며, Point + Vector로 Point로 정의하면
그게 affine space라고 배웠습니다.

그래서, affine space에서 기준을 잡으면, 그 기준의 이름을 Frame이라고 부릅니다.
그 때의 single point을 origin이라고 부르구요.

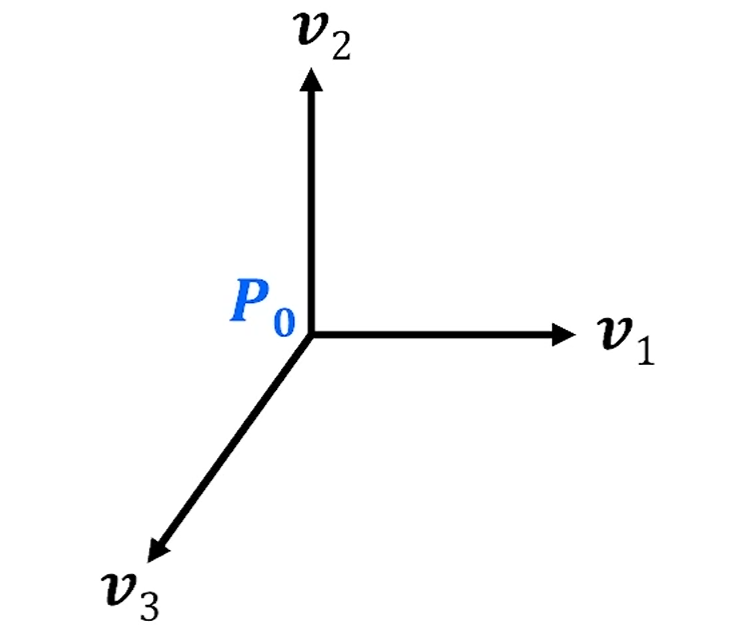
affine space에서 Point를 포함해서 기준을 잡고 싶다- 인 것이고,
그 기준이 Frame인 것입니다.

우리 머릿속에 있던 좌표계죠? 네 그 친구가 맞습니다!

Frames : Representation

Frame은 원점과 basis vector 3개로 이뤄집니다.
즉, $(P_0, v_1, v_2, v_3)$으로 적을 수 있죠.

이 Frame 상에선 모든 점과 모든 Vector가
$v = \alpha_1v_1 + \alpha_2v_2 + \alpha_3v_3$,
$P = P_0 + \beta_1v_1 + \beta_2v_2 + \beta_3v_3$으로 표현이 가능해집니다.

왜? 기준이 생겼잖아요.

물론, Vector는 위치가 없고, 밑의 표현식 (Point)는 위치가 생긴다 라는 점이 다릅니다.

어려운 말 여러번 하고 있는데, 사실 어려운 말도 아니에요.

여기서 추가로 정의를 2개 해봅시다.

$0 \bullet P = 0$, $1 \bullet P = P$라는 정의를 추가하면,
다음 식이 성립합니다.

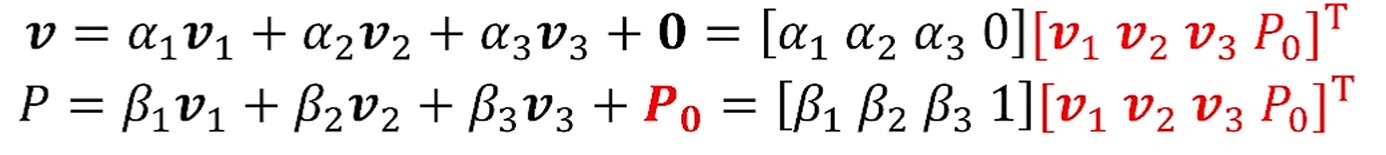
좀 더 모양을 통일해서 썼죠?

Representation의 전항 중 4번째 원소가 0이면 vector, 1이면 Point가 되겠네요.

그래서 찾아보면 vec4로 vector와 point를 나타낼 때, vector는 0, point는 1을 써서 나타냅니다.

Homogeneous Coordinate Representation

방금 한 게 Homogeneous Coordinate Representation입니다.

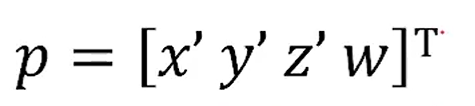
이렇게 나타내는 것이고,
w = 0이면 vector,
w = 1이면 point in 3D,
w가 아무것도 아니면 각 항을 w로 나누면 point가 되겠네요.

CG에선 Homongeneous Coordinate (HC)를 사용합니다.
그래서 모든 transformation, 즉 rotation, translation, scaling같은 건

matrix에 4 x 4 matrix를 곱해서 사용합니다.

General vs Affine Transformations

General Transformation은 mapping 혹은 function입니다.

어떤 vector $u$에 대해 $v = R(u)$, 어떤 point $P$에 대해 $Q = T(P)$로 바꾸는 것이
General Transformation.

General한 Transformation은 그 때 그때 다르기 때문에, 일반적으로 정의할 수가 없고
실제로 쓰기가 힘듭니다.

그래서 우린 정형화된 Transformation이 필요하고,

그게 Affine Transformation입니다.

Affine Transformation

Affine은 Point가 포함된 Affine Space에 관한 것이고,
그걸 잘 정의를 하려면? Frame이 필요합니다!

그럼 당연히 HC가 필요하게 되구요. 자연스러워요.

Frame을 잡는 방법은 무한합니다.

하지만, 한 번 Frame을 잡았다면, 그 때의 Representation은 Unique합니다.

그래서, 그 사이에 변환을 할 수 있어야 하고, 그걸 Affine Transformation이라고 부릅니다.

Affine Space 내에서 Mapping을 끝내고 Line은 Line이고, Point는 Point고, 이렇게 성질이 변하지 않는 것이 Affine Transformation의 특징입니다.

1줄요약 : Representation을 다른 Frame용으로 변환시켜 주는 것이 Transformation.

Affine Transformation의 가장 큰 특징은, 4번째 row가 고정이라는 것입니다.

맨 아랫줄이 0 0 0 1이라면 Affine Transformation입니다.

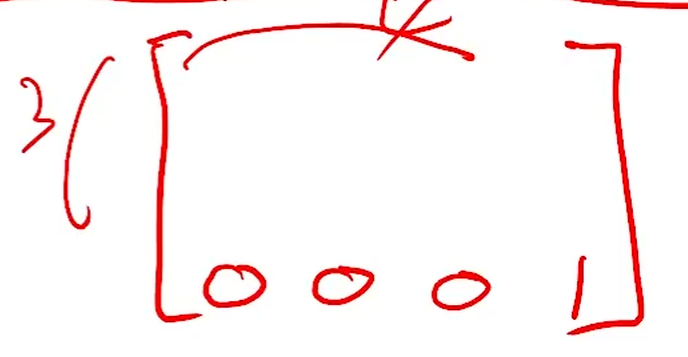
그럼 남은 12개가 우리가 건들 수 있는 Degree of Freedom입니다.

그리고 이 12개는 Translation 3개, Rotation 3개, Scaling 3개, Shear transformation 3개로 나눌 수 있습니다.
이 내용은 좀 이따 볼게요.

Affine Transformation의 특징이 뭐다?
Line은 Line으로, Point는 Point로 남는다.

그 중 Rigid body transformation은 translation과 rotation이 있는데,
이건 object의 모양이 변하지 않는다는 특징이 있으며,

Scaling과 Shear는 object의 모양을 변화합니다.

이 4가지를 포함하는 것을 affine transformation이라고 합니다.

Computer Graphics에서 중요한 점은?

Transformation을 할 때, line의 끝 점만 잘 변환하면 됩니다.
그러면 그 사이를 그냥 이어버리기(interpolation)만 하면 돼요.

왜냐면 affine transformation에서 line은 line으로 유지가 되니까요.

그래서 pipeline approach에 매우 잘 적합한 것이죠.
앞서 pipeline에서 line 대신 vertice를 보냈던 이유가 이겁니다.

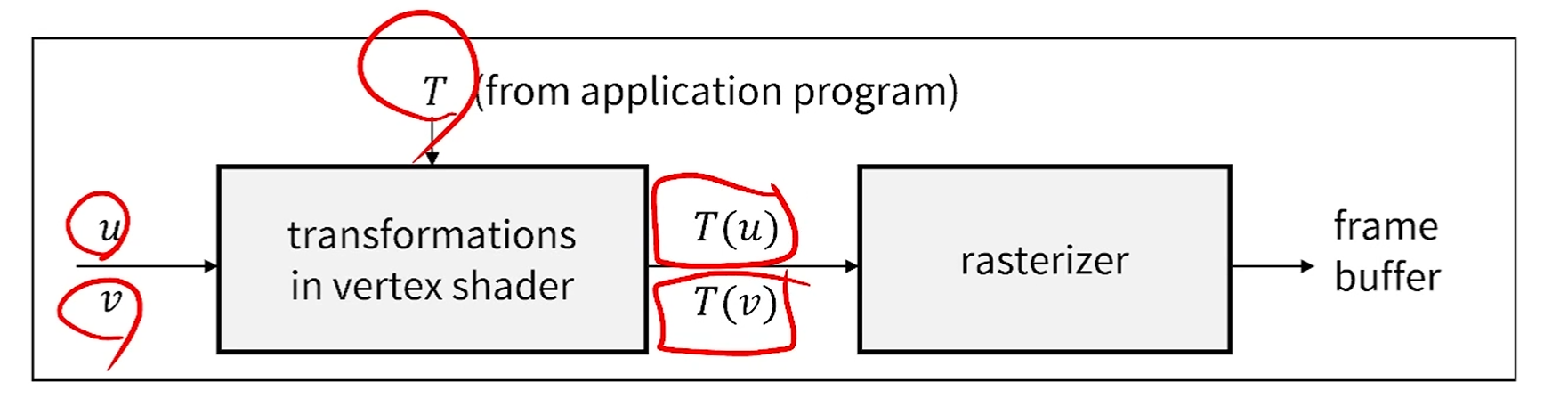
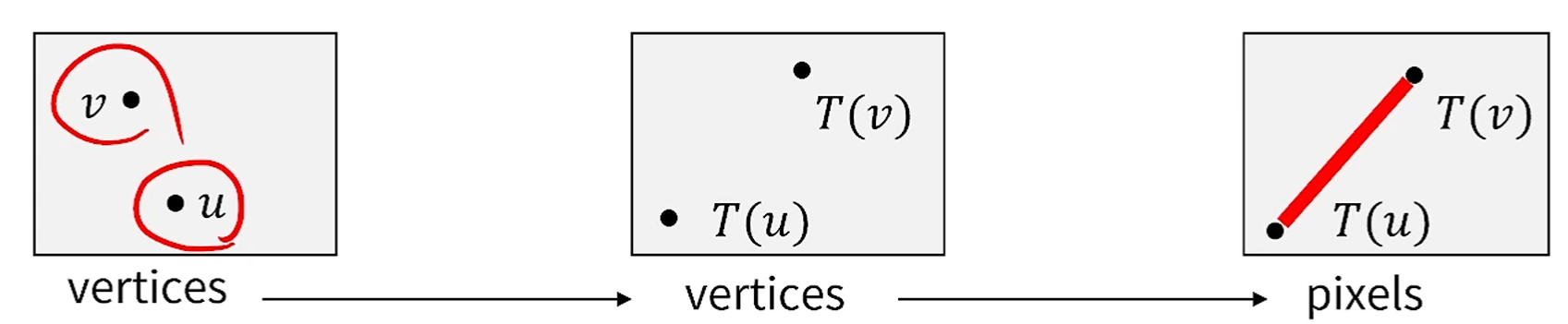
만약 General Transformation이었다면 v->T(v), u->T(u)로 변환될 때,
직선으로 변환된다는 보장이 없기 때문에 일일이 다 보내줘야 합니다.

하지만 affine transformation은 line은 line으로 보전이 되지요.
그런 걱정 할 필요가 없다입니다.

Standard(Affine) Transformations

Translation

Point를 새 위치로 옮기는 것입니다.
$P' = P + d$

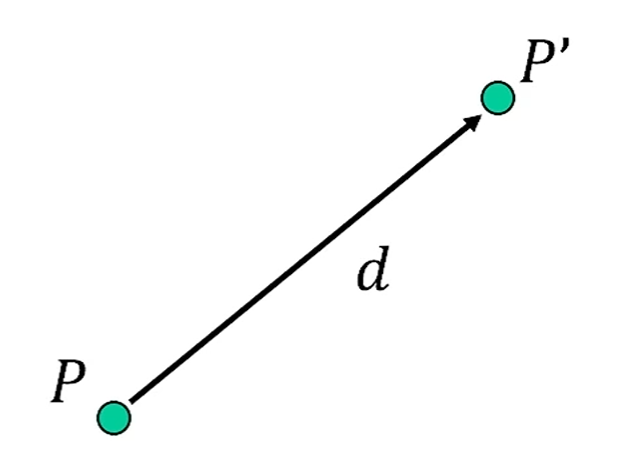
이걸 HC를 이용해 변환해봅시다.

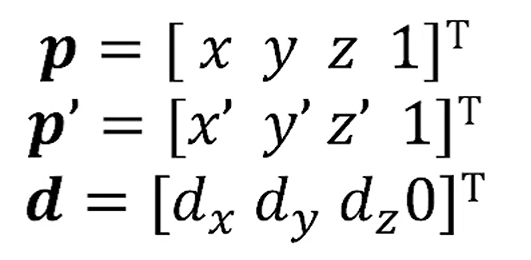
$p, p'$는 점이니까 끝에 1을 넣어야겠죠?
$d$는 vector니까 0일거구요?
그러면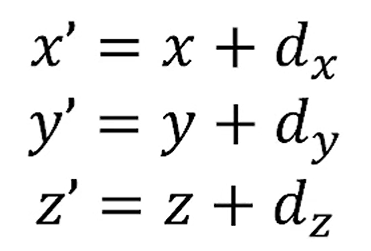

다음이 성립합니다.
쉽죠? 당연해요

우린 이걸 원한게 아닙니다.

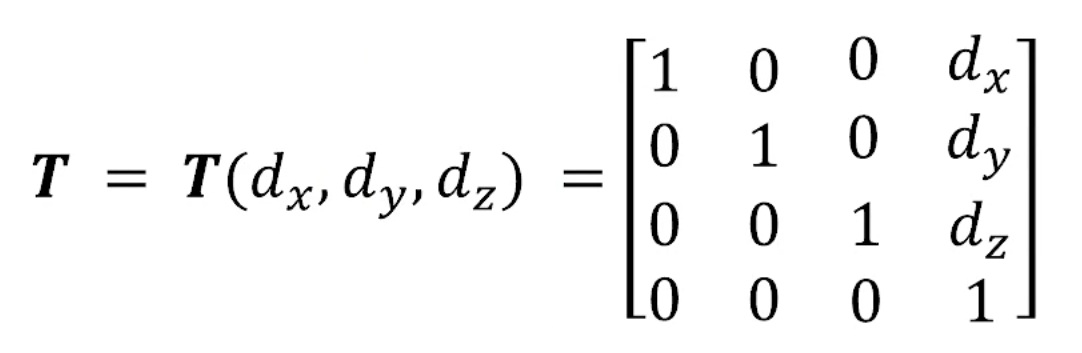
4D로 쓰게 되면, 이렇게 쓸 수 있습니다!

저 T에다가 p를 곱하면 어떻게 된다?
$[x+d_x, y+d_y, z+d_z, 1]^T$이 됩니다. 이게 정말 중요하죠.

왜 굳이 이렇게 하냐.
Translation을 제외한 나머지는 전부 곱셈입니다. 근데 Translation만 덧셈이죠.
그러면 Rotation과 Scaling을 연달아 할 수 있는데, Translation은 그게 불가합니다.

그래서, Translation마저 곱셈으로 바꿔버리면 모든 변환을 연달아서 곱셈으로 할 수 있게 됩니다.

Scaling

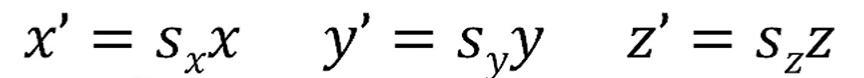
이걸 matrix로 쓰면?

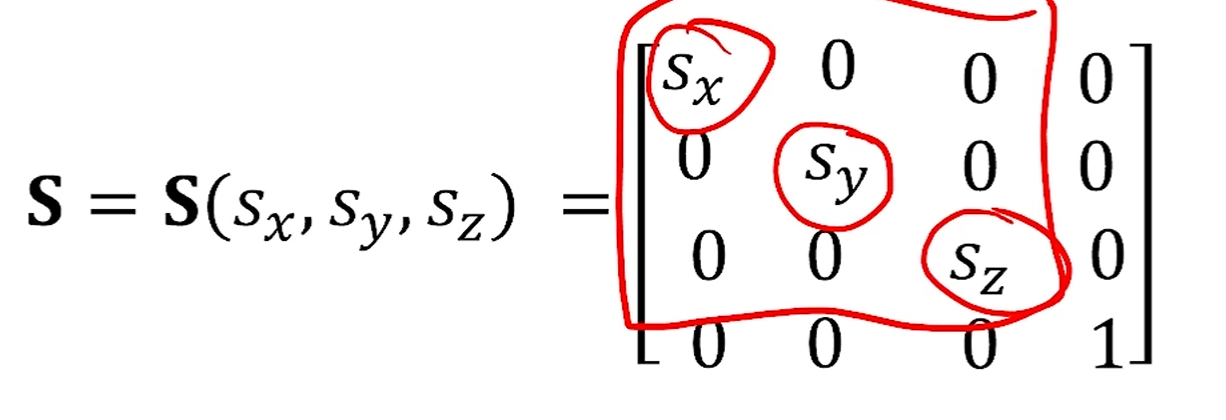
쉽죠.

Rotation

Rotation은 축과 각도가 필요합니다.
축에 대해 점을 몇degree만큼 돌리고 싶은거니까요.

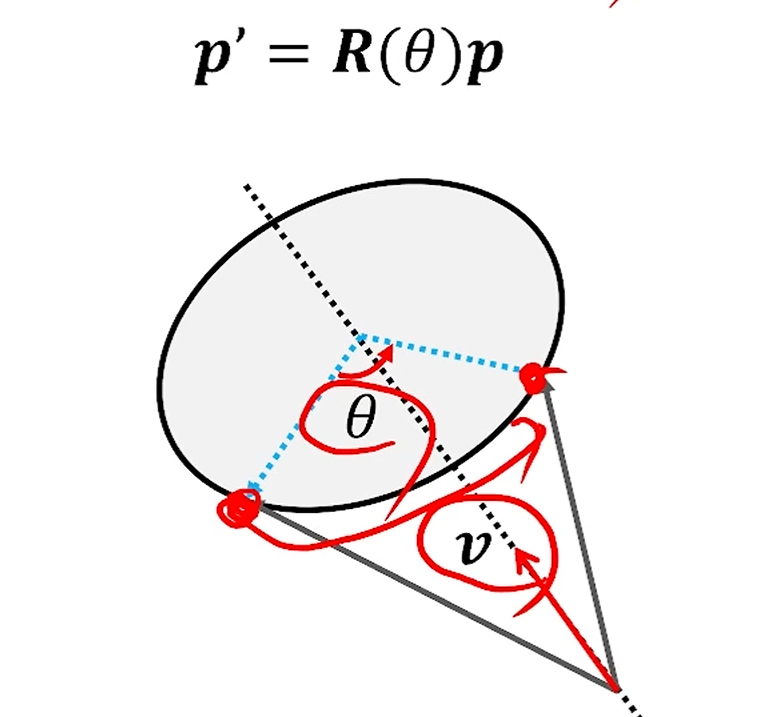
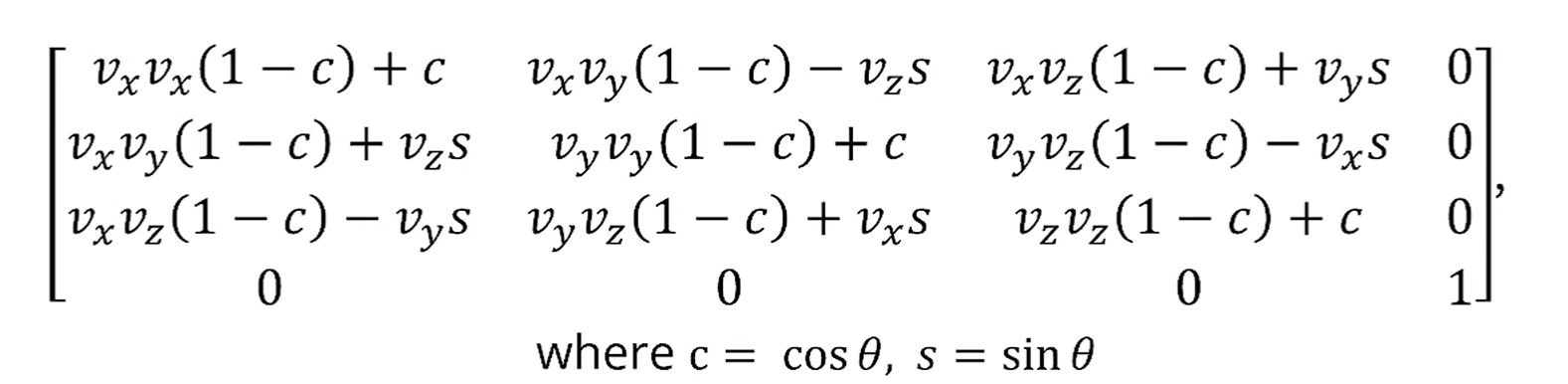
이 때 축 v에 대해 $\theta$만큼 돌리는 rotation matrix는 다음과 같습니다.

여기서 축이 z축이 된다면, rotation matrix는 다음과 같아집니다.

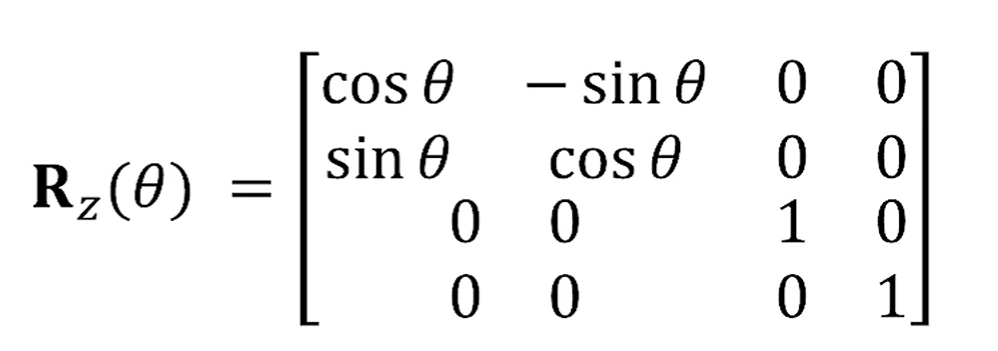
v_x, v_y가 0이 되기 때문이죠.

비슷하게 x축회전, y축회전용 matrix도 유도할 수 있겠죠?

Rotation matrix by Euler Angles

오일러씨가 신기한 걸 발견했습니다.

어떤 Rotation이든 3가지로 분리해서 축 3개에 대한 Rotation으로 쓸 수 있다.

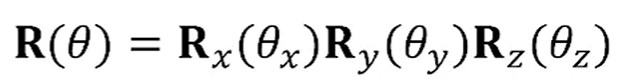
이 때에는 좀 신기한 문제점이 생깁니다.

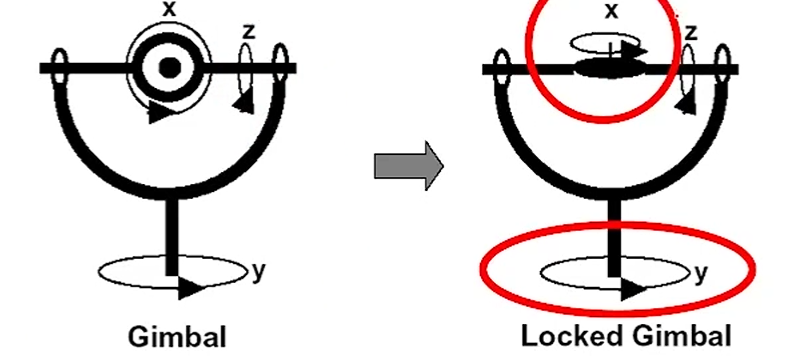
이런 짐벌 구조를 생각할 때, z축으로 잘 회전을 시키면,
x축과 y축이 똑같이 align되는 현상이 생기는데,
이 때에는 x와 y가 동일한 rotation을 가르키기 때문에 degree of freedom을 하나 잃게 됩니다.

문제가 있죠.

Standard 2D Transformation Matrices

2D Application을 개발할 때도 4x4 matrix를 쓰는게 좋습니다.
전부 4x4 기준으로 최적화가 되어 있거든요.

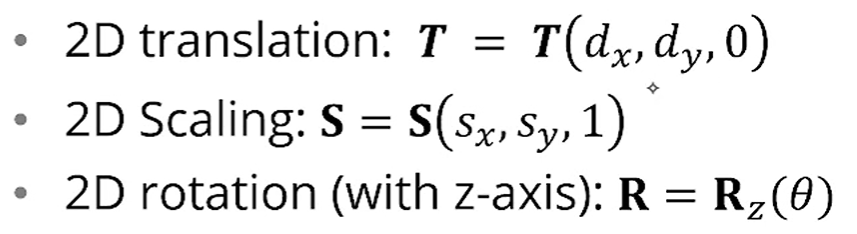
이렇게 넣으면, 2D에서의 translation / scaling / rotation이 가능합니다.

General Affine Transformations

Inverse transformations

보통 Inverse를 구할 때 상당히 어려운 계산이 요구됩니다.
하지만, Affine Transformation에선 그런걸 스킵하고 좀 계산이 쉬워지는데요.

직관적으로 생각하면 됩니다.

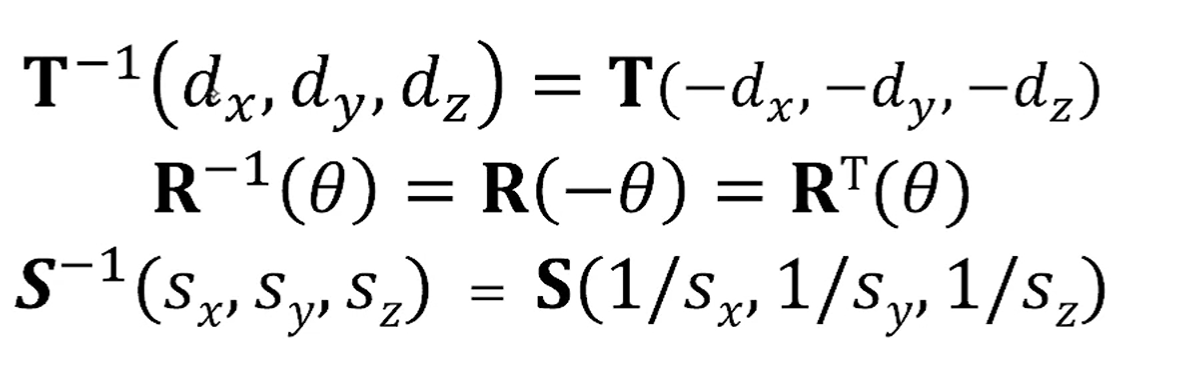
Translation에 대한 inverse는, 그냥 반대로 translation을 시키면 되구요.
Rotation에 대한 inverse는 반대각을 이용하면, $R^T$를 이용해서 scaling을 해주면 되구요.
정확히는 R이 orthonormal한 matrix라서 inverse하면 transpose와 같습니다. (!)

Scaling은 역수를 넣어 scaling해주면 됩니다.

그니까 inverse가 필요할 때 어렵게 inverse를 적용하지 말고,
직관적으로 가면 계산 최적화가 가능하다는 것입니다.

General Affine Transformations

여러 개의 transformation은 어떻게 해야 하냐?
Transformation matrix를 concat 하면 됩니다.

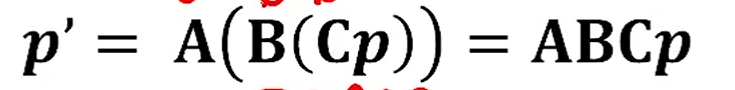
직관적이죠.
근데 matrix 곱의 성질 상 matrix를 미리 곱해놓고 p를 나중에 한번만 곱해도 됩니다.

이게 중요한 성질인게, rigid body (형태 미변환)의 경우는

한번 정의된 vertex의 set들에 대해서,
transformation이 동일하게 들어가기 때문에, ABC를 미리 곱해놓고, 그 후에 p를 곱하면,

원래는 4번 곱한걸 100만만큼 더해야 하는데,
한번만 곱해놓고 100만번만 하면 되니까
vertex당 곱하는 수가 확실히 줄어든다.

이게 중요합니다.

Rotation about Non-origin point

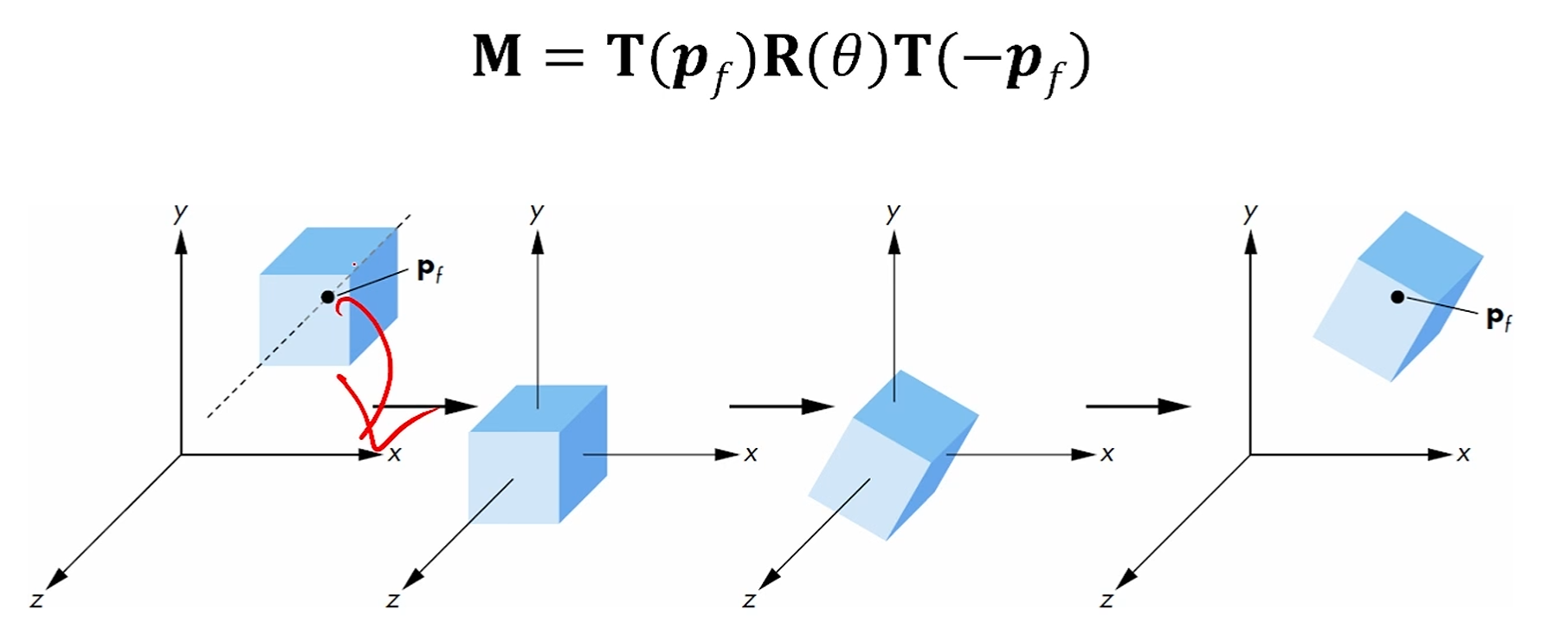
$P_f$를 self-rotate 시키고 싶습니다. z축에 대해서 꼬챙이처럼.

근데 저걸 그냥 돌려버리면 엄청 꼬여요.
왜냐면 지금 Translation 된 상태거든요.

그래서, 원점으로 P_f를 보내고,
원점에서 rotation을 하고,
다시 옮겨오는 방식을 사용합니다.

Instancing

model이 같은데, 그 model을 여러 번 쓰고 싶을 때,
model을 원점에 두고 만들고,
거기서 scaling을 하고, rotation을 하고, 보낼 위치로 translation을 합니다.

SRT 순서. (그럼 곱해질 땐 TRS)

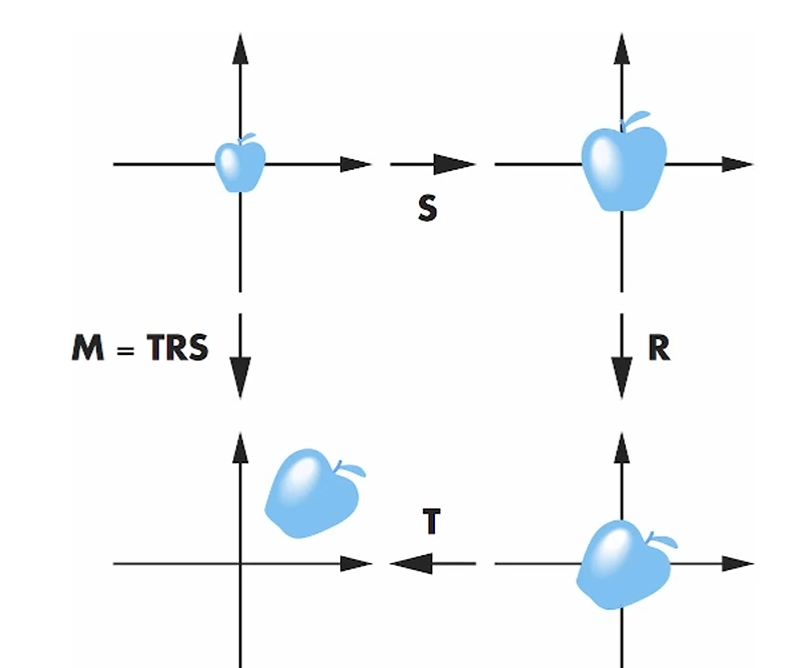
Transformation이 concatenation이 되기 때문에,
이렇게 instancing으로 model을 여러 개 찍어낼 수 있습니다.