6. Projection

앞서 잠깐 언급만 됐던 Orthographic Projection과 Perspective Projection에 대해 자세히 알아봅시다.

Coordinate System

Camera Convention in OpenGL

OpenGL에서, 카메라는 오른손법칙을 따라서,

z축이 내 얼굴 쪽을 바라보게 설치가 됩니다.

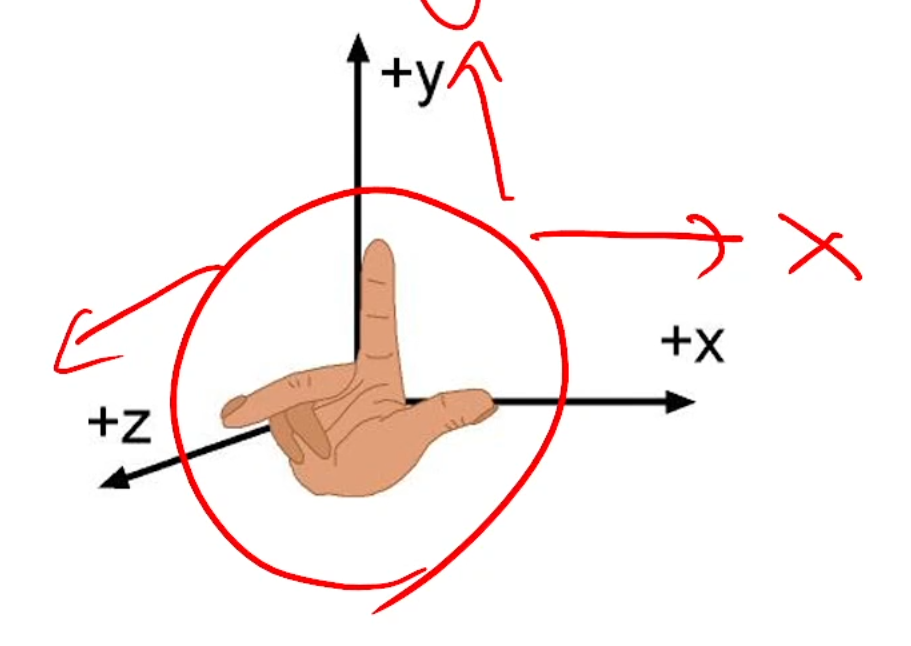
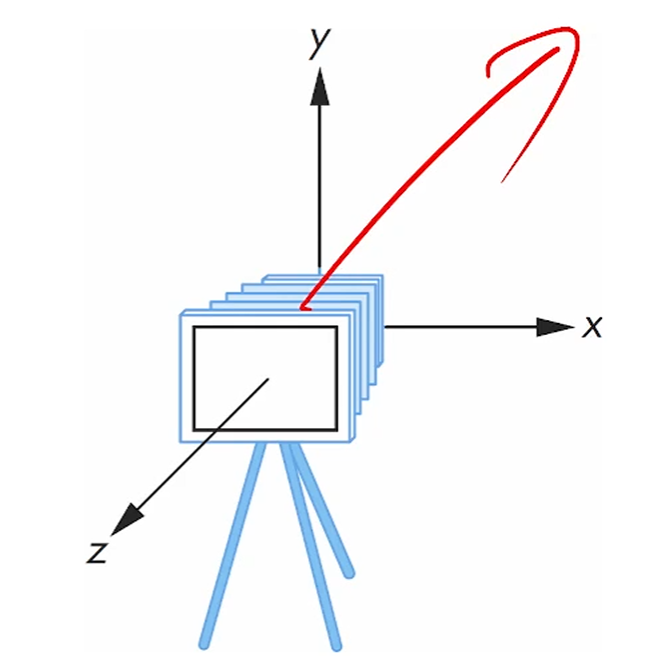
즉, 카메라의 렌즈는 -z 방향을 바라보는거죠.

Normalized Device Coordinate (NDC)

Projection이 끝난 다음에 쓰는 Coordinate System.
정규화를 해야 3D 화면의 점을 2D 화면으로 출력할 수 있기 때문에,
NDC를 사용합니다.

얘는 LHS Convention을 씁니다.
z가 큰 값이 멀리 있는 놈이 됩니다.

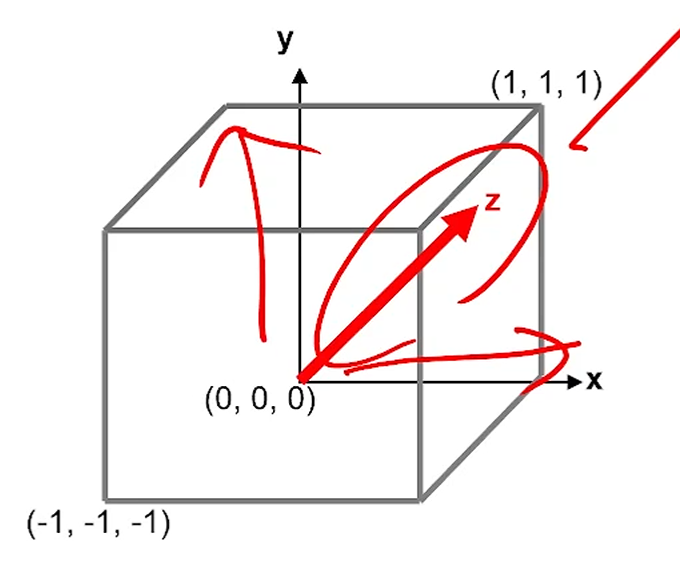
좀 더 직관적으로 알아볼 수 있게 이렇게 바꾸는거죠.
왼손 중지가 z방향이 가게끔 하면, 엄지가 x입니다.

Parallel Projection

COP를 무한대로 보냈을 때 DOP가 됐었죠.

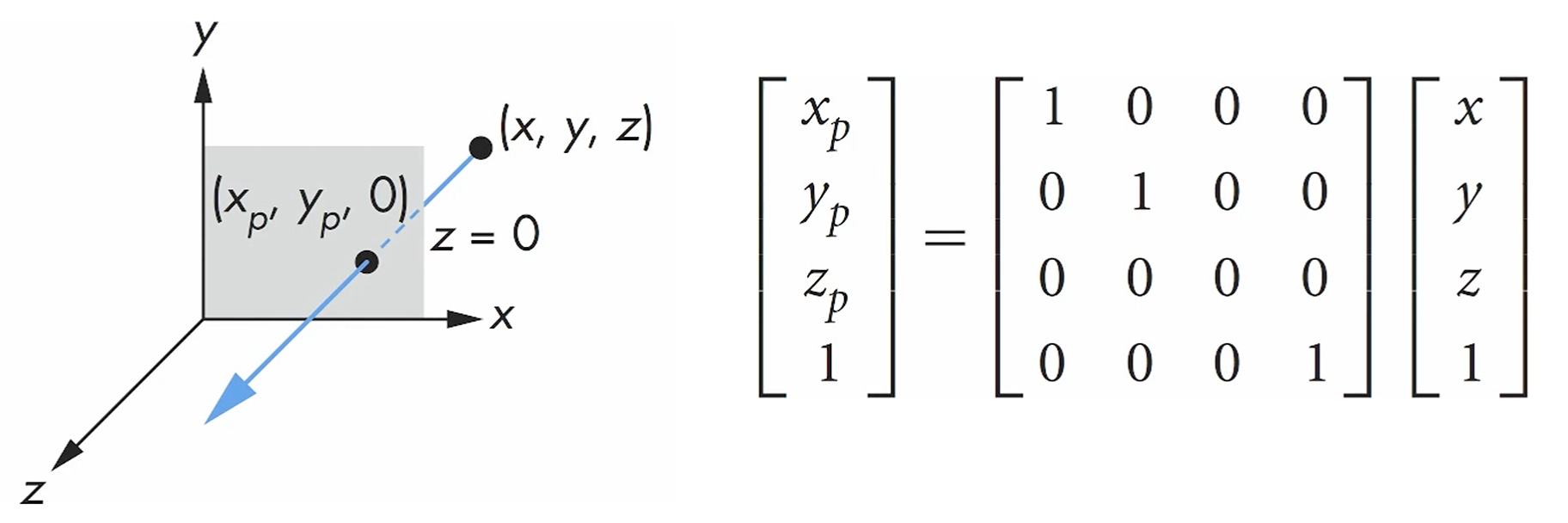
(x,y,z)를 xy plane에 projection 시키기 때문에, z = 0으로 두면 projection이 끝납니다.

단순한 matrix를 곱하면 projection이 구현되죠.

근데 이렇게 projection 하면 z가 날아가고, depth test를 할 수가 없습니다.

그래서, OpenGL에선 view volume normalization을 같이 진행합니다.

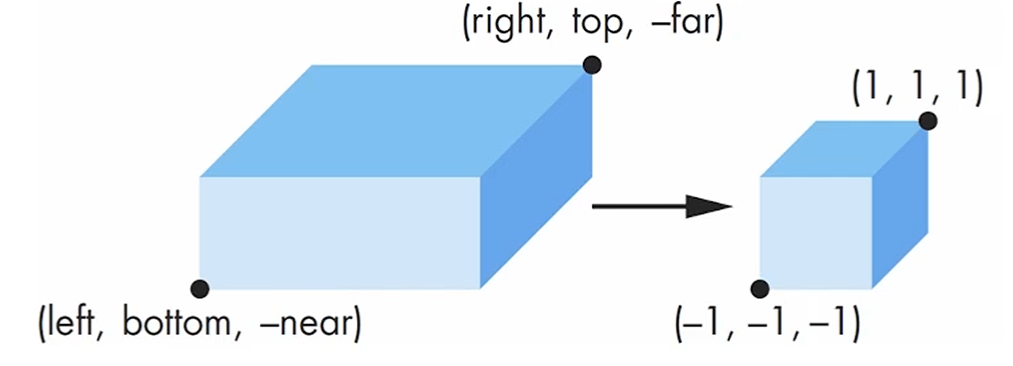
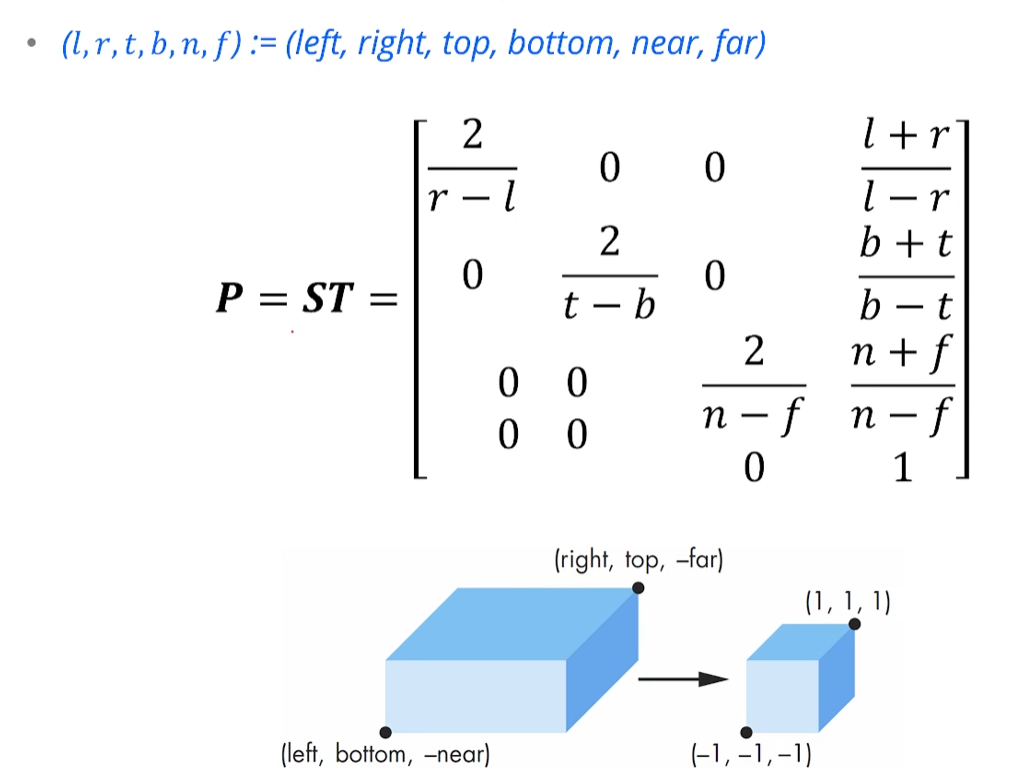
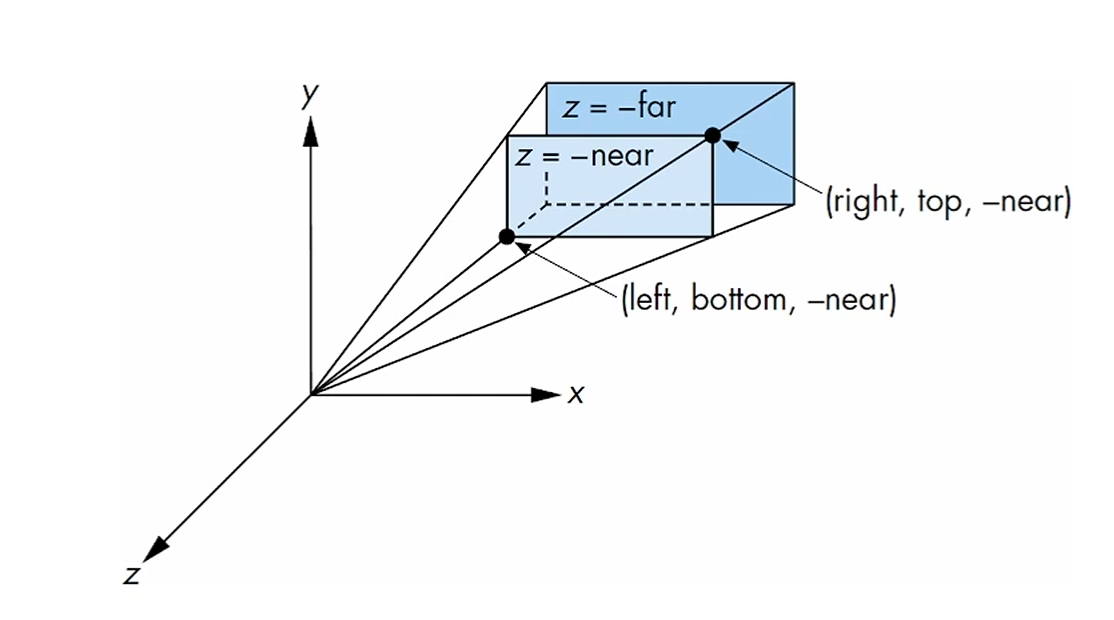
6개의 parameter를 갖고 정의되는 orthographic projection의 view volume이,
변의 길이가 1인 cube로 normalize됩니다.

이걸 view volume normalization이라고 합니다.

사용자가 정의한 (left,bottom,-near) 에서 (right, top, -far)까지의 공간에서
길이가 2인 정육면체인 NDC로 normalize하는게 view volume normalize죠.

이 때, depth를 살리기 위해서, orthographic projection을 진행하면서도,
z 값은 남겨둡니다.

그래서 depth test를 할 수 있게 되죠.

VVN의 또 다른 장점은, clipping이 쉬워짐입니다.
Z가 [-1,1] 사이에 없다면 잘라버리면 됩니다.

그래서 이 Orthographic projection을 위해서는,

이 mat4를 구해야겠죠?

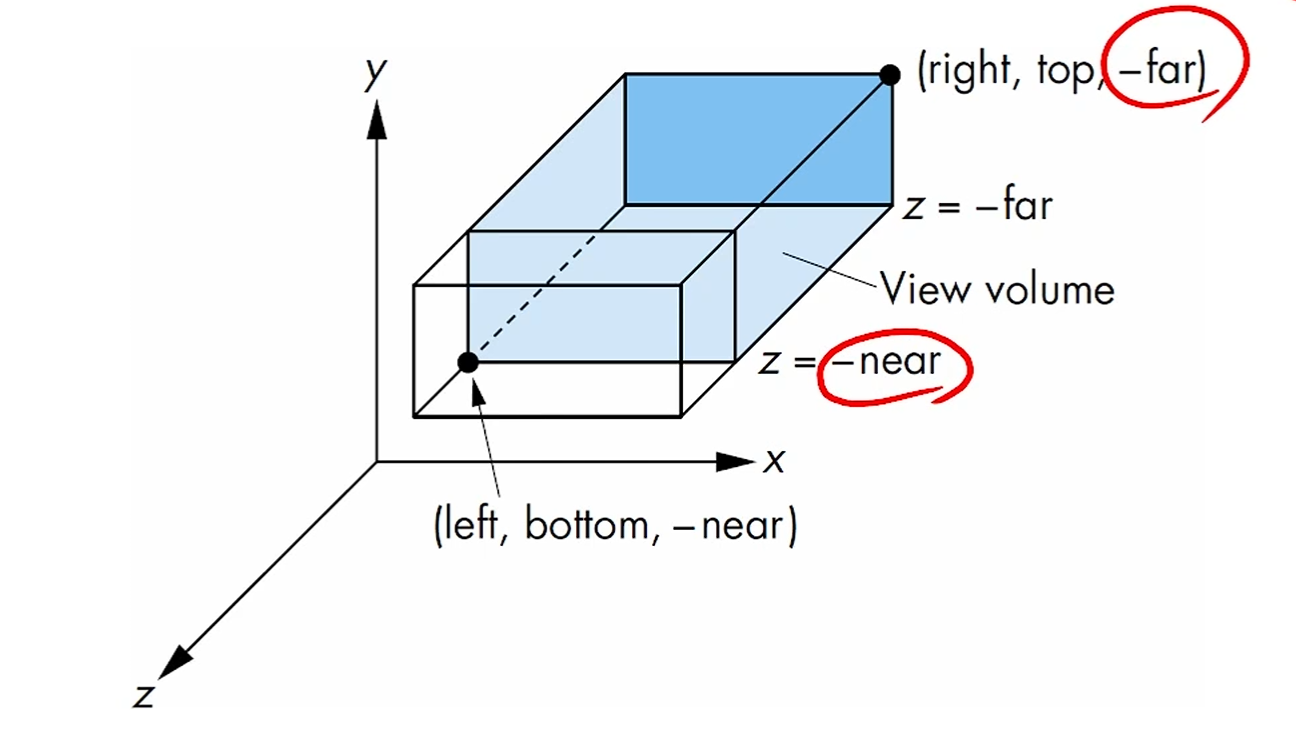
실제 좌표계 상에서의 near와 far가 -near고 -far임에 유의합시다.

OpenGL에선 RHS를 쓴댔죠?
그래서 카메라가 보는 방향이 -z 방향입니다.

아무튼 저 View Volume을 NDC로 변환하기 위해선,

View Volume의 원점을 NDC의 원점으로 옮긴 후,
Scaling하면 되겠죠.

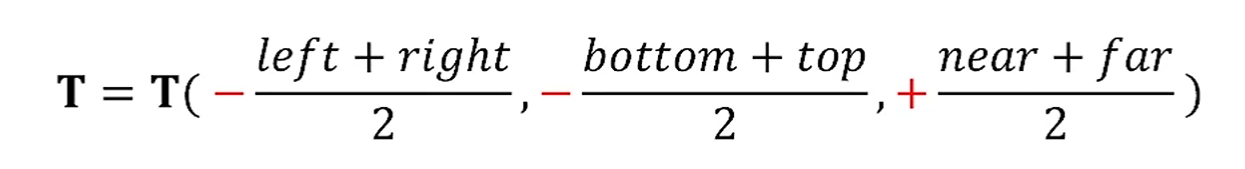
우선 이 Translation matrix를 적용하여 원점을 일치시킵니다.

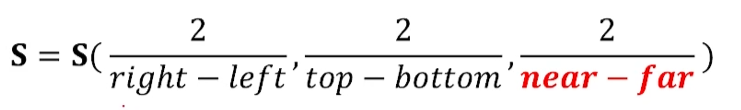
그 다음 이 Scaling Matrix를 이용하여 scale을 변환합니다.
이 비율을 이용하면 길이가 몇이든 2로 변환이 가능하죠.

여기서 핵심은 near보다 far가 z값이 작기때문에 near - far를 해줘야 한다는 점.

그걸 다 정리하면 다음과 같아집니다.

Simple Perspective Projection Matrix

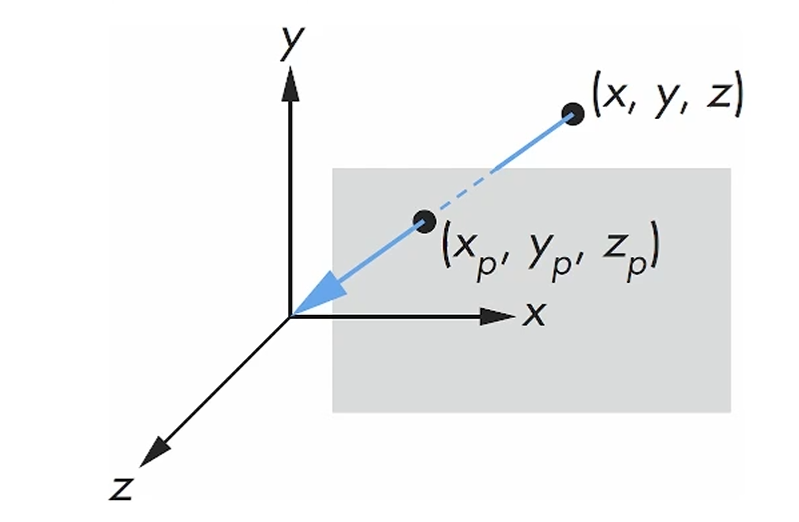
이런 단순한 투영 먼저 생각합시다.
COP로 향하는 (x,y,z)가 plane과 붙는 그 점이 투영점입니다.

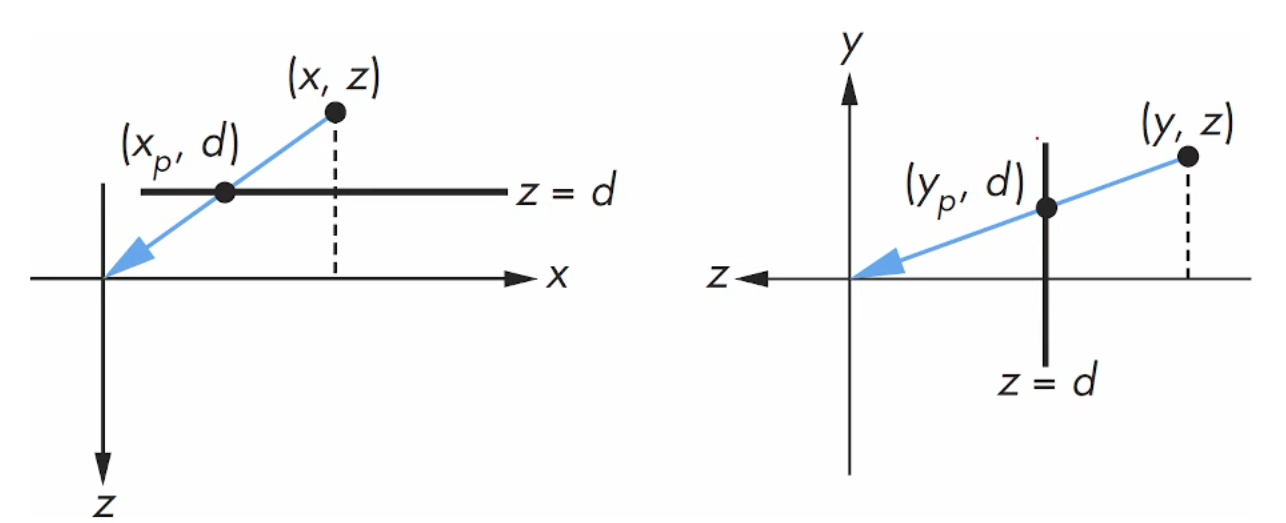
수학적으로 그려봤을 때, d < 0이고,
$x_p = \frac{x}{z/d}$, $y_p = \frac{y}{z/d}$를 구할 수 있습니다.

이걸 다시 4x4 matrix로 바꾸면,

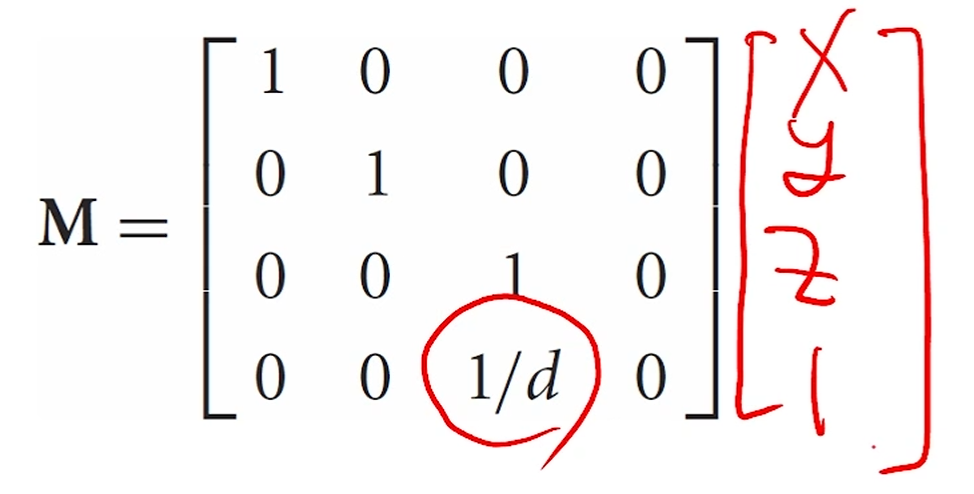
다음 초간단한 matrix만 이용해도 $[x,y,z,z/d]$가 만들어져서,
HC에서 Cartesian으로 옮길 때 w값이 1이 아닌 경우 나누면 되기 때문에,
$[x/(z/d), y/(z/d), d, 1]$이 됩니다. 세상에!

Symmetric Perspective Projection Matrix

조금 더 어려운걸 해봅시다.

마찬가지로, Simple Perspective Projection에 View Volume Normalization을 진행합니다.

이번엔 orthographic space와 다르게 (right,top,-near)가 한쪽 끝이 되죠.

이번엔 뜀틀 모양(frustrum)을 정육면체로 압축하는게 목표입니다

우선, 다음 형태로 정의된 x,y를 -+z로 scaling해줘야 합니다.

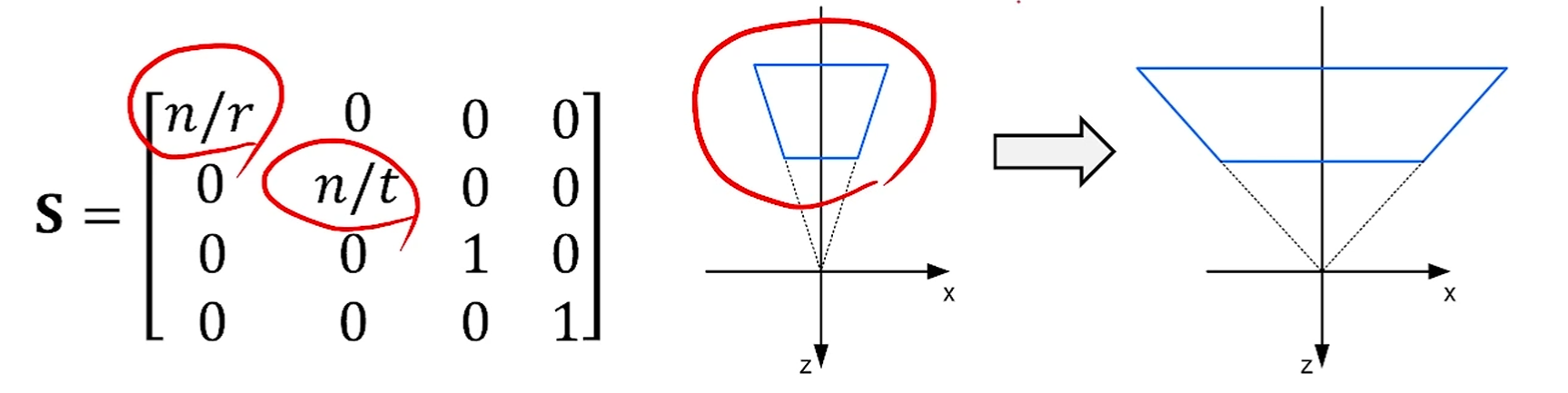
그러면, 이렇게 x랑 y만 '기울기가 1'로 scaling하는 matrix를 얻을 수 있습니다.

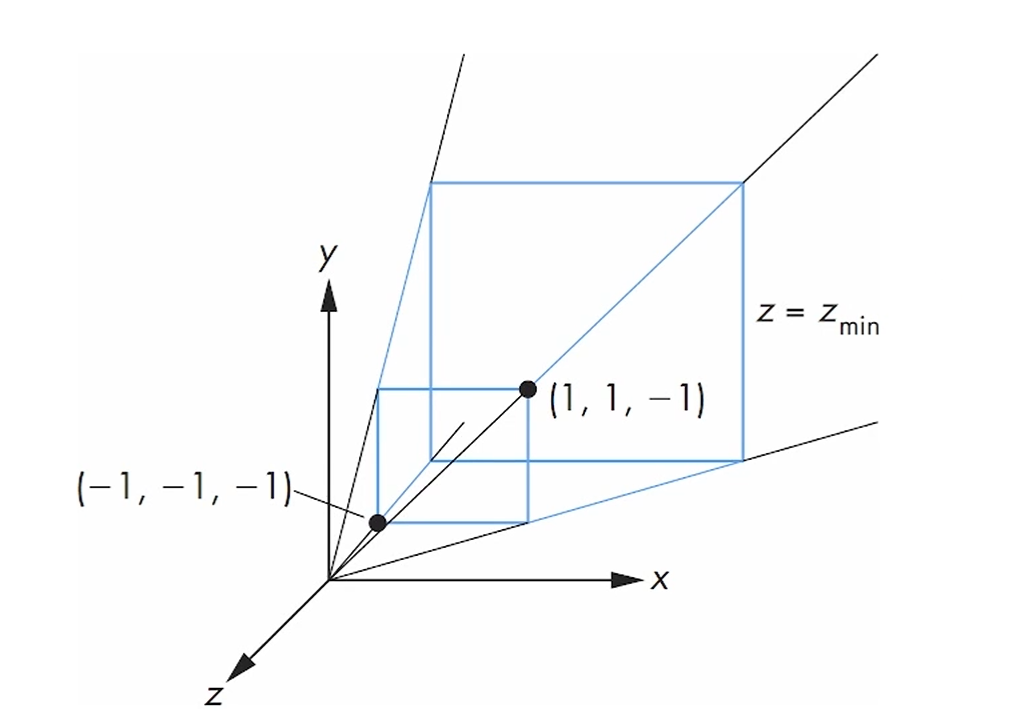
두번째 단계로, near clipping plane을 z = -1에 두고,
depth가 범위로 projection이 되게 바꿔주는 단계가 있습니다.

우린 최대한 가까운걸 -1로, 먼걸 1로 매핑해야 하기 때문에,
-near -> -1, -far -> 1로 매핑해줍니다.

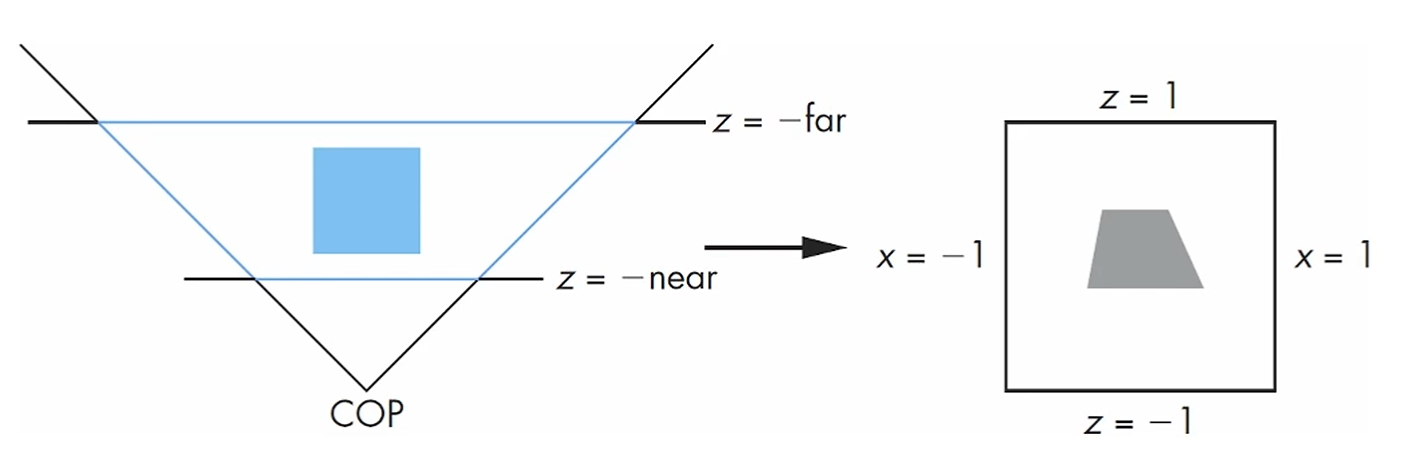
대충 이렇게 만들어지면 되겠죠?

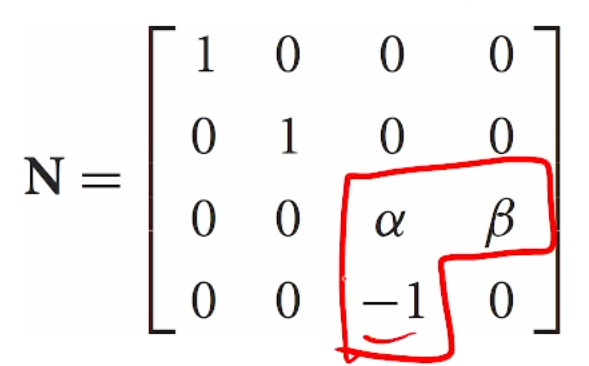
이게 Perspective Projection Matrix의 형태입니다.

밑의 -1은 near를 -1로 잡았기 때문이고,
a랑 b는 길이 조절 계수입니다.

해당 matrix를 적용하면,

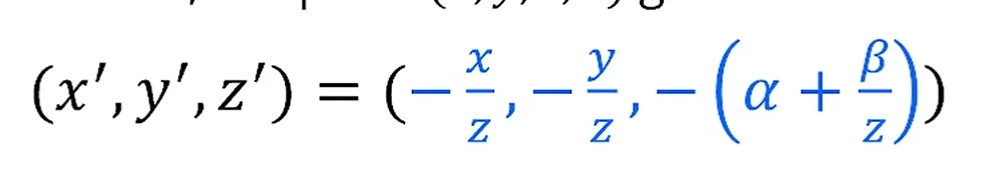
이렇게 변환되는데,
앞서 $x = \mp z$, $y = \mp z$로 normalize했기 때문에,

저 depth인 $-(\alpha+\frac{\beta}{z})$만 -1~1 사이로 매핑을 시켜준다면,

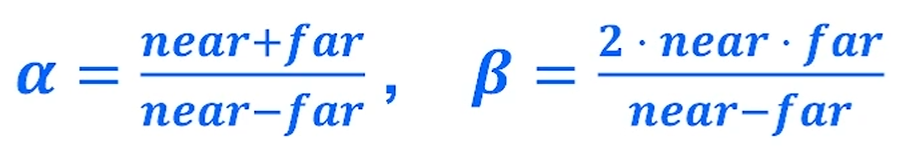
이렇게 나옵니다!

그걸 이제 앞서 Scaling을 먼저 적용한 Scaling Matrix에 합치낟면,

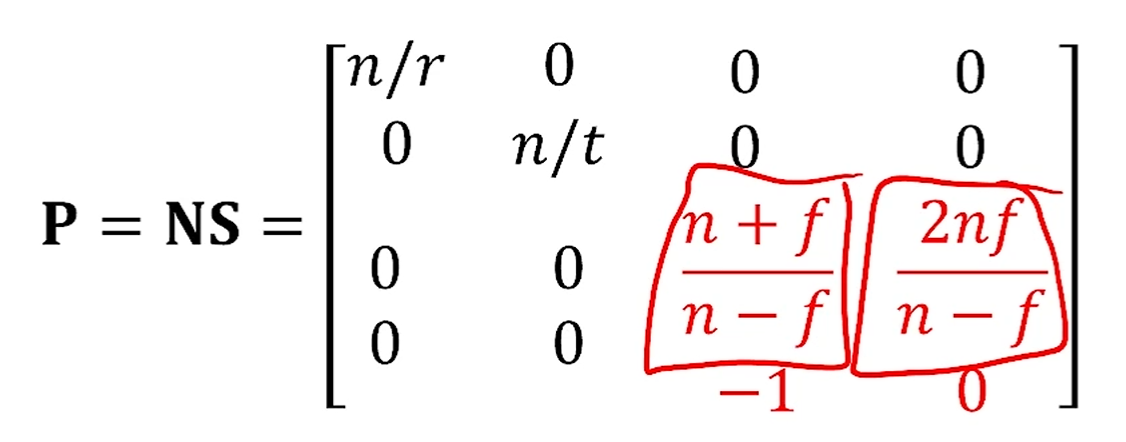
이 P가 최종적으로 Symmetric Perspective Projection Matrix가 되네요.

문제는, r과 t를 재려면, 거리에 따라 r과 t가 달라집니다.

그래서 카메라를 움직일때마다 저걸 정해준다..?

Perspective()

직관적이고, controllable한 parameter를 이용한 perspective matrix입니다.

화각 (fovy)와 width/heigth비율 (aspect_ratio)를 이용하여 정의하는 함수입니다.

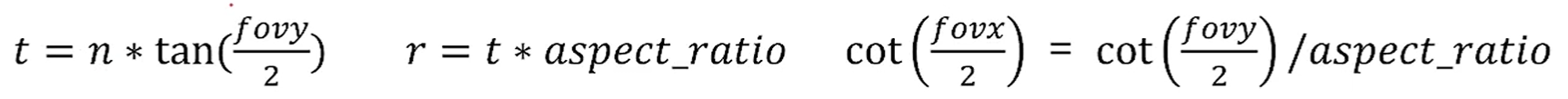
이 때 다음과 같이 t, r을 정의할 수 있습니다.
(간단한 삼각비입니다.)

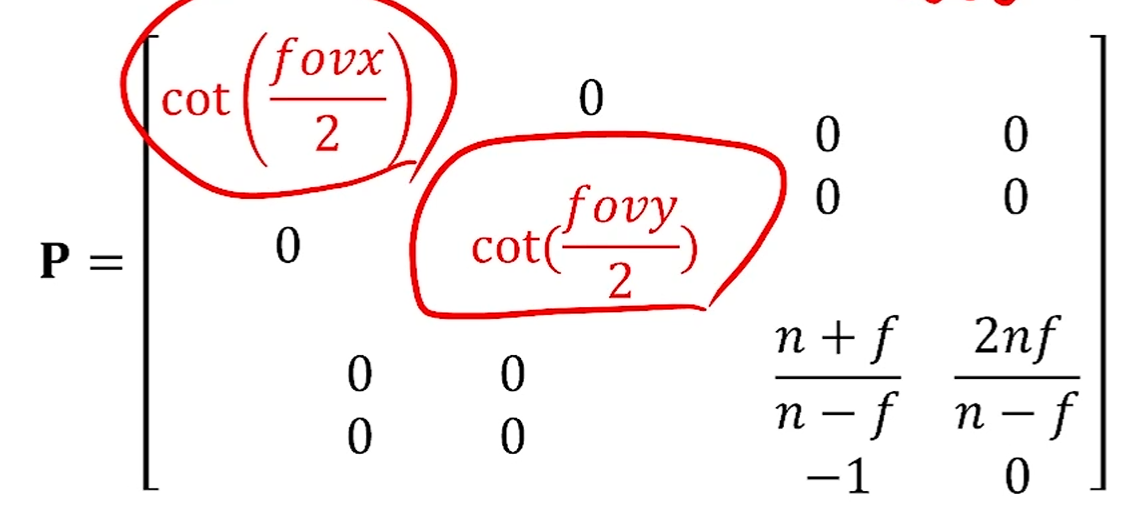
이제, Frustrum을 잴 때, lrbtnf를 일일이 다 재서 함수에 넣을 필요가 없구요.

화각과 aspect만 정해주면 matrix를 쉽게 알 수 있게 됩니다.

Non-Symmetric Perspective Projection

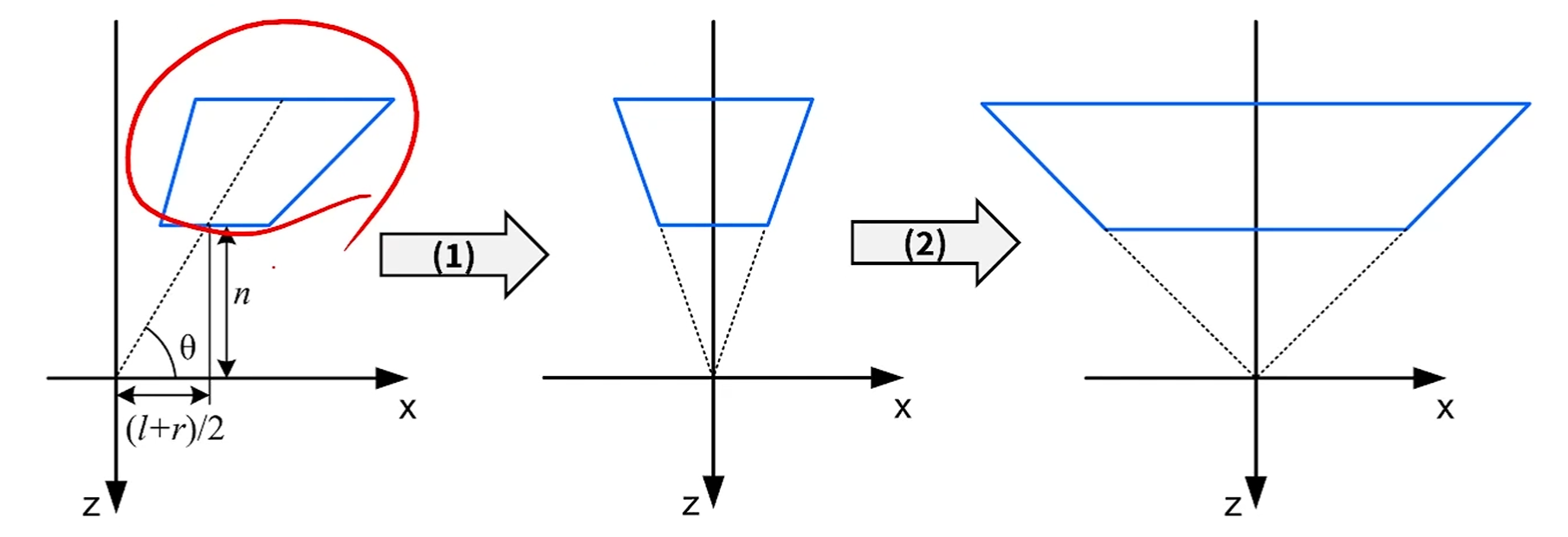
이런 못생긴 frustrum을 shear 해서 예쁘게 만들어주고, 똑같은 기법을 취하면 됩니다.

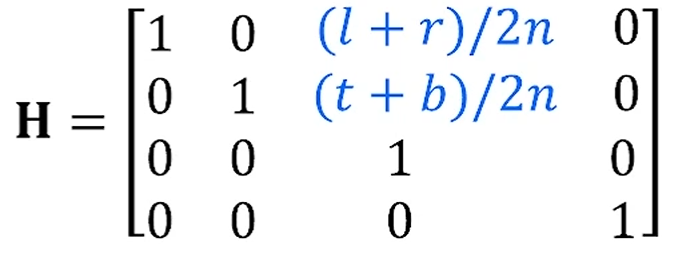
수학적으로 그 Shear Matrix는 다음과 같습니다.

그렇게 Shear까지 한 General한 값은,

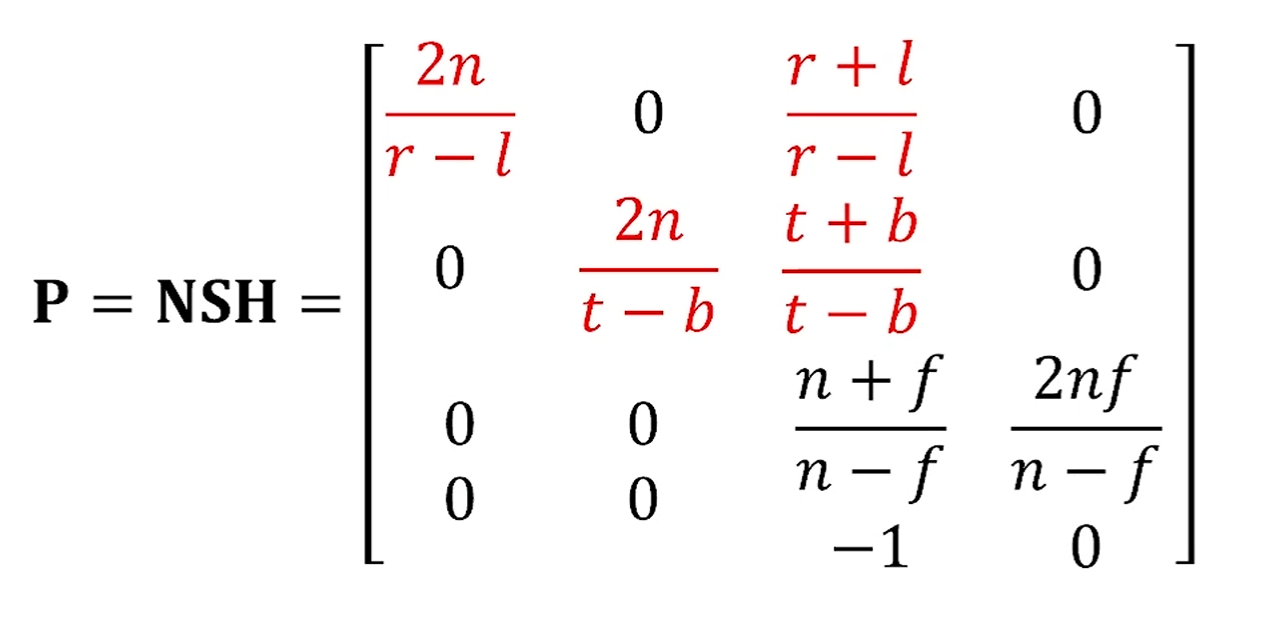
다음과 같습니다.