5. Viewing

4 Elements of Viewing

• Objects
• Viewer
  Viewer는 Projection되는 그 Center라서, COP (Center Of Projection)이라고도 불립니다.
  

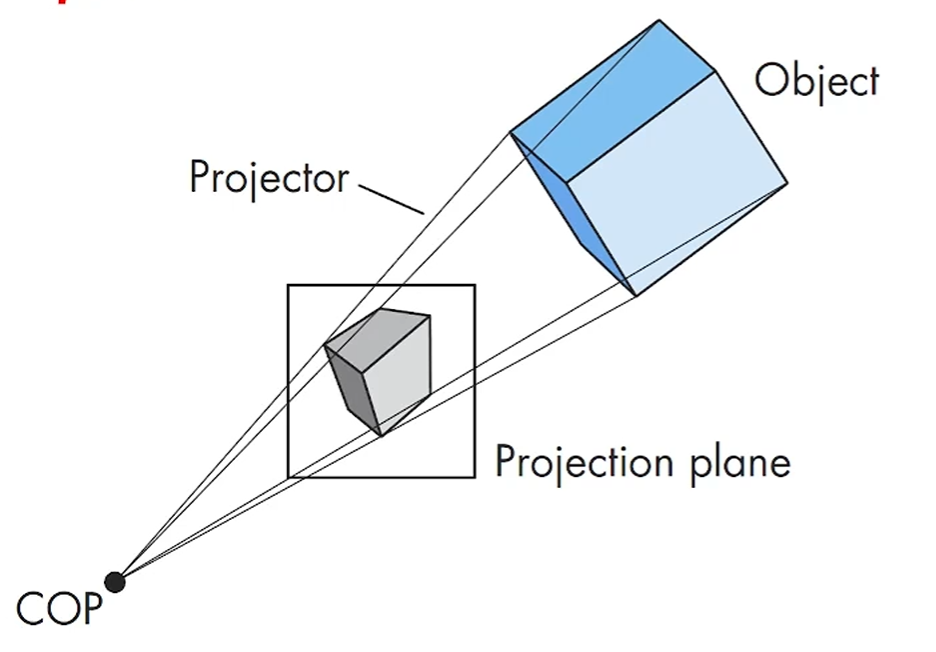
즉 Camera View를 정의할 때, 원점은 COP가 되구요.
카메라 좌표계에서 (0,0,0)에 해당합니다.

• Projection Surface
  우린 Plane을 하나 잡고, Object를 거기에 Projection할 겁니다.

• Projector
  Projection을 carry하는 line들.
  Object에서 COP로 떨어지는 저 line들이 Projector입니다.

Parallel Projection

COP가 무한대로 향하면 어떻게 되나요?
그러면 Projector들은 평행해지겠죠?

그 경우 COP 대신, DOP (Direction Of Projection)이라고 부릅니다.

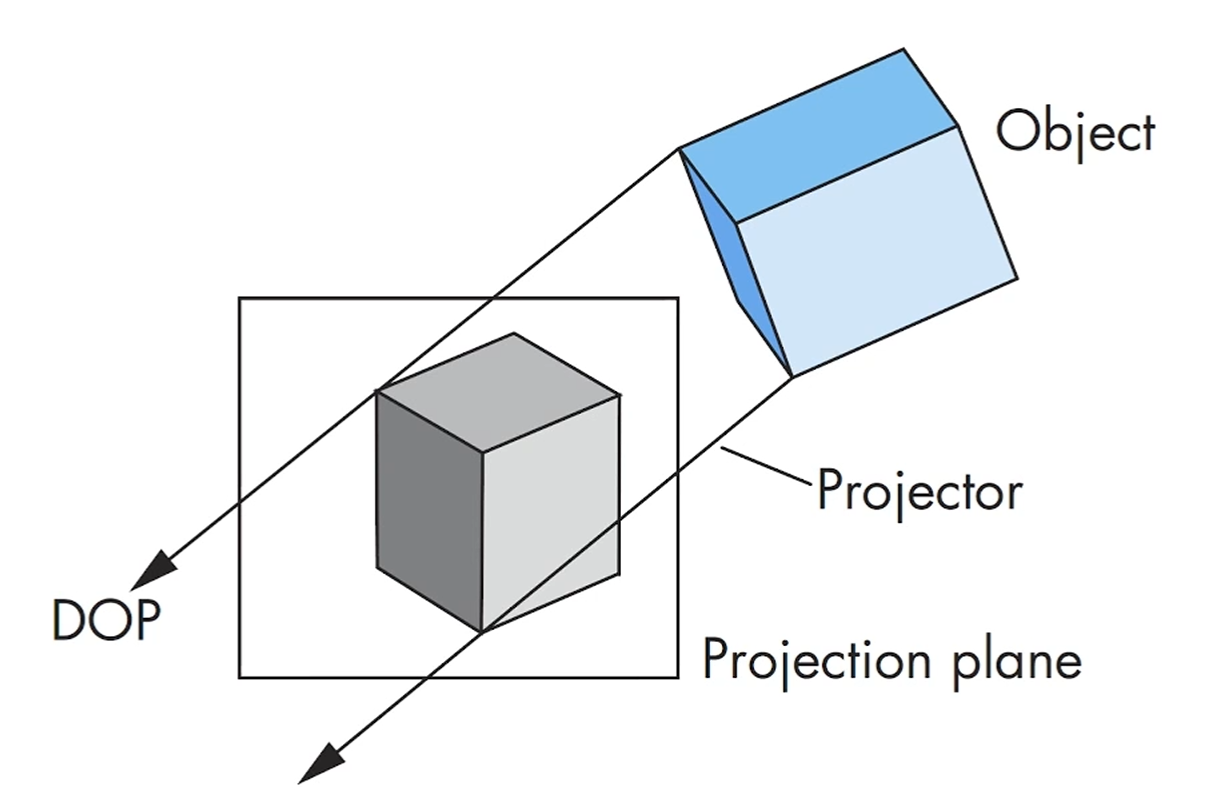
Orthographic Projection

Projector가 Projection Surface에 수직하다면,
Orthographic Projection이라고 부르고, 2D Viewing에 많이 쓰입니다.

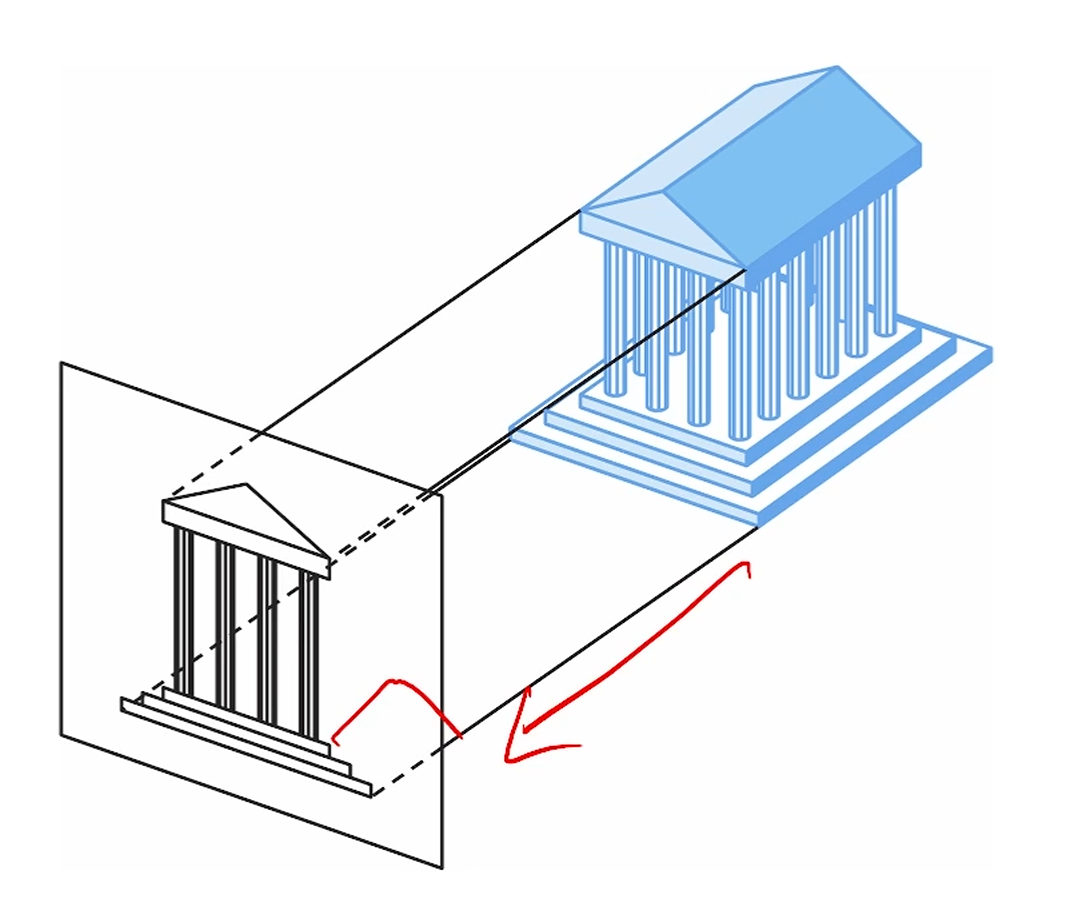
보통 모델링할 때 CAD같은 곳에서 많이 씁니다.

Perspective Viewing

우리의 실제 관점을 중요하게 보는 Perspective Viewing에서는,
diminuition, 즉 멀리 있을 수록 작게 보이는 것을 중요한 특징으로 갖습니다.

사람 눈이나 카메라로 볼 때의 기본적인 특성이 되지요.

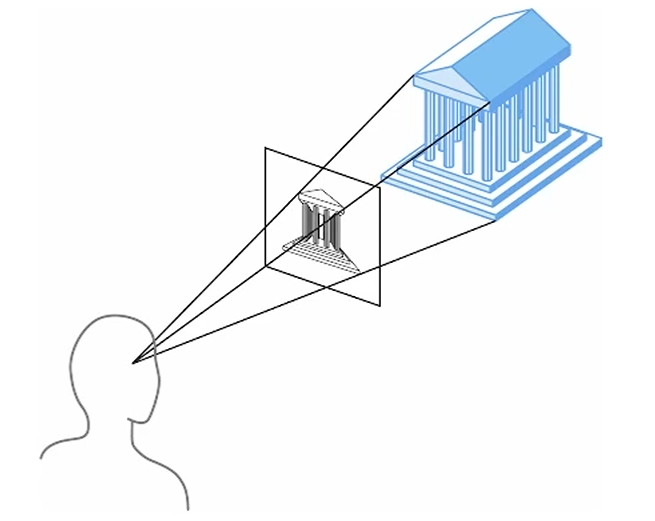
이렇게 줄어드는 정도에 따라서 어느게 멀리있고 어느게 가깝게 있는지에 대한 정보도 줄 수 있지요.

Computer Viewing - 2 viewing approaches

Computer가 쓰는 2가지 Viewing Approach가 있습니다.

Backward Approach

CPU에서 ray-tracing을 할 때 씁니다.

보통 카메라로 빛이 들어가는데, 이건 반대로 카메라 에서 빛을 쏩니다.

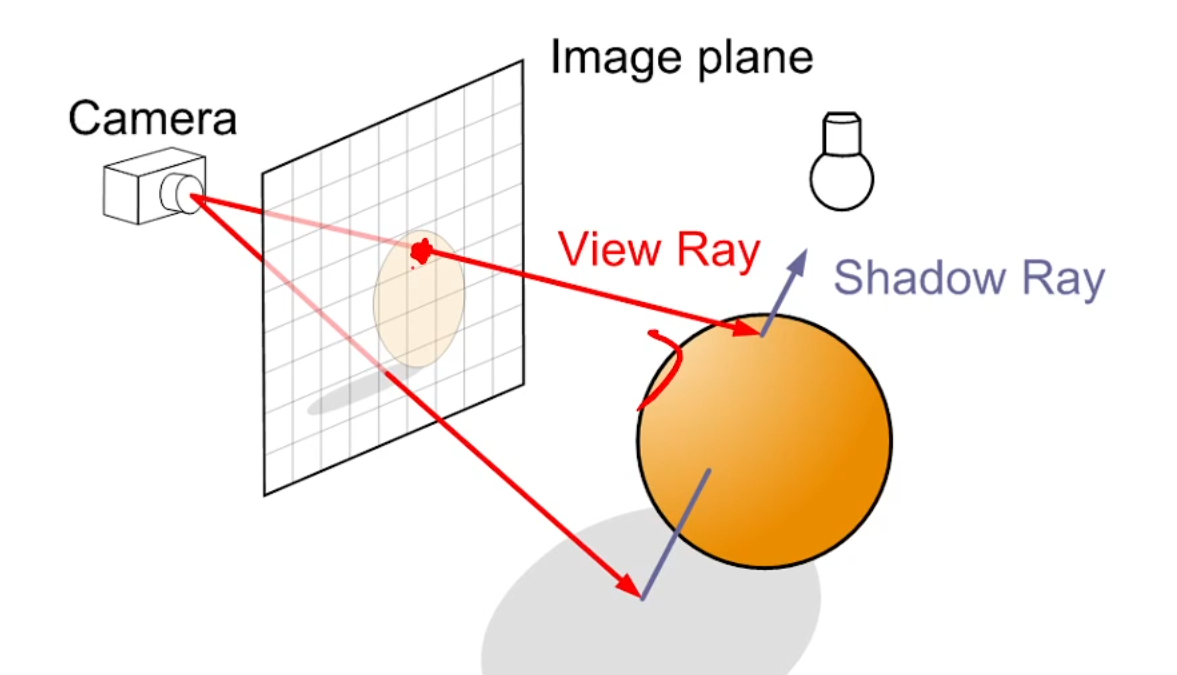
카메라에서 일단 Plane쪽으로 Ray를 쏴서, (View Ray)
View Ray를 맞으면 반사를 시키고,

Shadow Ray를 또 추가로 쏴서,
Shadow Ray를 맞은 곳에서 광원 쪽으로 Ray를 쏴서 만약 blocking이 되면,
Shadow 내에 있다고 간주하고 Shadow를 제작합니다.

Forward Approach

빛이 오는 방향과 같은 방향으로 object에서 빛이 들어옵니다.

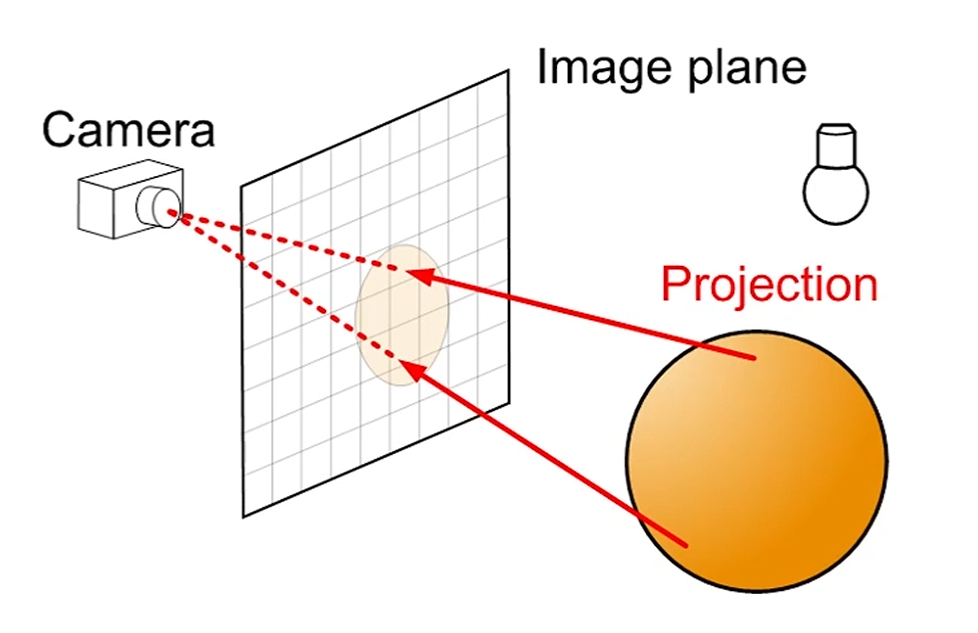
interactive application들은 Forward Approach가 기본입니다.

물체와 광원 사이의 관계를 고려해 색깔이 만들어지고,
그게 그대로 들어옵니다.

이게 Pipeline approach라서, matrix곱으로 구현이 됩니다.

전부 여러 번의 Transformation으로 구현이 됩니다.

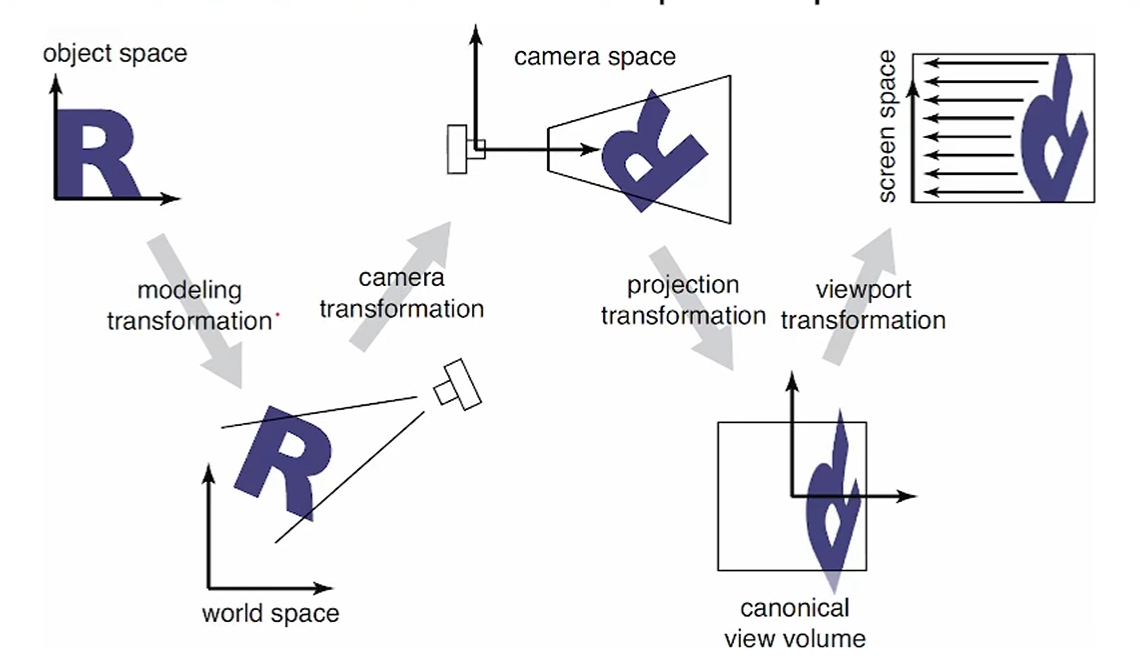
전부 4x4 matrix를 써서 유도합니다.
자세한건 추후 배웁시다.

Lookat Matrix

우리가 어떤 object를 보여줘야 한다면, 2가지 방법이 있는데요.

카메라를 움직이는 것과,
카메라 반대 방향으로 object를 움직이는 것이 있습니다.

그리고 2번째 것이 더 편합니다. (?)

이걸 Model-View Duality라고 부릅니다.

카메라를 Camera Space에서 고정시키는 거죠.

LookAt Method

mat4 look_at(eye, at, up)

가장 유명하고 기본적인 method입니다.
Camera는 항상 origin에 고정하고,
object를 inverse matmul을 이용해 보내는 형태를 취합니다.

View를 지정하려면, eye, at, up 이 3가지의 parameter가 필요합니다.

eye : Camera의 World에서의 location
at : 보려고 하는 것의 위치
up : Camera의 위쪽을 가르키는 Vector

이렇게 3가지 eye, at, up이 있으면
카메라 Frame을 지정할 수 있습니다.

Frame은 3개의 basis vector와 1개의 원점 point가 있어야 하는 것 아닌가요?

point는 카메라의 원점, 즉 eye가 되구요.

eye, at, up을 잘 조합하면 basis 3개가 나옵니다.

n = normalize(eye - at)
u = normalize(up x n)
v = normalize(n x u)

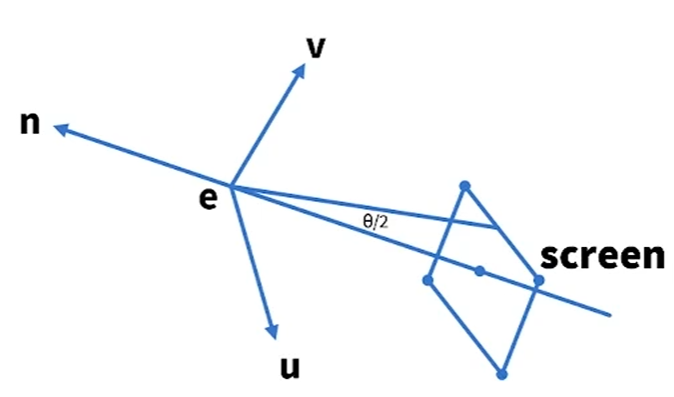
basis이기때문에 normalize는 필수입니다.

이제 u,v,n을 x,y,z처럼 사용하면 됩니다.

아무튼 이제 frame을 만들었죠?
이제 frame간의 변환도 가능합니다. 그 변환을 Lookat matrix로 합니다.

world frame에서 camera frame으로요.

Building Lookat matrix as Change of Frame

우린 x,y,z와 (0,0,0)을 u,v,n과 eye로 옮겨올겁니다.

첫번째로 할 일은
world frame을 camera frame 반대방향으로 이동시키기입니다.
(Model-view duality)

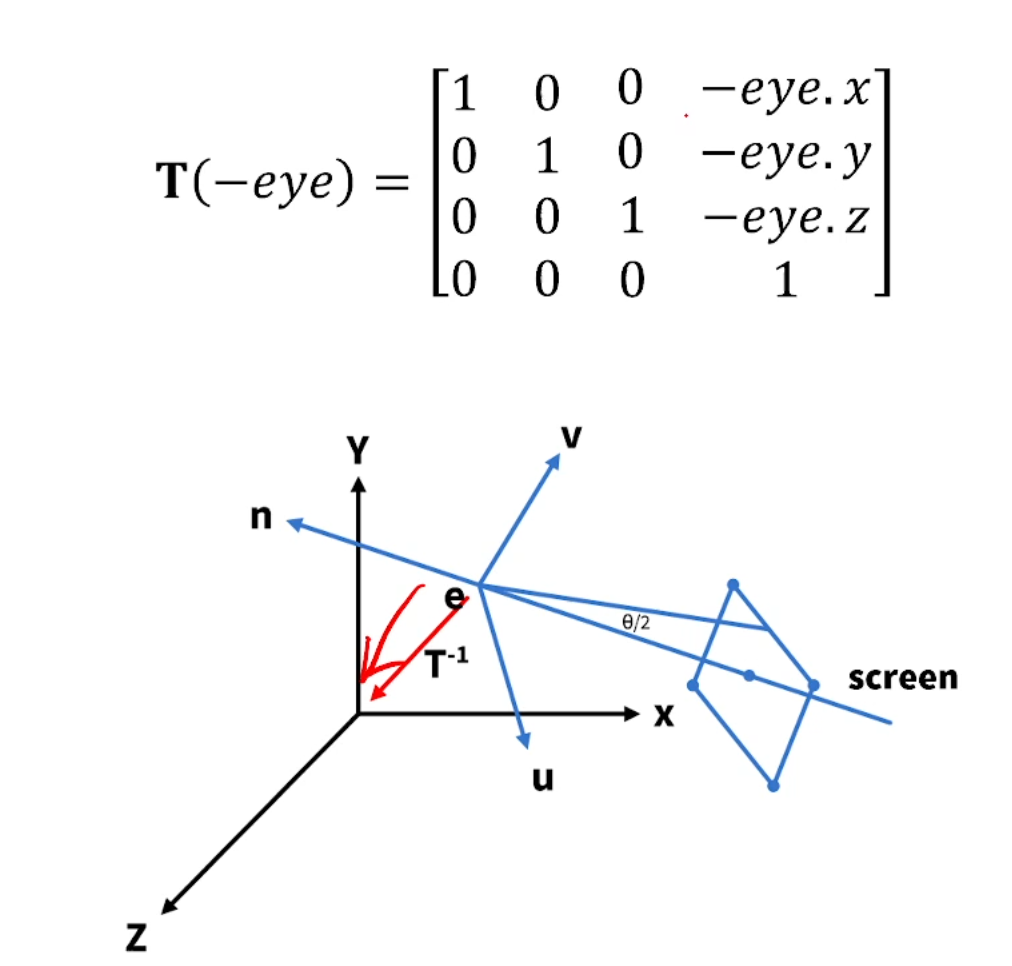
두 번째로 할 일은, 이제 basis vector들을 rotation을 통해 일치시켜 줍니다.

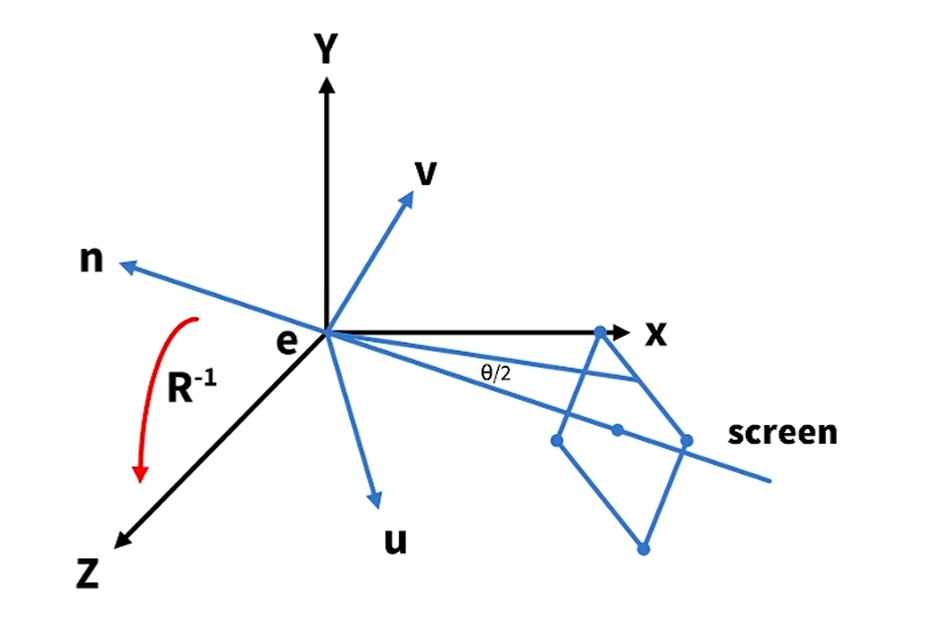
rotation을 어떻게 돌려요?

이걸 이해하기 위해 2D 예제를 먼저 봅시다.

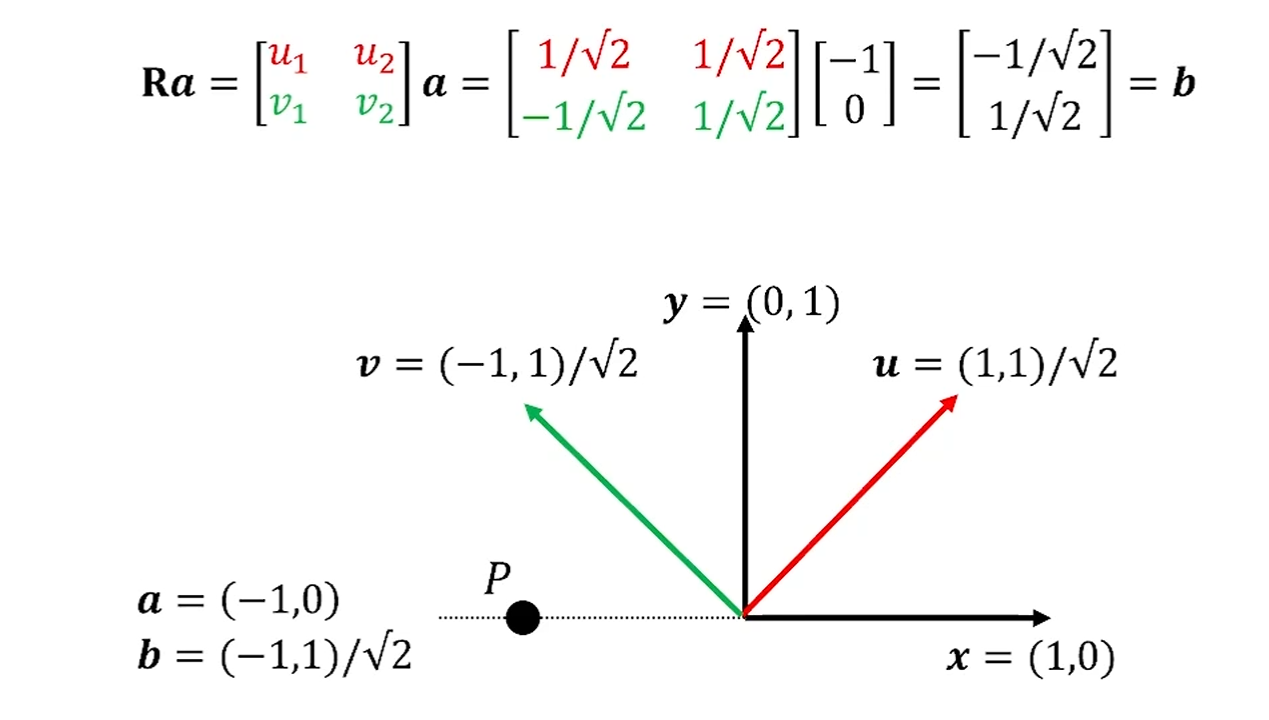
특정한 점 $P$를 x,y에서 생각한 representation과 u,v에서 생각한 representation이 다르죠?

즉 $(-1,0)$을 $(-1,1)/\sqrt2$로 바꿔주고 싶은 겁니다.

1. $u, v$를 $x,y$의 관점에서 씁니다. 그게 $u_1, u_2, v_1, v_2$가 됩니다.
2. 그걸 가로로 쓴 matrix가 변환 matrix입니다.

즉, target이 되는 frame의 basis vector를 가로로 써주면 된다.가 핵심.

조금 더 formal하게 봅시다.

이제 $u, v, n$을 $x,y,z$의 관점에서 작성하면,

basis가 정해졌으니 어떤 vector든 linear combination으로 쓸 수 있겠죠?
그래서
$u = u_1x + u_2y + u_3z$
$v = v_1x + v_2y + v_3z$
$n = n_1x + n_2y + n_3z$ 로 쓸 수 있어요.

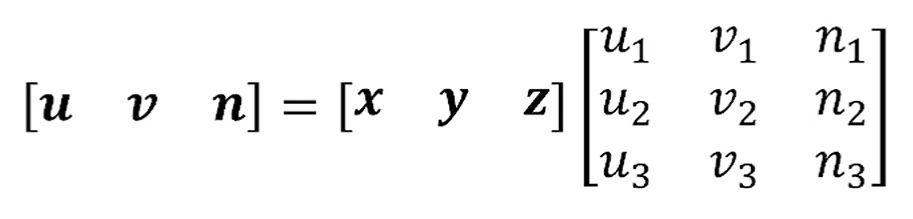
예쁘게 쓰면 이렇게 되구요.

다음으로,
$x,y,z$에 대한 representation이 $a$고,
$u,v,n$에 대한 representation이 $b$라고 할 때,
$a_1x + a_2y+ a_3z = b_1u + b_2v + b_3n$이 성립하겠죠?

그럼 추려서 적으면 다음과 같아지고,

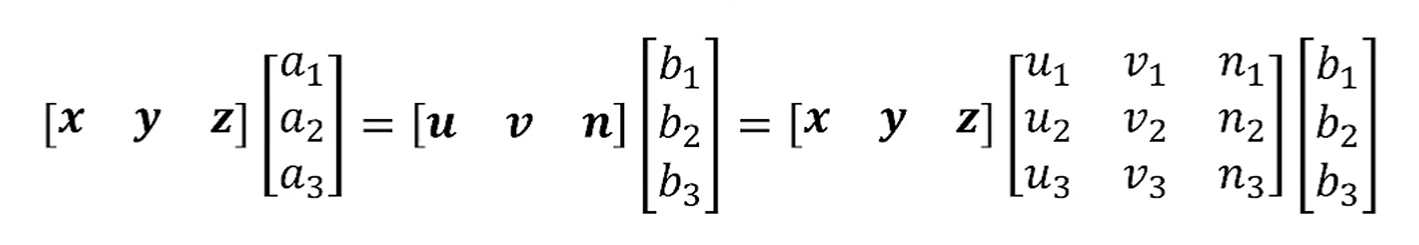
공통항인 $[x,y,z]$가 사라질 수 있죠?
그러면

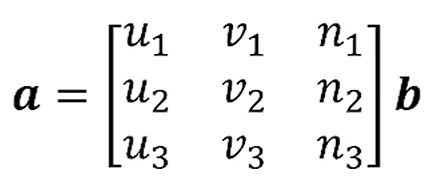
가 남습니다.

그래서 뭘 한거에요?

$x,y,z$축에서의 좌표 $a$를 $u,v,n$축에서의 좌표 $b$로 변환하는 matrix를 구한거에요.

앞서 2D 예시에서는, basis vector를 가로로 쓴 게 핵심이었잖아요.
근데 지금은 basis vector를 세로로 썼네요. 에이, 그러면 통일성이 없죠.

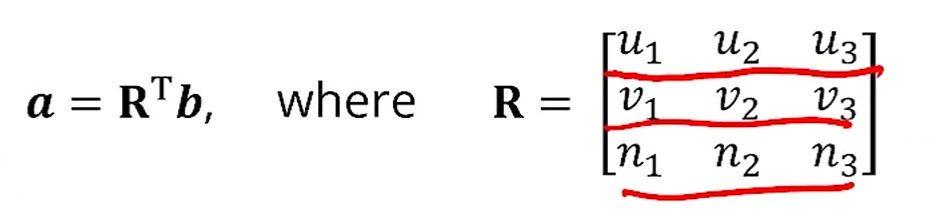
basis vector를 가로로 쓴 걸 R이라고 할 때, $a = R^Tb$가 성립합니다.

근데 우리가 원래 원하는게 뭐였죠??

a를 주면 b를 구하는게 목표잖아요.

근데 우린 반대로 b를 알면 a를 구할 수 있네요.

그래서 $b = (R^T)^{-1}a$를 써주면,
R이 orthonormal basis이기 때문에 inverse가 transpose와 같아지구요, (캬;;)

$Ra = b$만 남습니다.

이야;; 이게 수학이죠

우리가 원래 구하고 싶었던 LookAt Matrix가 뭐다?

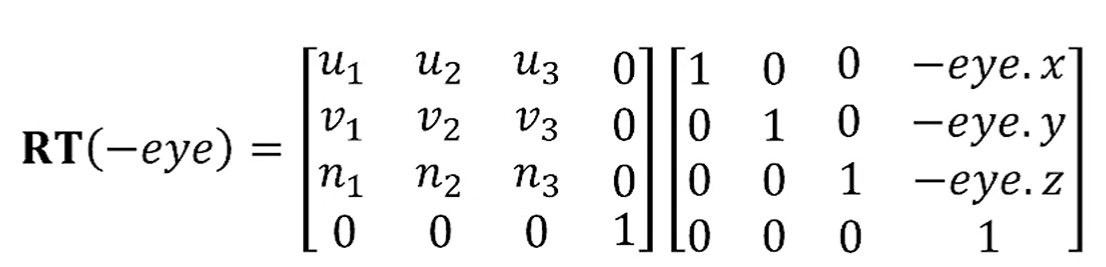
World 원점으로 translate하고, rotation을 해주면 된다.

결론.

Camera를 이동시키는 것과 Model을 반대로 이동시키는 것은 효과가 같다.
(Model-view duality)

따라서 World Space (x,y,z축)을 Camera Space (u,v,n축)으로 바꾸고 싶을 땐,

1. Model을 eye 반대 방향으로 이동 시킨다
2. rotation을 한다.