ML에서는, 어떤 모델에 입력변수를 주면, 알아서 gradient descent를 시행한 후,
gradient를 계산해줍니다.
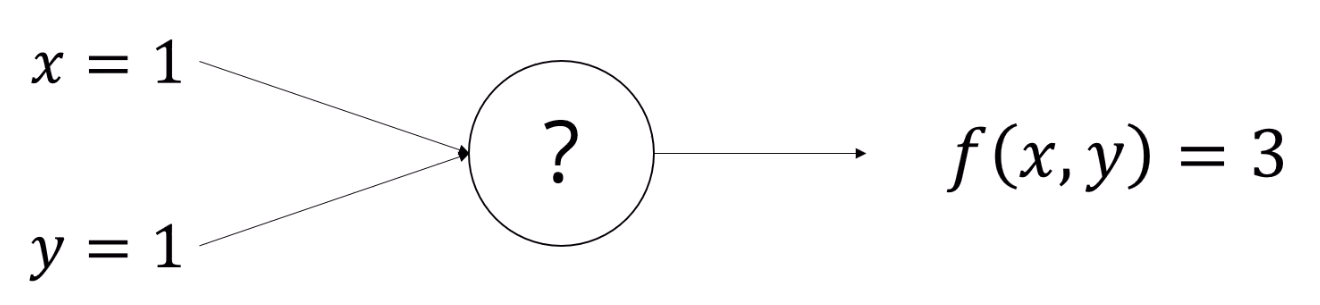
이런 x,y를 함수에 넣으면 '3'이라는 값이 나오는 함수 f가 있다고 합시다.
우리는 ?가 뭔지 모릅니다.
x, y가 어떻게 바꿀 때 f(x,y)가 최소가 되는지 알아보려면,
x랑 y를 일단 몇번 바꿔서 대입해 보는 방법이 있겠습니다.
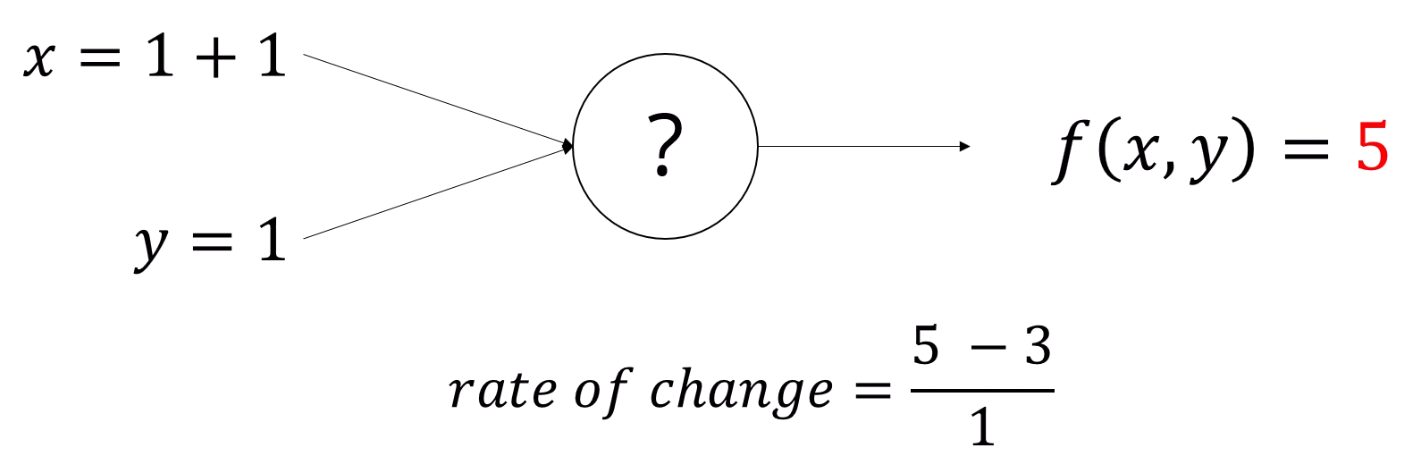
x에 2를 넣었더니 3 -> 5로 바뀌었네요.
그럼 우리는 'x가 늘어나면 f(x,y)도 늘어나는 관계가 있지 않을까?' 라는 가정을 할 수 있습니다.
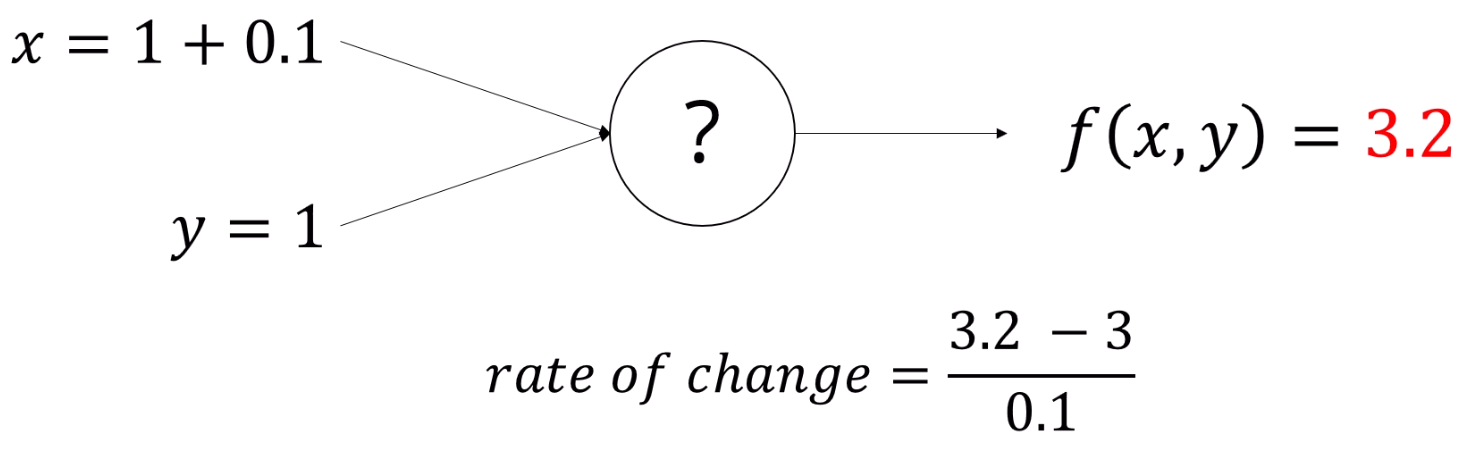
1보다 더 작은 값을 넣어봤더니, 점점 x = 1에서의 변량과 비슷해지는 것을 느낄 수 있습니다.
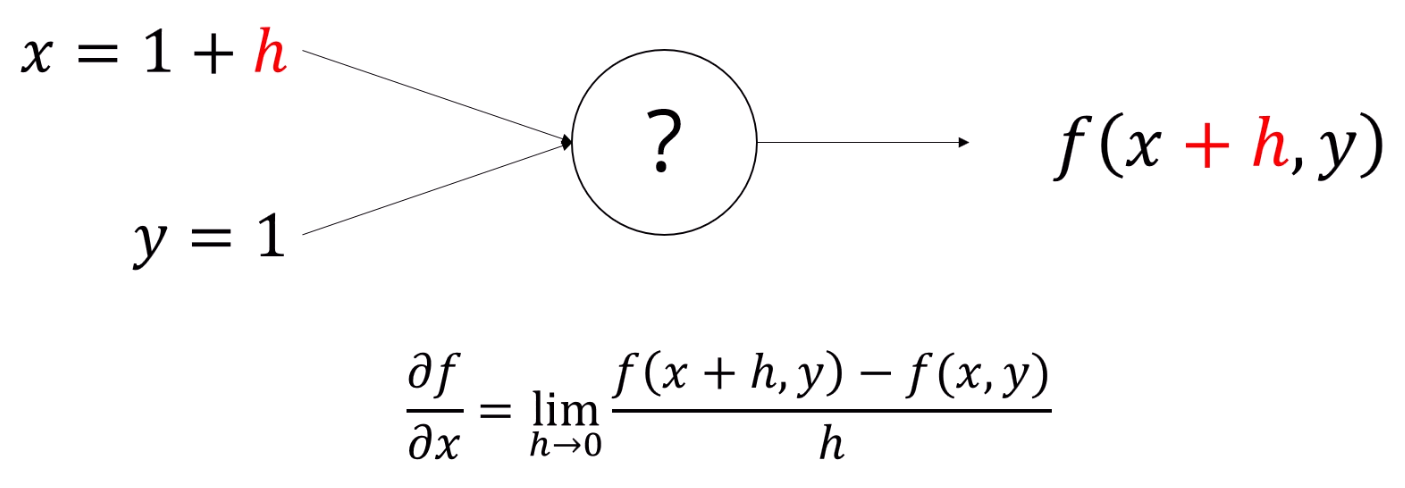
극한으로 작은 값인 h를 넣으면, 그 순간변화량은 다음과 같이 표현되고,
f에 대한 x의 gradient라고 표현을 할 수 있습니다.
미분계수의 기본적인 정의입니다.
즉, f가 뭐든지 간에, 각 차원에서의 x의 순간 변화량을 근사할 수 있습니다.
주어진 x,y에 대해서 x,y를 아주 조금만 바꾼 다음 바꾼 양으로 나눠주면 되네요.
이걸 이제 수치적 미분이라고 칭합니다. (Numerical Derivation)
이 알고리즘은, f를 알던 모르던 미분이 가능하건 말건 쓸 수 있습니다.
구현도 매우 쉽구요.
단점은, 산술적으로 오차가 발생 할 수 있습니다. (Floating-point precision)
또, 숫자는 얻을 수 있지만, 수식은 얻을 수가 없습니다.
어떻게 x, y가 조합되어 이런 기울기가 나왔는지 알 수 없지요.
그리고, 함수가 커지면 계산이 costly해집니다.
그래서, 수치적 미분이 아닌 분석적 미분을 하게 됩니다.
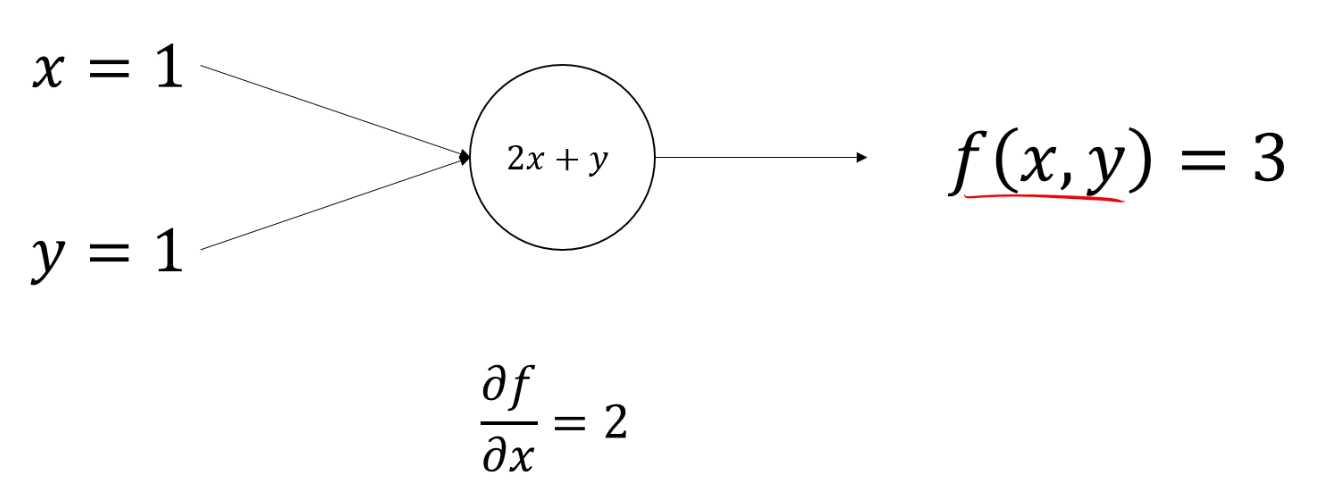
f(x,y)의 식을 알고 있다면, x의 gradient를 알 수 있습니다.
중요한 점은 f의 식을 알아야 한다는 점이겠죠.
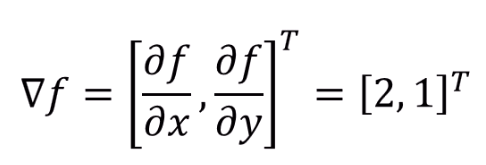
아무튼, gradient를 이용하면,
f가 어느 방향으로 향할 때 가장 최대로 커지는지 를 알수 있습니다.
반대로 말하면,
gradient의 반대 방향으로 가면 최소로 향할 수 있겠지요.
그게 gradient descent의 기본 원리입니다.
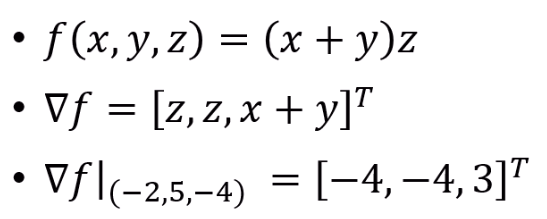
이런 쉬운 함수가 있다면, gradient도 쉽게 구할 수 있고,
특정한 점에서 어떤 방향으로 가면 제일 f가 커지는지,
반대로 말하면
어느 방향으로 가면 극소를 향할 지 쉽게 구할 수 있습니다.
그러면, 함수가 복잡해지면 어떻게 될까요?
Gradient of Complex Functions
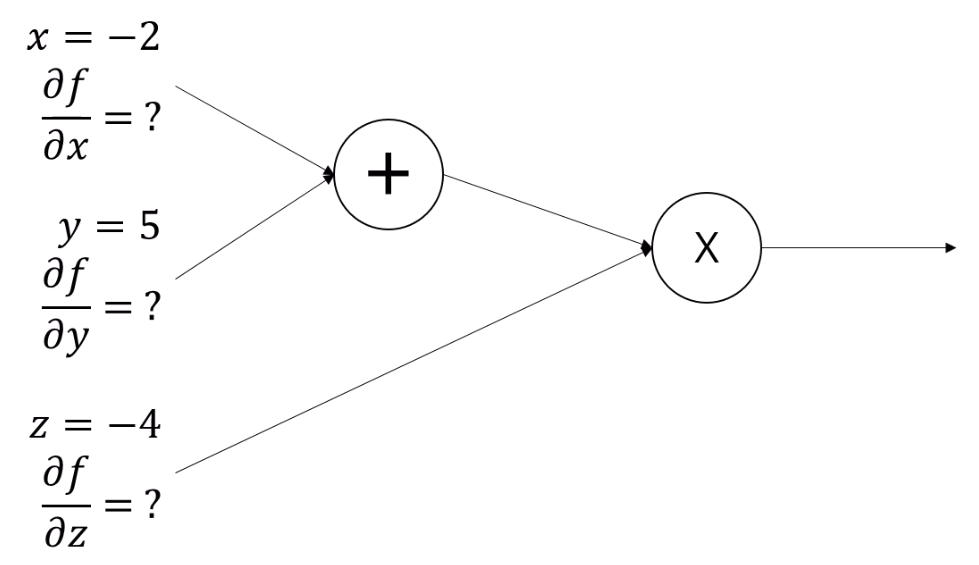
먼저 circuit diagram을 그려줍니다.
핵심은, f가 뭔지 알고는 있어야 한다입니다.
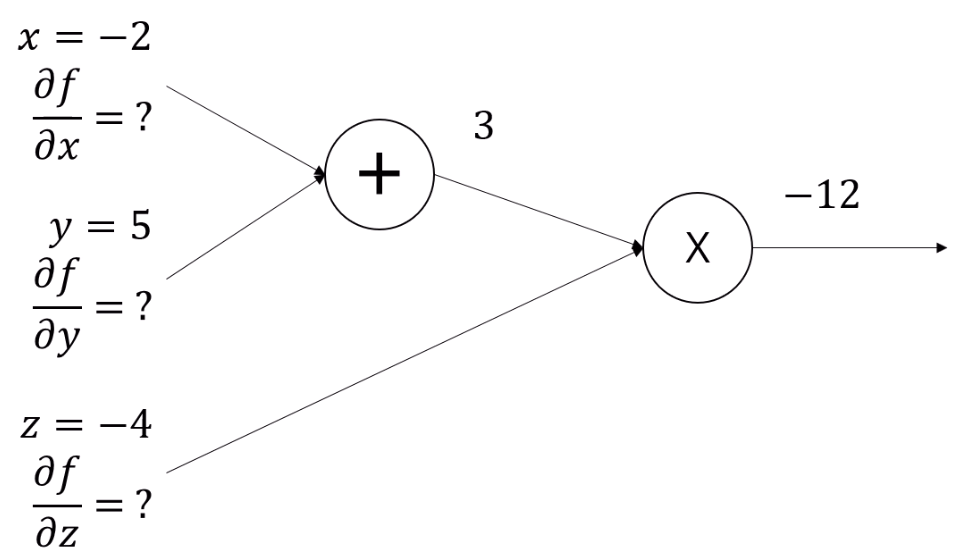
그 Tree의 실제 계산 결과를 쭉 적어줍니다.
(-2 + 5)는 3이고, 3 * (-4)는 12죠.
이 과정을 Forward Pass라고 합니다.
Forward Pass가 끝나면 모든 node의 출력값을 다 알게 되죠.
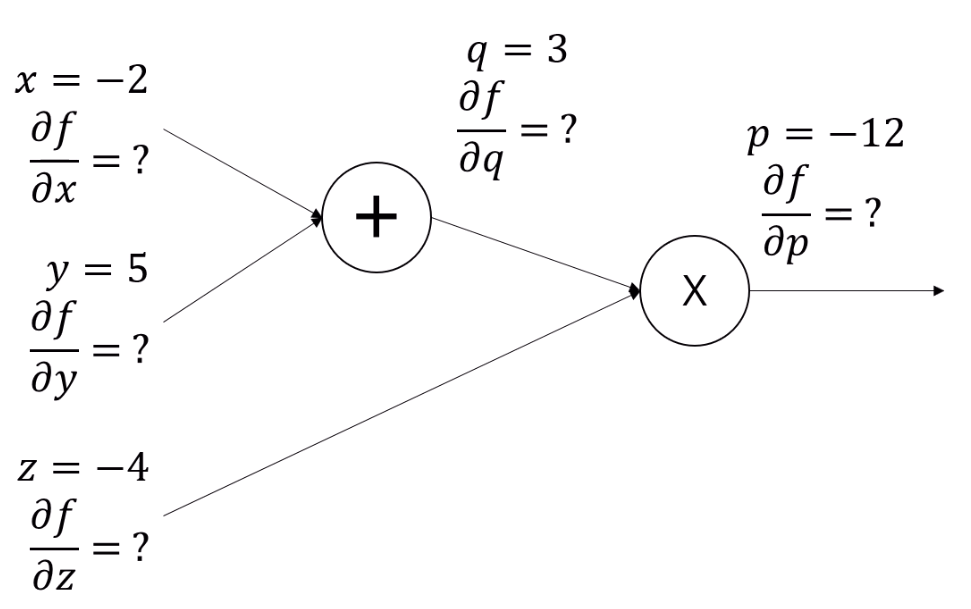
다음, internal node들에게 다 이름을 지어줍니다.
leaf node를 포함해서 모든 node를 동일하게 취급할 수 있겠네요.
이러면
x + y = q,
q * z = p의 식이 추가가 됩니다.
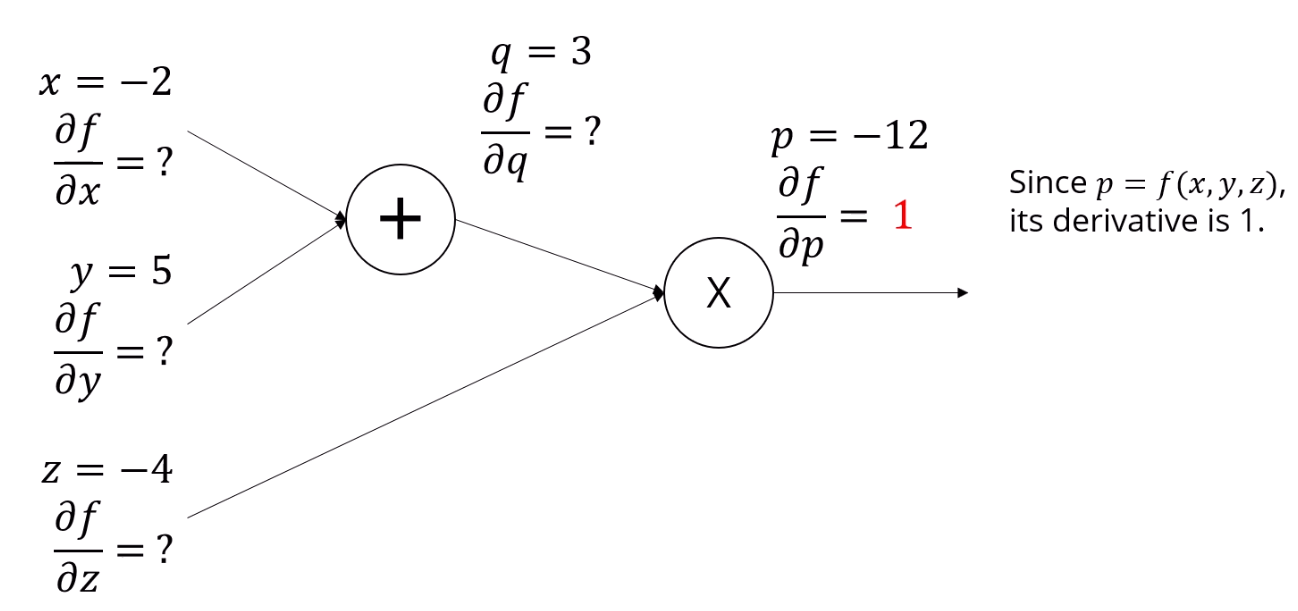
이제 Backward pass를 해줍니다.
입니다.
p는 출력값이잖아요?
출력값을 출력값으로 미분하면 당연히 1이 나옵니다.
자기 자신을 자기 자신으로 미분하니까요.
다음 식을 이용하면, partial f over partial q도 구할 수 있습니다.
p = qz를 이용합니다.
앞서 얻은 z는 -4죠. 즉
이런 방식으로 계속 구해주는 겁니다.
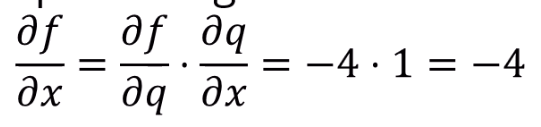
( q = x+y이며, fq gradient는 이전단계에서 구했음을 이용 )
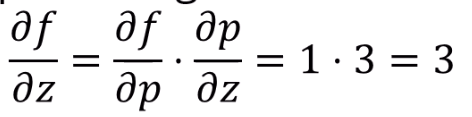
( p = qz이며, fp gradient는 이전단계에서 구했음을 이용 )
이런 방식을 적용하면 얼마나 함수가 복잡하건 gradient를 구할 수 있습니다.
각 Node에서, Upstream Gradient, relationship between node and its parent, (이건 식을 아니까 이미 알겠죠) value of node and its siblings (Forward pass에서 구해집니다)
를 알면 됩니다.
이런 방식을 Backpropagation이라고 부릅니다.
Forward pass해서 어떤 값을 쭉 진행시켜 구하고,
정답 값과의 오차를 구한 후,
그 오차를 upstream gradient로 두고 그걸 밑으로 역전파를 시켜서,
입력값들이 그 오차에 얼마나 기여하는지 계산합니다.
이걸 Error Backpropagation이라고 칭합니다.
Operators Behavior
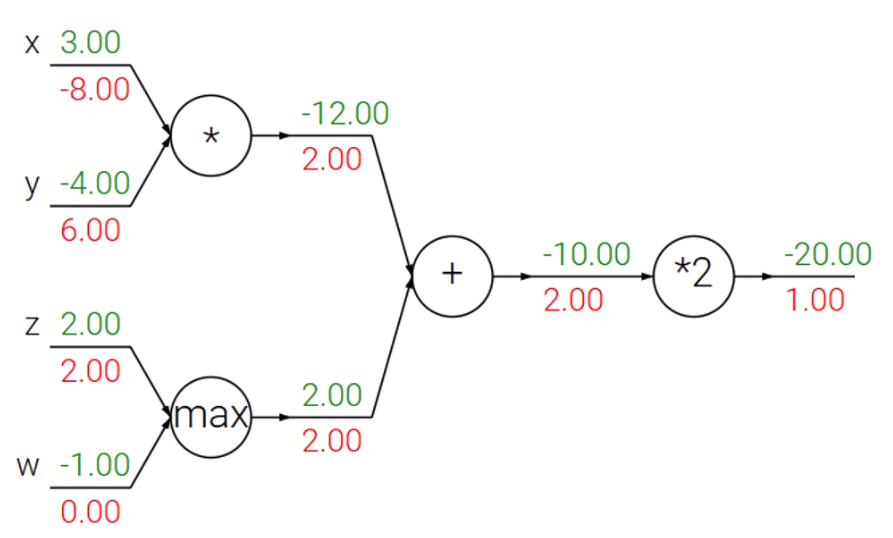
이 식을 표현하면
가 됩니다.
이걸 직접 전개해서 미분하고 어쩌고 하면 어렵고 힘들죠.
빨간 값을 gradient이고, 초록 값이 forward pass된 출력치입니다.
이를 바탕으로 계산기를 두드릴 수 있습니다.
여기서 알 수 있는 정보들이 조금 있습니다.
- 상수곱셈은 그대로 gradient를 역전파한다.
라고 합시다.
의 관계가 성립하니, 자연스럽게 선행 node의 gradient가 곱해진만큼 역전파되네요.
- 더하기 연산자는 gradient를 나눈다.
자명하죠?
- 곱하기 연산자는 서로가 서로의 gradient가 된다.
일 때,
이며, upstream gradient는 어떻게 구해져 있을 테니,
그 upstream gradient에 x 입장에선 y가, y 입장에선 x가 곱해지겠네요.
- max 연산자는 영향을 준 값만 반영되며, 그렇지 않으면 0.
gradient 역전파의 근본적 목표가 해당 인자가 최종 gradient에 얼마나 영향을 미쳤는지 확인하는 것이라고 했습니다.
max(z,w)의 경우, z가 더 크다면 w는 태초에 하등 영향을 미치지 못했습니다.
따라서 upstream gradient를 z만 받고 w는 못 받겠죠.
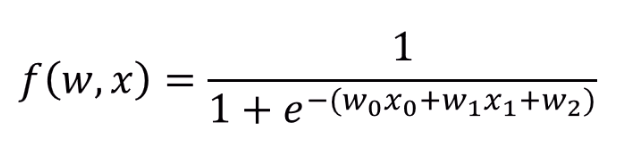
이런 작살나게 어려운 식도, 에 대해 circuit diagram만 잘 그리면 쉽게 분석이 가능합니다.
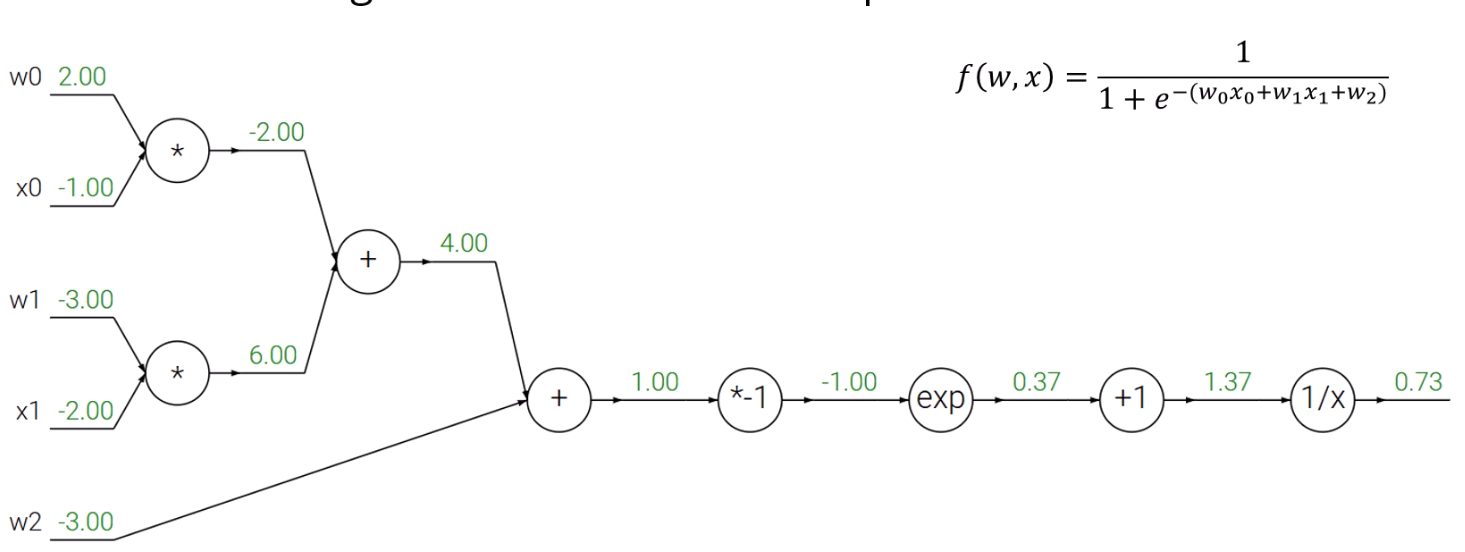
먼저 Circuit diagram을 그리고, forward pass를 해줘야겠죠.
아까는 보지 못한 exp, 역수 등 여러 연산자가 보입니다.
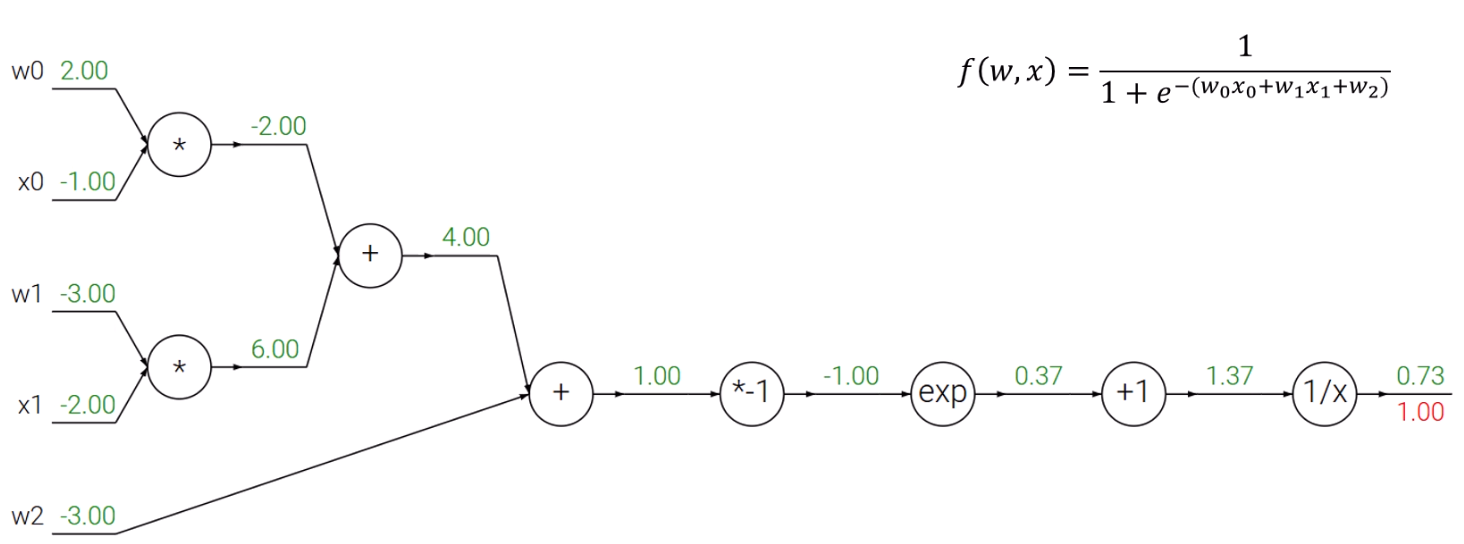
마지막 node의 gradient는 볼것도 없이 1이죠.
(+1) node가 p고, (1/x) node가 q라고 할 때,
가 성립을 하고, 가 성립을 합니다.
의 출력값이 1.37이니, 이 되네요.
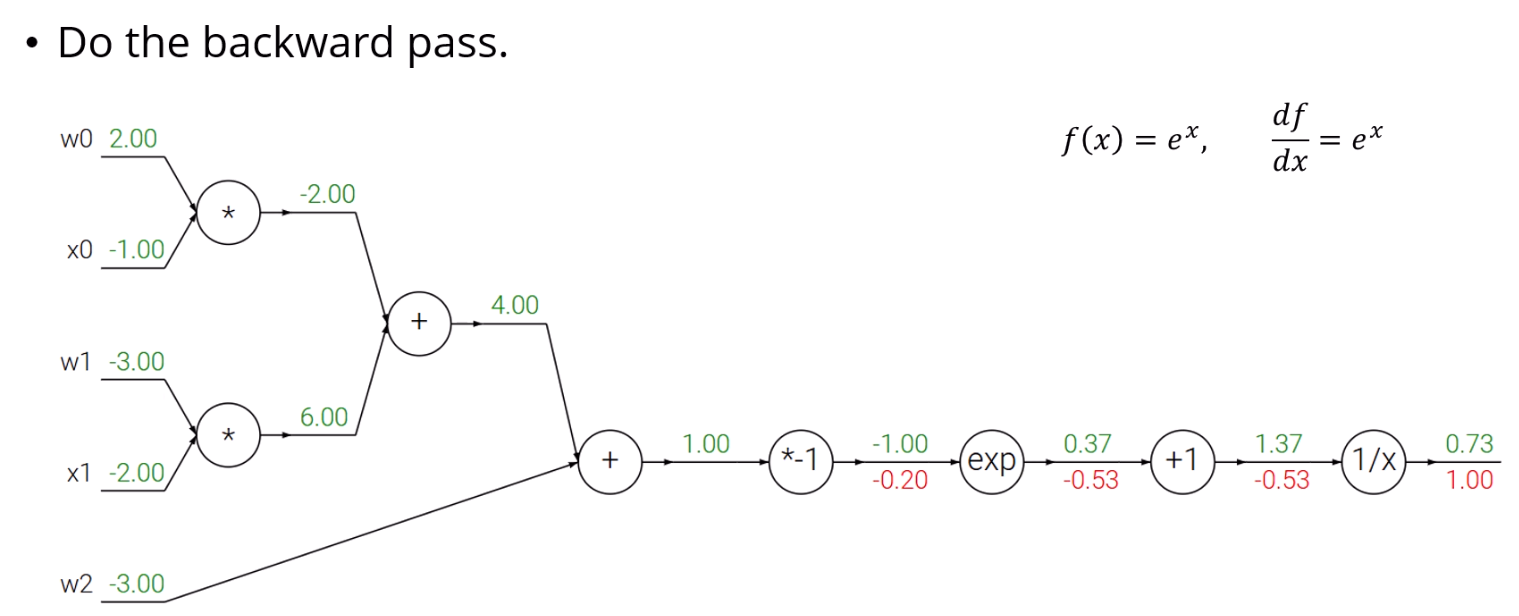
(*1) node를 p, (exp) node를 q라고 할 때,
가 성립하고, 가 성립을 합니다.
의 출력값이 -1.00이니, = 0.36이고,
이 되네요.
그 후로는 그냥 평범하게 해주면 됩니다.
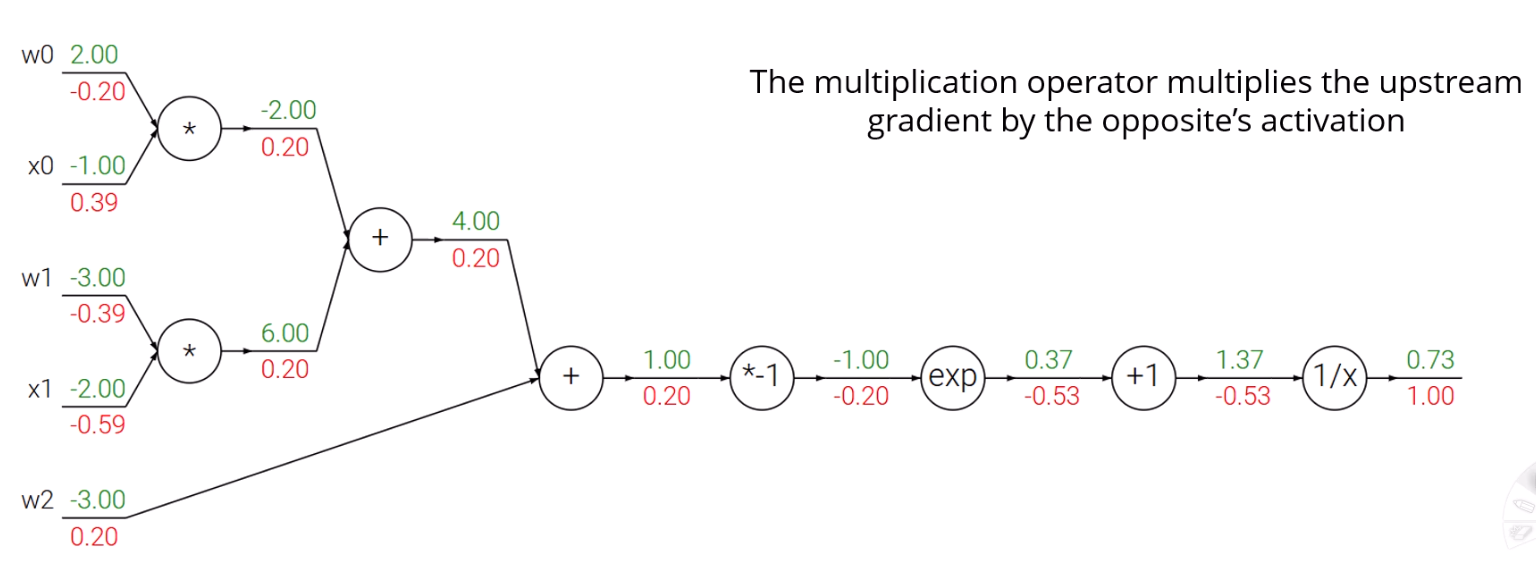
Additional Exploration
출력값 0.73을 1로 올리고 싶다면, 어느 input을 올려야 할까요?
은 gradient에 미치는 영향이 음수입니다.
얘네를 증가시키면 정답값은 낮아질겁니다.
를 높여야겠네요.
실제 세상이라면, 이 매개변수들 중 어느 변수들이 실제로 update될 수 있는 값인가요?
보통 logistic regression에서는 입력에 weight를 곱해서 값을 내놓습니다.
은 입력 데이터에요.
현실적으로는 매개변수인 만 건드릴 수 있습니다.
마지막으로, 곱하기 연산자에서 양쪽이 다 0이면 어떻게 되나요?
같은 관계가 성립하면 입장에선 y의 값을 gradient로, vice versa로 받습니다.
둘 다 0이라면, gradient가 사라져버리겠네요.
이런 걸 Gradient Vanishing이라고 부릅니다.
그래서, gradient가 둘 다 0인 경우에는 noise를 조금 줘서 강제로
0이 아닌 값으로 나오게 한다는 등의 처리를 합니다.
