Decision Tree가 뭔가요?
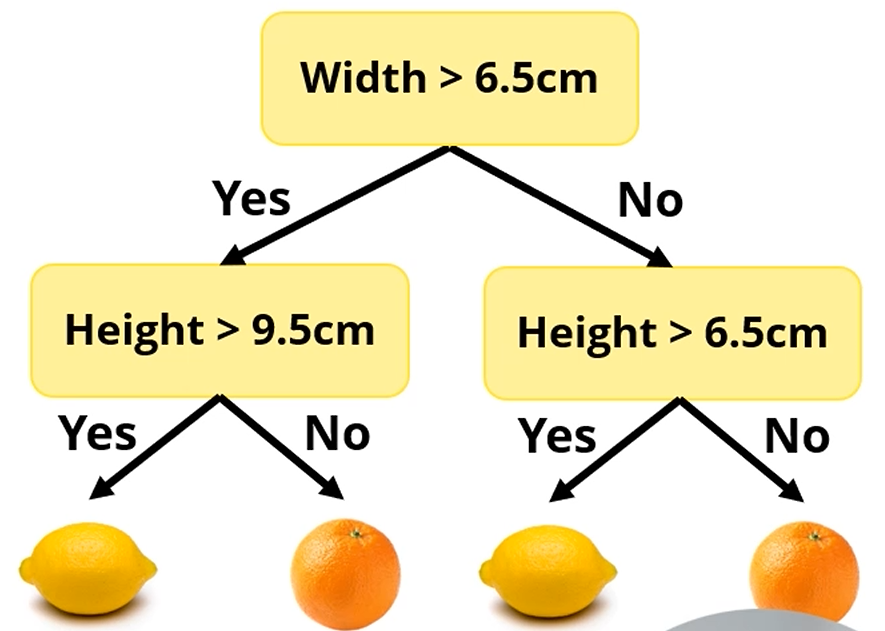
Decision Tree는 특정 Attribute에 따라 data를 branch로 분류하는 tree를 decision tree라고 칭합니다.
이런 경우에는 [너비, 높이]의 attribute를 보유한 데이터를 tree에 따라
레몬인지, 오렌지인지 분류하는 문제가 되겠네요.
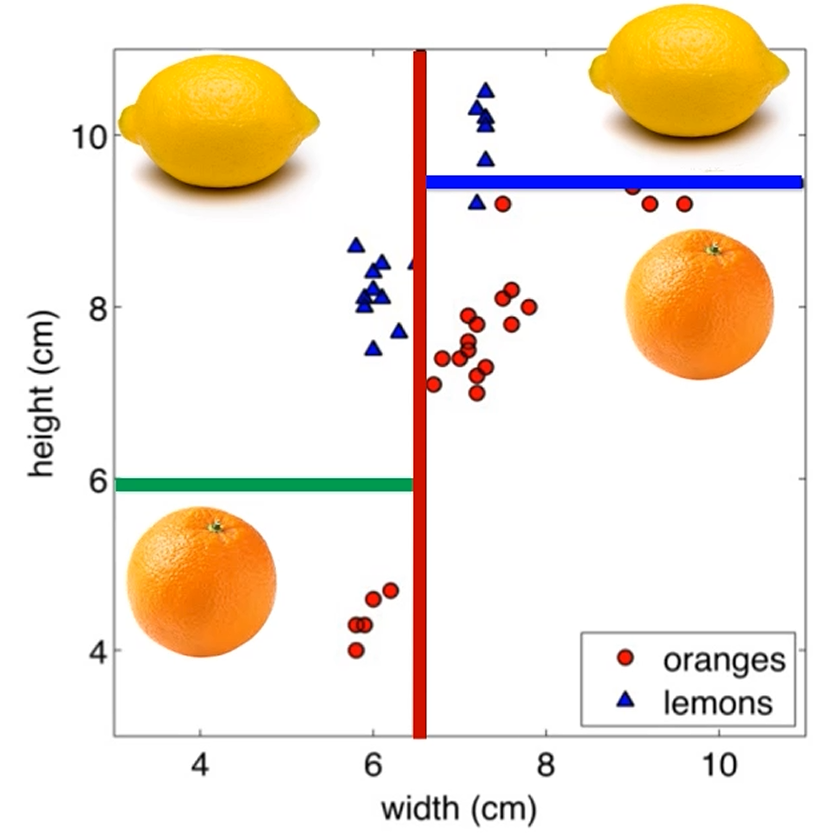
Decision Tree로 전체 데이터에 결정 경계 (Decision Boundary)를 그을 수 있습니다.
경계로 구분된 구역의 특정 구역에 속하면 A, 특정 구역에 속하면 B처럼 구분이 되는거죠.
결국 분류가 목적인 Tree라고 보면 됩니다.
Decision Tree에서 존재하는 Path들은,
Attribute 영역에서의 <공간>으로 해석할 수 있습니다.
위의 좌표평면에서는, 제일 왼쪽 아래 공간은 주어진 Decision Tree에서 제일 오른쪽 Path겠죠.
제일 오른쪽 Path로 분류되는 친구들은 전부 제일 왼쪽 아래 공간에 포함됩니다.
How to build a Decision Tree?
수많은 정답 Label을 담고 있는 Data들이 존재하고,
우린 그 Data들을 이용해 Decision Tree를 만들고 싶습니다.
우선, Root Node에서 잘 쪼개는 게 중요합니다.
수많은 가능성을 고려해야 하는데, Optimal한 Decision Tree (Smallest Decision Tree)를 만드는 문제는 NP-Complete합니다.
그래서, Greedy Heuristic을 이용합니다.
각 Stage에서, 미래는 신경 쓰지 말고 최선의 Attribute를 택하여 쪼갭니다.
그럼, 각 stage에서 어떤 Attribute로 쪼개는 것이 최선일까요?
최선이 무엇을 말하는 걸까요?
그리고, 언제까지 쪼개야 할까요?
Building a decision tree - Choosing a good split
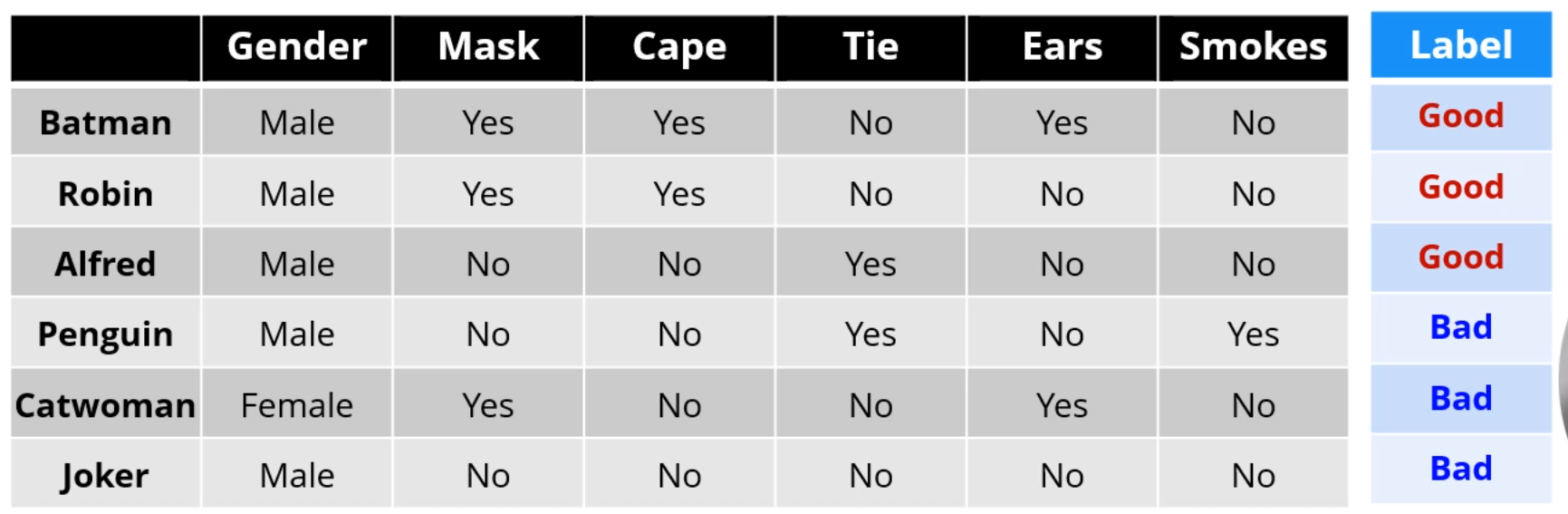
다음과 같은 영웅 Data Set을 이용해 Decision Tree를 구성합니다.

둘 중 뭐가 더 좋은 쪼갬일까요? 여기서는 Cape입니다.
Cape로 쪼개는 것이 Uncertainty가 적습니다. 훨씬 더 확실성을 갖고 분류를 할 수 있죠.
학습 데이터에 대해 더 잘 예측을 하는 Split이죠.
그렇게 쪼개서 만들어진 그룹들끼리 동질적일 수록 좋은 Split입니다.
여기서 Entropy가 등장합니다.
Leaf Node에 있는 sample들이 Same Class라면,
Uncertainty가 적으며, 좋은 Prediction이라고 할 수 있죠.
또한, Entropy가 적습니다.
Information Entropy는 다음과 같이 정의되죠.
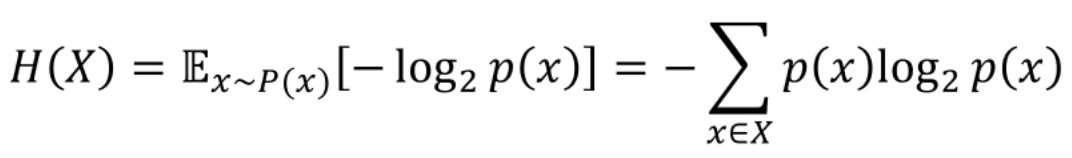
데이터셋의 값들이 갖는 평균적인 정보량입니다.
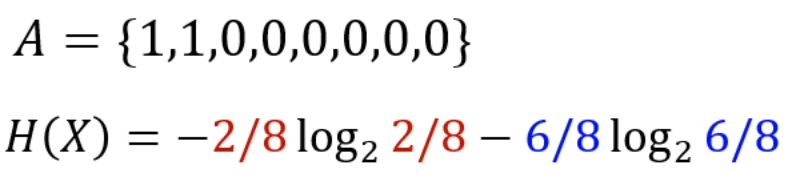
해당 데이터셋은 8개 중 2개가 하나의 class로, 6개가 하나의 class로 분류됩니다.
엔트로피를 이렇게 정의할 수 있게 되죠.
이 Entropy를 이용해 Split이 좋은 Split인지 아닌지를 결정합니다.

어느 Entropy가 더 좋을까요?
대충 봐도 일단 B가 더 좋은 분류입니다.

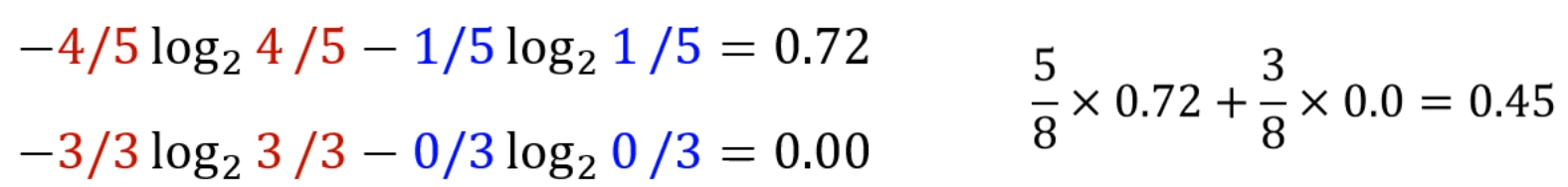
실제로 공식을 적용해도 B가 조금 더 우월한 분류네요.
포인트는 양 Branch의 엔트로피 평균을 낼 때,
분류된 원소의 절대 개수에 따른 비율을 곱해주는 것입니다.
공식을 잘 보면 알 수 있죠!
0.97과 0.92의 평균을 내는게 아니라 5:3의 비율을 고려해서 평균을 냈네요.
(사실 당연한 내용이기도 하구요.)
우리는 Information Gain을 다음과 같이 정의합니다.
자르기 전 Entropy가 0.9고, 자르고 나서 Entropy가 0.4라면,
Information Gain은 0.5만큼이 됩니다.
그리고 우린 Information Gain이 더 큰 쪽으로 자르게 됩니다.
그리고 Information Gain이 특정 threshold보다 작다면, 잘라도 큰 이득이 없다고 판단하고,
자르는걸 멈추는 Pruning 작업에 들어갑니다.

그러면 이제 이 데이터셋에서 Cape, Tie 중 어느게 더 이상적인 Split인지 알 수 있습니다.
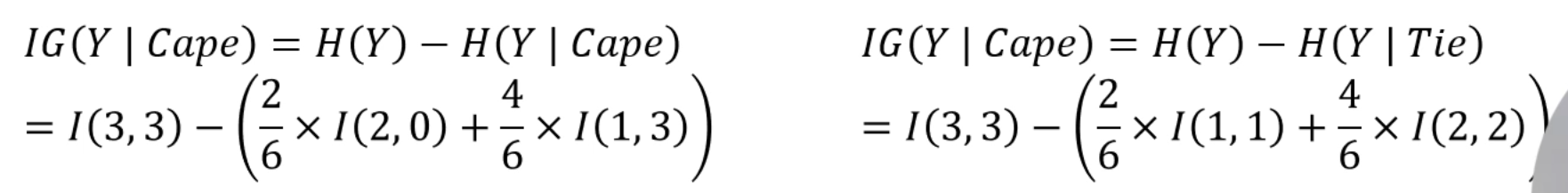
기존의 데이터셋의 엔트로피에서 새로 분류된 친구들의 Entropy를 빼주면,
Information Gain을 얻을 수 있게 됩니다.
그 IG가 큰 쪽이 더 좋은 분류가 되죠.
ID3
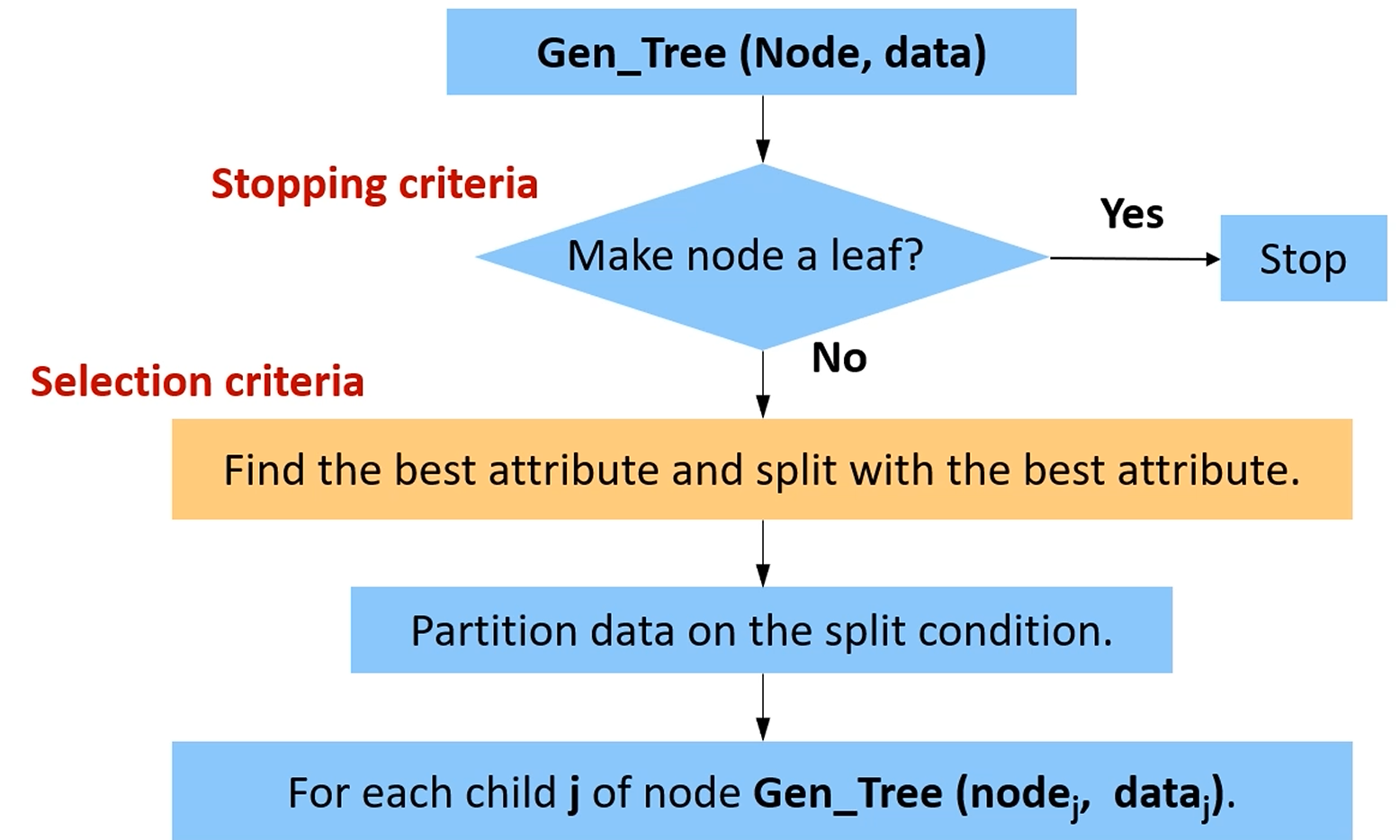
1. GenTree라는 트리를 만듭니다.
2. Node를 더이상 쪼개지 않기로 했다면 멈춥니다.
만약 쪼개기로 했다면,
IG를 이용해 best attribute를 찾고, 데이터를 attribute를 이용해 쪼갠 후,
각 쪼개진 자식들에 대해 GenTree라는 트리를 만듭니다.
결국 배운 내용이네요.
그럼 언제 쪼개기를 멈추나요?
하나의 node에 속하는 모든 sample이 같은 class라면 멈춥니다.
이미 분류가 끝났는데 뭘 더 하겠어요.
아니면, sample이 안 남아도 멈춥니다.
사람, 개, 고양이가 잔뜩 있는 sample을 다리 개수로 쪼갰더니,
다리 0개쪽 branch에는 아무것도 없을 수 있죠.
그리고, 쪼갤 수 있는 attribute를 다 써버려도 멈춥니다.
[강수량], [날씨], [풍량], [풍향] .. 써먹을 수 있는 모든 attribute를 다 썼다면,
더이상 쪼갤 방도가 안 남죠.
[a,a,a,a,b,b,c]라는 sample들이 한 node에 남게 되어도,
이미 가능한 모든 attribute로 다 쪼개봤기 때문에 별수 없습니다.
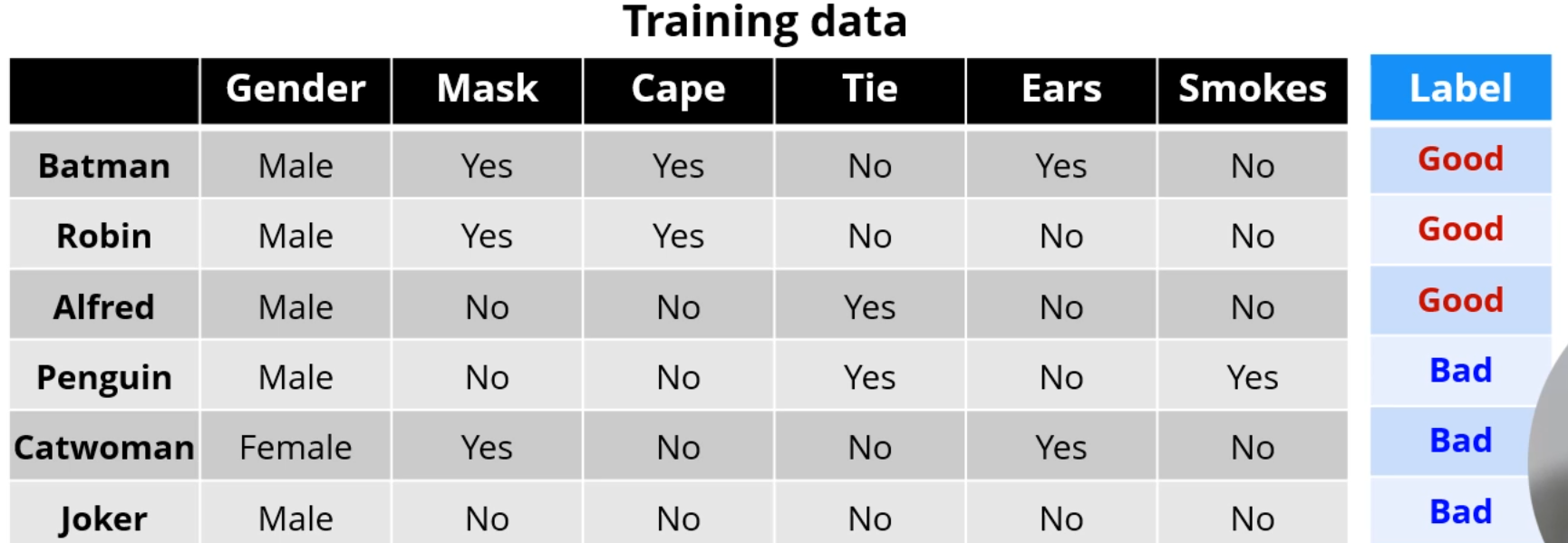
다시 이 데이터셋으로 돌아와서, 분류를 시작해봅시다.
맨 처음 Attribute는 무엇을 써야 할까요?
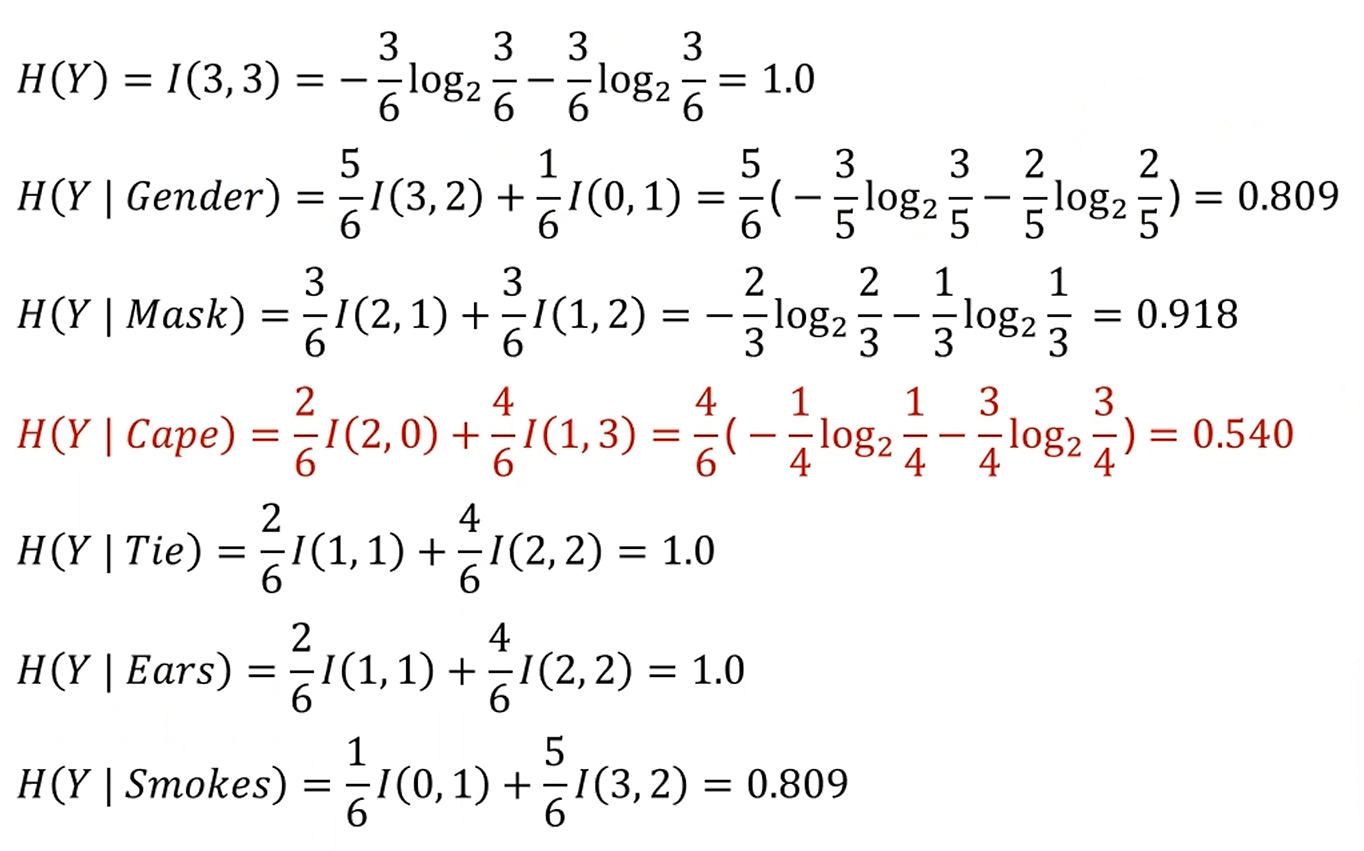
Information Gain을 이용해보면, Cape를 택한 쪽 IG가 제일 높습니다.
맨 처음엔 Cape로 쪼개는게 합리적이네요.
Cape로 쪼개면, Cape[Yes]쪽은 분류가 끝납니다.
Cape[No]쪽을 다시 분류해줘야 합니다.
어떤 attribute로요? 남은 4개의 데이터를 이용해 IG가 제일 높은 친구를 다시 찾아주면 되겠네요.

그렇게 하면 이런 Tree가 완성되고, 여기에 이제 새 Test Data를 이용해 값을 예측하게 됩니다.
Another Example - Binary Classification
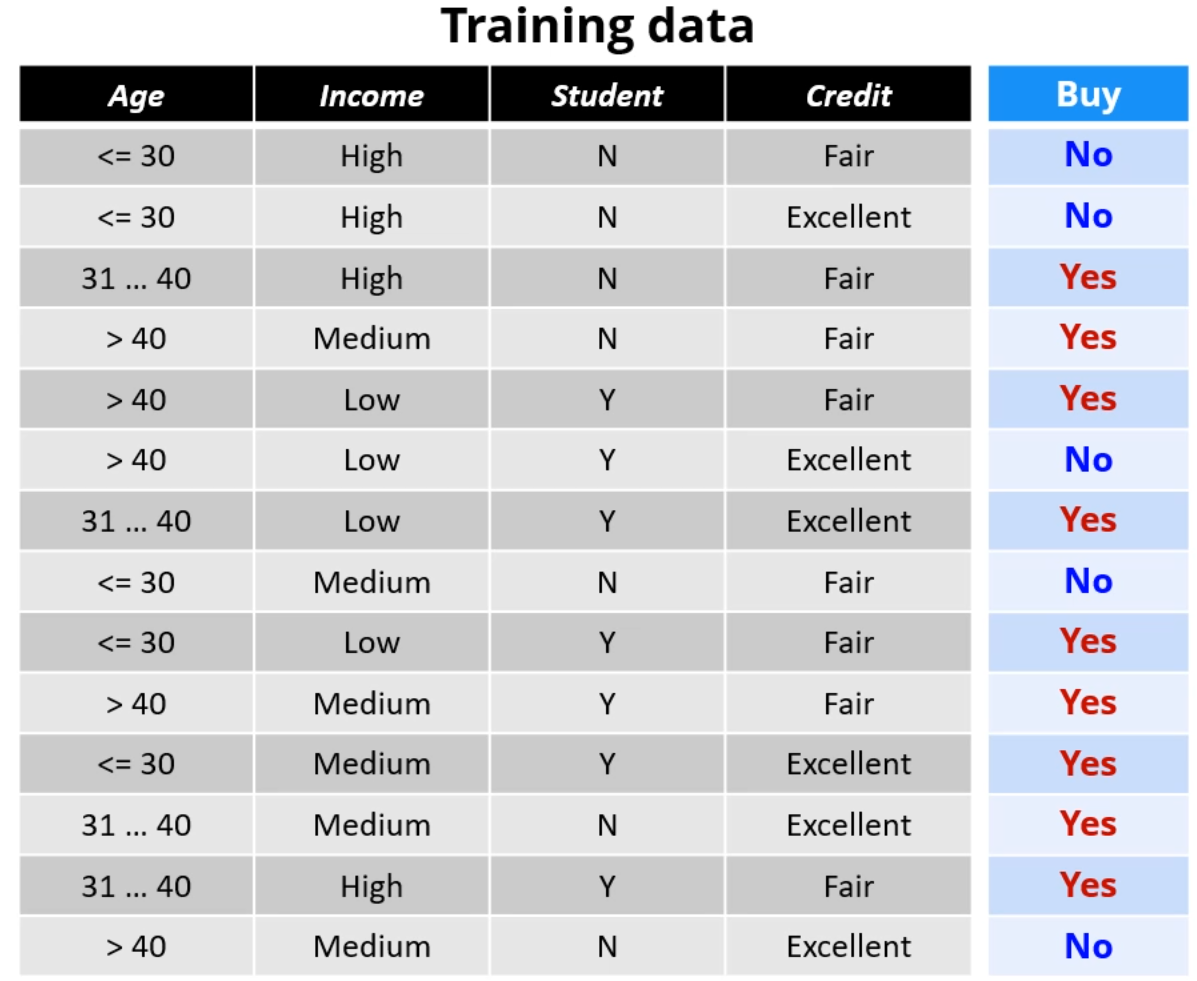
이런 데이터를 놓고 봅시다.
여전히 똑같습니다. 제일 IG가 높은 값을 선택해주면 됩니다.
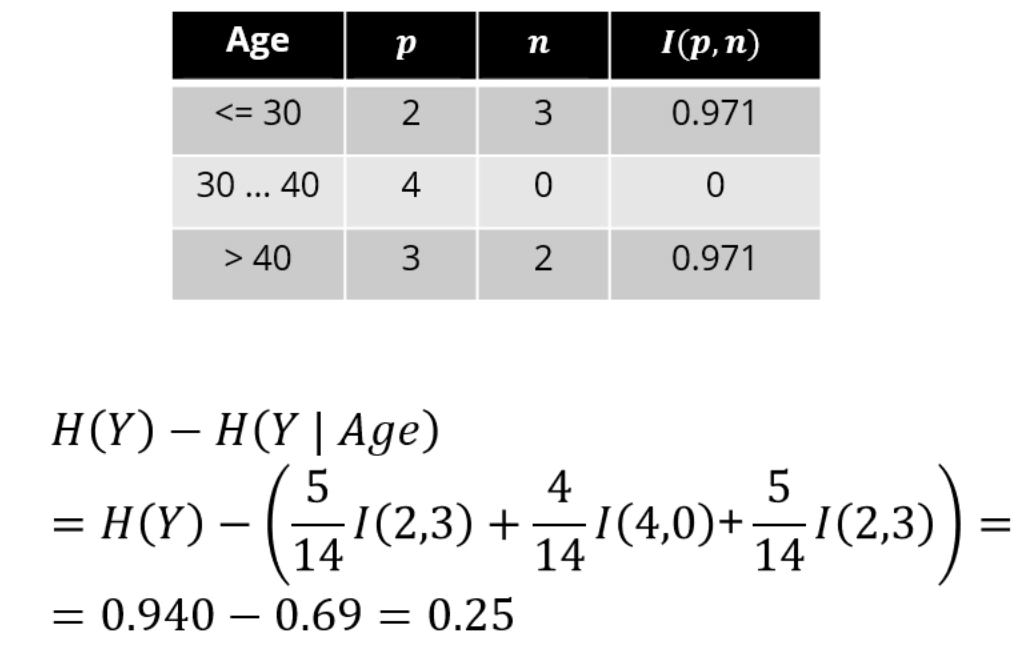
Age를 기준으로 분류하려 한다면, IG는 0.25가 됩니다.
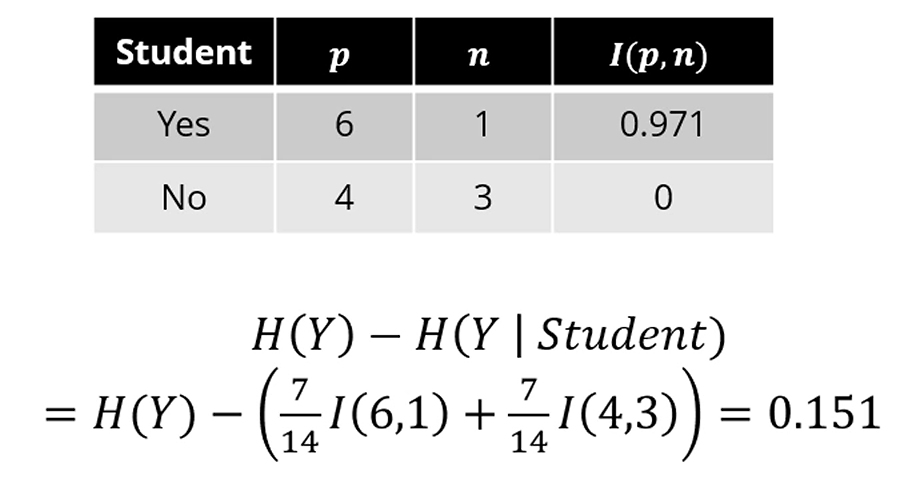
학생여부를 기준으로 두면 IG는 0.151이 나옵니다.
뭐 이모저모 비교해서 Age로 쪼갰다고 합시다.
이제는 Age에 가능한 값이 <=30, 31~40, >40이 있으니 branch가 3개가 됩니다.
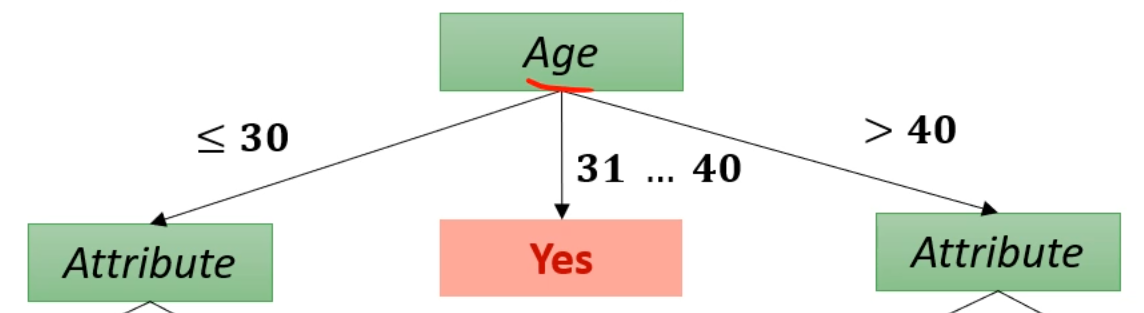
그 중에서도 31~40 branch는 분류가 끝나서 Stopping Condition에 들어갑니다.
이제 각 Branch (<=30, >40)에 대해 각자가 가장 좋은 IG를 갖게 되는 Attribute를 따지면 됩니다.
두 Attribute는 달라도 됩니다. 각자가 독립적인 ID3 Tree라고 가정하면 됩니다.
C4.5
C4.5는 ID3의 개선형 알고리즘입니다.
attribute가 Discrete하지 않고, Continuous해도 작동합니다.
또, IG의 계산법이 더 정교해집니다.
결측값의 적용이 가능해지고,
Tree의 Pruning도 등장합니다.
Continuous Attributes
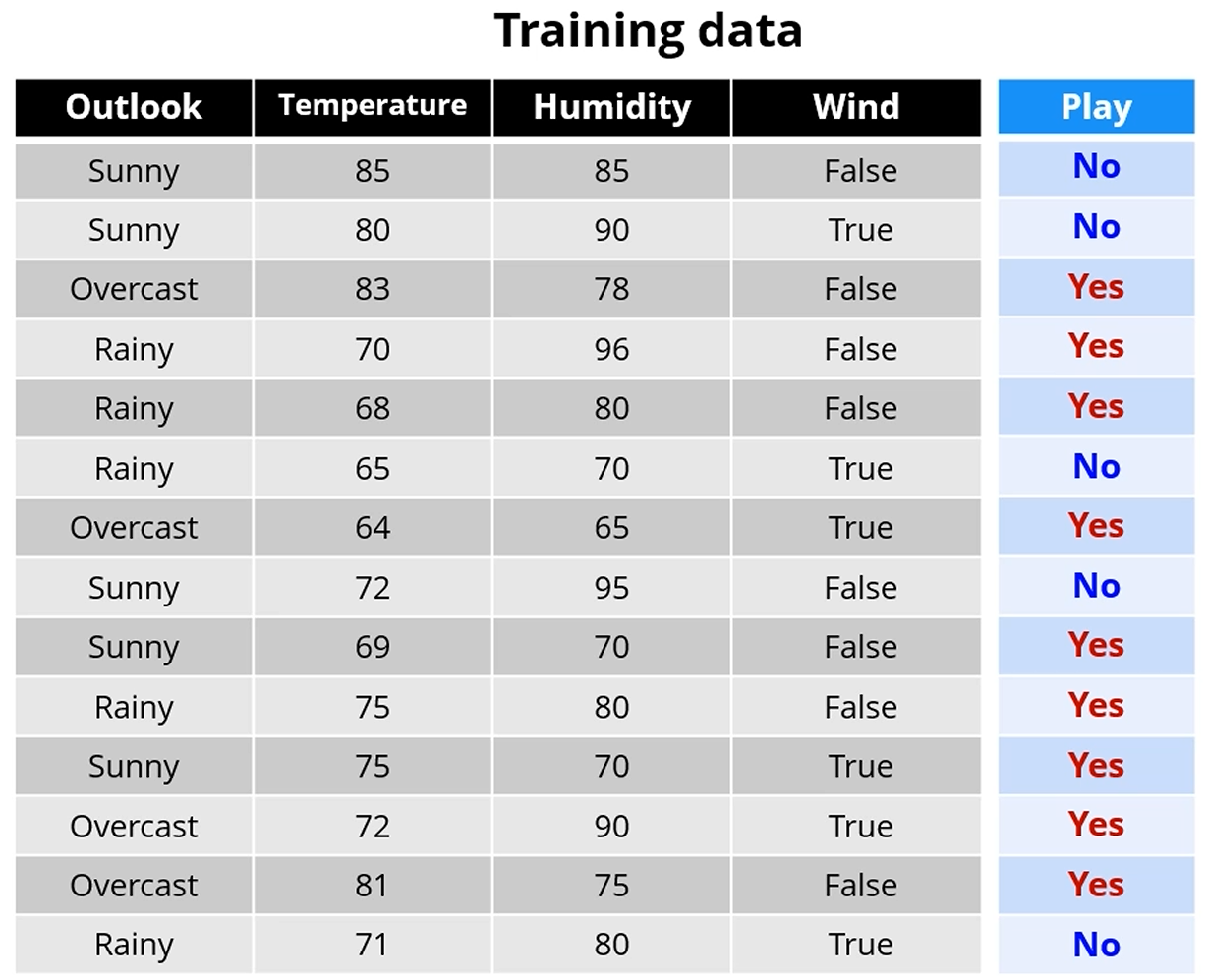
여전히 이진분류 문제이긴 한데,
Temperature, Humidity같은 데이터는 되게 연속적입니다.
이런 경우는 어떻게 할까요?
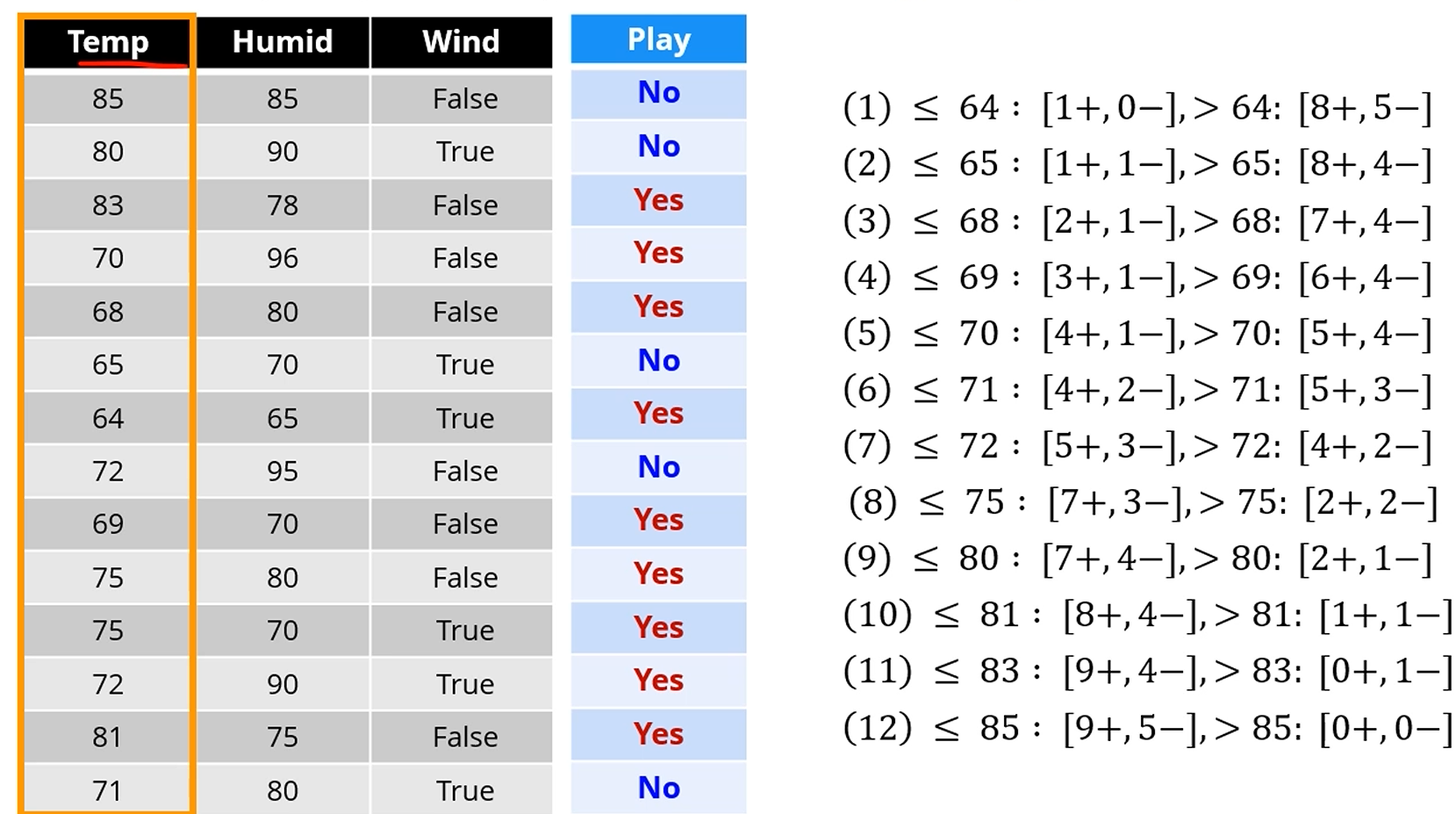
단순한 방법을 사용합니다.
모든 경우에 있어 경우의 수를 전부 생성합니다.
Temperature로 나누고자 한다면, 64, 65, 68, 69, ..를 전부 구분하여 엔트로피를 생성합니다.
(2)번 기준에서는 한쪽 Branch는 2/14 * I(1,1)일 것이고, 다른 한 쪽은 12/14 * I(8,4)가 됩니다.

모든 값에 대해 엔트로피를 다 생성합니다. 그러면 최소값이 나옵니다.
(= IG가 제일 큰 값이 나옵니다.)
그러면 Temperature <= 83? 을 Attribute로 삼아서 분리를 합니다.
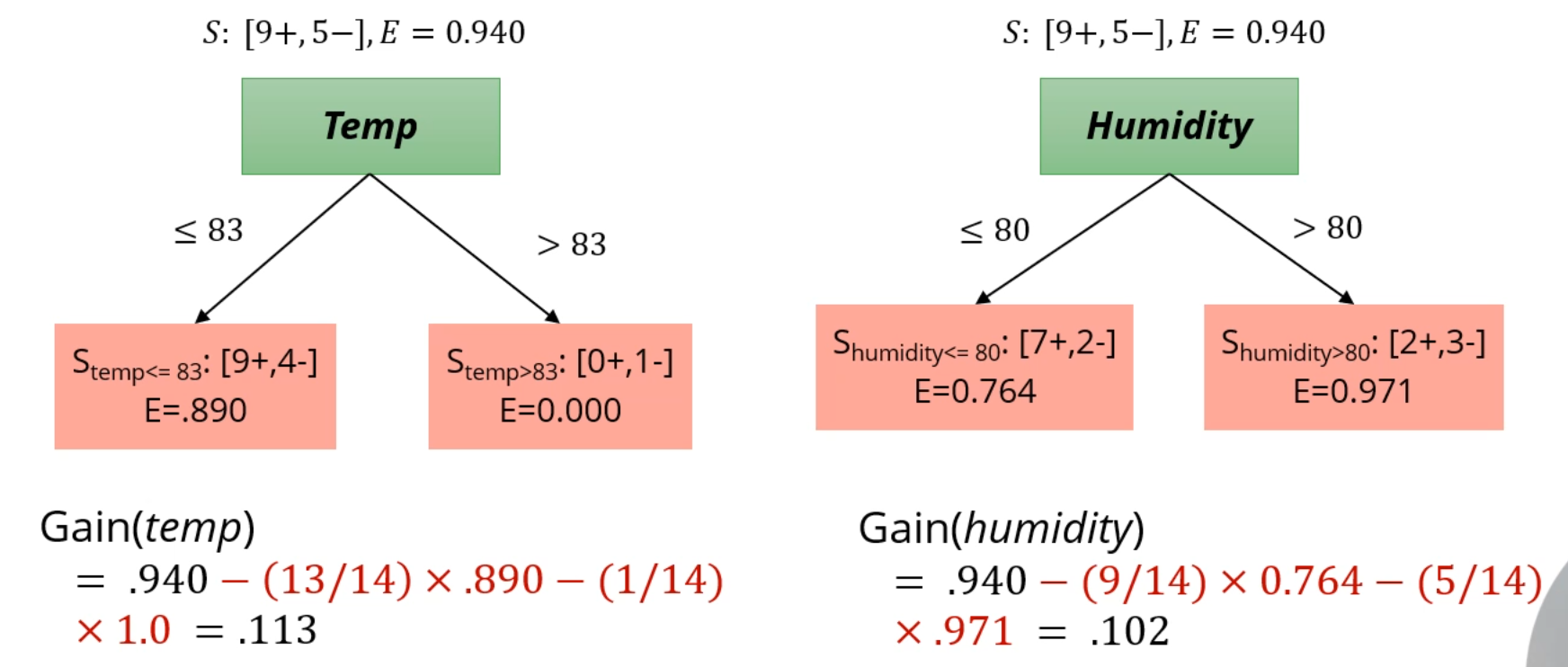
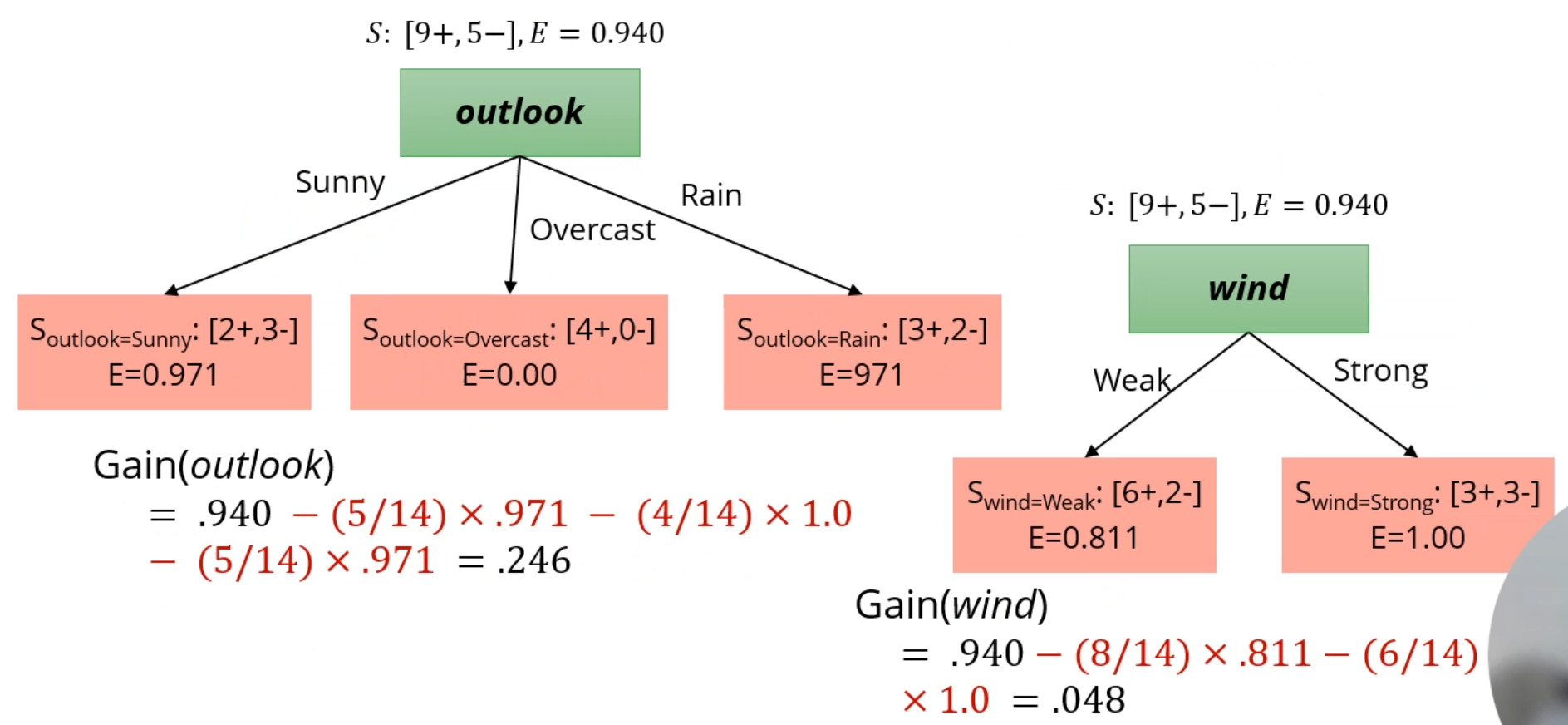
아까 Outlook, Temp, Humidity, Wind의 attribute가 존재했습니다.
Temp와 같은 방식으로 연속형 값에 대한 최적의 기준을 Wind에서도 찾고,
이 Attribute들로 생성되는 IG를 비교해줍니다.
IG는 outlook이 기준일 때 제일 높네요. 첫 분류기준은 Outlook이 되겠습니다.
또한, C4.5의 또다른 개선법은 IG 계산의 정교화입니다.
기존의 IG 계산법은 Node를 많이 쪼개는 Attribute가 유리했습니다.
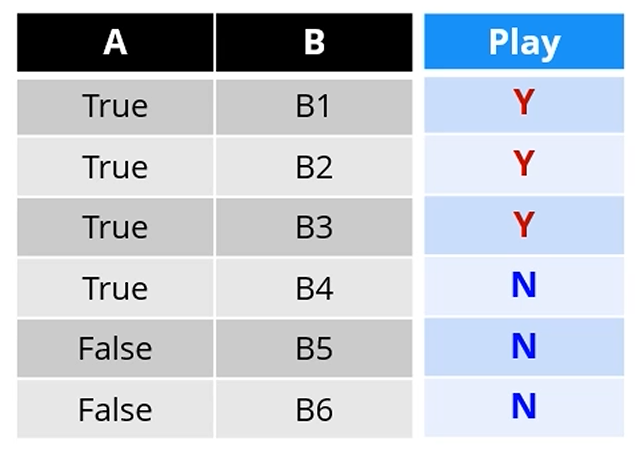
A는 2개로만 쪼개지만, B는 6개로 쪼개네요.
B를 기준삼으면 뭘 기준으로 잡건 Entropy가 0이 됩니다.
이걸.. 좋은 Entropy로 잡을 수는 없죠.
기존의 IG 계산식에 따르면 B를 기준삼으면 Information Gain이 최대가 됩니다.
GainInfo
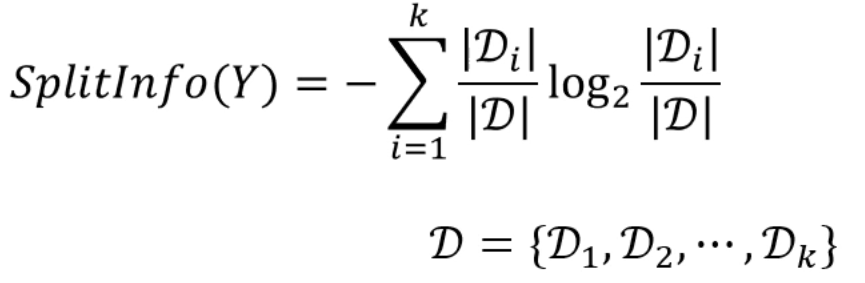
다음과 같은 공식이 등장합니다.
분류되는 결과의 구분도를 가지고 Gain을 정의하는 것은 똑같은데,
분류되는 결과의 절대크기 역시 Gain 계산에 포함을 시킵니다.
위의 SplitInfo 식은 Entropy 식과 매우 유사하게 생겼습니다.
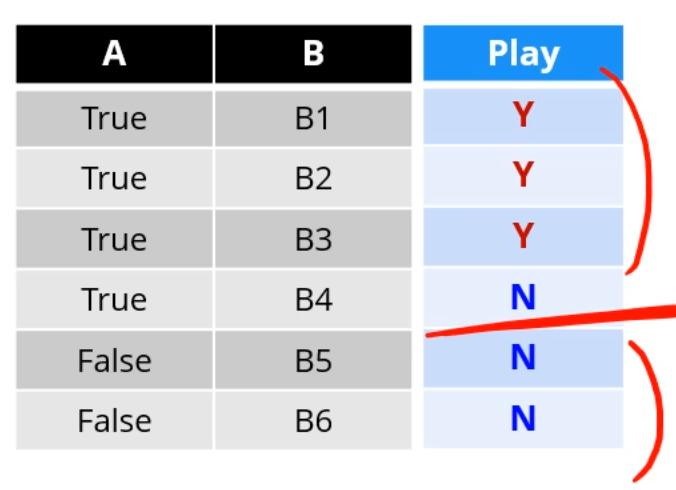
앞선 데이터셋을 A로 쪼개면 4개 / 2개로 쪼개집니다.
B로 쪼개면 1개 / 1개 / 1개 / 1개 / 1개 / 1개로 쪼개지구요.
이를 이용해 SplitInfo(A), SplitInfo(B)를 계산합니다. (쪼개진 결과는 여기선 관련이 없습니다)
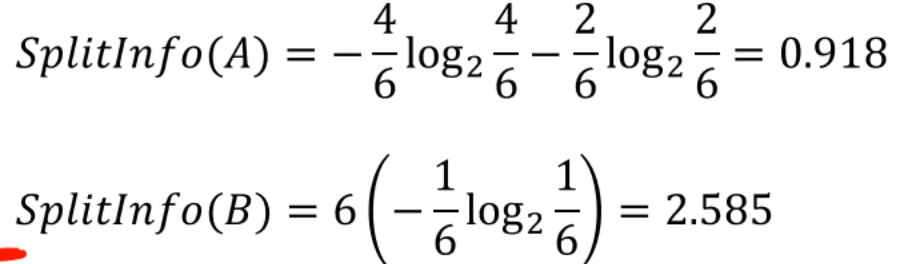
A는 6개가 4개/2개로 쪼개졌고, B는 6개가 1개/1개/1개 ...로 쪼개집니다.
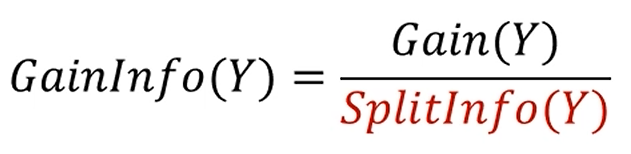
그리고, 각각의 SplitInfo를 분모로 Gain을 나눠주면 GainInfo가 완성됩니다.
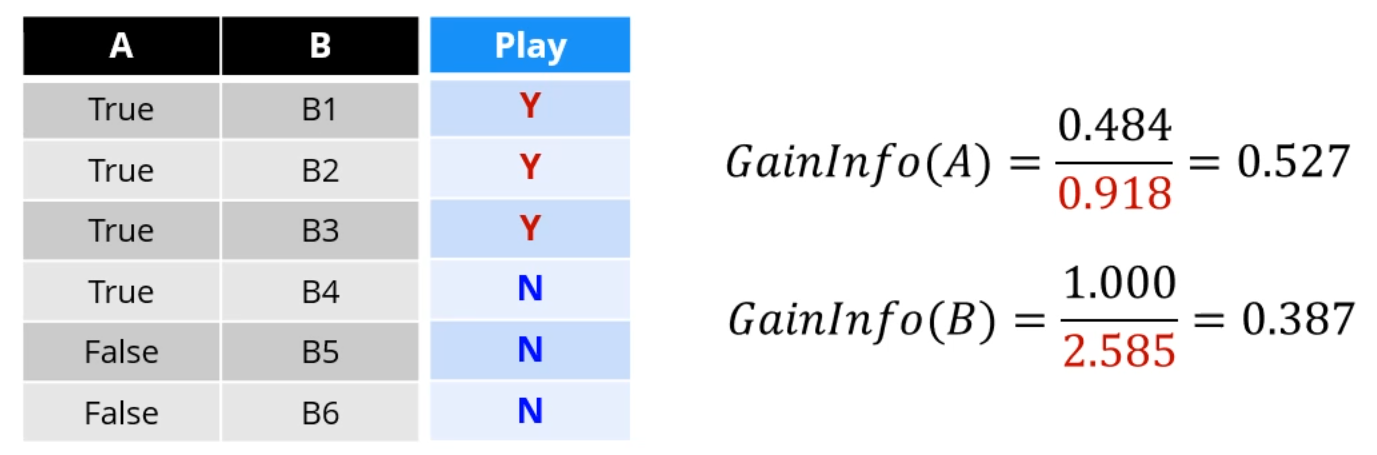
GainInfo 없이 Gain만 놓고 보면 무식하게 모든 데이터가 각각의 node로 분류된 B가 훌륭한 기준이지만,
나눠진 sample들의 개수까지 고려를 하니 B보다 A가 더 좋은 attribute로 보이게 되는거죠.
Missing Infos
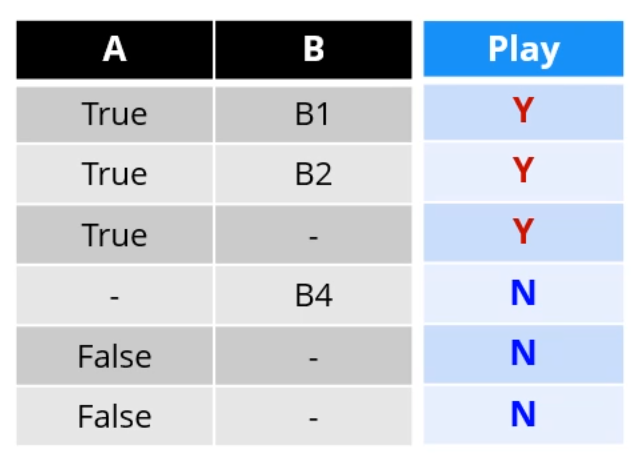
몇몇 데이터가 빌 수도 있죠.
단순히 Entropy만 계산할 때에는 non-missing value만 씁니다.
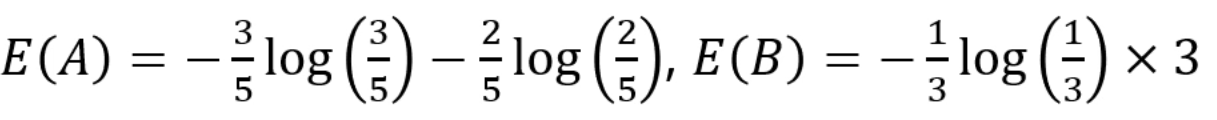
A가 기준이면 5개 중 3개가 True, 2개가 False고,
B가 기준이면 3개 중 1개가 B1, 1개가 B2, 1개가 B4네요.
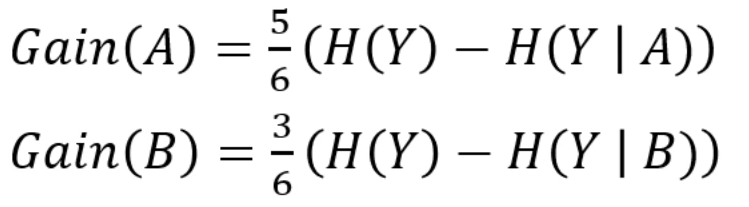
그 Entropy를 이용해 구하던 Gain은, 부모 값에서 빼주는 건 맞지만,
결측치 개수만큼의 가중치가 들어갑니다.
결측치가 많으면 점수가 까인다고 생각하시면 돼요.
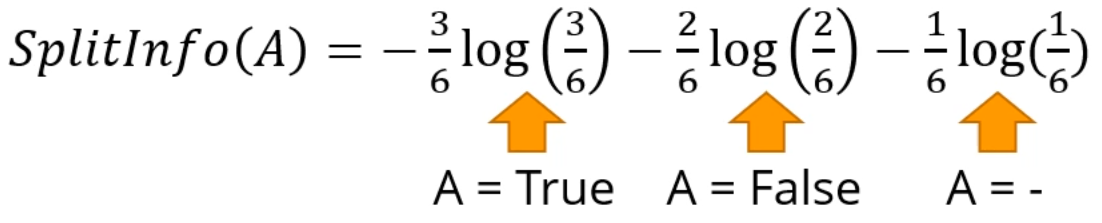
마지막으로 SplitInfo는 Missing Value까지 새 class로 가정하여 계산합니다.
그러면 Entropy를 이용해 Gain이 구해지고,
Gain과 SplitInfo를 이용해 GainInfo가 구해지니
결국 결측치를 완전히 포괄하는 계산법이 되었네요.
CART (Classification And Regression Trees)
CART는 Classification / Regression Tree를 만드는 방법을 통칭합니다.
C4.5와 매우 흡사한데, 조금 다릅니다.
CART는 Entropy 대신 GINI Index를 사용합니다.

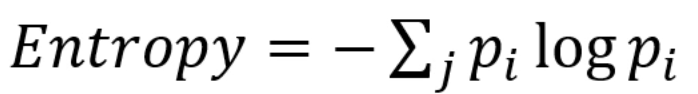
둘의 비교가 되죠.
각각의 확률의 제곱의 합을 더해서 1에서 빼주면 GiniIndex가 됩니다.
Entropy처럼 0일 때 제일 Pure한 데이터입니다.
또 다른 차이점은, 조금 큰 차이점인데,
CART는 무조건 Binary Split만 지원합니다.
가령 Attribute가 Days : Mon, Tue, ~~ Sun이었으면,
ID3, C4.5는 Days를 기준으로 쪼개면 7개의 branch가 나오는데,
CART에서는 한번 쪼갤 때 무조건 Binary로 쪼개집니다.
가령 {Monday} vs {Not Monday}나, {Mon, Fri} vs {Others} 처럼요.
또, CART에선 attribute가 특정 값일 때의 gain을 계산합니다.
Gain(Income = Low), Gain(Income = High) ... 처럼요
CART - Regression Tree
Regression Tree에선 각 node의 출력을 다음과 같이 정의합니다.
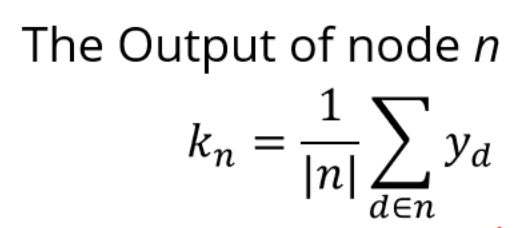
Error는 다음과 같이 정의되구요.
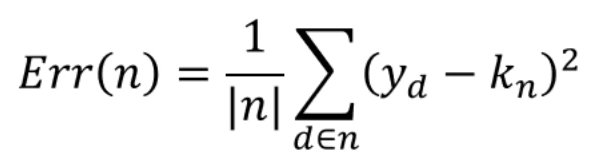
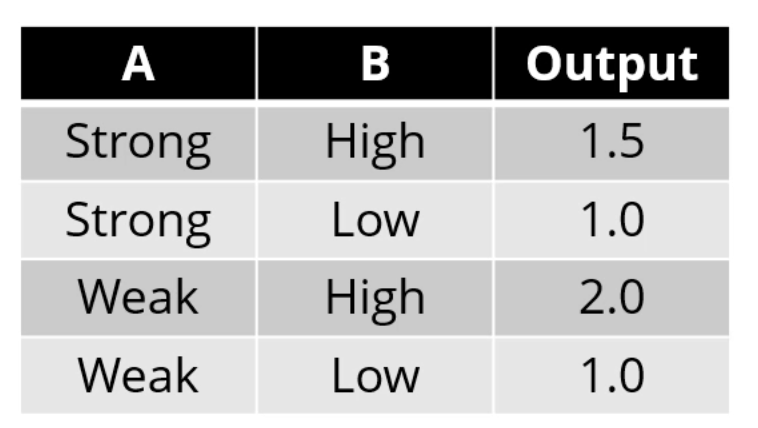
예시를 들어 보는게 제일 확실합니다.
[A]를 기준으로 쪼개봅시다.

이러면 [Strong] side의 출력은? 1.5와 1.0의 평균인 1.25로 정의되구요,
[Weak] side의 출력은 1.5로 정의되네요.
그러면 Strong side의 Error는 MSE (Mean Squared Error)를 이용하니, (0.25)^2 + (0.25)^2 = 0.125,
Weak side의 Error는 (0.5)^2 + (0.5)^2 = 0.5가 되구요.
결국 A로 쪼갰을 때의 Error는 0.125 * 2/4 + 0.5 * 2/4 = 0.3125가 됩니다.
[A]라는 attribute가 갖는 값은 0.3125네요.
CART Regression Tree에선 Gini Index 대신 MSE를 이용하여 Attribute를 평가합니다.
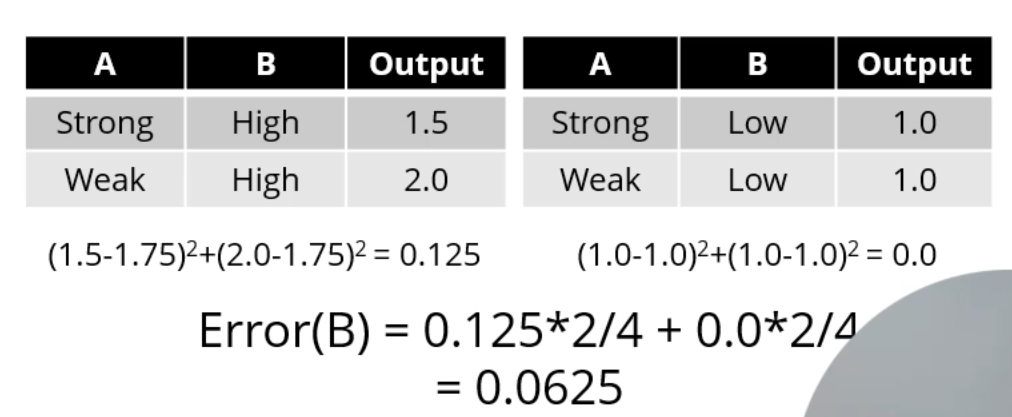
[B]라는 Attribute로 쪼갰더니 Error가 0.0625가 되었습니다. 얘가 훨씬 좋네요.
Decision Tree - Depth
Tree의 깊이를 너무 제한하면 Underfitting이,
Tree의 깊이를 너무 풀어주면 Overfitting이 발생합니다.
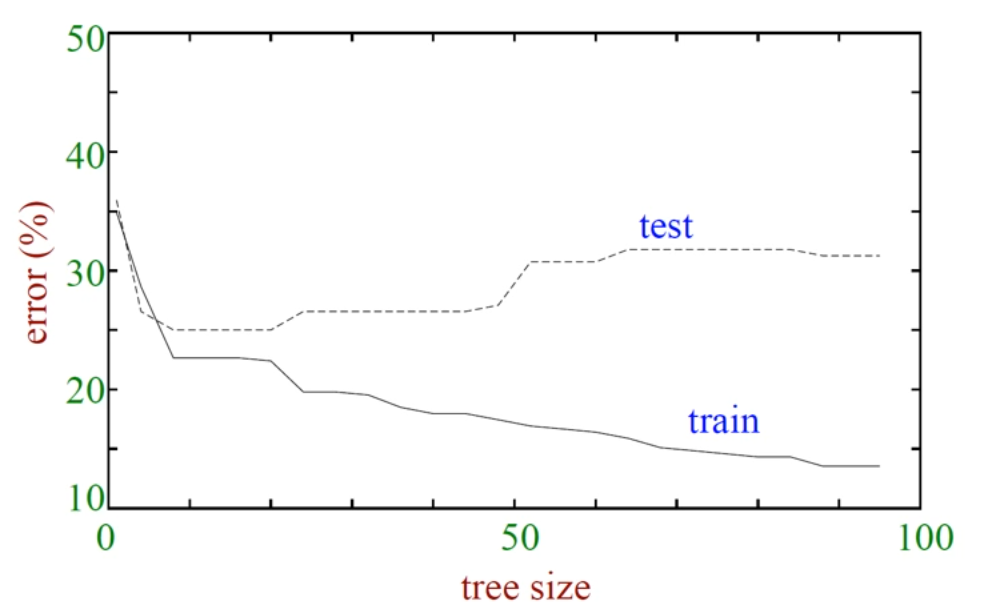
Tree size가 너무 작으면 error가 너무 크구요.
Tree size가 너무 커지면 trianing data는 잘 분류하지만 test data에서 error가 너무 늘어나네요.
PrePruning
IG가 특정 threshold보다 낮으면, 그냥 더 자르지 않습니다.
자르면 이득이겠죠. 근데 Overfitting 쪽으로 더 갈 수도 있어요.
이걸 Prepruning이라고 합니다.
Postpruning
일단 아주 세세하게 분류한 다음, 특정 가지를 쳐냅니다.
