지금까지 배운 것은 전부 지도학습이었습니다.
정답이 있고, 분류를 하고 오차를 찾는 것이었어요.
Clustering은 Unsupervised Learning입니다.
문제만 주어지고, 답은 없습니다!
하지만 여기서 패턴을 찾는 것이 비지도학습의 목표인 것이죠.
data instance들이 주어졌을 때, 비슷한 군집을 찾는 것이 clustering입니다.
물론 군집에 정답이 있을 수는 있죠.
하지만 우린 그런거 모른다고 가정하고, 입력 벡터만 보고 가까운 벡터끼리 뭉치는 작업을 합니다.
Clustering
What is clustering?
'같은 군집의 애들은 좀 비슷하고', '다른 군집은 좀 안 비슷하게'끔 묶는 것입니다.
그걸 위해서는 역시 '유사도'를 측정할 방법을 정의해야하겠죠.
Label되어있지 않은 data를 group (cluster)로 나누고 싶습니다.
그리고 각 cluster는 유사해야 합니다.
Clustering에서는 2가지가 중요합니다.
1. 같은 class들끼리는 비슷해야 합니다. (High intra-class similarity)
2. 다른 class들끼리는 달라야 합니다. (Low inter-class similarity)
그렇다보니, clustering 방식은 유사도 measure에 따라서 크게 달라집니다.
정말 큰 dataset에 대해 overview를 얻고 싶다면,
dataset에 clustering을 수행한 후 cluster중 일부 샘플만 뽑아서 overview를 얻을 수 있습니다.
이런 경우에 clustering이 유용하게 쓰이죠.
아니면, data를 직접 구분하는 것이 too expensive하다면 역시 clustering이 필요해집니다.
혹은 결측치를 찾는데에도 좋습니다. 어느 cluster에도 속하지 못하는 애가 있다면 outlier겠죠.
Various clustering approaches
Clustering을 나누는 4가지의 기준이 있습니다.
- Partitioning Criteria
만들어진 클러스터가 같은 계층의 cluster인지, (single-level)
cluster간의 계층이 존재하는지에 따라 나눌 수 있습니다. (Hierarchical Partitioning)
- Separation of Clusters
하나의 튜플이 하나의 클러스터에만 속할 수도 있고, (Exclusive)
하나의 튜플이 여러 클러스터에 속할 수도 있습니다. (Non-exclusive)
- Similarity Measure
Distance-based (Euclidian..)으로 바로 유사도를 측정할 수도 있고,
Connectivity-based로 주변 맥락까지 고려하여 유사도를 측정할 수도 있습니다.
- Clustering Space
Full Space를 써서 clustering이 일어날 수도,
Full Space에서 Subspace를 써서 Clustering이 일어날 수도 있습니다.
Flat vs Hierarchical Clustering
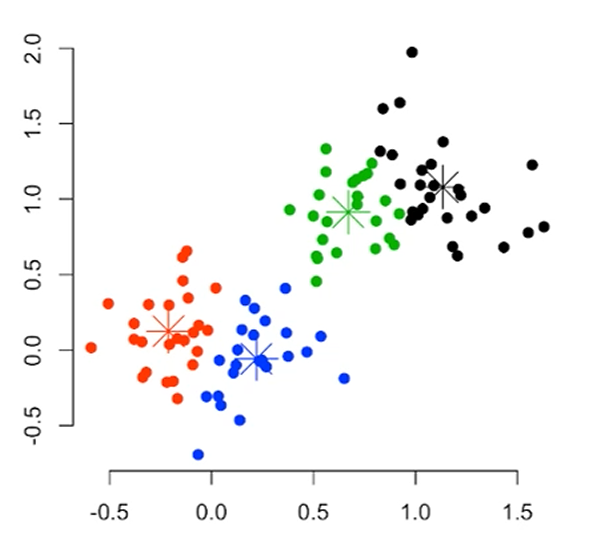
이렇게 분류되면, 그냥 flat한 single-level clustering이고,
(K-means, K-medoids)
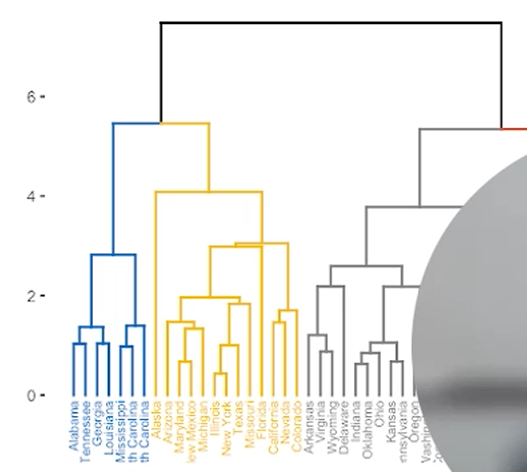
이런 식으로 분류되면 Hierarchical Clustering이 됩니다.
(DIANA, AGNES, BIRCH, CAMELEON ...)
보통은 Bottom-up 방식 (agglomerative) 을 많이 사용합니다.
Objective Function
이렇게 많은 clustering algorithm들이 추구하는 부분을 수학적으로 표현을 해보면,
Dataset 이 있을 때,
이 dataset을 k개의 cluster group 로 구분할 것입니다.
각 Cluster 의 중심 (Centroid)를 로 칭하겠습니다.
이 때, 전체 Dataset의 Error를 다음과 같이 정의합니다.
즉, Cluster j에 속한 모든 data에 대해, centroid 와의 오차를 로 정의하고,
그 오차의 합을 Cluster 의 오차로 두며,
모든 Cluster에 대해 그 오차들을 더하면 Dataset 의 Error합이 되는 것이죠.
물론 한계점이 보이죠? 우선 k를 우리가 정의하는 것도 어색하구요,
Exclusive한 dataset을 가정했구요.
는 조상님이 정해주십니까?
하지만 대략적인 개관은 이 공식으로 확인이 가능해집니다.
물론, Instance를 Cluster에 매핑하는 방법은, Cluster가 k개, instance가 N개 있을 때
이 됩니다.
그 중에서 optimal한 solution을 찾는다? 이건 NP-Hard한 문제입니다.
우리는 Heuristic한 solution을 찾을수밖에 없게 되죠.
K-means clustering
가장 기초적인 clustering 알고리즘입니다!
세련된 알고리즘은 아닌데, 간단하게 clustering을 수행할 수 있습니다.
는 사용자가 직접 정합니다. Euclidian space를 보통 가정하구요.
우선, k개의 random sample을 각 cluster의 중심으로 잡습니다.
그 후, 각각의 sample들이 가장 가까운 centroid에게 가서, 할당이 됩니다.
그럼 이제 Cluster마다 원소들이 모였겠죠.
그 후, 그 멤버들 간에 centroid를 새로 잡습니다.
이걸 계속 반복하면 centroid 위치가 수렴합니다.
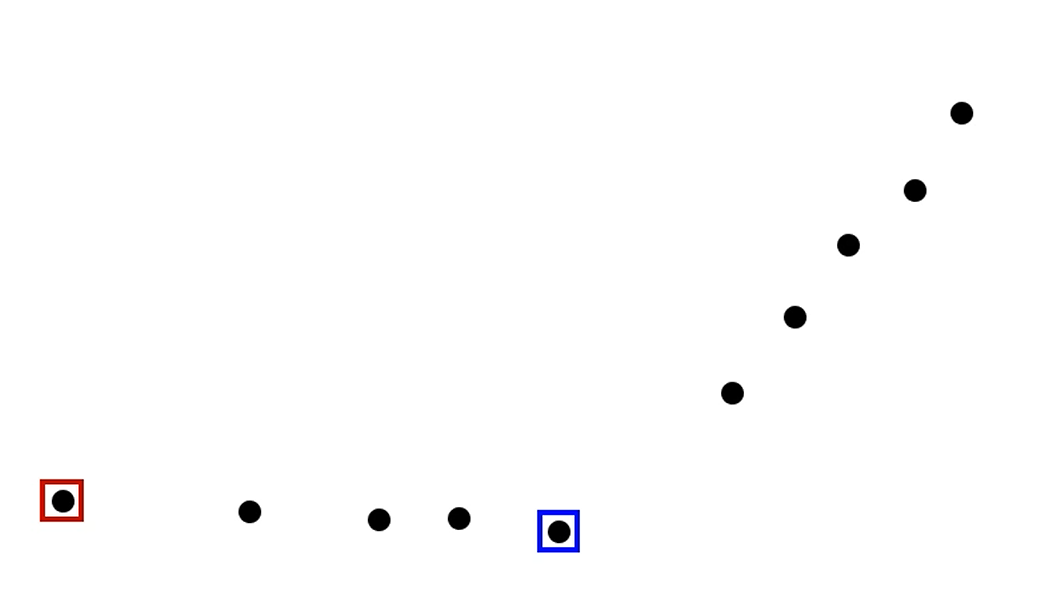
k=2라고 할 때, 랜덤하게 2개를 centroid로 잡습니다.
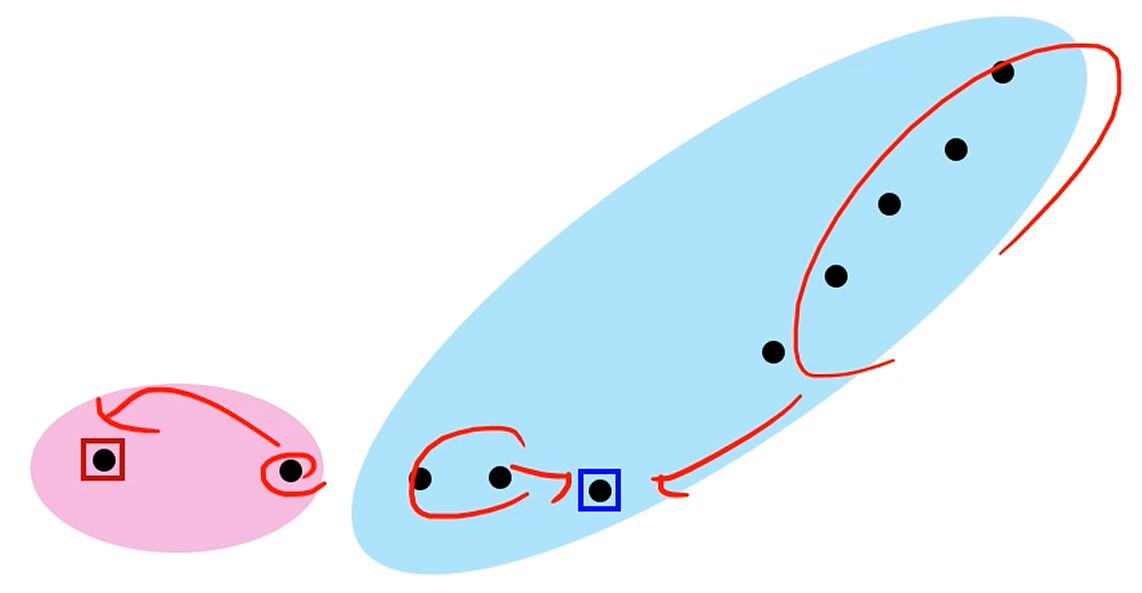
가장 가까운 centroid와 같은 cluster가 되게 묶어주고,
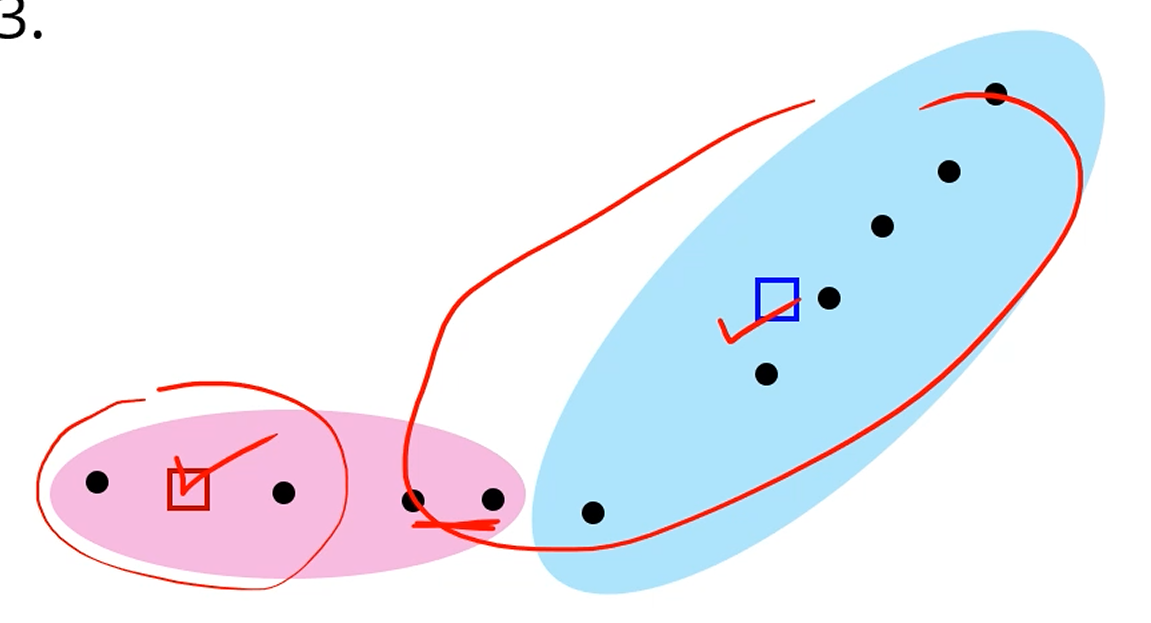
새 centroid를 다시 계산하고, 재 분류를 하고,
이걸 centroid가 수렴할 때까지 반복합니다.
시간복잡도는, 입니다.
는 centroid 개수, 은 데이터 개수, 는 iteration 수행 횟수입니다.
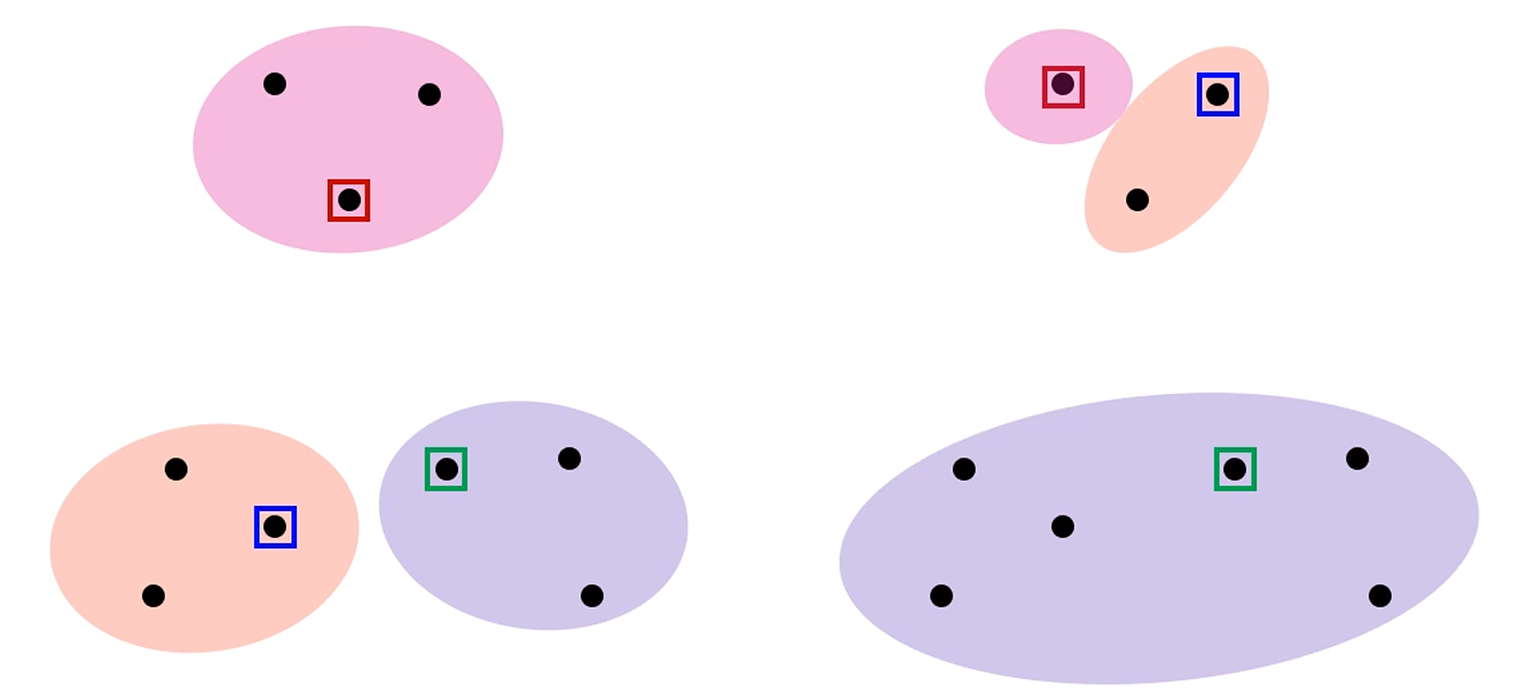
근데, 직관적으로 보이지만,
어떤 sample을 centroid로 잡냐에 따라서 clustering의 결과가 달라지겠죠.
그래서 K-means algorithm은 도 중요한데, 첫 centroid의 선정도 매우 중요합니다.
그래서 multiple starting points에서 수렴을 시도해보는 것이 매우!! 중요합니다.
k-means++같은 경우에는 첫 random point를 잡고 제일 먼 놈을 그 다음 random point로 잡고,
거리가 제일 먼 놈을 다시 그 다음 centroid로 잡고.. 이렇게 centroid를 설정하기도 합니다.
최대한 centroid끼리 떨어져서 초기 cluster를 잘 할당하게끔요.
How to choose k?
는 뭐 어떻게 여러번 시도해서 정한다고 칩시다.
는 누가 정해줍니까?
k를 점점 늘려가면서, 전체 점들의, 각자의 centroid로의 평균을 내서, 그 값을 잽니다.
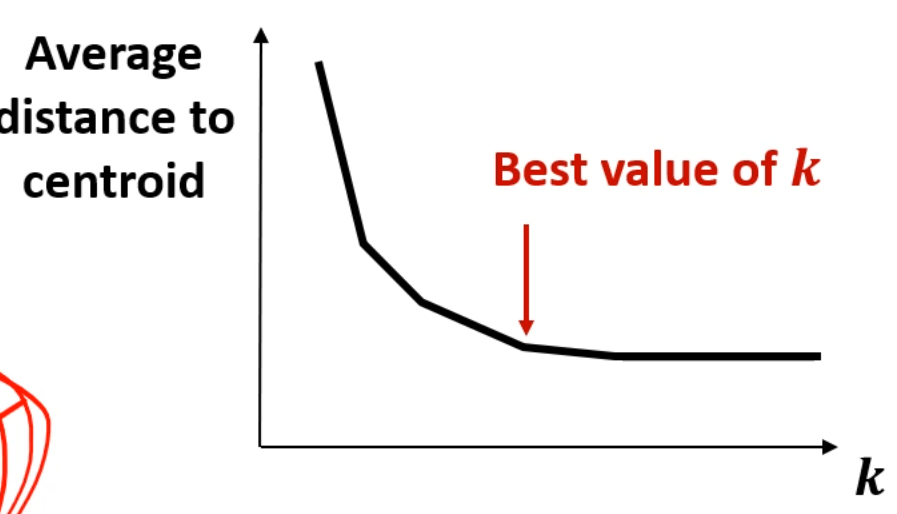
어느 순간부터 k의 감소량이 완만해지는데,
그 순간을 Best k로 잡는 Heuristic한 방식입니다.
Summary of K-means clustering
정리를 하면, 간단하고 효과적인게 장점입니다.
을 갖긴 한데, 병렬화가 매우 잘 되는 알고리즘입니다.
그래서 실전에선 n이 엄청 크더라도 사용이 가능합니다.
또, 거리를 잴 때도 벡터간의 거리를 재야 하는데,
CPU나 GPU에서 벡터 산술연산은 엄청 빨리 되게끔 지원을 합니다.
단점으로는 를 잘 골라야 한다는 점,
local optima에 취약하다는 점,
outlier에 민감하다는 점이 있습니다.
outlier를 잡기 위한 대체 방식은 connectivity 방식이 있겠네요.
Bisecting k-means
hierarchical 한 k-means 알고리즘입니다.
처음엔 k=2로 cluster를 쪼개고,
그 cluster들을 다시 개별의 cluster로 간주하고, 필요에 따라 다시 2개로 쪼개는 겁니다.
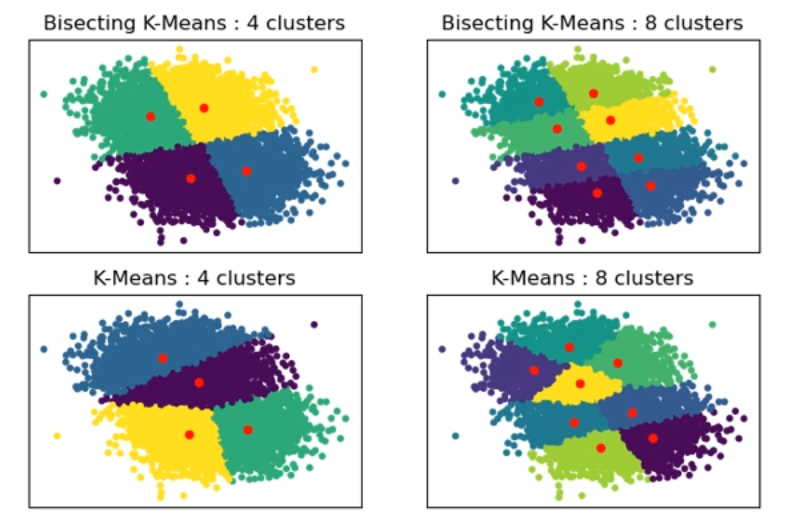
결과가 좀 대칭적으로 나오죠?
조금 계층적인 답이 나옵니다.
어떤 cluster를 반으로 쪼갤까요?를 생각해보면,
data point가 가장 많은 cluster를 반으로 쪼갤 수도 있고,
중심으로부터 떨어진 분산이 큰 cluster를 반으로 쪼갤 수도 있습니다.
아무튼 이건 정하기 나름입니다.
중요한건, 전체 하나의 cluster로 시작하여 반씩 쪼개어 나가며 계층을 만드는
그런 알고리즘입니다.
장점은, 각 clustering을 수행할 때마다 n이 절반으로 줄어드는 효과가 나게 됩니다.
빨라져요.
n=100짜리를 반으로 띡 쪼개면,
그 다음 cluster를 반으로 쪼개려고 보면 n=50만 놓고 보면 되는거죠.
Full Space가 n=50으로 줄어든겁니다.
근데 사실 잘 안써요 ㅎㅎ

이런 이미지들도 픽셀의 값을 이용해서 k-means를 이용해서 쪼갤 수 있습니다!
같은 종류의 사물을 같은 식으로 자동으로 칠한 모습이에요.
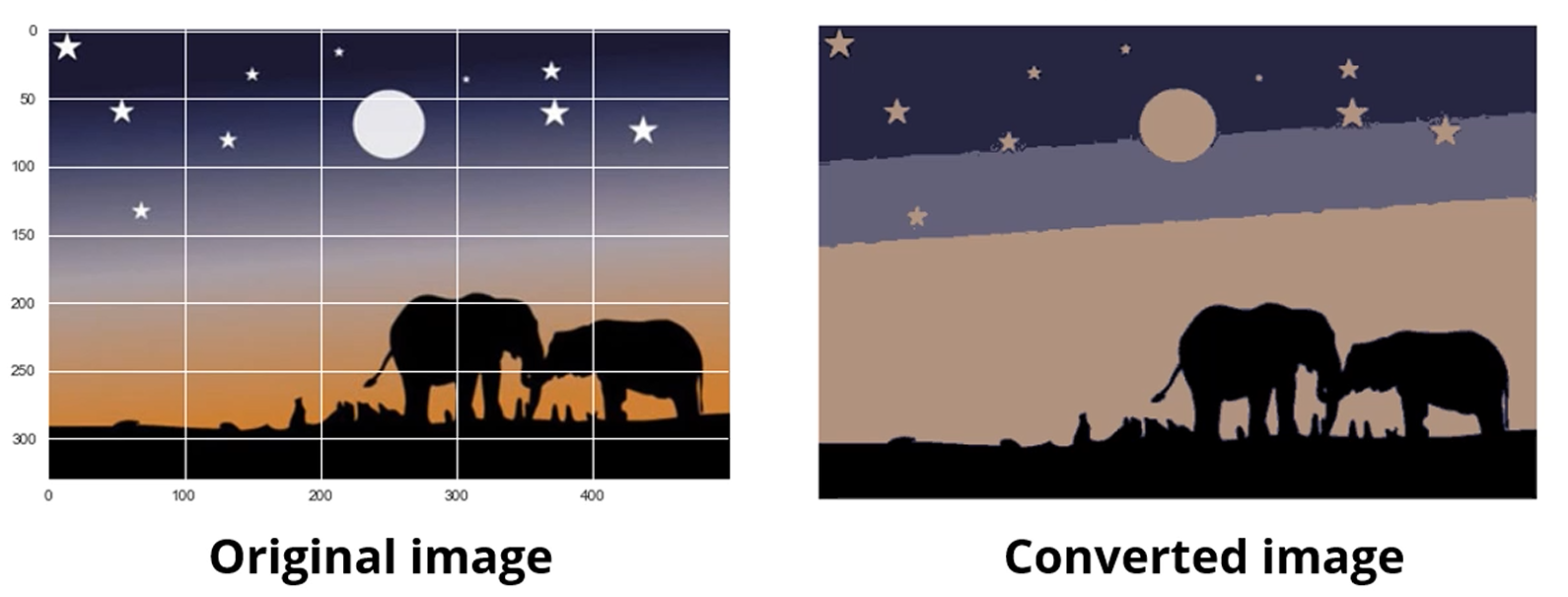
이것도 original image에서 모든 픽셀 color를 다 뽑아서, k=4인 k-means를 수행한 모습입니다.
비슷한 색상들은 하나로 cluster되겠죠.
멋지네요.
지금도 대표색을 뽑는 경우에는 k-means를 많이 씁니다.
군집의 centroid를 대표색으로 잡으면 되니까요.
Generative vs Discriminative
좀 갑작스러운데, 다시 분류 얘기로 돌아와봅시다.
분류기를 만들면, generative한 분류기와 discriminative한 분류기가 존재합니다.
Discriminative Neural Network들은 내부적으로 , 즉 입력 이 주어졌을 때,
그 입력이 중 하나일 확률을 모델링한 그런 모델을 따릅니다.
즉, 입력이 주어졌을 때 고양이일 확률 같은 모델을 한거죠.
즉, 새로운 입력 x를 생성하는 능력은 없습니다.
입력 x를 구분할 수는 있어도요.
우리가 x를 생성하기 위해서 알아야 하는 건,
어떤 'class'가 주어졌을 때,
그 class에서 특정 X가 관찰될 확률, 즉
를 알아야 합니다.
그래야 'cat' 내에서 'picture'를 생성할 수가 있어요.
베이즈 정리
에서, (분모는 생략합니다)
Discriminative model들은 만 알고 있는거고,
Generative model들은 를 알고 싶은 거니까,
걔네는 추가적으로 , 즉 입력 데이터의 사전분포 역시 알고 있어야합니다.
Clustering의 맥락을 끌어오면,
K-means에서는 어떤 data가 주어지면 그 데이터가 '지금까지 찾은 centroid 중 와 제일 가까워요! 그래서 얘는 에 속해요'라는걸 해줍니다.
근데, '야, 그러면 에 속하는 새로운 를 만들어봐.'라는 명령을 수행할 수 없게 됩니다.
근데,
K-means를 조금만 바꾸면,
우리는 cluster가 주어졌을 때 cluster에 속하는 임의의 x를 생성해 낼 수 있습니다.
GMM (Gaussian Mixture Model)
가우시안 모델을 Mix한 모델입니다.
엄밀히 말하면 Clustering 모델은 아닙니다.
근데 Clustering에 '쓸 수' 있습니다.
가정을 해봅시다.
전체 데이터는 k개의 gaussian 분포로부터 왔습니다.
그래서, 우리가 가 관찰될 확률은,
각각의 data instance들이 라는, 각각의 Gaussian Distribution을
기술하는 parameter를 가지고 뽑힐 확률의 곱으로 나타내지게 됩니다.
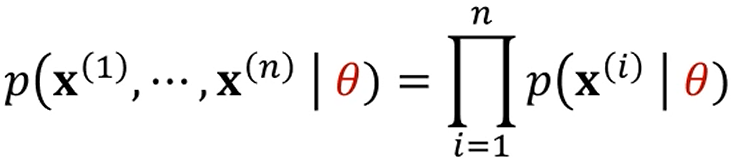
즉, n개의 data instance는 k개의 gaussian distribution으로부터 독립적으로 생성되었고,
그 gaussian distribution들을 나타내는 매개변수가 인데,
를 기준으로 이 생성될 확률은
를 기준으로 이 생성될 확률과, 가 생성될 확률과, ... 의 곱이라는 거죠.
그러면 )는 어떻게 계산하나요?
우리가 Gaussian 분포에 대한 pdf를 알고 있기 때문에, 단순하게 표현이 가능합니다.
즉, 정리하면
눈에 보이지 않지만, 존재하는 Latent한 k개의 gaussian 분포가 있고,
그 k개의 gaussian 분포의 parameter 를 찾는 것이,
원래의 데이터를 Gaussian mixture model로 모델링하는 과정이 됩니다.
그래서 몇 개의 gaussian model이 존재하나요?
k=1이라면, 뭐 별로죠.
하나의 분포로부터 데이터가 다 왔다는건데, 별로 안 좋아요.
그래서 k를 여러 개 둡니다.
K-means에서는 cluster의 centroid를 계산하는 문제였습니다.
gaussian 분포도 중심인 가 있고, 가우시안 분포를 나타내기 위한 공분산 행렬 가 존재합니다.
즉, i번째 gaussian 분포는 를 파라미터로 가집니다.
에요.
근데 이 라는 놈이 centroid이기 때문에, k-means의 중심과도 연관이 생기게 됩니다.
하지만 결정적인 차이는, 가령 K=2일 때,
어떤 instance든 두 cluster 중 하나로만 할당이 됩니다.
극단적이에요.
가 각 cluster에 속할 확률은 1 또는 0입니다.
이렇게, 하나의 sample이 하나의 cluster에만 속할 경우를 Hard Asisgnment라고 부릅니다.
반대로, Sample이 cluster에 속할 확률이 이분적으로 존재하지 않을 경우,
즉 k=2인 경우 item이 cluster에 속할 확률이 (0.7, 0.3)처럼 나타나는 경우,
1번째 gaussian 분포로부터 왔을 확률이 0.7, 2번째 gaussian분포로부터 왔을 확률이 0.3으로 해석되는 거죠.
즉, 하나의 instance가 각 gaussian 분포에 속할 확률로 모델링 되는 경우,
Soft Assignment로 칭합니다.
Soft Assignment에서는, 각 instance에 대해
로 표현이 되고, 각 이 성립하며, 들의 합은 1입니다.
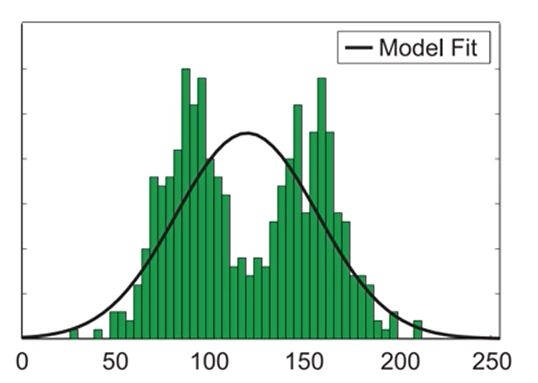
이렇게 밀도를 가진 데이터 (초록색)에 대해서, 하나의 Gaussian을 매핑한다고 하면,
그 분산을 최소화 시키는 gaussian 분포는 다음과 같이 나타내집니다.
data point의 평균이 gaussian 분포의 평균이 되고,
이 때 분산은 전체 데이터의 분산 를 삼으면 됩니다.
근데, 이 경우는 Bimodal한 data를 Unimodal한 gaussian 분포로 매핑했기 때문에,
잘 안 됐습니다.
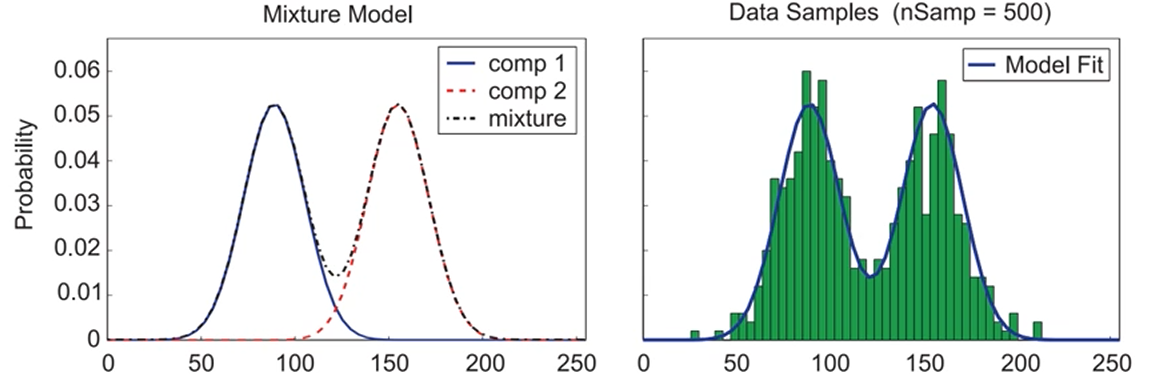
2개의 가우시안을 쓴다면,
bimodal한 데이터를 조금 더 잘 근사하는 분포를 그릴 수 있게 됩니다.
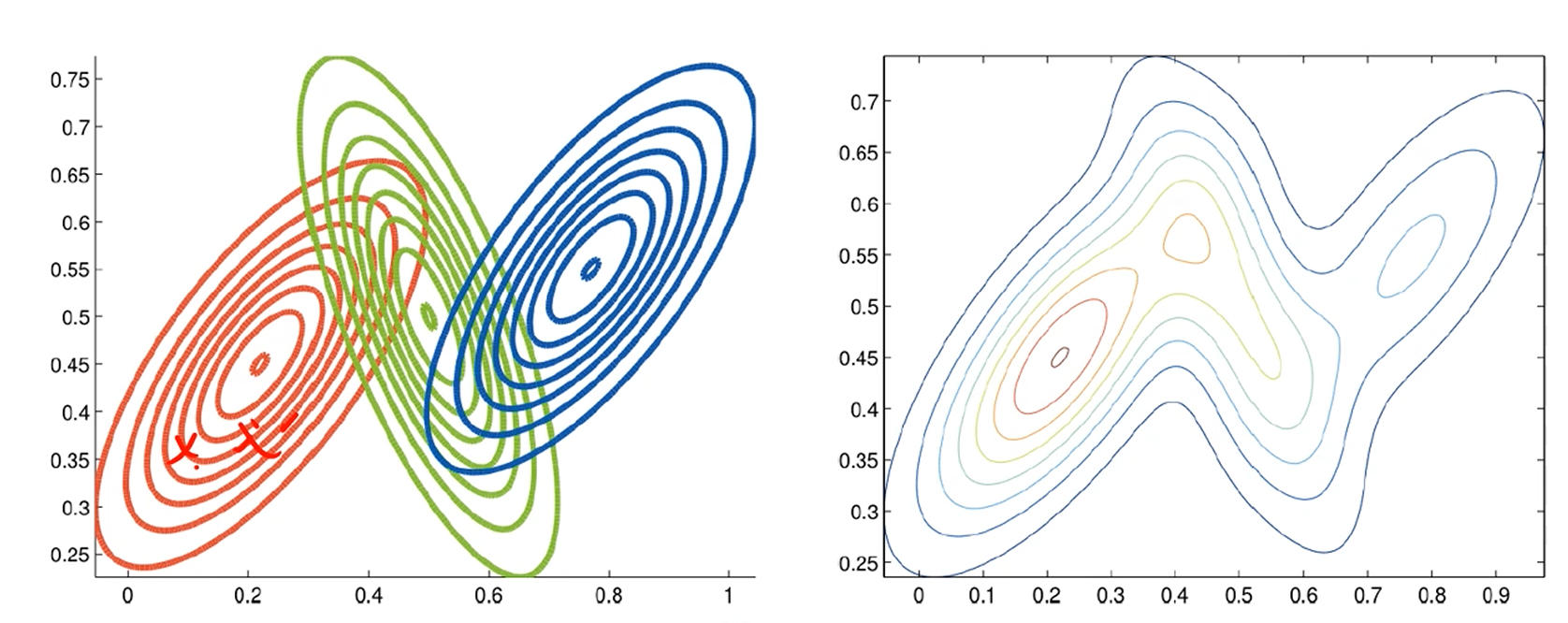
2차원의 경우도 수많은 점들을 3개의 가우시안으로 매핑이 가능해집니다.
그래서,
GMM에서는 데이터 분포를 k개의 gaussian 분포로 모델링하려고 합니다.
(Clustering은 일단 지금은 관련 없습니다.)
k개의 gaussian 분포는 각각의 중심 와 공분산행렬 로 표현이 됩니다.
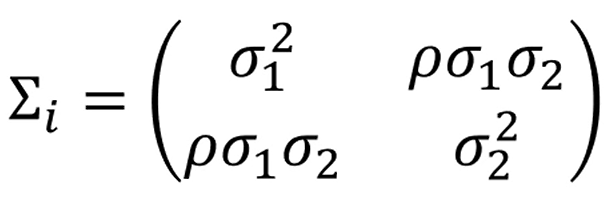
2개의 gaussian 분포가 존재한다면 각 gaussian 분포의 공분산행렬은 다음과 같이 정의됩니다.
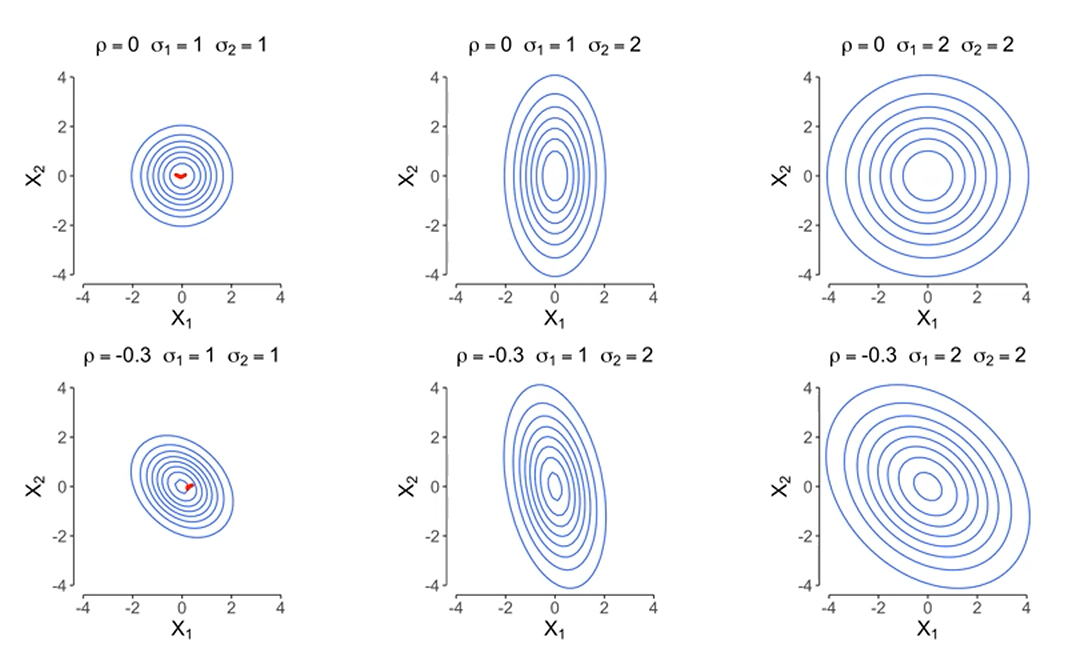
분포가 완전 원처럼 생겼다면, 는 로 표현됩니다.
그 외에도 데이터들의 상관관계에 따라서 gaussian 분포의 형태를 공분산행렬 로 나타낼 수 있습니다.
이라고 둡시다.
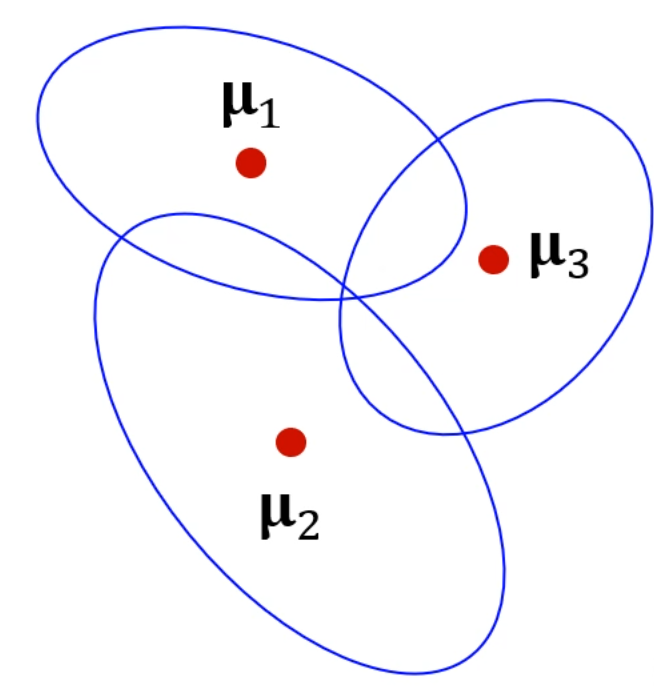
이렇게 3개의 가우시안 분포로 나타내지겠죠.
각각의 가우시안 분포는 같이 각자의 와 를 가집니다.
특정 데이터가 주어졌을 때, ()
그 데이터가 특정 cluster로 분류될 확률, 즉 가령
은, 로 표현할 수 있습니다.
마찬가지로 하고도 해당 data point가 분류될 확률을 계산할 수 있겠죠.

우리는 가 궁금합니다.
x가 관찰될 확률이 궁금해요.
그러면 이런 식으로 나타낼 수 있는데, 여기서 는 뭘까요?
특정 instance가 있는데, 그 특정 instance가 그 번째 gaussian 분포에서 왔을 확률입니다.
가령 뭐 총 10개의 데이터 중 7개를 1번째 gaussian 분포에서 끌어왔다면,
은 0.7이 되겠죠.
그리고 를 구하고 싶다면, 가 1번째 gaussian 분포에서 왔을 확률 * +
가 2번째 gaussian 분포에서 왔을 확률 * + ...가 됩니다.
그 각각 가 번째 gaussian 분포에서 왔을 확률, 즉 는 와 같은거구요.
Simplifying GMM
단순성을 위해 라고 둡시다.
즉, 차원간의 correlation이 존재하지 않아요.
그러면 가 되구요,
로 고정합시다.
MLE for GMM
와 를 모른다고 합시다.
그럴 때, 우리는 MLE를 이용해 그 값들을 알아냅니다.
로 둡니다.
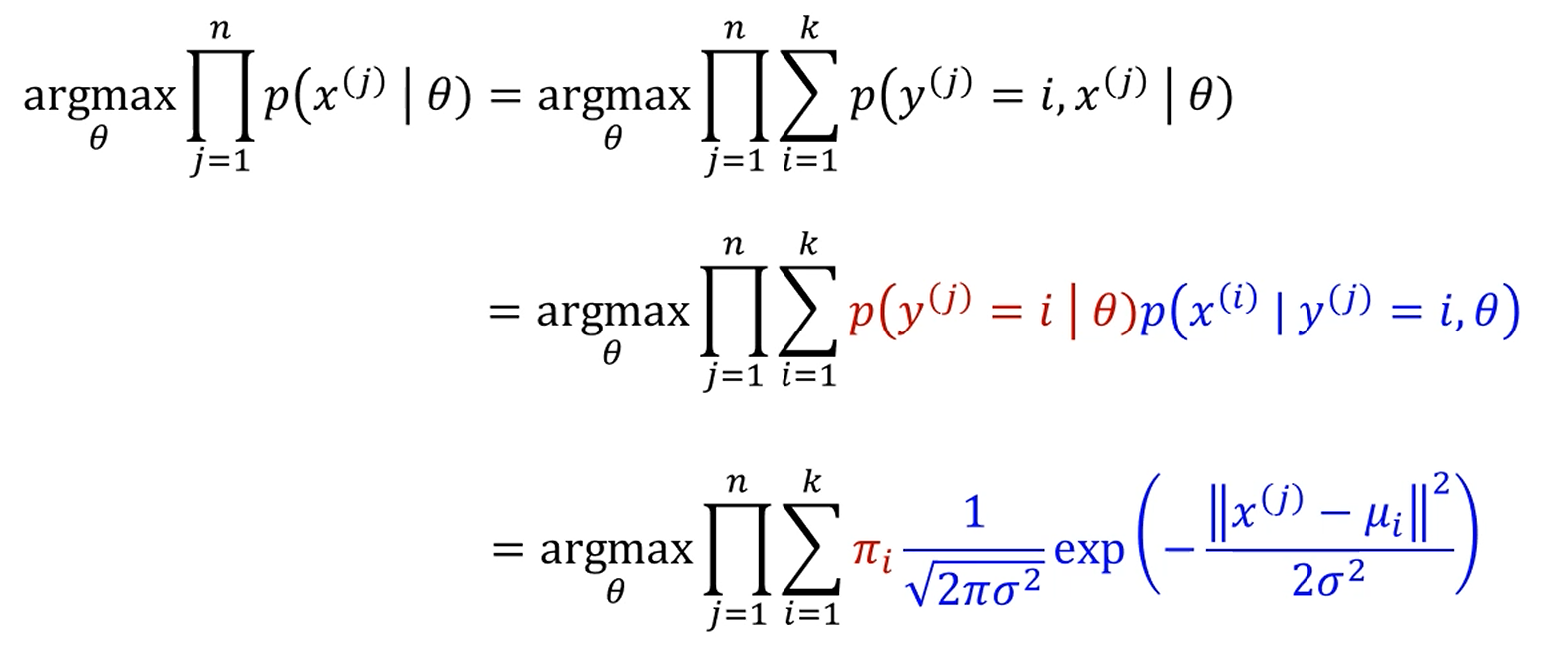
이 후 모든 data instance들이 parameter 하에서 나올 확률을 전부 곱한 값,
즉 맨 처음 나왔던 그 식을 구해봅시다.
이 확률은 각 data instance들이 각각의 cluster로 구분될 확률을 다 더한 것과 같죠.
는 조건부 확률을 이용해서 풀 수 있구요.
는 아까 정의했죠? 특정 class가 i로 분류될 확률. 였습니다.
는 어떻게 구할까요?
에, 라는 조건 하에서 가 구현될 확률이니,
해당 i번째 gaussian distribution의 pdf가 됩니다.
여기서 Hard Assignment의 가정을 넣읍시다.
즉, 가 앞선 경우처럼 로 나타나는게 아니라, 1 아니면 0입니다.
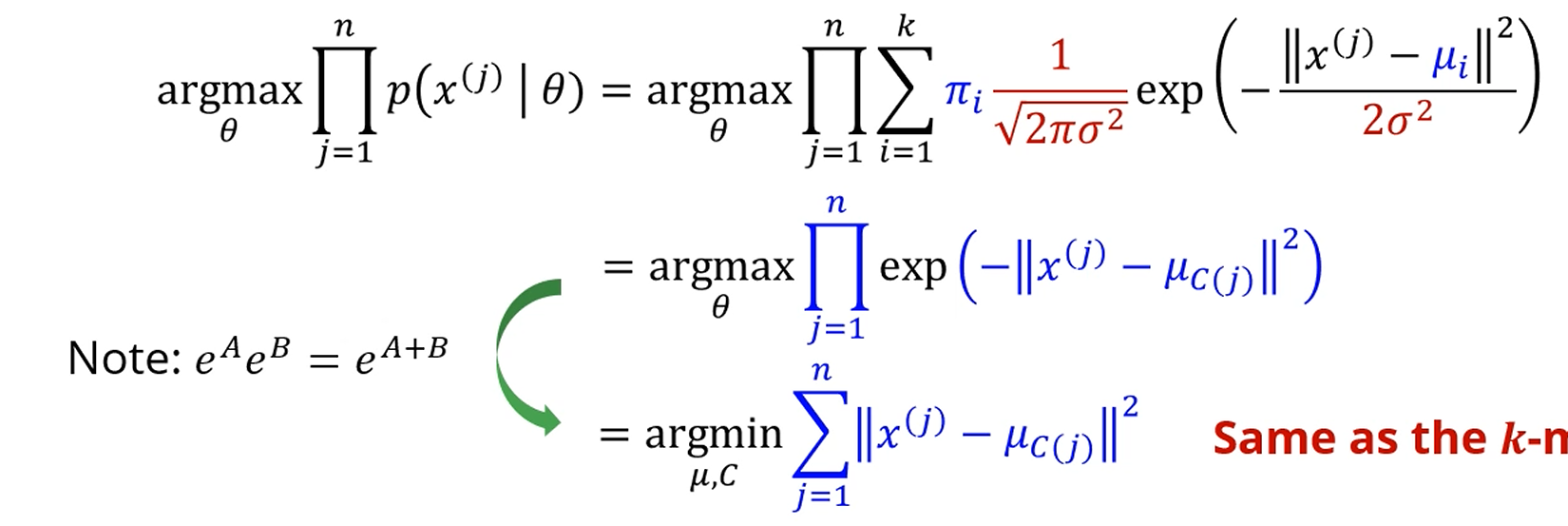
1 ~ k번째 cluster 중 해당 datapoint 가 속하는 유일한 cluster를 제외하면
는 전부 0입니다.
어차피 최대화하는 만 찾는게 목표이니 앞의 2 뭐시기는 다 날려도 되고,
를 전부 전개해서 덧셈으로 바꿔주면, 해당 값을 최소화하는 를 찾는 문제가 되네요.
어라?
와 cluster의 centroid 사이의 거리의 제곱 합을 최소화하는 를 찾는 문제가 됐네요?
오호! k-means네요!
즉, GMM에서 Hard Assignment를 가정하는 순간, GMM을 최적화 하는 것이 k-means를 푸는 것과 같은 문제가 됩니다.
좀 더한걸 가정해봅시다.
도 모르고, 도 모르고, 도 모릅니다. 다 모르네요.
앞에서는 그래도 는 알았는데요.
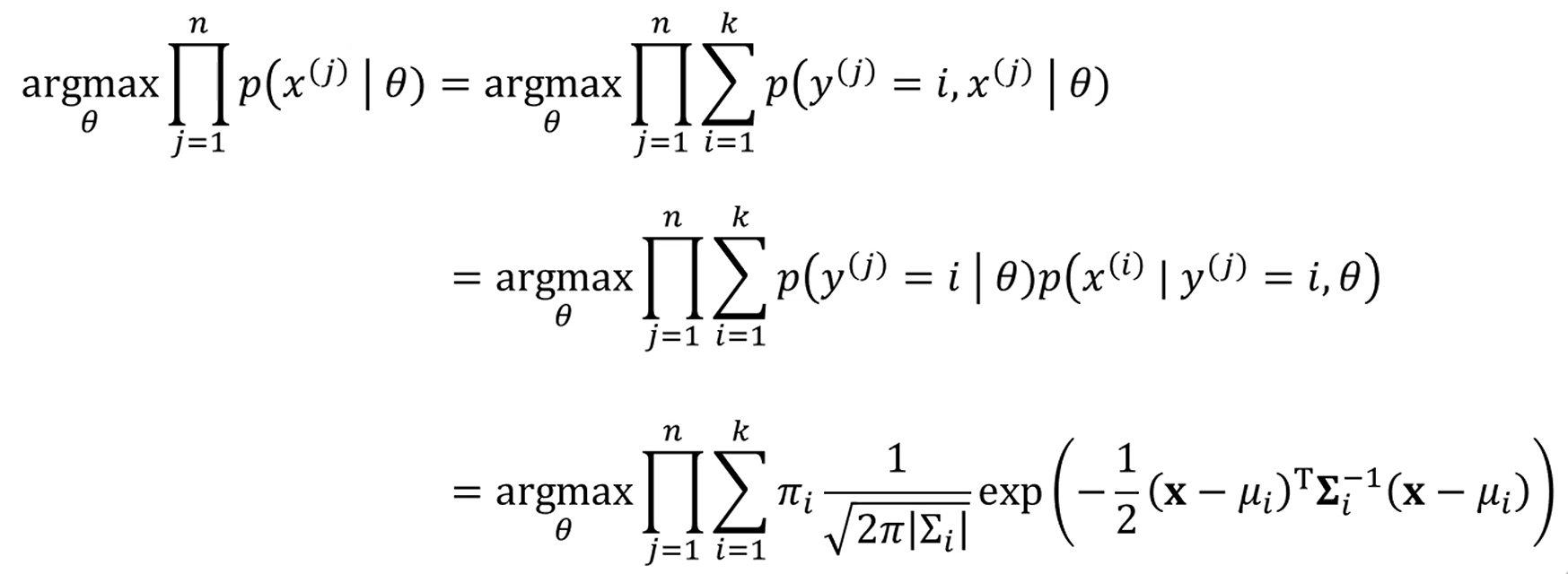
뚝딱뚝딱 해보면, 이 식을 최대화하는 를 찾아주면 됩니다.
Gradient Ascent를 수행해도 되는데, 느려터져서 보통은 EM 알고리즘이라는 걸 활용합니다.
EM Algorithm
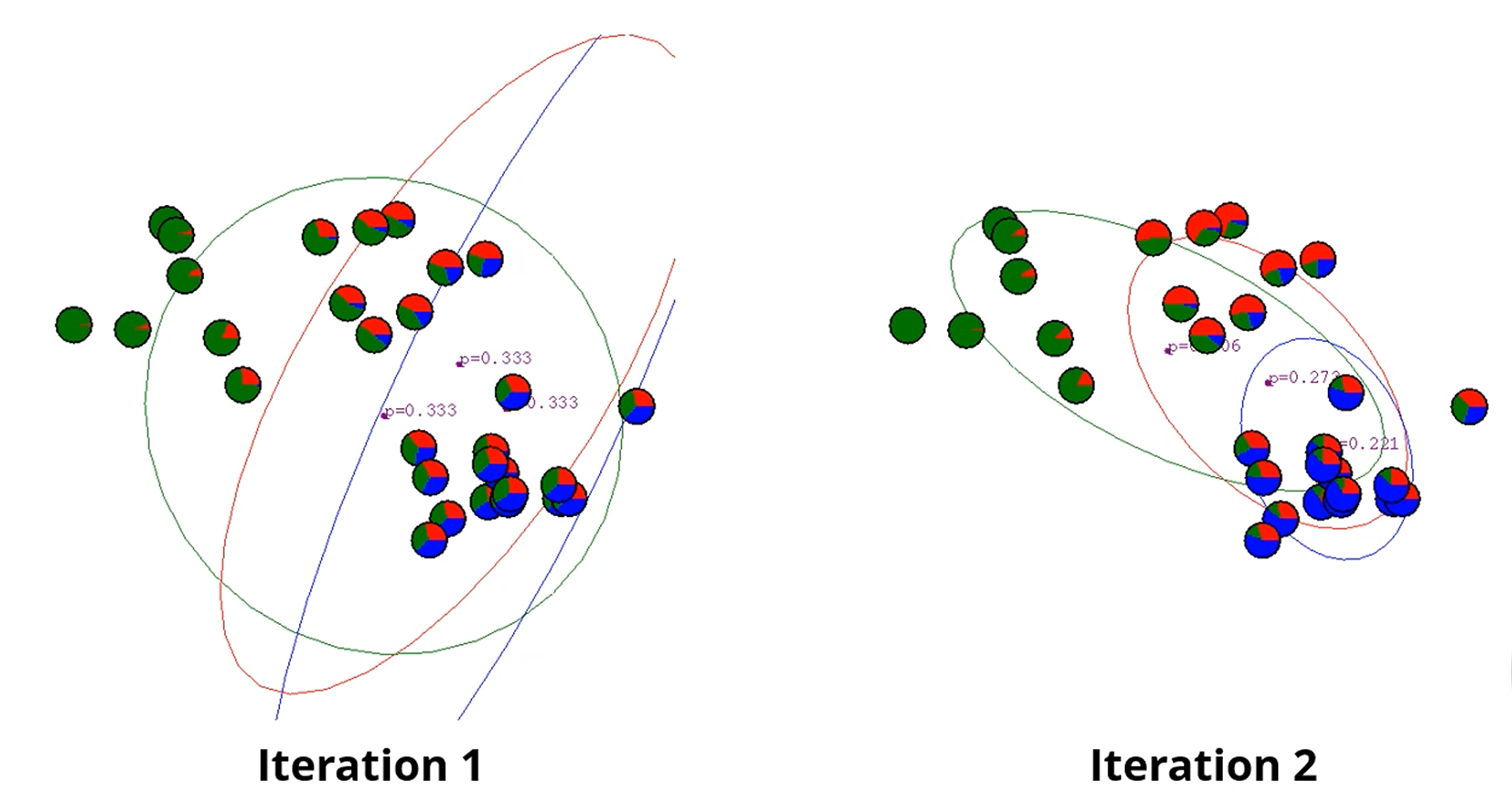
이런 점들에 대해서, 결국엔 3개의 Gaussian 분포의 중심과 공분산을 찾아야 하며,
각각의 점들이 어느 Gaussian 분포에서 왔을지도 알아야 합니다.
각 데이터 점들은 pi chart로 나타나져있습니다.
저 차트의 내용은 를 나타냅니다.
는 베이즈정리에 의해 이 되고,
은 이 되죠. 물론 우린 지금 몰라요.
은 Gaussian distribution의 pdf에서 오는 값이 됩니다.
이제는 parameter를 업데이트 해줘야 하는데, 빨간 가우시안의 경우
'나에게 속한 점들의 위치의 평균'으로 중심을 업데이트 하면 되겠죠.
근데, k-means에선 하나의 centroid에 속한 data instance가 분명했습니다.
근데 지금은 soft assignment잖아요?
중요한 점이 나옵니다!!!
여기서는 이제 각 data point가 Red에 속하는 그 확률 있잖아요?
이거요.
이거를 Red Gaussian Distribution은 가중치로 둬서 곱해줍니다.
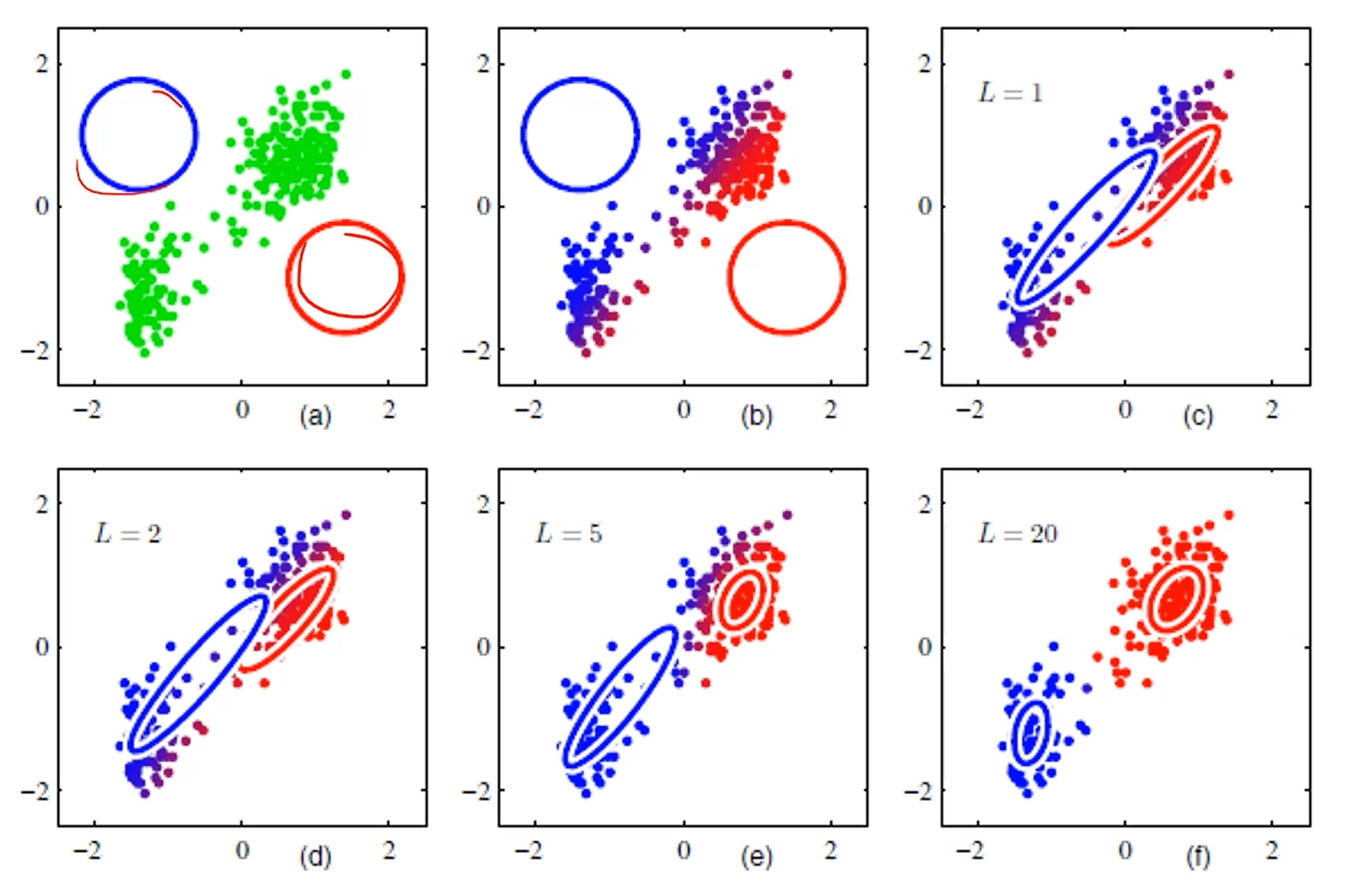
랜덤하게 distribution 두개를 할당해서,
파랑으로 분류될 경우와 빨강으로 분류될 경우를 각 data instance에 '확률'로 분배한다음,
그 내용을 가중치로 하여 각 gaussian distribution의 평균을 이동시킵니다.
Optimization of k-means clustering
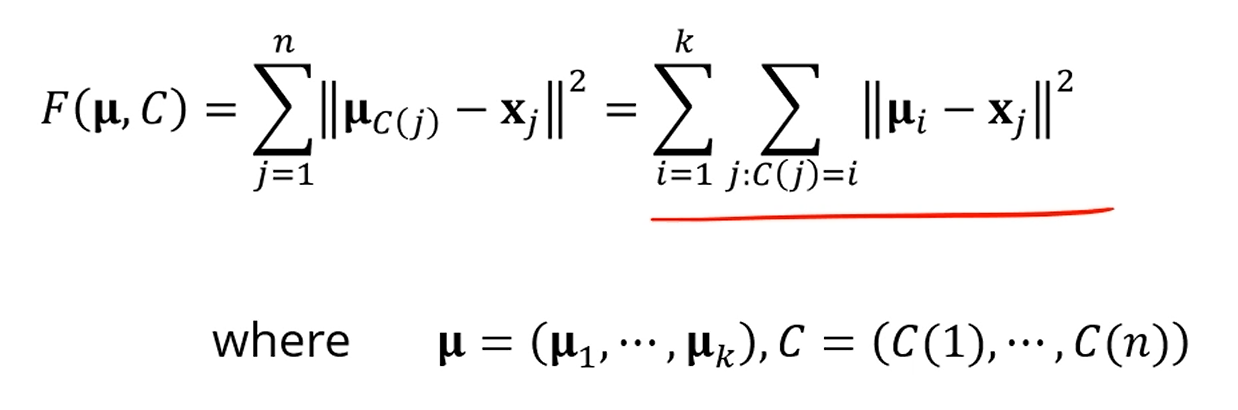
우리가 목표하는 바는 저 값을 최소화하는 와 를 찾는게 목표였구요.
어떤 class가 어떤 cluster에 속하는지 알려면,
cluster의 중심 알아야 합니다.
근데 cluster는 결국은 내부에 속한 instance를 알아야 cluster의 중심을 알 수 있습니다.
결국, cluster의 중심을 정하는게 먼저냐,
instance를 할당하는게 먼저냐를 정하는 문제에 부딪힙니다.
아까는 sample중 랜덤하게 centroid를 가정하고 업데이트를 했습니다.
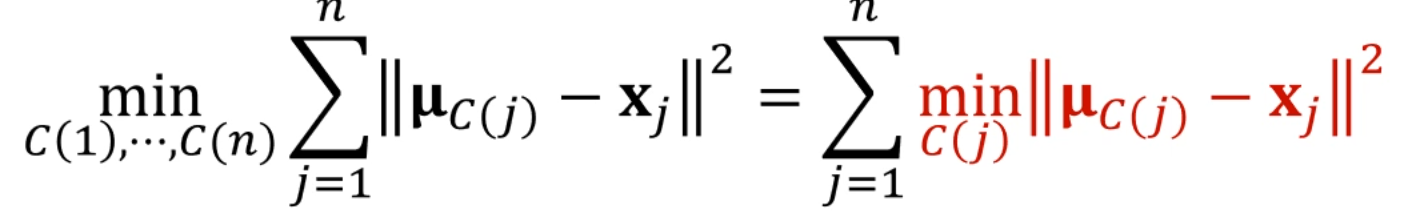
그래서 각 Class에 대한 를 고정하고, 이 오차들이 최소화되게끔 Class를 assign하는 것을
Expectation Step이라고 부르며,
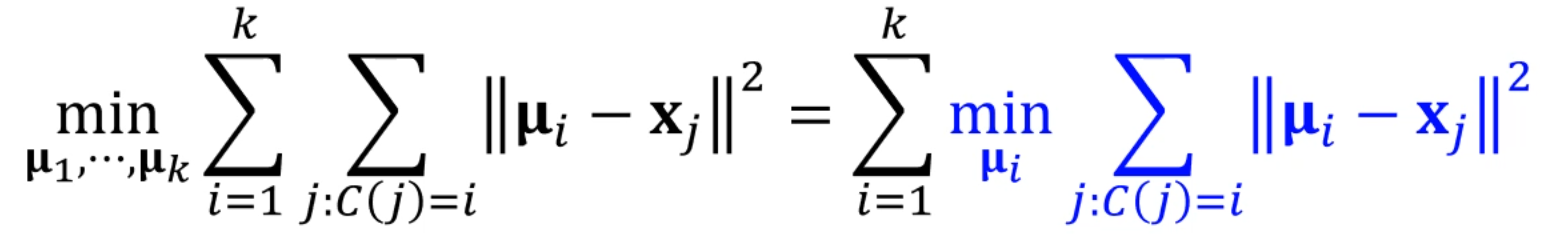
반대로 Class의 할당을 고정시킨 채로 를 업데이트 시키는 것을 Maximization Step이라고 부릅니다.
이게 EM입니다! Expectation, Maximization.
EMEMEMEMEMEM 반복하는거에요.
이 EM을 일반화를 해봅시다.
GMM에 적용해봅시다.
GMM의Expectation step에서는,
와 를 고정시켜놓고, C를 구하고, ()
Maximization step에서는
를 고정시켜놓고 와 를 업데이트하게 됩니다.
EM in GMM
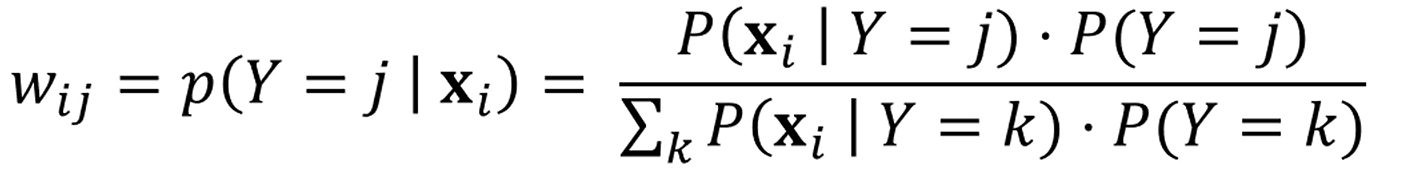
여기서는 를 구하게 되는데요,
이 확률은 가 에 속할 확률을 의미합니다.
앞서서는 분모 얘기는 안했는데, 이젠 분모도 계산해줍니다.
분자의 전체합으로 나누면 가 에 속할 확률이 계산이 됩니다.
그걸 전개해서 계산하면
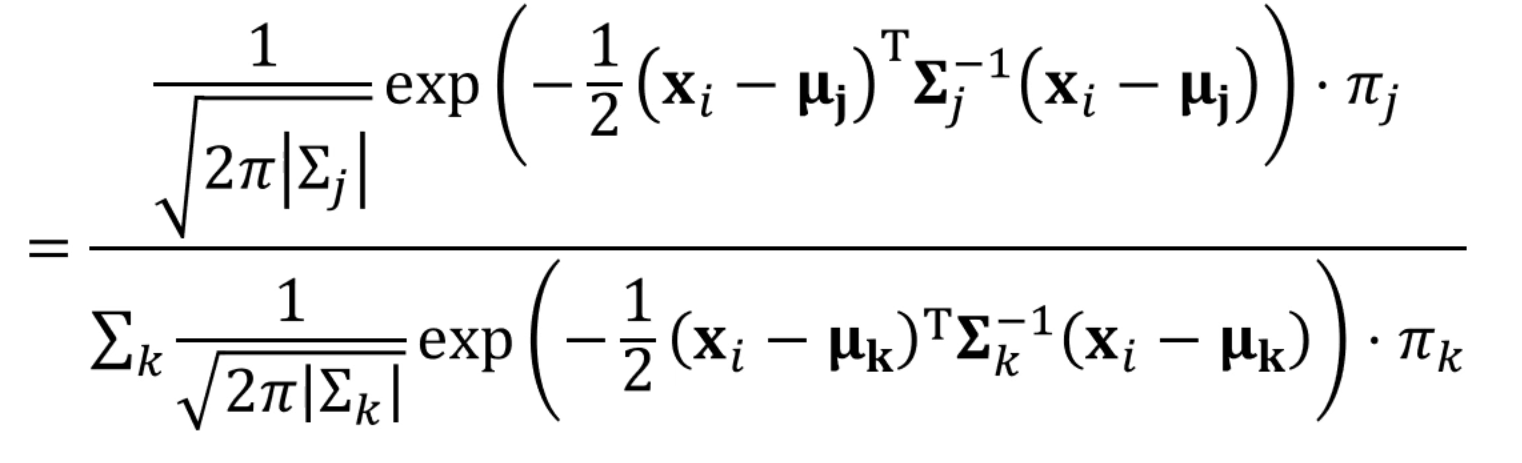
다음과 같이 나오는데요.
는 다 상수 꼴로 표현이 됩니다.
전항인 는 gaussian distribution을 따른다고 했으니,
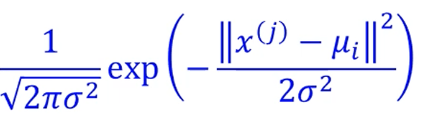
를 이용해주면 되겠죠.
= 임을 이용합니다.
결국, Expectation Step에서는
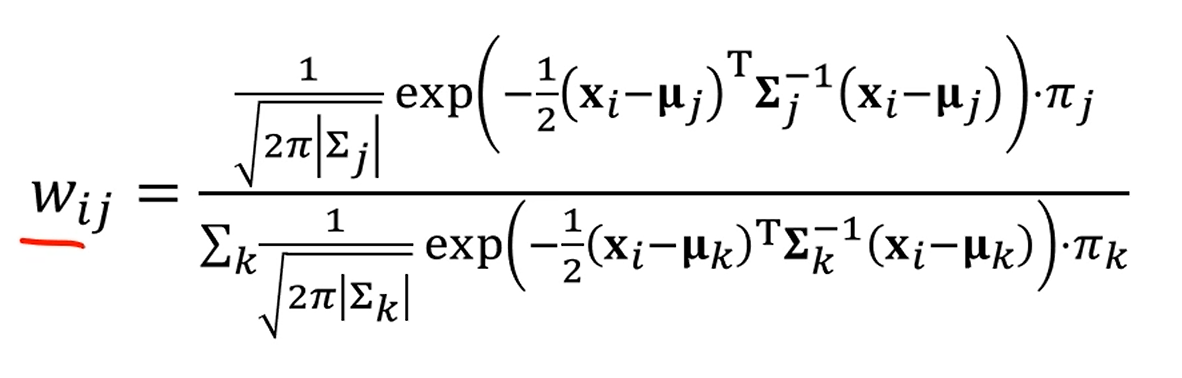
를 고정시키고 를 업데이트 해주고,
Maximization Step에서는
를 고정시키고 를 업데이트해주면 됩니다.
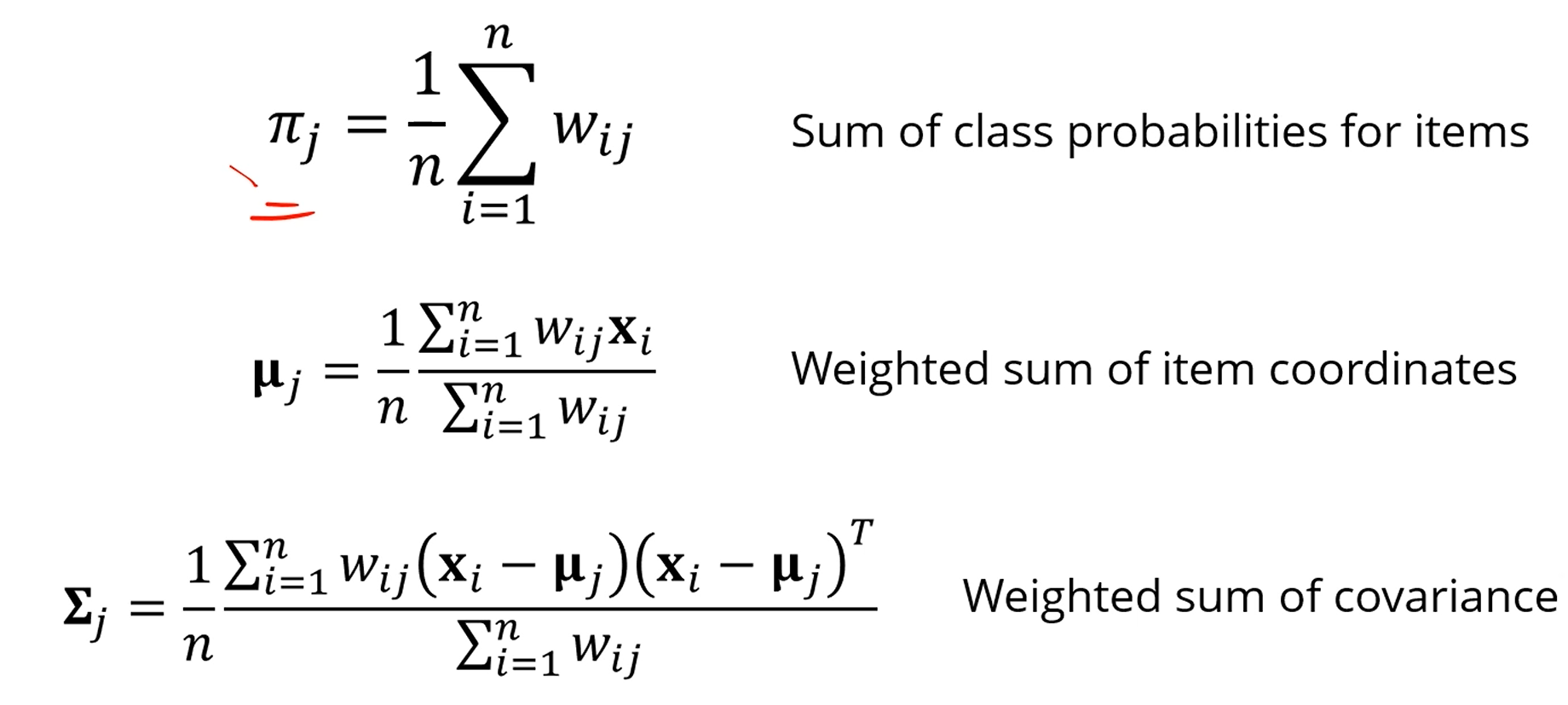
다음과 같이 업데이트가 가능합니다.
는 이 에 속할 확률, 가 에 속할 확률...을 다 더해주면 되겠죠.
거기에 평균을 취해준 것을 로 정의합니다.
는 모든 data instance 의 평균 위치를 구하는데,
이 때 가중치를 로 둡니다.
역시 가중치를 로 두면 됩니다.
How to generate Data from GMM?
그래서, GMM이 generative algorithm이라고 했는데,
어떻게GMM을 토대로 데이터를 생성할수 있을까요?
- 랜덤한 데이터를 각 의 확률을 토대로 생성합니다.
가령, = 0.7, , 이라면
해당 를 반영하여 instance를 생성합니다.
- R이 뽑혔다면, R에 해당하는 가우시안 분포에서 하나를 랜덤하게 샘플링합니다.
~
생성 완료!
Summary of GMM
k-means보다 flexible하고, 역시 빠르고
모든 parameter가 해석이 가능합니다.
해봤자 정도인데 전부 말하고자 하는 바가 명확하죠.
또한 Generative model입니다.
단점으로는 를 먼저 정해야 하고,
initialization에 민감합니다.
(그래서 k-Means를 먼저 조지고 그 친구의 결과값으로 initialize하기도 합니다.)
또, parameter가 차원의 제곱으로 늘어납니다.
d차원의 데이터가 주어지면, 는 d차원의 벡터지만,
는 차원의 행렬이죠.
