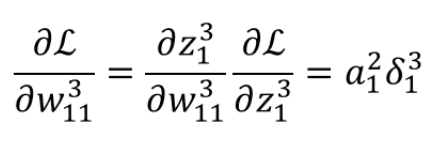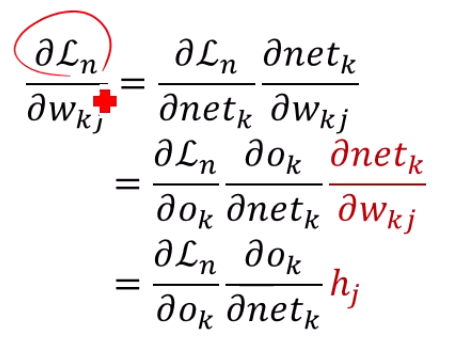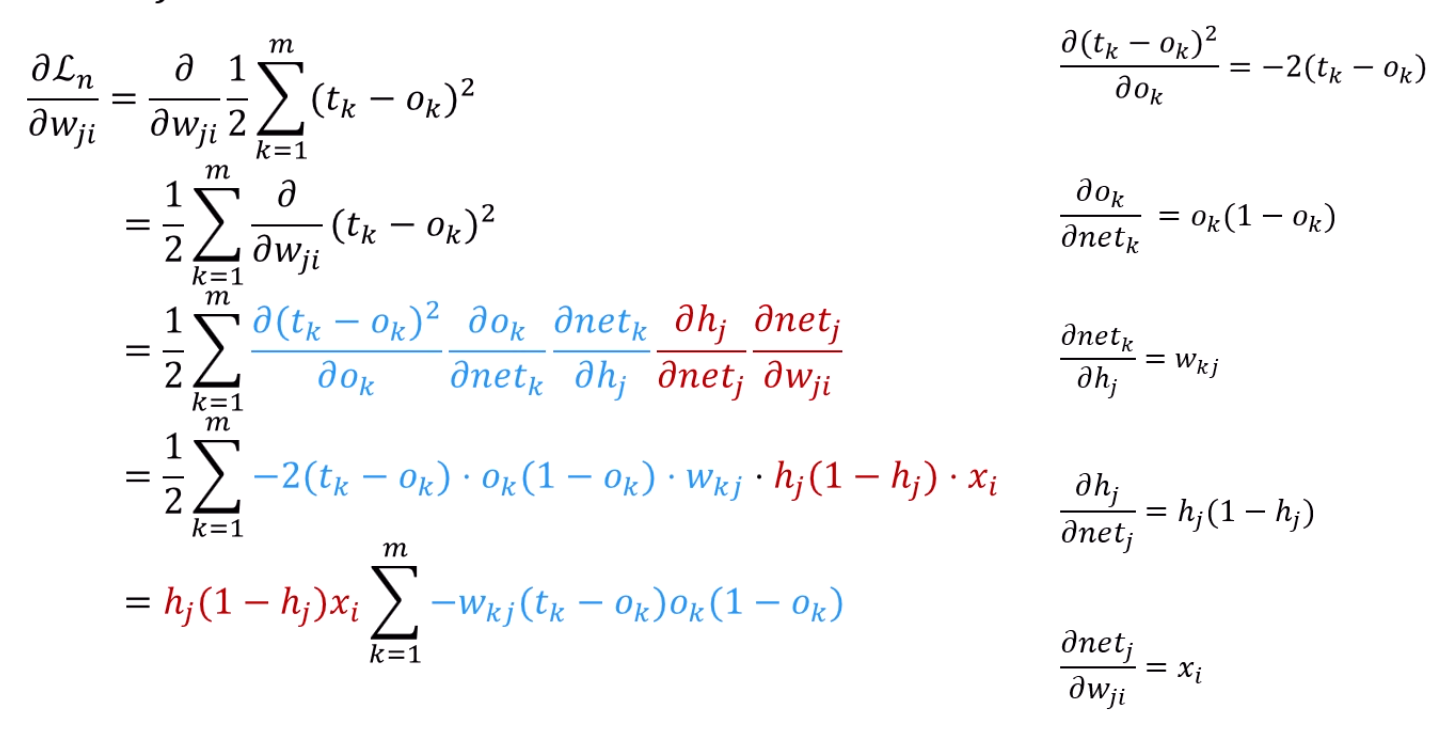Backpropagation

Backpropagation을 배울 때에는 기호에 압도되지 않으면 할 만 합니다.

알고 들어가면 좋을 것 중 두 개가 있습니다.

입니다.
또,

같이 computational graph를 그릴 때 하나의 변수가 두번 등장하는 경우,

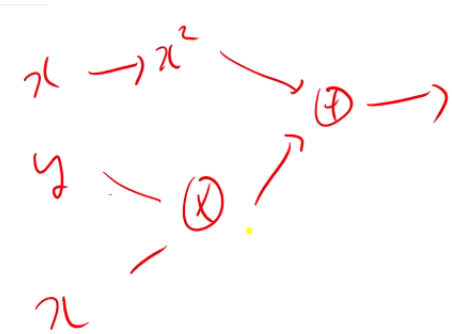
역전파를 통해 gradient를 계산하면
제일 위쪽 $x$가 받는 gradient는 2x입니다.
제일 아래 $x$가 받는 gradient는 y이구요.

이 경우에는, 그냥 $x$가 받는 gradient를 2x+y로 계산하면 됩니다.

Terminology

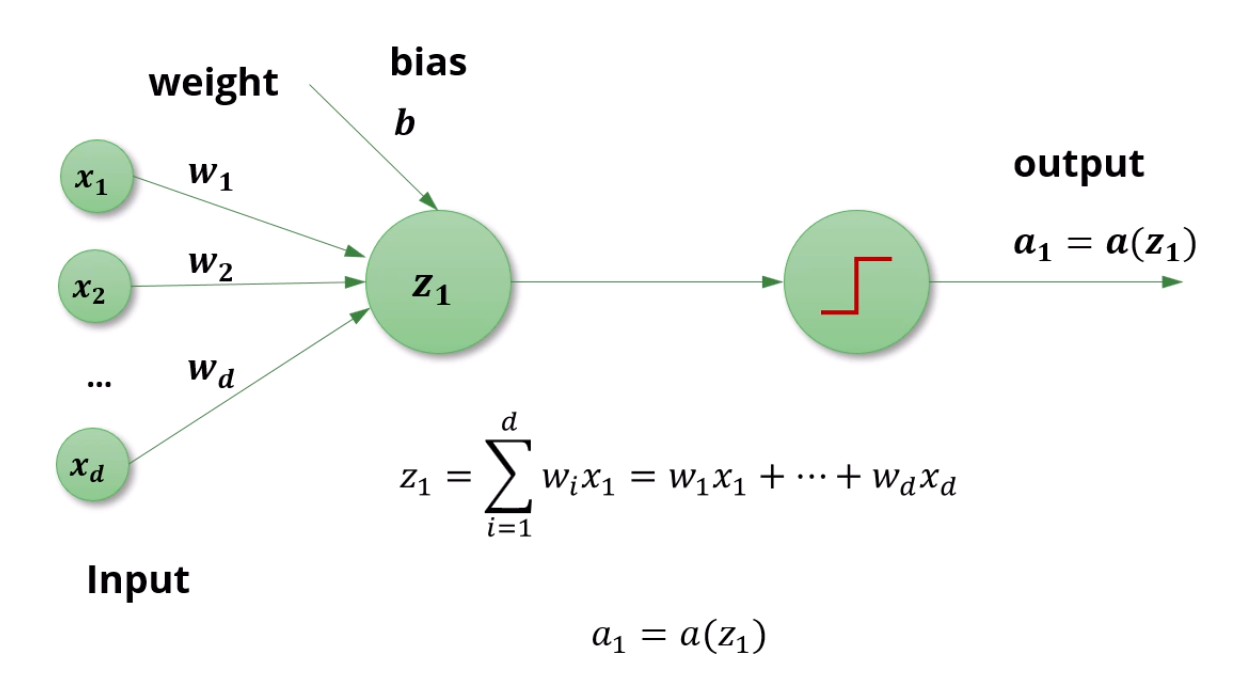
입력은 $x_1 ... x_d$로 표현합니다.
그 입력들에 대한 선형합은 $z_1 = \sum_{i=1}^dw_ix_i + b$로 표현합니다.

거기에 sigmoid까지 적용하면 $a$라고 칭합니다. $a_1 = a(z_1)$이 성립하겠죠.

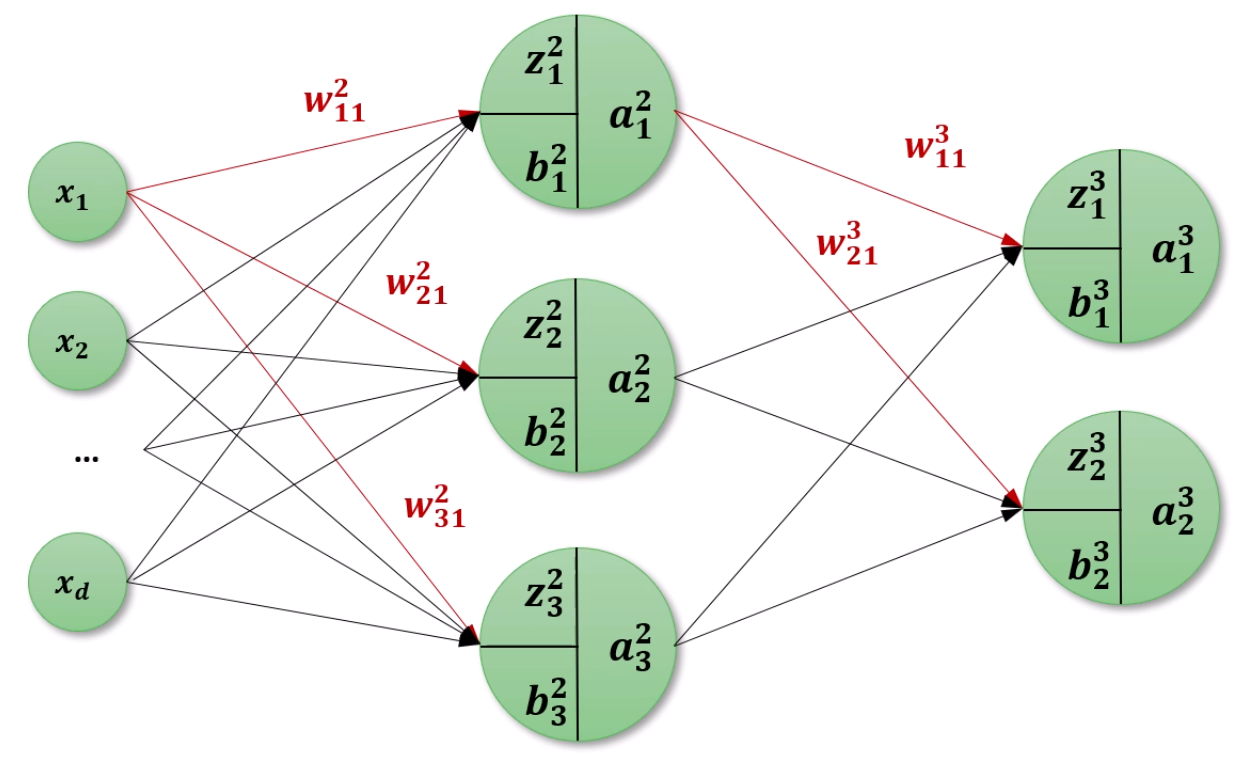
여러 node로 확장을 합니다.

하나의 neuron을 보면 3가지 값이 보이는데,
$z_1^2$는 2번째 layer의 1번째 node의 선형합이 됩니다.
$b_1^2$는 2번째 layer의 1번째 node의 Bias이구요.
$a_1^2$는 2번째 layer의 1번째 node의 Activation function까지 적용한 출력치입니다.

$w_{11}^2$는 $node_1^2$로 향하는 이전 layer의 1번째 node에서 온 weight다
이렇게 이해하면 되겠습니다.

$w_{13}^2$는 $node_1^2$로 향하는 이전 layer의 3번째 node에서 온 weight다, 이렇게 되겠구요.

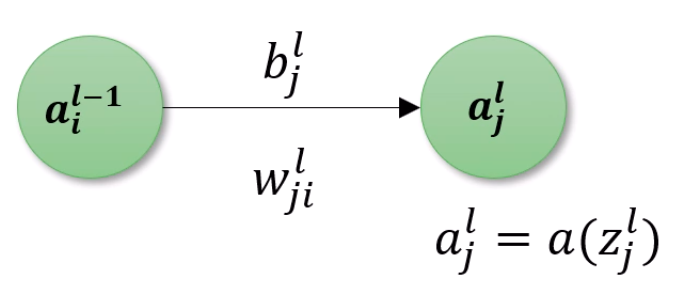
이것만 이해하면 Terminology는 어렵지 않습니다.

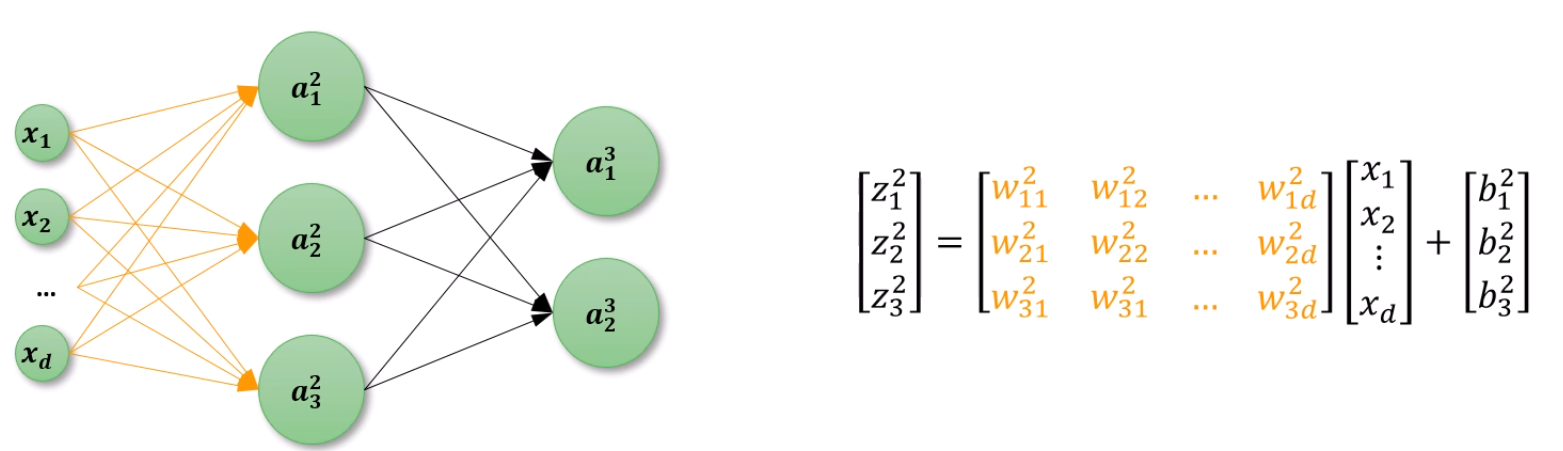
Forward Computation을 할 때 Matrix Representation으로도 나타낼 수 있습니다.
2번째 layer의 선형합 결과인 $z^2_1$은 $w_{21}^2, w_{22}^2, ...$와 각 입력 layer들의 선형합에 bias를 더한것으로 표현되죠.

마지막으로 나온 출력층의 결과와 정답의 결과를 비교하여,
Loss Function을 정의할 수 있습니다.

지금은 그냥 MSE로 정의한 것 같네요.
Cross-Entropy같은 방식으로 정의할 수도 있습니다.

만약 $\mathcal{L}_i(w) = \frac{1}{2}\sum_{k=1}^m(o_{ik}-t_{ik})^2$,
$\mathcal{L}(w) = \sum_{i=1}^n \mathcal{L}_i(w)$로 정의한다면,

이 $\mathcal{L}$을 학습가능한 모든 가중치로 미분합니다.
가령 $\frac{\partial \mathcal{L}}{\partial w_{11}^2}$를 구한다면, 그건 다른 표현으로 $\Delta w_{11}^2$가 되고,
그 값에 learning rate $\eta$를 곱해서 가중치를 업데이트 해주겠죠.

물론 layer가 커질수록 이 과정이 엄청 복잡해지는데,
(식이 많이 쌓이기 때문이에요)
이걸 Computational Graph로 극복할 수 있습니다.

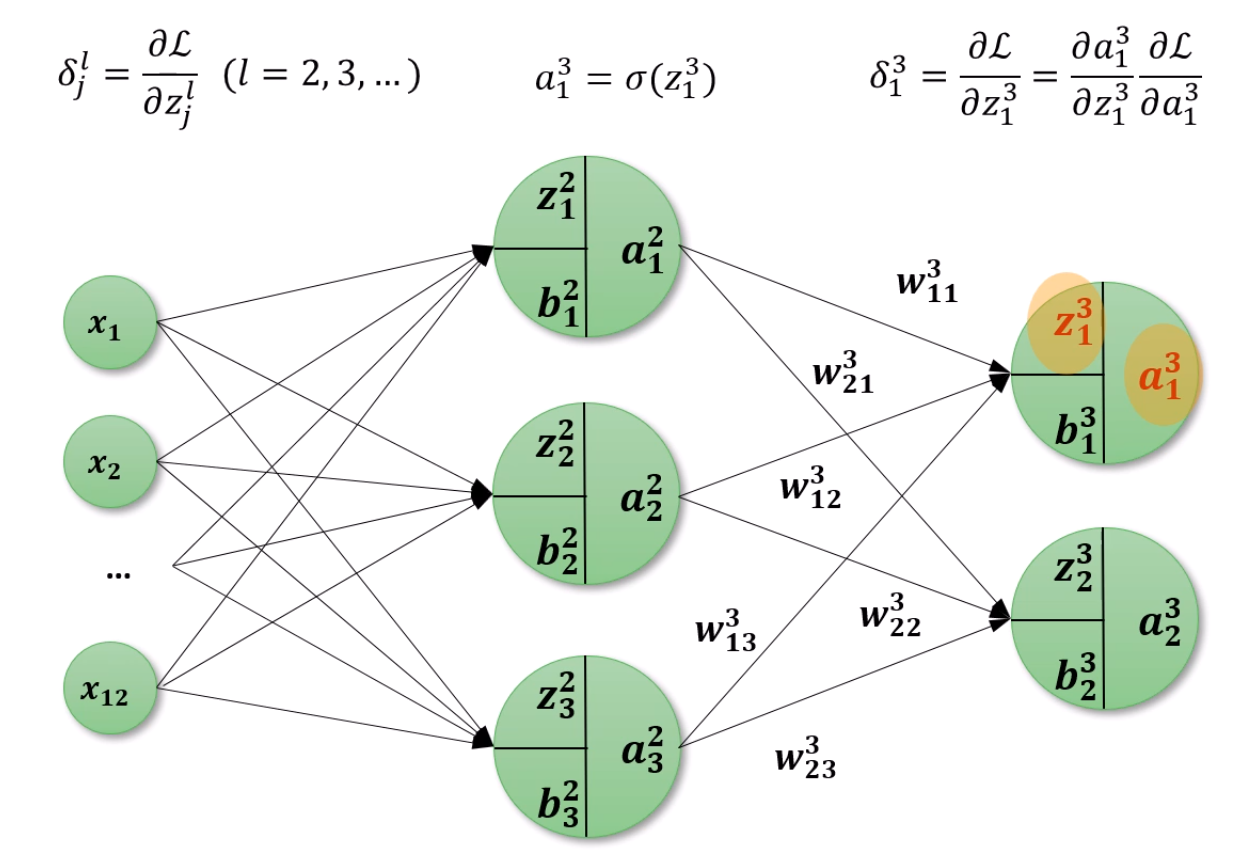
다음과 같은 식에서, 우리가 궁극적으로 찾고자 하는 건,
$w...$와 $b...$들의 기울기를 계산하는게 목표입니다.
$\frac{\partial \mathcal{L}}{\partial w...}$와 $\frac{\partial \mathcal{L}}{\partial b...}$를 다 찾는게 목표인거죠.

$b$와 $w$에 대한 미분값을 알기 위해서는 자연스럽게
$z$와 $a$도 전부 기용하게 됩니다.

우리가 아는건, $z$가 앞쪽 layer의 수많은 $a$들과 자신으로 향하는 수많은 $w$의 선형합, 거기에 bias까지 더해서 만들어진 것을 알고 있습니다.

$z^3_1 =$ 선형합 + $b_1^3$이죠?
그러면 gradient를 역 분배 해줄 때,

$x+y=k$면, $k$의 gradient가 5일 때, Backward propagation에서
$x$와 $y$에 gradient가 얼마씩 들어갔죠? 5씩 들어갔습니다!

따라서 $\frac{\partial \mathcal{L}}{\partial z_{1}^3}$ = $\frac{\partial \mathcal{L}}{\partial b_{1}^3}$이 되는거죠.

$w_{13}^3$ 입장에서 볼까요?
$z_1^3$은 선형합 + 선형합 + $w^3_{13}a^2_3$입니다.
gradient를 분배해주면, 결국
$\frac{\partial \mathcal{L}}{\partial w_{13}^3} = \frac{\partial \mathcal{L}}{\partial z_{1}^3} \times\frac{\partial \mathcal{z^3_1}}{\partial w_{13}^3}$이 되는데,
앞의 gradient는 알고 있고, 뒤의 gradient는 결국 $a_3^2$와 같죠.

결국 포인트는, $\frac{\partial \mathcal{L}}{\partial z_{j}^l}$만 알면 나머지 bias나 weight는 너무 쉽게 구해진다는 것입니다.
선형합이거든요.

그리고 그 매우 중요한 $\frac{\partial \mathcal{L}}{\partial z_{j}^l}$를, 특별한 이름으로 $\delta_j^l$로 부르겠습니다.

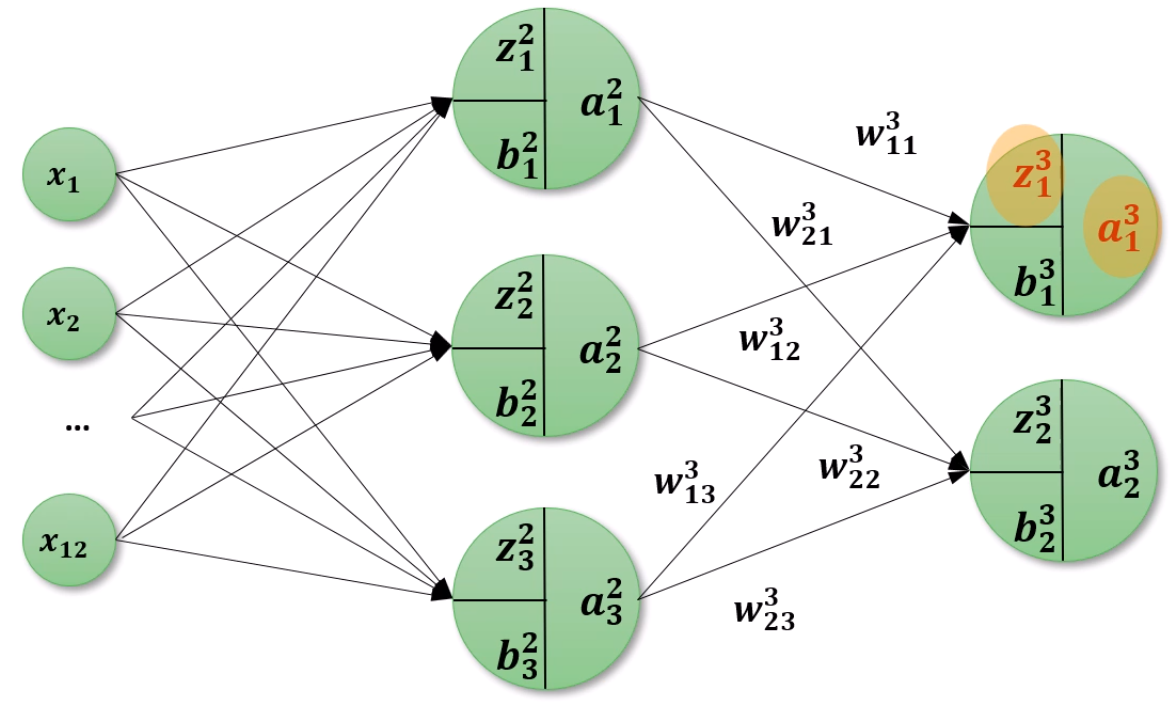
$a_1^3$은 $\sigma(z^3_1)$이고,
우리가 구하고 싶은 $\delta_1^3$은 $\frac{\partial \mathcal{L}}{\partial z_{1}^3}$이고, 그 값은 $\frac{\partial \mathcal{L}}{\partial a_{1}^3}\frac{\partial a_1^3}{\partial z_{1}^3}$과 같습니다.

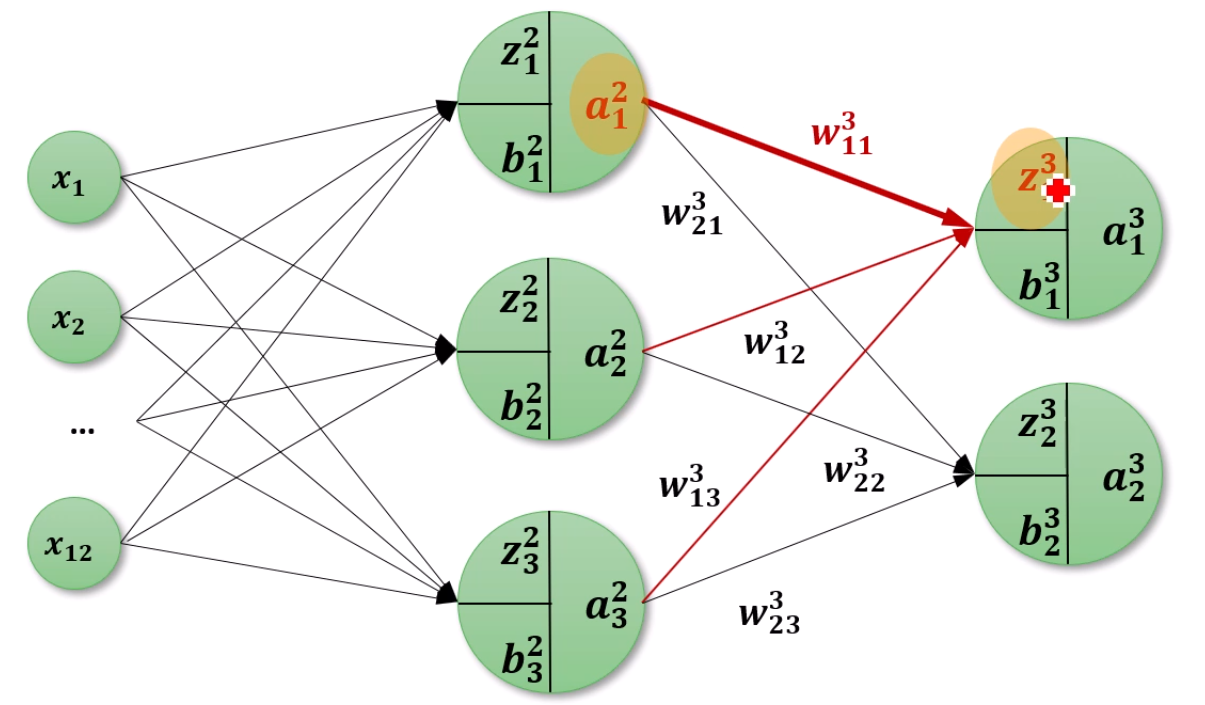
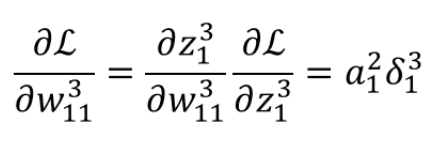
이제 Weight에 대한 gradient를 구할 수 있습니다.
앞서 아는 내용이 $\frac{\partial \mathcal{L}}{\partial z_1^3}$이었으니, 그 값을 이용해 Chain Rule을 적용하면
앞의 중요한 $\delta$와 $a_1^2$와의 곱으로 나타난다~를 알 수 있습니다.

또 강조됐죠. 결국은 $\delta_j^l$이 중요합니다.

이 내용이죠.

weight는 구했는데, 그럼 bias의 미분값은요?

더 쉽죠.
$z =$선형합 + $b$ 잖아요?
$\frac{\partial \mathcal{L}}{\partial z}$의 값 ($\delta$)가 그대로 분배됩니다.

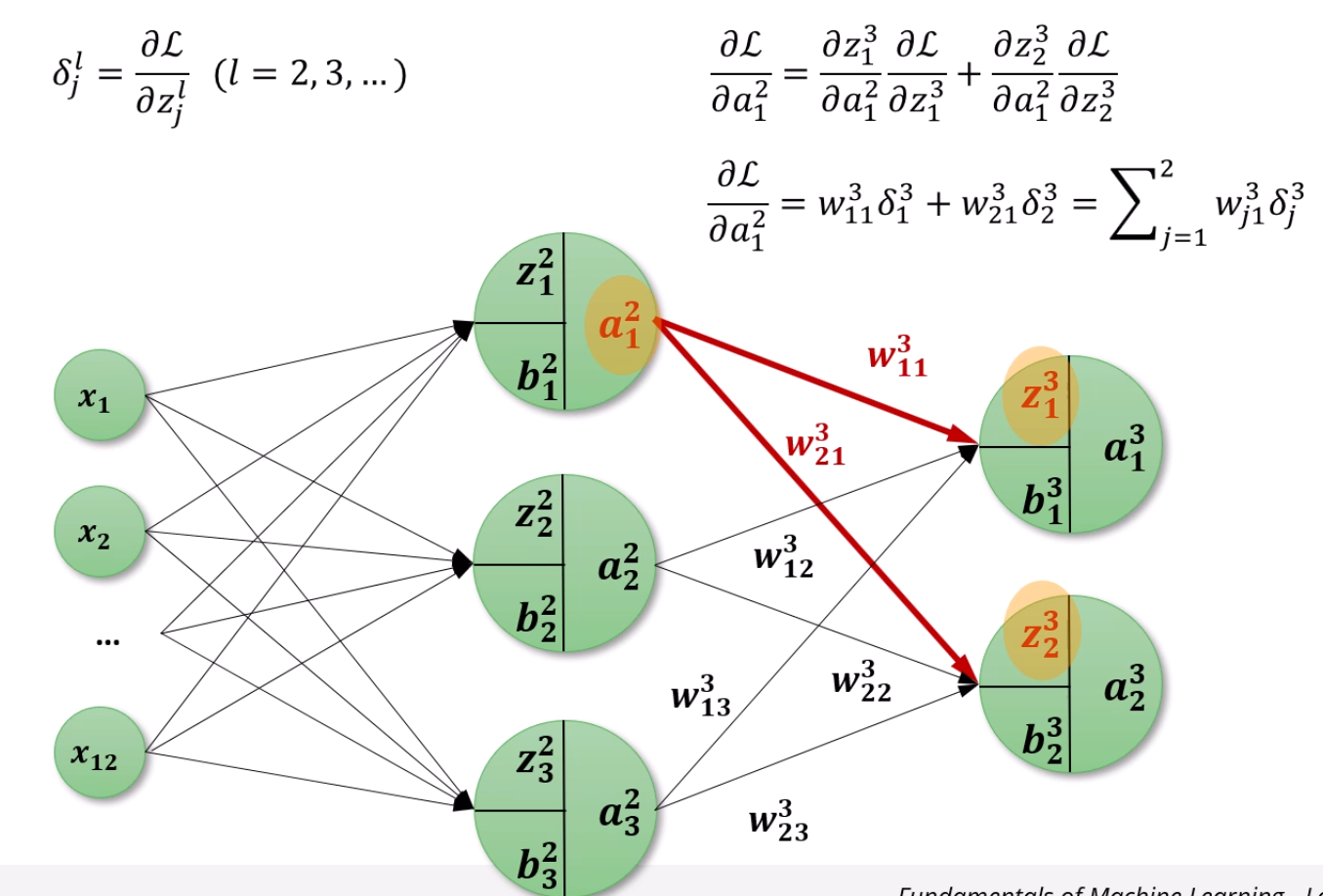
자, 이제는 $a$에 대한 gradient를 구해봅시다.
여기서 보이듯, $a_1^2$는 총 2개의 $z$에 영향을 미치고 있습니다.
backward로 계산되는 gradient도 2개가 오겠죠?

선형합 + $a_1^2w_{21}^3 = z_2^3$이고, 선형합 + $a_1^2w_{11}^3 = z_1^3$입니다.

결국 $a_1^2$가 감당할 gradient는 $\delta_2^3w_{21}^3 +\delta_1^3w_{11}^3$이 되겠네요.

굳이 $\sum$으로 표현하면 $\sum_{j=1}^2w_{j1}^3\delta_j^3$으로 표현됩니다.

아 또 나왔죠. 결국은 $\delta$가 또 또 중요합니다.

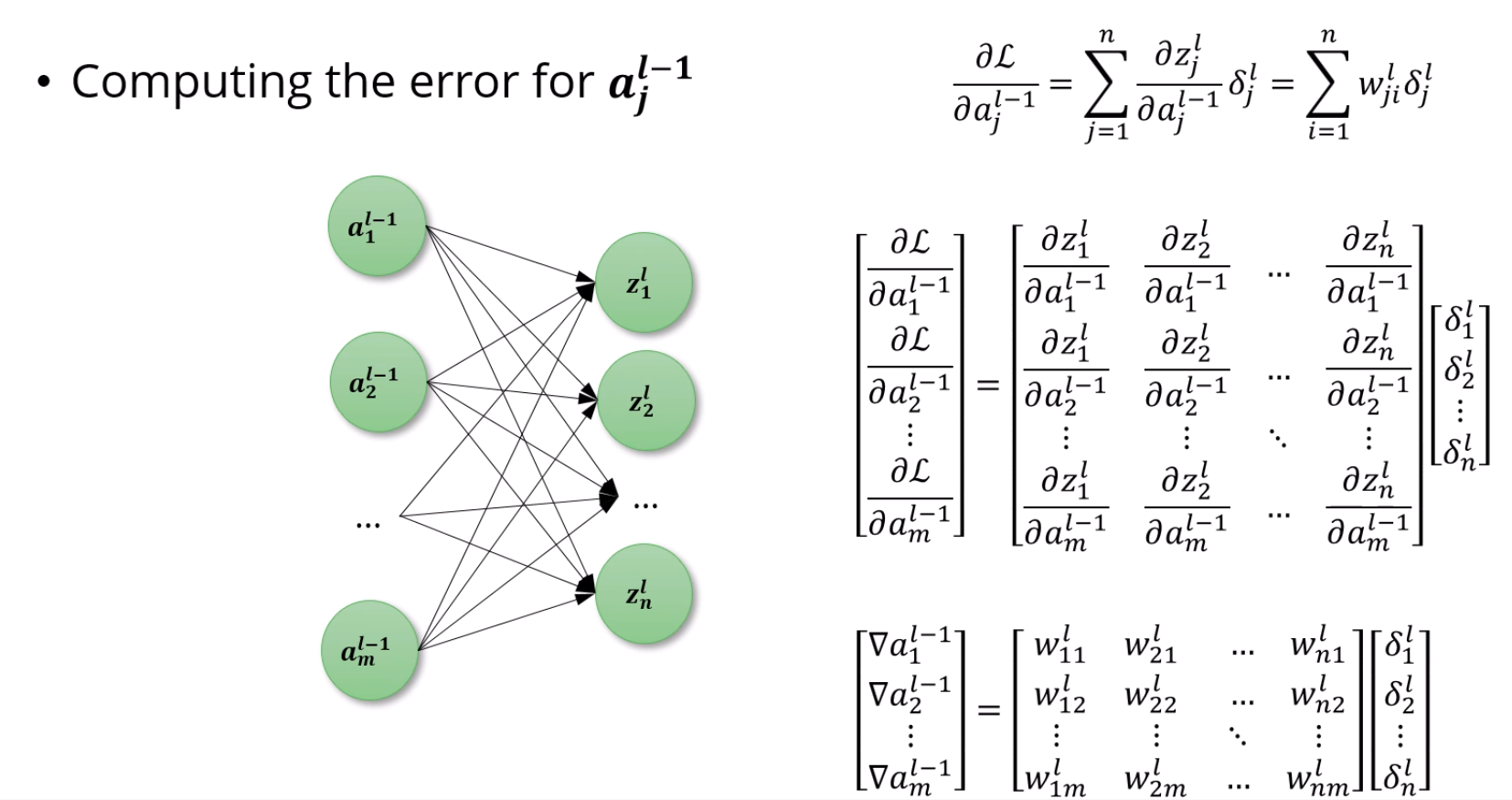
무한히 복잡해보이는데, 그냥 matrix representation으로 일반화를 했을 뿐입니다.
그냥 $a$의 gradient는 ($\nabla a$) $z$에 대한 $a$의 gradient $\times$ $L$에 대한 $z$의 gradient ($\delta$)의 합으로 표현된다,
근데 $z$에 대한 $a$의 gradient가 해당 $z$로 향하는 $w$니까,
$w_{11}^l \times \delta_1^l + w_{21}^l \times \delta_2^l + ...$ = $\nabla a_1^{l-1}$이라고 생각하면 되겠습니다.

어렵진 않아요!

조금 더 simple한 예시를 봅시다.

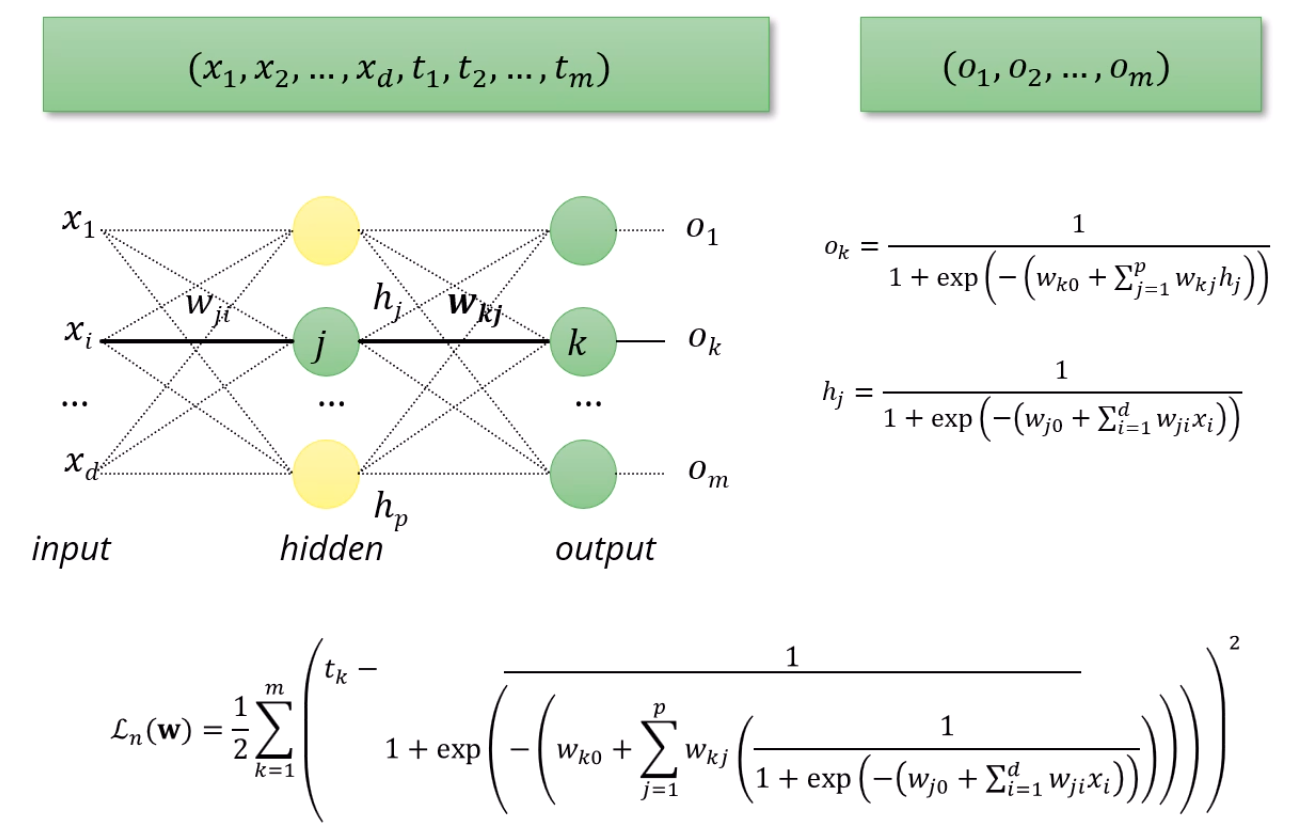
hidden층 딱 하나, 출력층 딱 하나로 구성되어 있다고 합시다.
원래 $w_{ji}^k$로 표시되던건 k번째 layer의 j번째 node로 향하던 i번째 node로부터의 weight인데,
이젠 그런 몇번째 layer를 구분할 필요가 없으니,
$w_{ji}^k$는 $w_{ji}$로 단순화됩니다.

$h_j$는 hidden의 j번째 node의 output인데요,
sigmoid인 $\frac{1}{1+e^{-x}}$를 activation function 삼아서,
거기에 input으로 $w_{j0} + w_{j1}x_1 + w_{j2}x_2 + ... + w_{jd}x_d$를 넣어준 것이죠.

$o_k$는 output의 k번째 node의 output이고,
sigmoid를 activation function으로 삼아서,
그 input으로 $w_{k0} + w_{k1}h_1 + w_{k2}h_2 + .. + w_{kp}h_p$를 넣은거구요.

그리고 그걸 쭉~~ 써서, Loss를 MSE 방식으로 표현한게 밑의 $\mathcal{L}_n(w)$ 식입니다.

쉽죠?
식에 압도당할 필요는 없습니다.

근데 아무튼 우리는 Loss Function을 미분...을..해야하는데
솔직히 저 복잡한 식을 미분하고 싶지는 않잖아요?
Chain Rule을 사용할 수 있습니다.

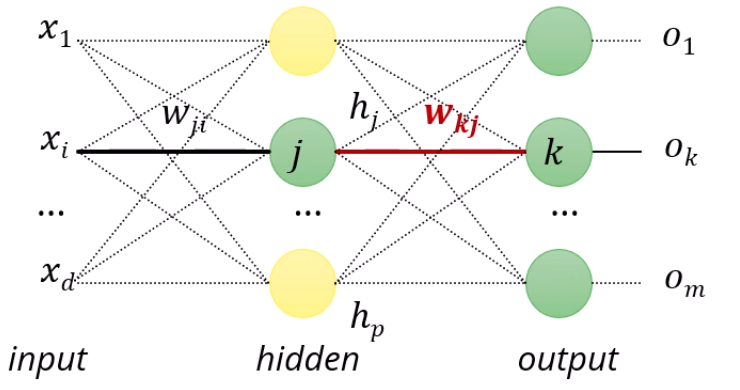
$w_{kj}$의 gradient를 구해봅시다.
$w_{k1}h_1 + w_{k2}h_2 + .... + w_{kp}h_p = net_k$로 정의합니다.
$net_k$는 $k$ node가 받는 입력값이 되겠죠.

그러면 $o_k$는 $sigmoid(o_k)$가 되구요,
$\mathcal{L}_n(w) = \frac{1}{2}\sum_{k=1}^m(t_k-o_k)^2$로 정의합니다.

한번만 back propagation을 해봅시다.

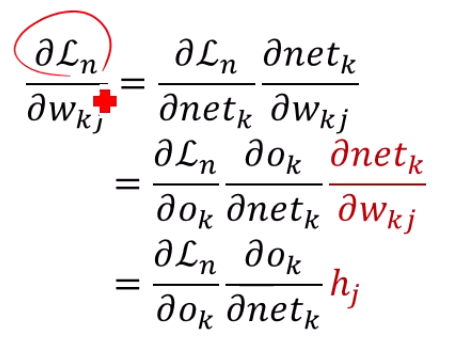
$net_k$를 $w_{kj}$로 미분하면 붙어있는 $h_j$만 튀어나오겠죠.
앞에 붙은 gradient들은요?

$\frac{\partial \mathcal{L}}{\partial o_k}$는 loss function을 output으로 미분하는 것이니까,
평범한 합성함수 미분과 같죠. $-(t_k - o_k)$가 나옵니다.

$\frac{\partial {o_k}}{\partial net_k}$는 $o_k = sigmoid(net_k)$임을 이용하면, sigmoid 함수 미분이 됩니다.
앞에서 했었죠!

이 값은 $sigmoid(net_k)(1-sigmoid(net_k))$이며, $sigmoid(net_k) = o_k$니까,
$o_k(1-o_k)$가 되겠네요.

결국 구하고자 하는 $\frac{\partial \mathcal{L}_n}{\partial w_{kj}} = -(t_k-o_k)o_k(1-o_k)h_j$가 됩니다!

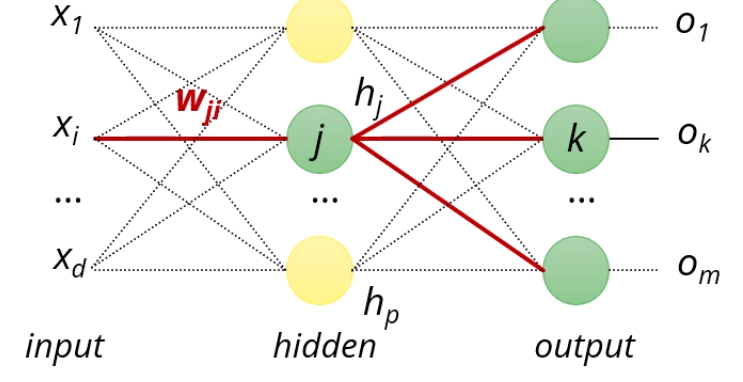
input과 hidden 사이의 $w_{ji}$의 gradient를 구하려고 해도, 똑같습니다.
Chain rule만 조금 추가될 뿐입니다.

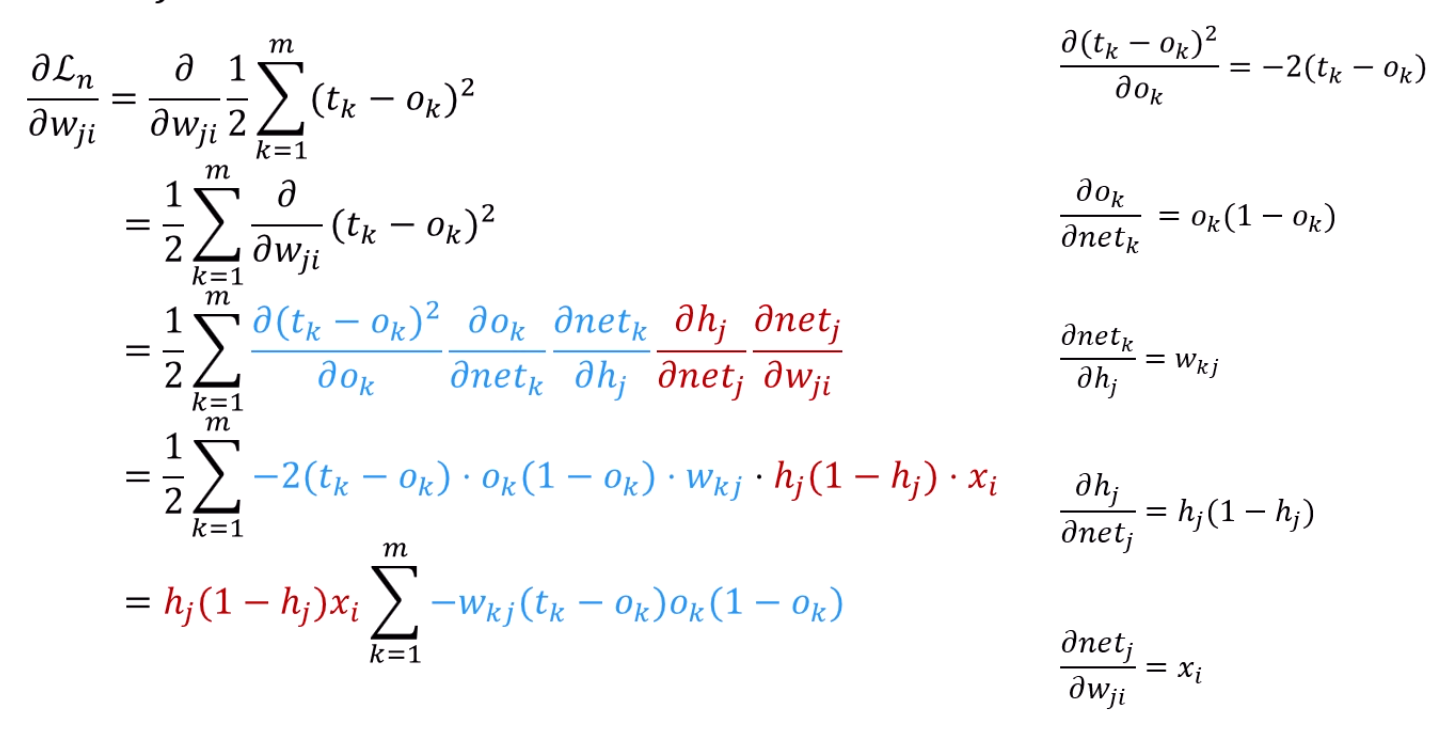
차근차근히 직접 해보면, 어렵지 않아요.

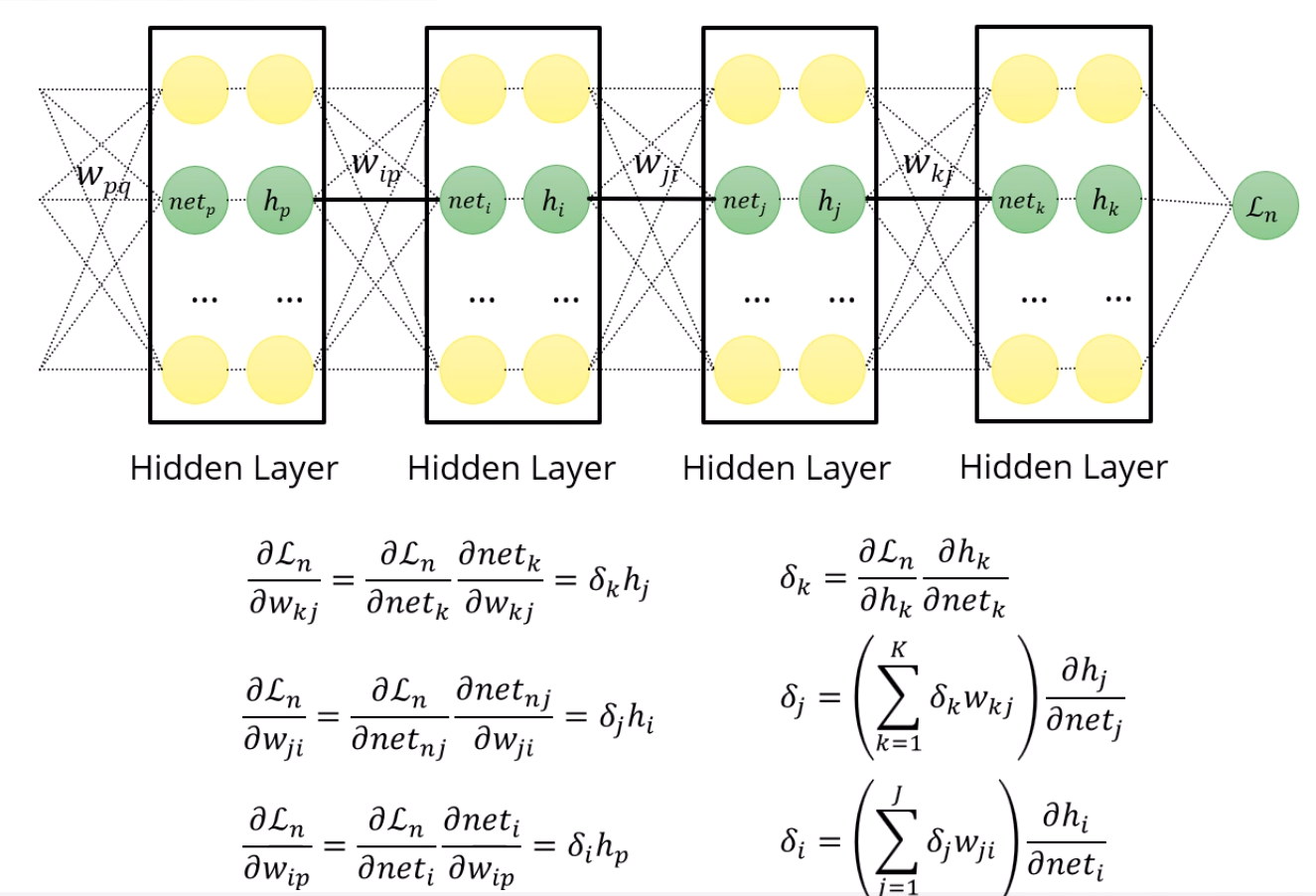
무식하게 식을 다 외우는 것보다는,
결국은 Loss를 $h_k$에 대해 미분하고,
$h_k = \sigma(net_k)$임을 이용해서 $net_k$의 gradient도 구하고,
$net_k$의 gradient를 이용해서 $w$들의 gradient도 구하고,
그 $w$들의 gradient를 이용해서 $h$들의 gradient도 구하고,
그걸 다시 이용하고,,,

그냥 이걸 해주면 됩니다.