전체 데이터는 엄청나게 고차원 공간에서 무작위하게 분포합니다.
하지만 실제 데이터는 나름, 고차원에서 나름의 패턴을 잡고 분포합니다.
그래서, 실제로 필요한 dimension은 갖고 있는 수많은 dimension 보다 좀 적지 않을까.
이런 가설이 존재합니다.
물론, numpy로 random vector를 만드는 등의 uniform한 데이터들은
패턴같은게 존재하지 않습니다. ML도, 시각화도 불가능하죠.
하지만 다행히도 현실에 존재하는 데이터는 밀도가 불균일하며,
그 중에서도 특정 영역에만 높게 밀도가 분포합니다. (다행이네요!)
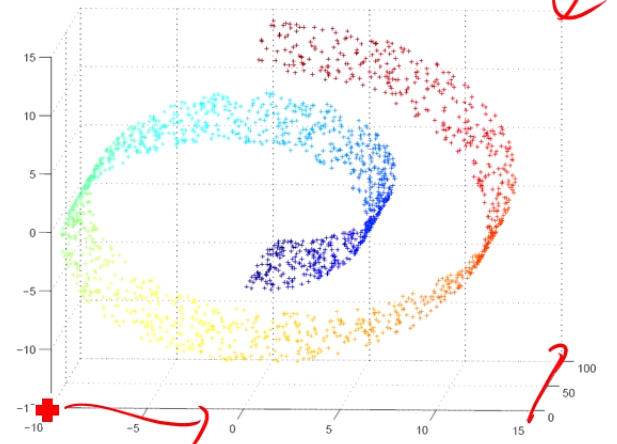
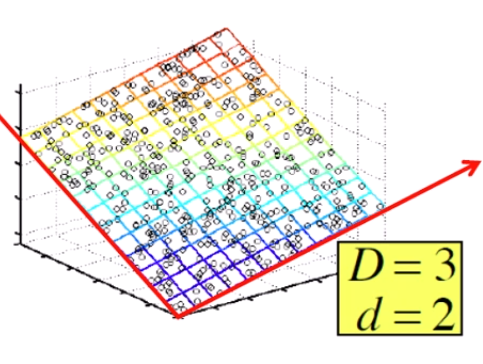
약간 이런 느낌입니다.
축은 3개인데, 축 3개를 다 쓰는게 아니라, 데이터가 실제로는
2개의 축을 써서 분포되게끔 그려져 있는 거죠.
이런 식으로,
실제 데이터는 초 고차원이지만, 그건 저차원의 몇 개의 dimension만으로 표현이 가능할 것이다,
이런 가설을 Manifold Hypothesis라고 부릅니다. (했었죠?)
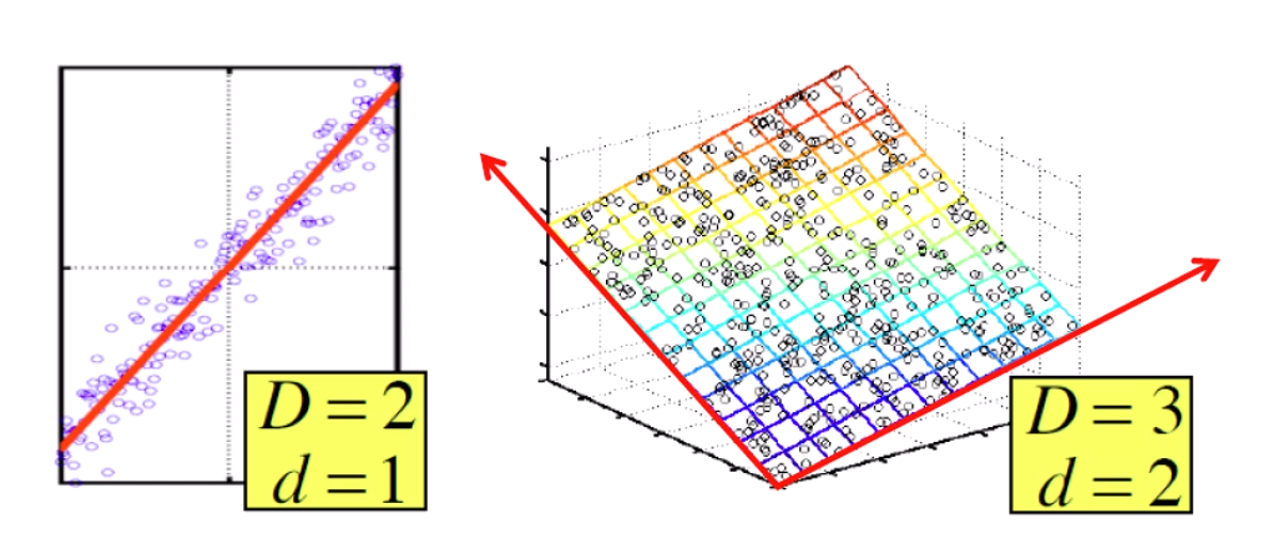
이렇게 차원이 높은 데이터를 가지고 있을 때,
그걸 잘 표현하는 저차원의 데이터를 찾는 것을 Dimensionality Reduction이라 부릅니다.
좌측 그림에선, 2차원 평면 위에 분포한 이 점들을
빨간 선을 긋고, data point를 수선의 발을 그려 1차원으로 내릴 수 있겠죠?
우측 그림에선 3차원 공간에 분포한 데이터를 2차원 평면을 만들어서
평면에 내릴 수 있겠죠.
다음과 같이 5차원 데이터도 2차원 데이터로 잘 특성만 따온다면, 내리기가 쉽습니다.
을 k차원으로 줄여봅시다.
먼저 생각할 수 있는 것은 선형합입니다.
...
물론, 저 가중치 nk개는 우리가 직접 구하긴 해야죠.
이렇게 선형합을 이용해 차원축소 하는 Linear Dimensionality Reduction 알고리즘에는
PCA, NMF, LDA가 있고,
예시로 PCA를 배워볼 것입니다.
비선형적인 차원축소도 존재합니다.
Isomap, LLE, t-SNE가 있습니다.
예시로 t-SNE를 배워볼 것입니다.
Why dimensionality reduction?
차원을 줄이면, 데이터 간에 숨어져 있는 상관관계도 보이고,
중복된 feature도 제거가 됩니다.
데이터 저장 / 처리도 쉬워지구요,
무엇보다 표현하고 해석하기 좋아집니다.
Rank of a matrix
Matrix A의 rank를 구하려면,
matrix A의 column 중 몇 개가 linearly independent한지 보면 됩니다.
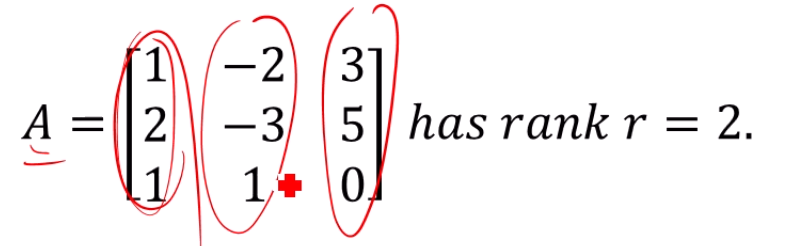
(1,2,1)과 (-2,-3,1)은 linearly independent한데,
(3,5,0)은 (1,2,1) - (-2,-3,1)이니까, linearly dependent하죠.
2개만 서로 독립적이네요. rank는 2입니다.
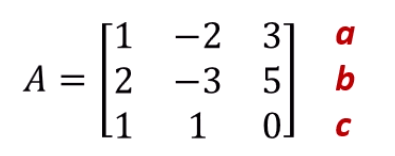
이런 경우에, 우린 원래 행렬을 좀 더 이쁘게 기술이 가능합니다.
rank가 3이 아니니까,
[1,2,1]을 하나의 축으로, [-2,-3,1]을 하나의 축으로 보면,
[3,5,0]은 두 축이 span하는 공간 위의 어느 vector가 됩니다.
3차원인줄 알았는데, 그 3차원을 기술하는 데 벡터가 2개만 필요하니까
새로운 축 2개를 잡아서 축소를 한다!
이렇게 생각하면 됩니다.
Linear Independence
full rank인지 아닌지 확인하려면, linear independence를 보면 됩니다.
이렇게 determinent를 구하면, det(A) = 0일 때 linearly dependent한 벡터가 존재하게 됩니다.
지금은 det(A) = 5니까, linearly independent하고 rank는 2겠네요.
Orthogonal
벡터 공간에서 축은 직교해야 합니다.
<x,y> = 0이라는 건 와 가 직교한다는 것을 의미합니다.
또한, 둘이 orthogonal하면서 unit vector라면 orthonormal하다고 합니다.
Eigenvalue, Eigenvector
가 성립한다면, 그 때 를 A에 대한 Eigenvalue, 를 A에 대한 Eigenvector라고 부릅니다.

이미지의 축이 틀어졌는데, ()
벡터의 방향이 바뀌지 않았으니 파란 벡터는 Eigenvector이며,
심지어 크기도 안 바뀌었으니 Eigenvalue는 1입니다.
즉, 가 성립하는거죠. (파란 벡터에 대해서요)
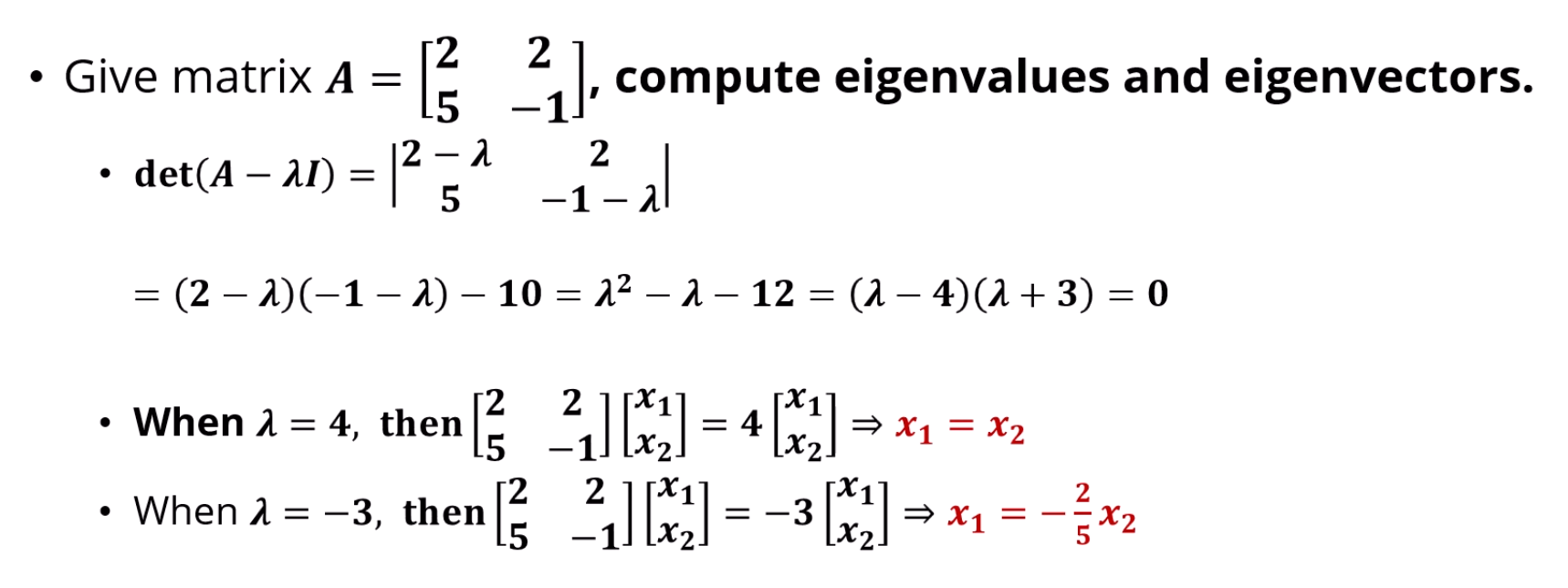
Eigenvalue, Eigenvector 구하는 방법입니다.
에 대해 determinent를 구하면 eigenvalue가 나옵니다.
eigenvalue를 넣고 를 풀어주면 v가 나옵니다.
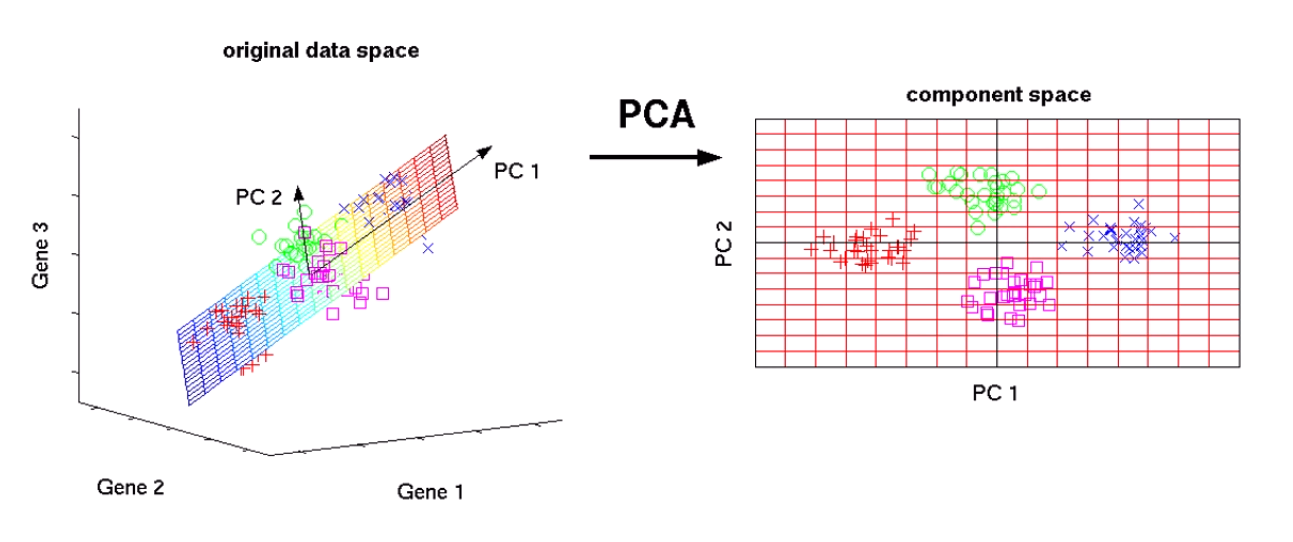
PCA (Principal Component Analysis)
어떤 고차원 데이터가 주어졌을 때, 고차원 데이터를 기술하는 다른 좌표축을
찾아내는 알고리즘입니다.
원래 3차원이라고 하면, x,y,z차원을 잘 선형조합 해서
새로운 3개의 차원을 찾아냅니다.
근데, PCA로 찾은 새 차원은 순서가 있습니다.
PCA1차원으로 향하면, 원래 데이터의 분산이 최대가 됩니다.
그것과 orthogonal한 PCA2차원으로 향하면, 그 다음으로 분산이 최대가 되는 방향이 됩니다.
n차원에서 PCA를 하면 n개의 축이 나오는데,
그 중에서 우리가 k개를 뽑아 쓰는겁니다.
좀 high-level하게 생각하면,
막 떠다니는 수많은 데이터들을 보고,
이런저런 방향에서 살펴보다가, 데이터가 가장 퍼지게 보이는 그 시점에서
캡처를 찰칵 합니다.
그 캡처본이 PCA의 결과라고 생각하면 됩니다.
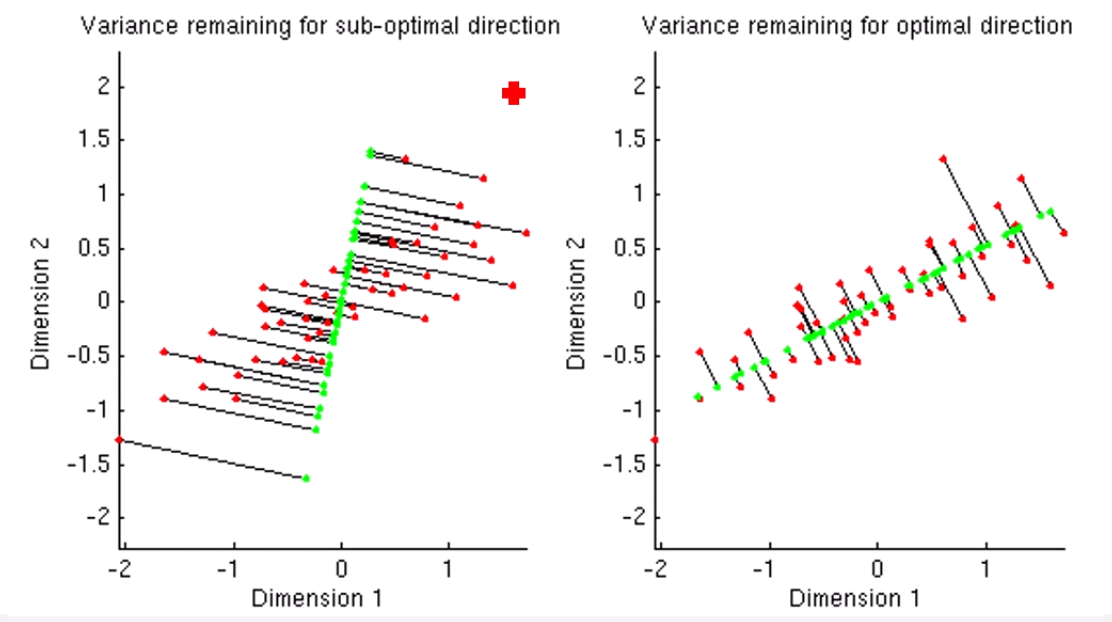
2차원을 1차원으로 내리는 이 예시를 봅시다.
왼쪽처럼 차원축소를 하면 저 빨간 점들이 초록색 선으로 만들어집니다.
근데, 직선을 잘 돌려보면, 초록색 점들이 훨씬 더 퍼져있게 됩니다.
그러면, 오른쪽이 더 좋은 PCA 1차원이 됩니다.
그리고 그 PCA 1차원과 orthogonal한 축들 중 그 다음으로 퍼져보이는 PCA 2차원을 찾는거구요.
How to PCA
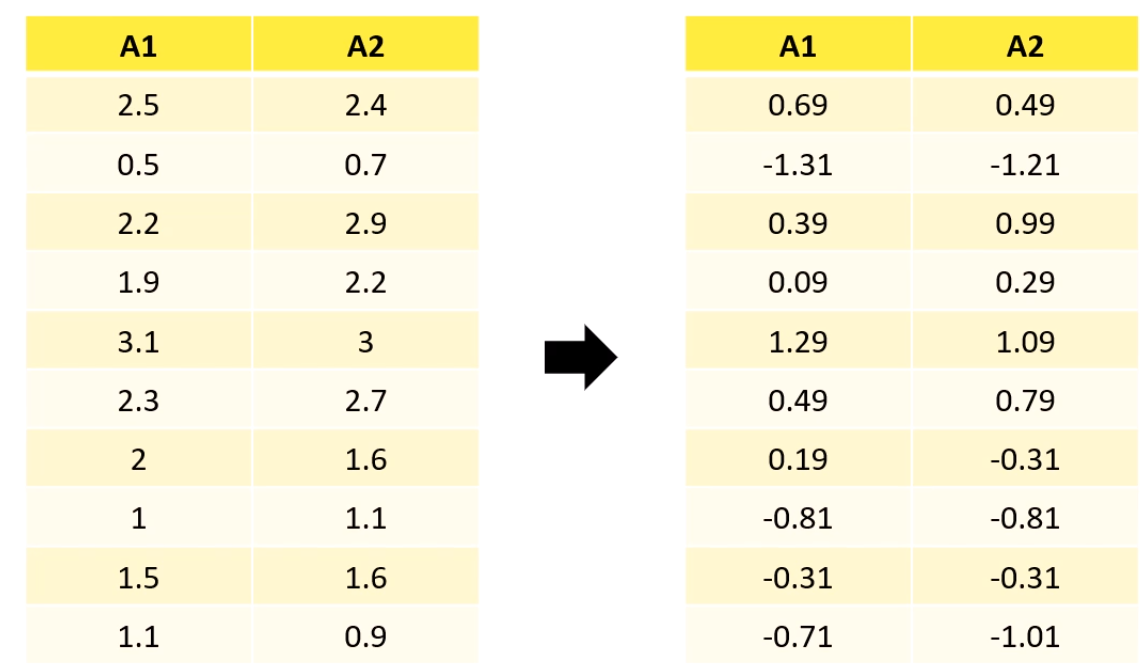
이런 2차원 데이터를 얻었다면,
각각의 평균을 다 빼주고,
바뀐 데이터에 대해 공분산행렬 를 계산합니다.
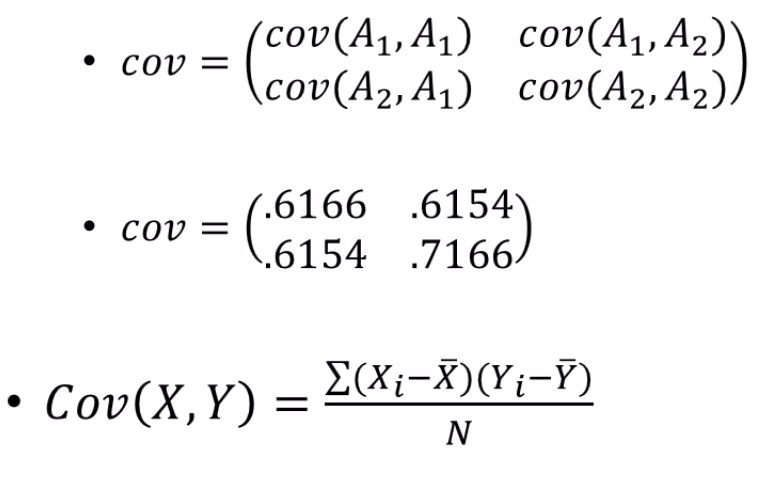
새로 계산된 에 대해 eigenvector와 eigenvalue를 구합니다.
그 중 eigenvector는 무한개 나오는데, 길이가 1인 친구를 택합니다.

이 때 구해진 eigenvalue가 데이터의 새로운 '분산'이며,
그 eigenvalue에 해당하는 eigenvector가 데이터의 PCA축입니다.
여기서는 1.2840이 분산이 더 크죠?
1.2840을 eigenvalue로 갖는 vector 가 PCA1축이고, 0.0491를 eigenvalue로 삼는 그 옆의 vector가 PCA2축입니다.
새 feature vector를 2개를 구했잖아요.
근데 우리가 2차원 데이터를 바탕으로 feature vector를 2개를 구했으니,
1차원으로 차원축소 하고 싶으면 feature vector를 1개만 써야 합니다.
그래서 기존의 data에 eigenvector를 곱해서 새 축으로 삼는거죠.
아까 eigenvalue가 크던 vector 만 남깁니다.

이건 걍 2차원 데이터를 2차원 데이터로 옮긴거니까 의미 없습니다.
그냥 축만 변환해준거에요.

2차원을 1개의 eigenvector만 곱해서 데이터를 변환해줍니다.
2차원 데이터 가 1차원 데이터 로 바뀌었죠?
이 scalar들이 수직선상 위에서의 데이터 위치가 됩니다.
정리하면,
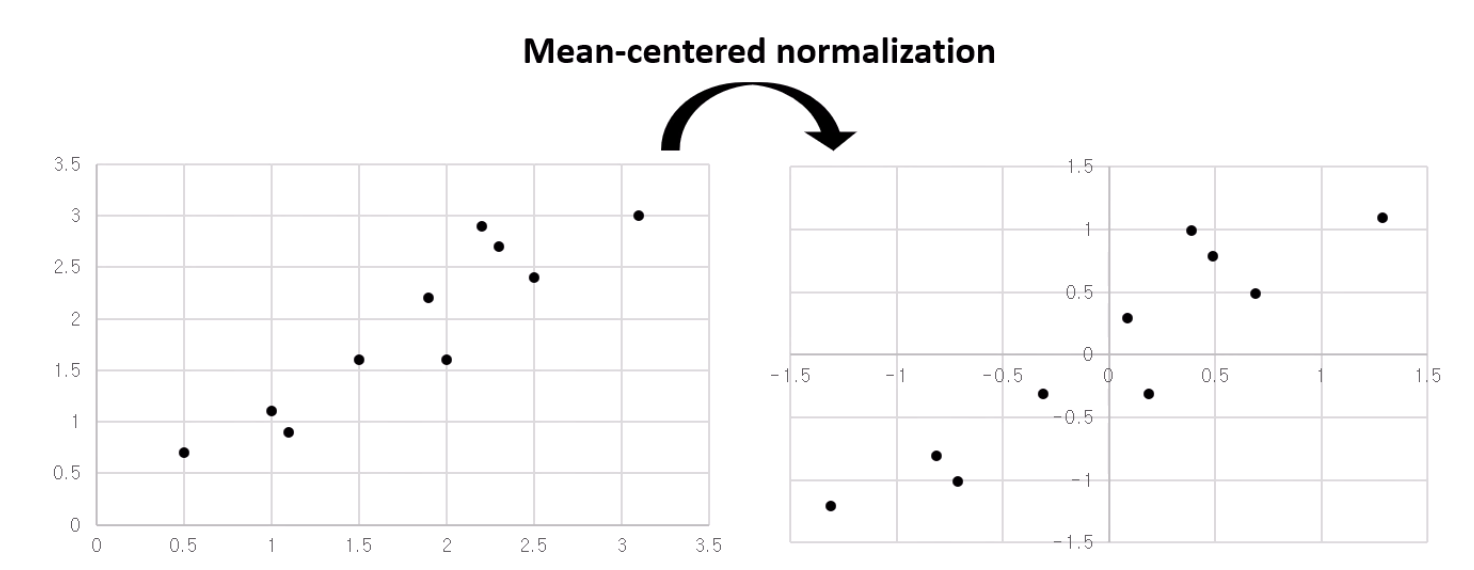
- 원래 데이터에서 평균을 다 빼서 Zero-centroid하게 만들어줍니다.
- 공분산행렬을 계산합니다.
- 공분산행렬의 Eigenvalue, Eigenvector를 계산합니다.
- 그 Vector를 가지고 representation합니다.
예를 들어서, 우리가 matrix A를 1차원으로 projection한다고 해봅시다.
Matrix A에 차원의 vector 를 곱한다고 할 때,
Matrix A의 각 instance들이 하나의 scalar로 표현이 되겠죠?
그 scalar들의 variance를 최대화하는 vector 를 찾는게 우리의 목표구요.
즉,
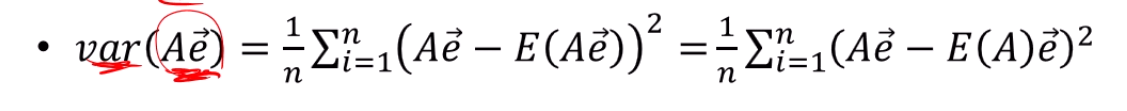
이 의 값을 최대화하는 것이 목표인데요.
분산의 정의를 이용하면 저렇게 정의가 되죠?
앞서 E(A)를 0으로 centralize 했구요.
그래서
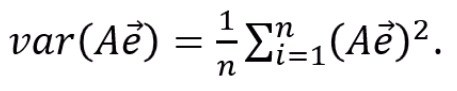
이렇게 정리가 됩니다.
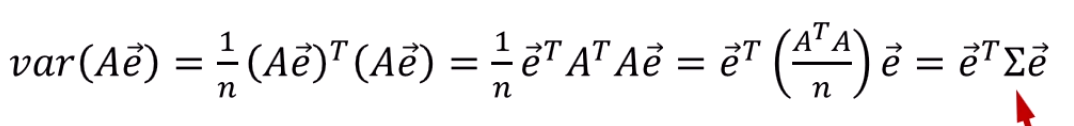
= 를 이용해서 전개를 해주고, 정리를 해주면
로 묶이는데,
이 공분산행렬 의 정의죠?
가 라는 제약조건이 있을 때 최대최소 조건을 구해야 한다면,
라그랑주 변환을 했었습니다.
이고,
미분을 해주면
이 되며,
와 같아지네요.
eigenvalue, eigenvector의 정의죠?
즉, 의 eigenvalue와 eigenvector를 찾아주면
그게 전체 분산을 최대화 하는 parameter들이 되겠네요.
Problem of PCA
가령, 4개의 축이 있고,
어느 데이터는 (x,y)축에서 원으로 표현되고,
어느 데이터는 (z,w)축에서 원으로 표현된다고 했을 때,
두 데이터를 동시에 표현하려고 하면,
PCA는 전체 데이터셋에 대해서 분산을 최대화하는 무언가만 고려하기 때문에,
데이터가 좀 뿌옇게 나올겁니다.
그런걸 개선한게 t-SNE입니다.
t-Stochastic Neighbor Embedding
PCA처럼 좌표의 선형조합을 해서 저차원 좌표를 찾는게 아니라,
데이터의 인접관계를 그래프로 모델링하고, 그 모델링한 그래프를 저차원으로 내립니다.
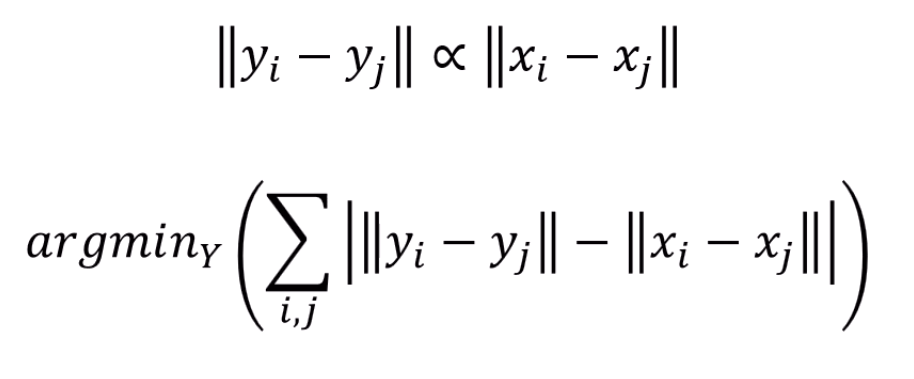
는 고차원 상의 점이고, 는 저차원 상의 점입니다.
일반적으로 는 2가 국룰입니다.
도식화하기 편하거든요.
아무튼, 그래서 2차원상의 점 관계가 100차원상의 관계와 얼추 비례하게,
즉 두 점들의 거리관계의 오차가 최소가 되는 의 집합 를 찾고자 합니다.
물론, 아예 이것과 같지는 않습니다.
유클리디안 거리를 재면, Loss function에 기여할 수 있는 거리가 달라집니다.
가령 엄청 떨어진 outlier가 존재하면, 그 점과 가깝게 매핑을 하는 것이 힘들어지고,
그 점때문에 loss function이 엄청 증가합니다.
또, Manifold learning 입장에서 생각해보면,
Manifold에서 가까운 애들은 상당히 큰 정보를 담고 있습니다.
가까운 애들이 objective function에 더 큰 영향을 끼치도록 해야 하는데,
실제로는 그렇지 못하다는거죠.
오히려 멀리 떨어진 애들이 objective function에 큰 영향을 끼칩니다.
그걸 보완하기 위해서 Gaussian Kernel을 적용합니다.
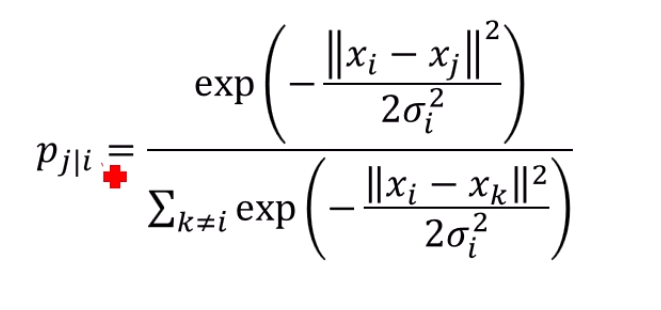
를 중심으로 한 gaussian kernel을 생각을 합니다.
그 kernel에서 에서의 pdf와 비례하게 거리를 정의하고자 합니다.
그걸 softmax를 normalize하듯이 모두의 합을 더한 값으로 나눠줍니다.
그럼 이 되겠죠? normalize 했으니까요.
즉, 확률론에서 가져와서, 두 점 사이의 euclidian 거리를 확률론적으로 바꿔주는 함수가 되겠습니다.
이러면 normalize도 되고, 멀리 있는 점들에게 패널티도 많이 주죠.
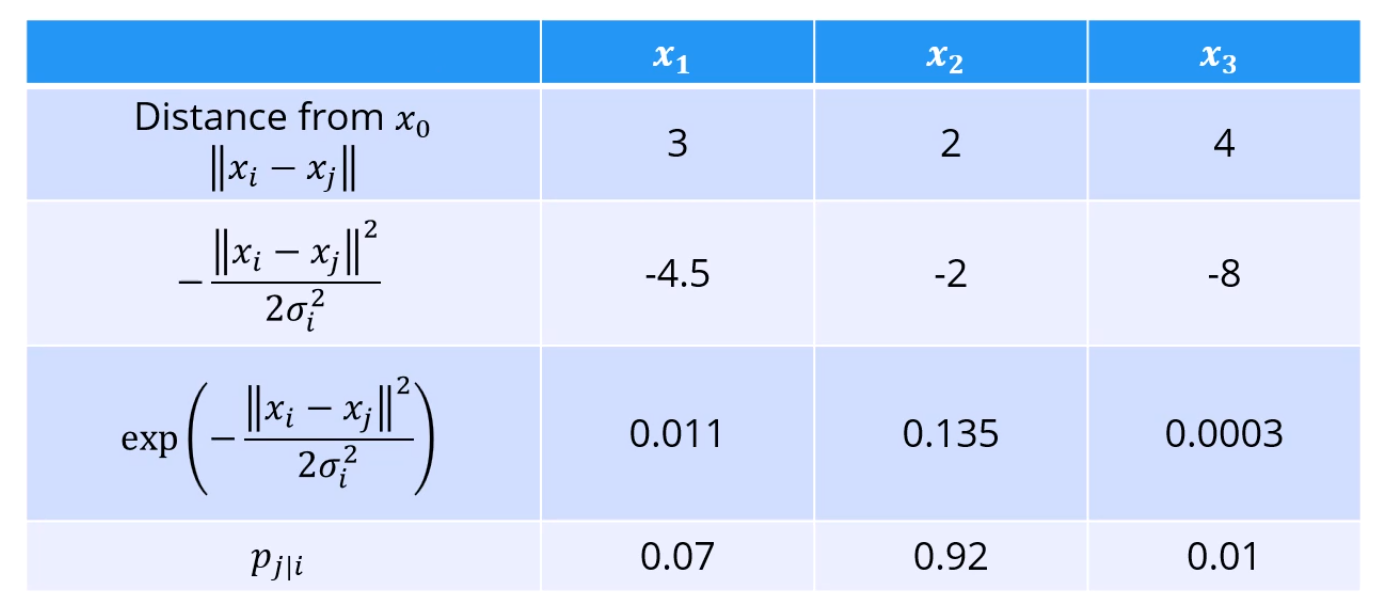
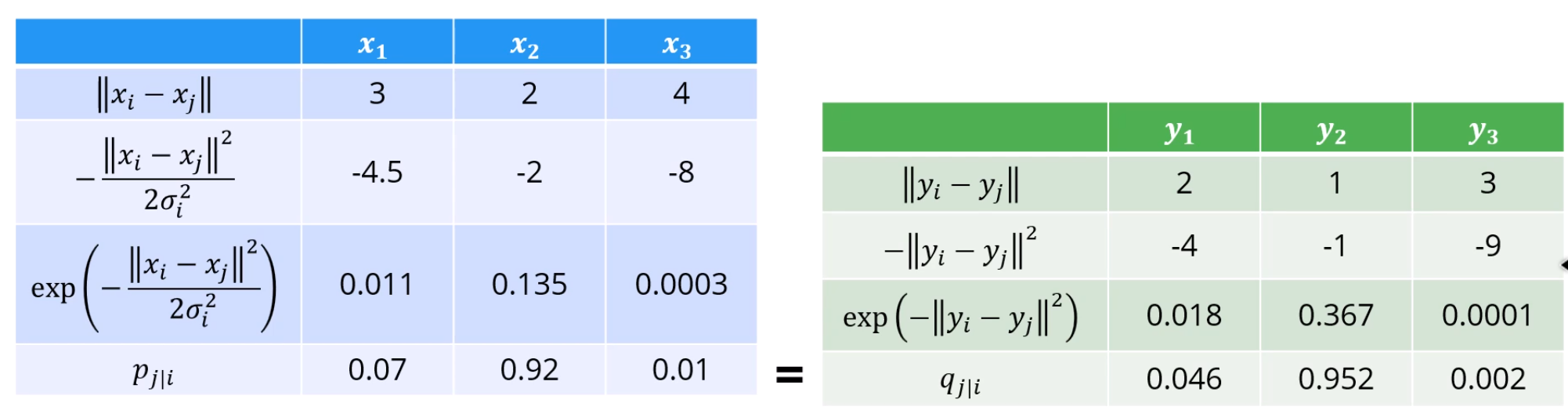
을 기준으로 한 거리가 3, 2, 4일 때,
로 가정을 할 때,
이것저것 계산을 하면
가까이 있는 에 대한 이고,
멀리 있는 에 대한 값은 0.0003이 됩니다.
정규분포에서 둘의 거리를 x좌표로 삼은 위치를 나타내는거에요.
그리고 normalize하면 가까운 애들은 0.92, 멀리 있는 애들은 0.01.
엄청 penality가 커졌죠?
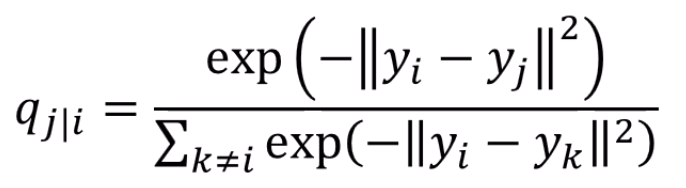
저차원상에서의 거리도, euclidian을 그대로 쓰지 않고 exp를 씌워 가까운 애들에게 이점을 줍니다.
normalize도 하구요.
차이는 gaussian kernel은 안 쓴다는 점이네요.
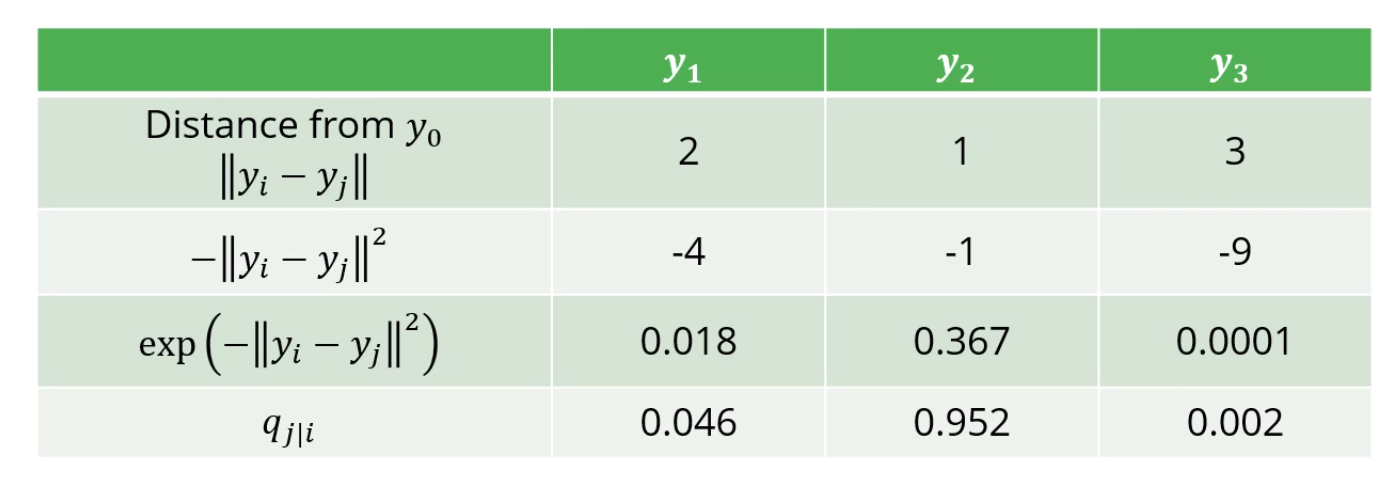
비슷하게 계산해보면 가 가까울수록 높죠?
이상적으로, 가 되게끔 하고 싶습니다.
즉, 라는 점에 대해 각 점 j와의 거리가,
100차원에서 표현됐을 때랑 2차원에서 표현했을 때랑 차이가 안 나게 하고 싶다는거죠.
다르게 말하면, P라는 분포와 Q라는 분포가 가까워졌으면 좋겠다는거에요.
이야,
여기서 KL Divergence가 나옵니다.
와 비슷하게 y의 분포를 바꾸는 문제로 귀결됩니다.
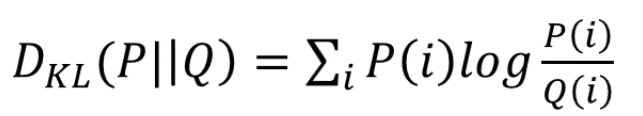
P와 Q의 분포가 같다면 KL Divergence는 0이 됩니다.
Divergence를 최소화하면 되겠죠?
즉, Cost function은 다음과 같습니다.
근데 의 의미가 뭡니까?
라는 점에서 떨어진 수많은 들에게 가중치를 알아서 부여해서 점수낸 분포죠?
즉 다음과 같이 해석됩니다.
Symmetrical SNE
와 는 대칭이 아닙니다.
입장에선 수많은 이웃들을 포함해서 의 값이 정규화가 되었습니다.
에게 가까운 이웃이 많다면, 의 거리가 상대적으로 penalize되겠죠.
입장에선 가 제일 가깝습니다.
그러면 는 에게 높은 점수를 줄거에요.
그래서 와 가 대칭이 안 되는 겁니다.
그래서 계산의 편의를 위해 로 두겠습니다.
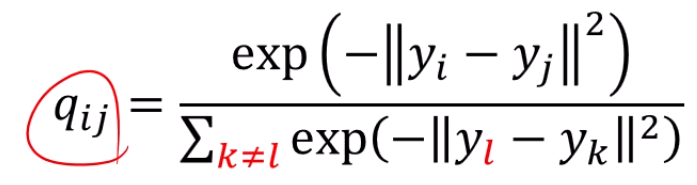
도 구현의 편의성을 위해 이렇게 바꿉니다.
여기서 cost function을 미분하고 gradient 구하고 stochastic gradient descent를 하면 되는데,
2가지이슈가 생깁니다.
- 는 어떻게 정하나요?
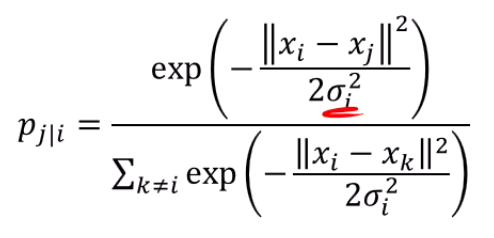
고차원 데이터를 normalize할 때 를 정하는 문제가 있습니다.
t-SNE에서는 해당 를 데이터의 분포도에 따라 adaptive하게 정합니다.
기준으로 데이터가 밀집하다면 를 작게 잡습니다.
기준으로 데이터가 sparse하다면 를 크게 잡구요.
penalize를 효율적으로 하기 위한 과정입니다.
그걸 통제하는 과정을 를 도입하여 씁니다.
를 도입합니다.
뭔가 엔트로피 식과 비슷하죠?
맞아요. 엔트로피 맞습니다.
아무튼 요약하자면, t-SNE에선 확률로 만들기 위해 Gaussian kernel을 각 점마다 씌우는데,
그 Gaussian Kernel의 크기가 문제가 되고,
그 크기를 점들간의 density로 정하게 해야 하는데,
그걸 엔트로피를 도입해서 가 되도록 Gaussian을 바꿔준다.
이렇게 봅니다.
- 고차원에선 공간이 많아서, 어떤 점과 애매하게 가까운 점이 많습니다.
그 애매한 점들을 훨씬 멀리 배치해야지
그나마 가까운 애들이 좀 더 가깝게 배치가 되게끔 표현이 가능합니다.
그걸 crowding problem이라고 부릅니다.
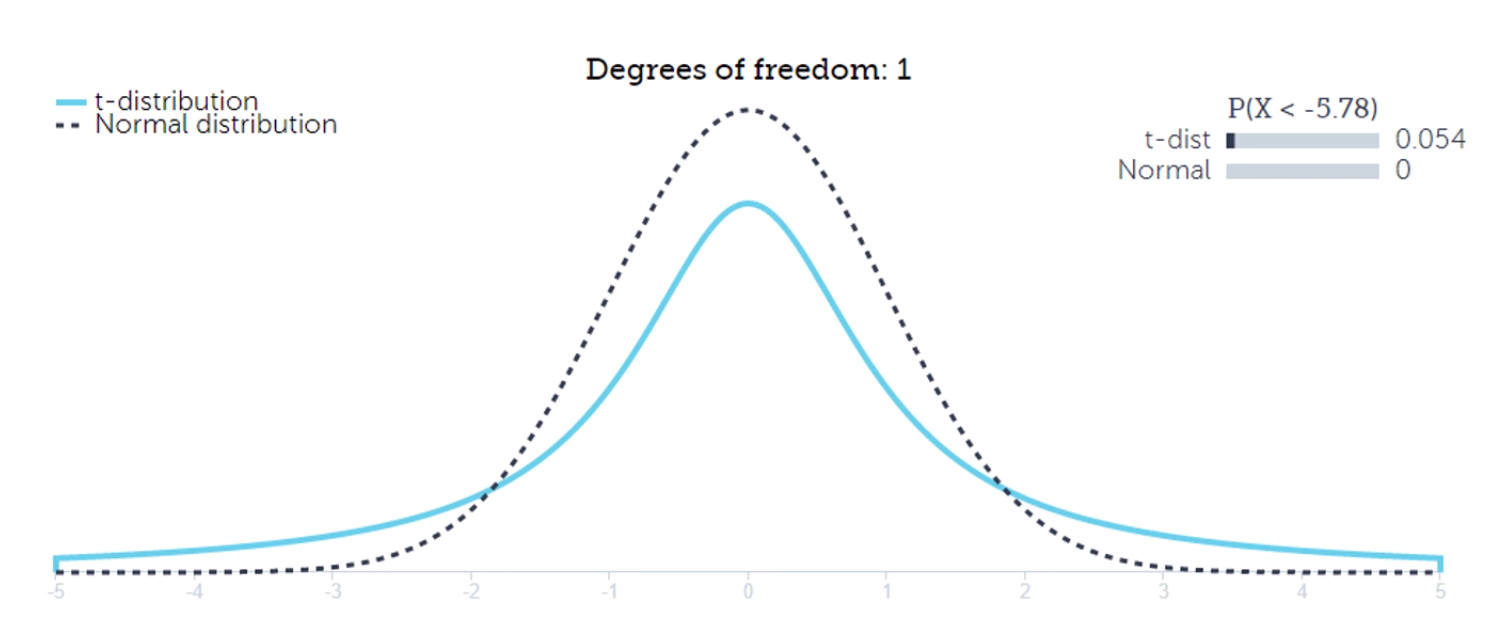
고차원에는 kernel을 씌우긴 하는데, gaussian kernel을 씌우고,
저차원은 t-distribution을 씌웁니다.
고차원에서 조금 멀리 떨어진 애들은,
저차원에서는 훨씬 멀리 떨어지게끔 표현이 됩니다.
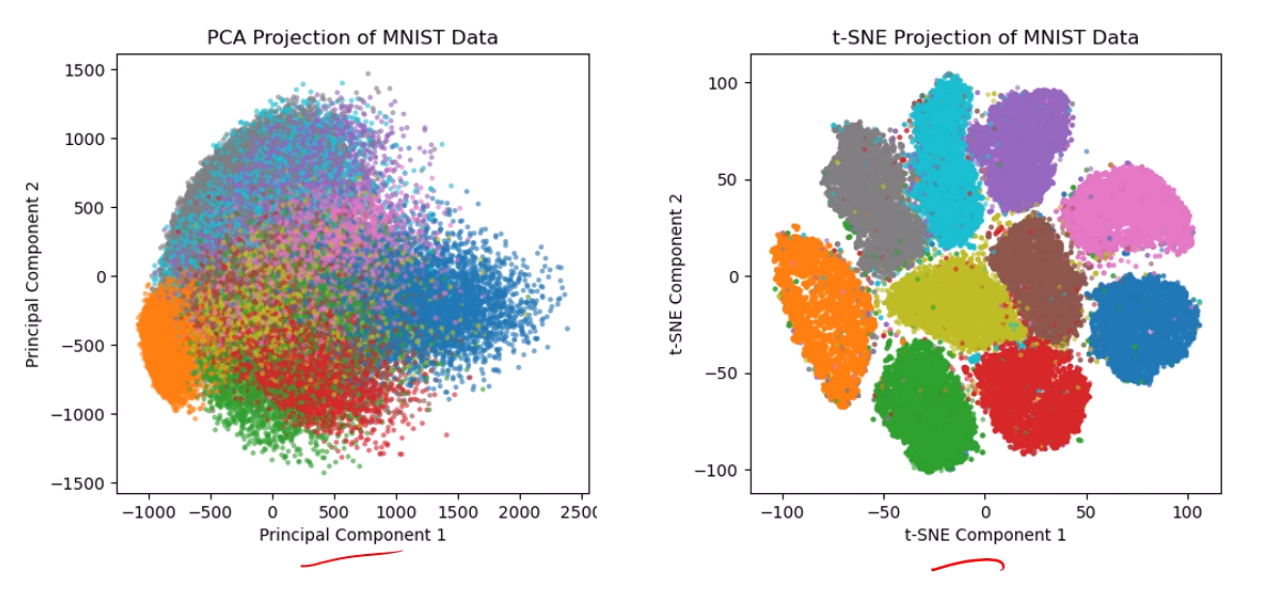
MNIST dataset을 clustering한 결과입니다.
PCA보다 t-SNE가훨씬 분류가 잘 되죠?
Be careful!
Non-linear dimensionality reduction 알고리즘에서 중요한 게 있습니다.

t-SNE에서 perp ()를 어떻게 잡냐에 따라서 데이터의 분포가 달라집니다.
원래 데이터에서 주황색은 파랑색에 더 가까운데,
그 절대적 거리가 반영이 안 됩니다.
그래서 Perp 30의 결과를 보고 '음, 클러스터들 끼리 같은 거리로 떨어져 있구나'
이건 매우 잘못된 해석입니다.
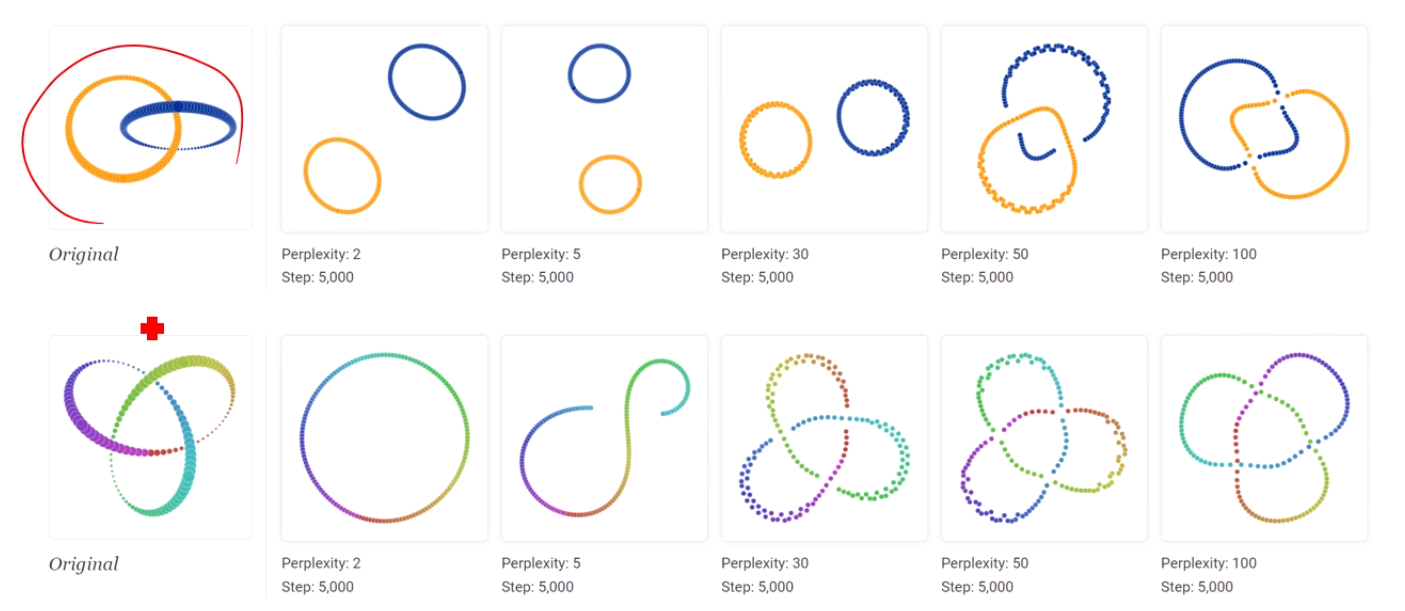
또한, Topology를 해석할 때에는 여러 parameter (여기서는 Perplexity)를 바꿔가며 해석해야 합니다.
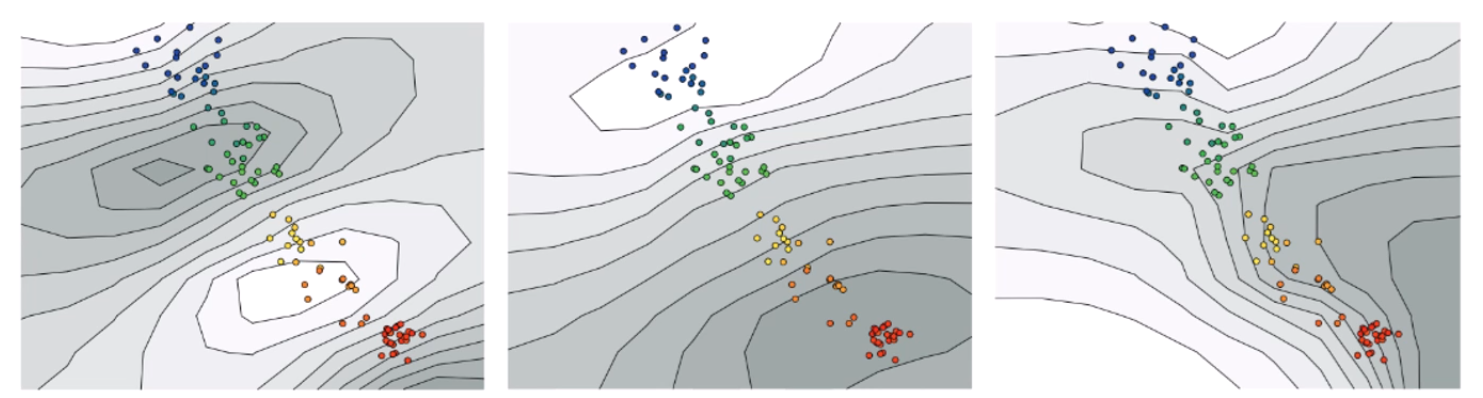
그리고, PCA와는 다르게 점들의 절대적 위치는 t-SNE에선 하등 의미가 없습니다.
PCA에선 축에 따라 분산도가 최대라는 의미라도 있었지,
t-SNE는 그런거 없습니다.
Recent Studies
DNN에서 차원축소 했을 때 Layer별로 차원의 수가 다릅니다.
그래서 서로 다른 차원의 데이터들을 비교 하는 것이 어렵구요,
차원축소 시 데이터의 왜곡이 생깁니다.
귤을 까는걸 생각하면, 귤의 꼭지를 기준으로 쭉 깐다면,
까져서 평평해진 귤껍질의 boundary는 사실 하나의 점이었을 가능성이 높습니다.
약간 전개도 생각하면 됩니다.
그래서, 2차원상에서 멀어보여도 실제로는 같은 / 비슷한 데이터일 수 있는거죠.
이것저것 해결해보려고 노력한 알고리즘들로
Joint t-SNE, UMAP, GhostUMAP 등의 최신 연구들이 많습니다.
