Support Vector Machine (SVM)

조금 오래된 분류 모델이긴 합니다.
SVM은 '수학적으로' 이해하기가 좀 힘듭니다.

이론적인 background를 잘 이해를 해봅시다.

$f(x) = f(x_1, x_2, ... , x_d)$같이 미분 가능한 objective function이 있다고 합시다.

이 함수에 대해 제약이 없이 최솟값을 찾고 싶다면,
미분해서, gradient가 0이 되는 지점, 즉 $\frac{\partial f}{\partial x_i} = 0$이 되는 점들을 찾으면 '최솟값' 이 될 가능성이 존재하게 됩니다.

근데, 추가적인 constraint가 존재할 때 최솟값을 찾고 싶다면요?

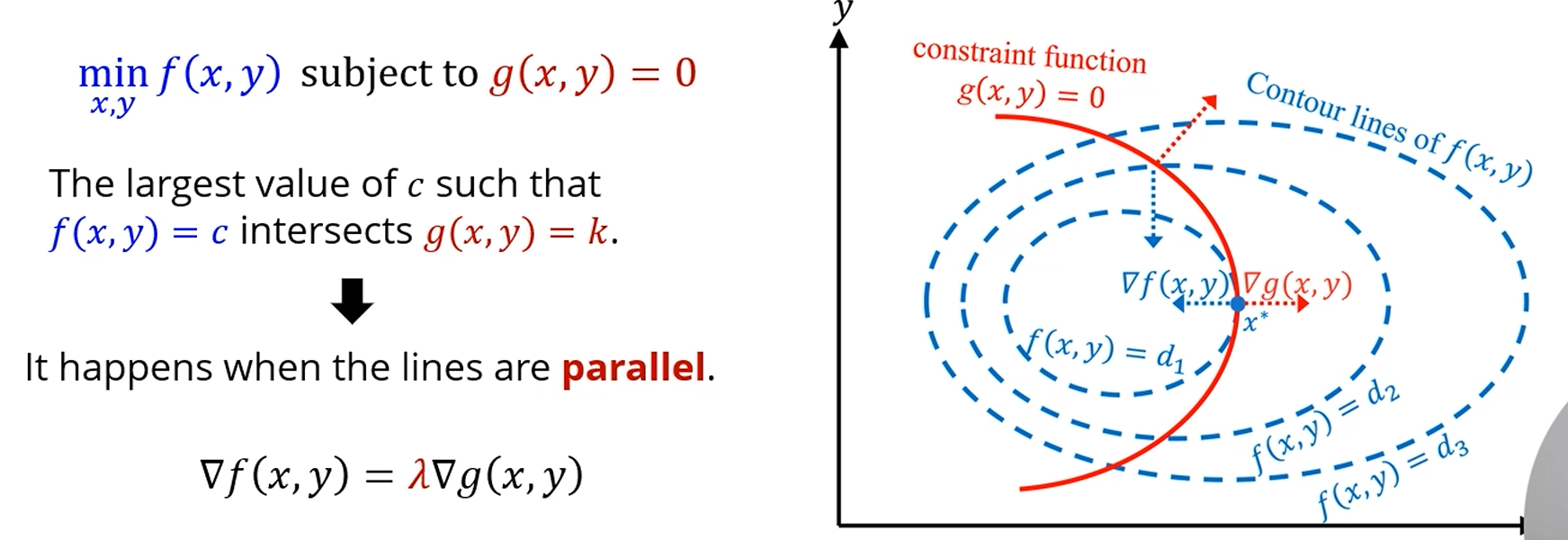
$f(x,y)$에 대해 최솟값을 찾는데, $g(x,y) = 0$을 만족하는 점 내에서 최솟값을 찾고 싶다면,
'라그랑지안'을 정의해서 풀었습니다.

$f(x)$를 최소화 하는 $x$를, $g_j(x) = 0, j = 1, 2, ... , k$일 때 찾고 싶습니다.
$L(x,\lambda) = f(x) + \sum_{j=1}^k\lambda_jg_j(x)$로 표현할 수 있습니다.

이 $L$에 대해 gradient를 구하면 minimum이 될 수 있죠.

$f(x)$ + 각 조건에 대한 $\lambda$ * 각 조건식 $g(x)$를 하면 그게 $L(x)$가 되고,
그걸 미분하는 거였습니다.
어렵지는 않아요.

$x^2+y^2 = 1$을, $x+y=1$의 제약조건 하에서 최소화시키는 $x,y$를 찾고싶다면?
$L(x,y,\lambda) = (x^2+y^2-1) + \lambda(x+y-1)$로 정의하고,

이 식의 $x, y, \lambda$에 대한 gradient를 구하면 됐죠?
$\frac{\partial L}{\partial x} = 2x+\lambda$
$\frac{\partial L}{\partial y} = 2y+\lambda$
$\frac{\partial L}{\partial \lambda} = x+y-1$이고, 이 식들이 전부 0이 되게 연립하면
$x,y,\lambda$를 얻을 수 있었습니다.

$x^2+y^2+z^2$를 $x+y=2, x+z=3$의 제약조건 하에서 최소화한다면요?
$\lambda$를 2개 쓰면 되죠.

$L(x,y,z,\lambda_1,\lambda_2) = (x^2+y^2+z^2)+\lambda_1(x+y-2)+\lambda_2(x+z-3)$으로 세우고,

그래디언트 5개 구해서 연립하면 됐습니다.

그러면, 조건이 부등호로 주어졌다면요?

$x^2$를 $x\geq b$의 조건에서 최소화하는 $x$를 찾는다면요?
$b$의 값에 따라서 최솟값이 달라지겠죠?

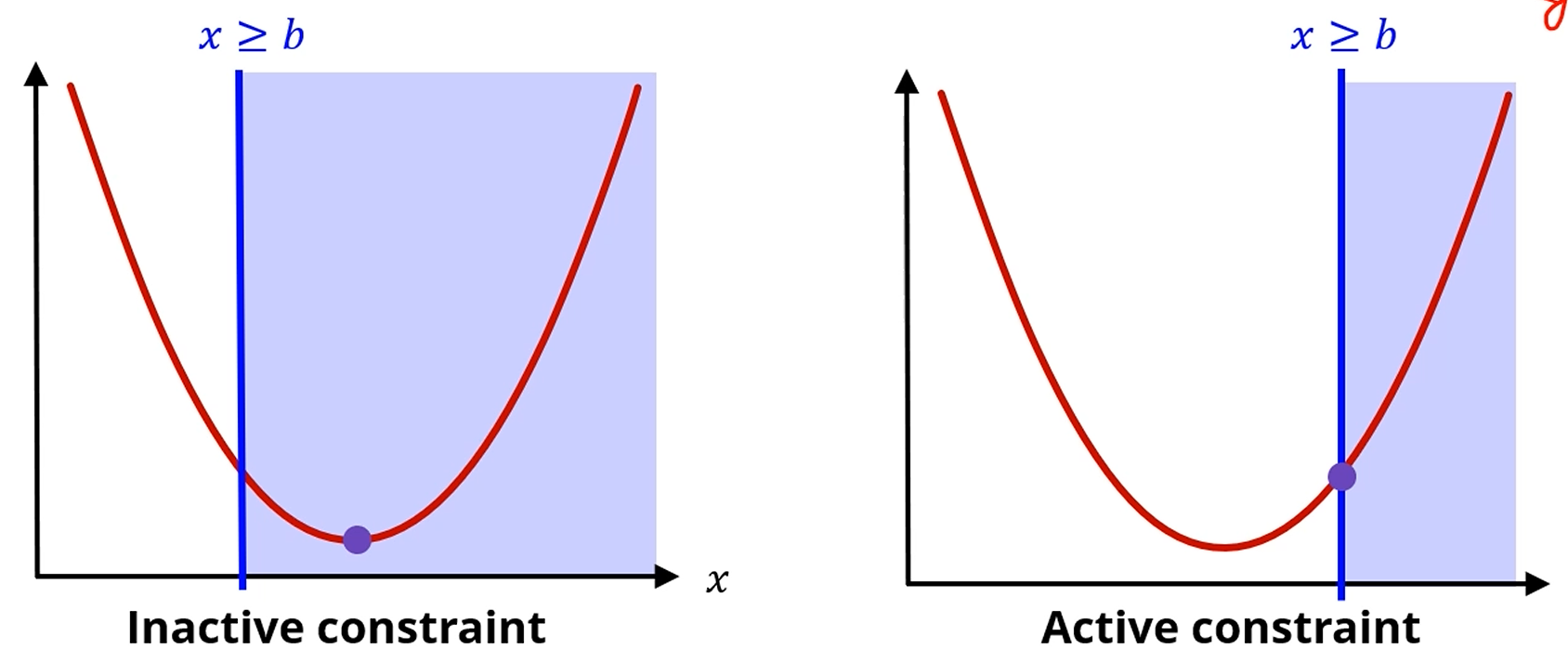
$b<0$이라면 조건이 있으나 없으나 최솟값은 0이죠?
그러면 이 constraint가 활성화되지 않았으니, Inactive constraint라고 칭합니다.
반대로 $b \geq 0$이라면 constraint가 활성화 되었죠.

조금 일반적으로 따져봅시다.

$f(x)$를 최소화하는 $x$를 찾고 싶은데, 조건이 2개 붙습니다.

$g_i(x) = 0 , i = 1 ... k$가 하나구요,
$h_j(x) \leq 0, j = 1 ... m$이 하나입니다.

중요한 점은 이 $\leq$인데, 만약 $h_j(x) \geq 0$을 풀고 싶다면, -1을 곱해서, 항상 부호를 $\leq$로 만들어 생각해야 합니다.

또 편의를 위해 모든 함수는 convex하다고 정의합시다.

이러면, 라그랑지안을 다음과 같이 정의할 수 있습니다. ($\mu \geq 0$)

$L(x, \lambda, \mu) = f(x)+\sum_{i=1}^k\lambda_ig_i(x) + \sum_{j=1}^m\mu_jh_j(x)$

이 때 $\lambda = (\lambda_1, \lambda_2, ... , \lambda_k)$를 Lagrange Multiplier (라그랑주 승수),
$\mu = (\mu_1, \mu_2, ... , \mu_m)$을 KKT Multiplier라고 칭합니다.

원래 $f(x)$와 $L(x,\lambda,\mu)$의 관계가 어떻게 될까요?

우선, $f(x) \geq L(x, \lambda, \mu)$가 성립합니다.

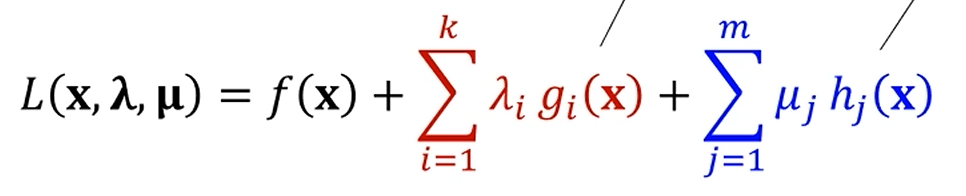
빨간 식은 정의상 $g_i(x) = 0$이고,
$h_j(x)$도 0 또는 음수죠?
$\mu_j$도 0 또는 양수에요.

원래 식으로 돌아옵시다.

$f(x)$가 최소가 될 때의 $f(x)$의 값을 $f^*$로 칭합니다.

그러면,
$f^* = \text{min}f(x) \geq \text{min}L(x,\lambda,\mu)$가 성립하죠.

그 최소화 된 $f(x)$에 넣은 x를 대입한 라그랑지안 $\text{min}L(x,\lambda,\mu)$를 $g(\lambda, \mu)$라고 합시다.

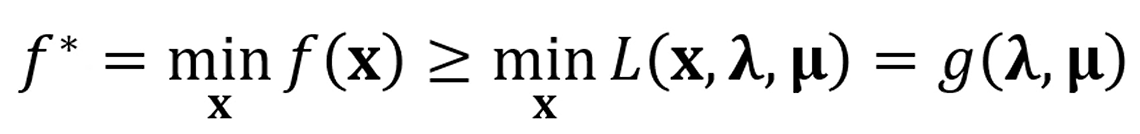
다음과 같은 식이 성립하죠?
여기서 얻을 수 있는 내용은,

$f^*$는 항상 $g(\lambda, \mu)$보다 크거나 같은 거고,
$\lambda, \mu$가 뭐가 들어가도 $f^*$는 $g(\lambda, \mu)$보다 크거나 같다는 거고,

$\lambda, \mu$를 잘 조합해서 $g(\lambda, \mu)$를 최대화 하더라도 $f^*$는 그거보다 크거나 같다는 거고,

다르게 쓰면
$f^*$는 $\text{max}_{\lambda, \mu \geq 0} \text{min}_x L(x,\lambda,\mu)$보다 항상 크거나 같다는 거고,

f(x)를 최소화하는 x와,
그걸 $L(x,\lambda,\mu)$에 넣었을 때의 함수 $g(\lambda, \mu)$를 최대화 하는 $\mu, \lambda$를 전부 대입한
$L(x,\lambda,\mu)$를 $g^*$라고 두면,

$f^* \geq g^*$도 성립합니다.

뭐 당연한 거에요. 정의를 그렇게 했습니다.

Duality

어떤 함수의 최솟값은, 그 함수의 라그랑지안의 최솟값의 최댓값보다 크거나 같다.

이 관계를 Weak Duality라고 부릅니다.

근데, 특정한 경우, $f^* = g^*$가 성립합니다.
이 경우는 좋아요.
$f^*$가 궁금할 때, $g^*$만 찾아도 되니까요.

이 경우는 $f$가 convex하고, 모든 등호 조건이 affine하며, (상수함수던가, 증가함수) 모든 부등호 조건도 convex하다면 $f^* = g^*$가 성립합니다.

이 condition을 Slater's condition이라 부르며,
이걸 Strong Duality라고 부릅니다.

이게 성립하면 $f^*$를 구할 때 $g^*$를 구하면 되는거죠.

그게 의미가 있나요? 어차피 max min 다 구해야 하잖아요.

있어요! 추후에 많이 볼겁니다.

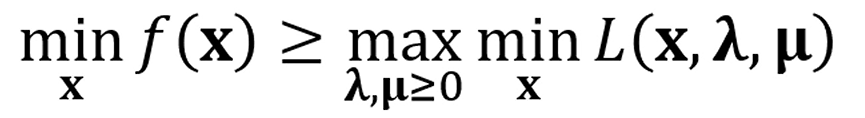
duality를 풀어서 썼습니다.

흠, 근데 $f$랑 $L$이 둘 다 있는게 불편합니다.

여기서, 우리는
$minf(x)$를 $\text{min}_x \text{max}_{\lambda, \mu \geq 0} L(x,\lambda,\mu)$로 나타낼 수 있습니다.

라그랑지안의 정의에서, x가 infeasible ($g_i(x)=0$이나, $h_j(x) \leq 0$)을 위배하는 경우,
$\lambda, \mu$를 잘 조져서 $L(x,\lambda,\mu)$를 $\inf$로 만들 수 있겠죠.

그리고 x가 feasible하는 경우에 $L(x,\lambda,\mu)$의 최댓값은
$\mu_j = 0$인 경우, $L(x,\lambda,\mu)$ = $f(x)$인 경우밖에 없겠죠?

즉,$\lambda, \mu$를 자유롭게 조정할 때 $\text{max} L(x,\lambda,\mu)$는 $f(x)$입니다.
그러면
$minf(x)$ = $\text{min}_x \text{max}_{\lambda, \mu \geq 0} L(x,\lambda,\mu)$
가 성립하죠.

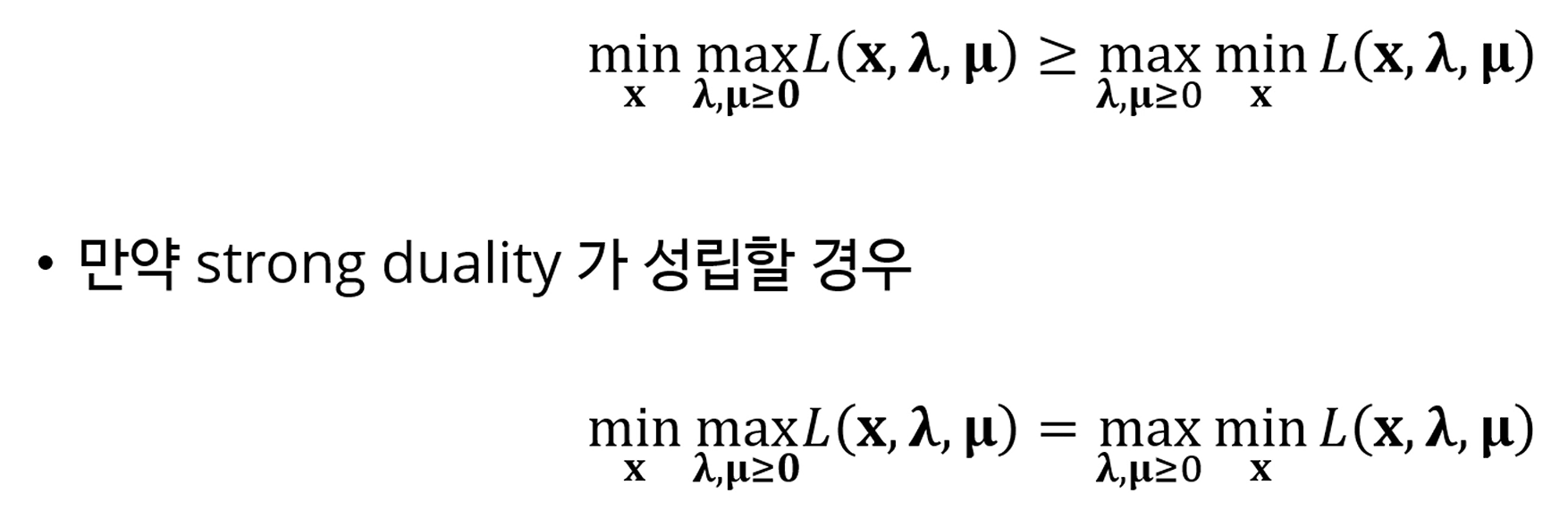
이렇게 되죠?
좌항이 $f^*$고, 우항이 $g^*$입니다. 단지, $f(x)$가 들어간게 못생겨서 $L(x)$로 치환했을 뿐이에요.

그래서, 이런 문제가 존재하면,

max와 min을 뒤집어서 풀 수 있다. 라는 정리입니다.

밑의 Dual form으로 바꾸면 간단해져요.

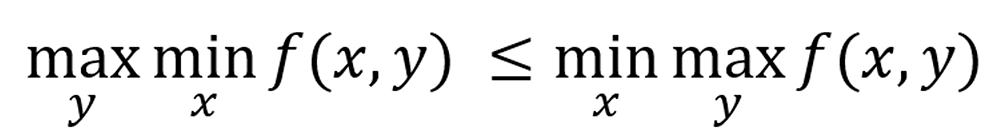
이런 부등식을 minimax inequality라고 부릅니다.

바르셀로나에서 젤 못하는 놈이, FC성균관에서 젤 잘하는 놈보다 잘하거나,
일부 컨디션에서는 똑같다.
이렇게 이해하면 좋아요.

KKT Conditions

아이고, 그래요.
원래 하던거로 돌아와봅시다.

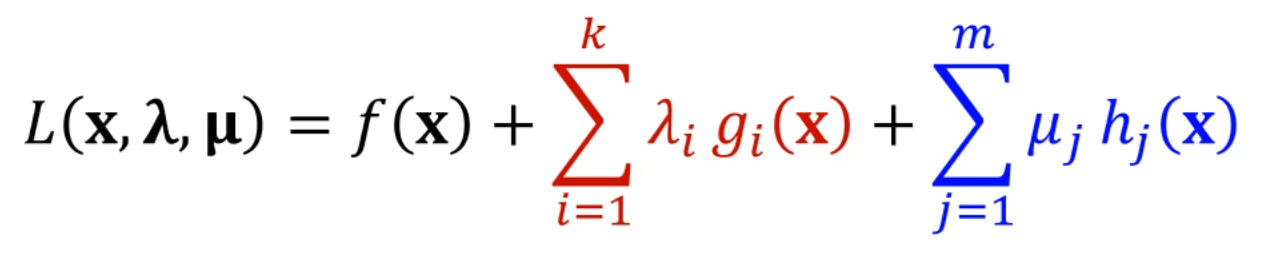
이거 라그랑지안 정의를 했는데,
이걸 풀 때,
$x$가 최솟값이 될 수도 있는 조건이 있습니다.

점 $x$에서 L의 gradient가 0이어야 하고,
g, h에 대해 아까 언급한 feasibility가 만족되어야 하고,
$\mu_j \geq 0$도 만족되어야 하고,
마지막으로 $\mu_j h_j(x) = 0$도 항상 만족해야 합니다.

이 4가지 조건을 KKT Condition이라 부릅니다.

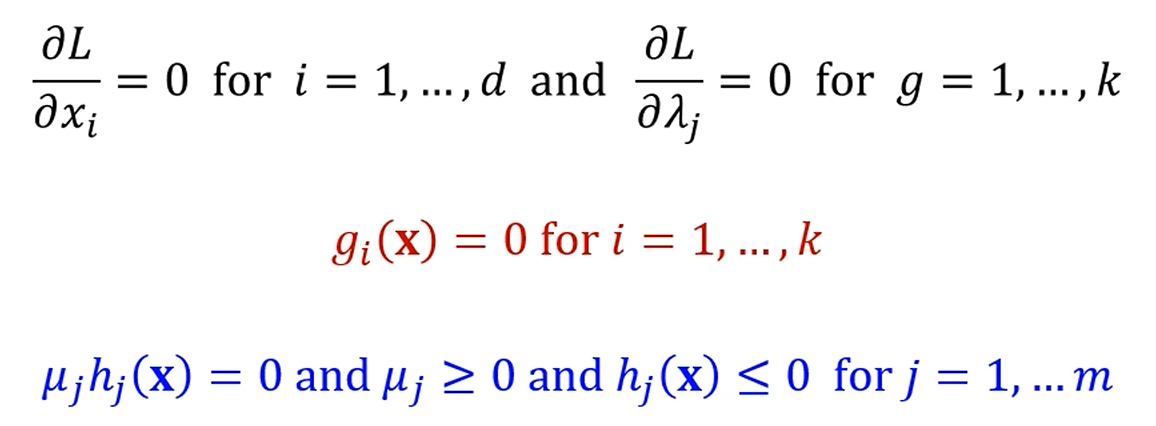
그래서 정리하면 KKT Condition은 다음과 같습니다.

이것들을 다 만족해야 최솟값이 될 가능성이 생깁니다.

구체적인 예시를 볼까요?

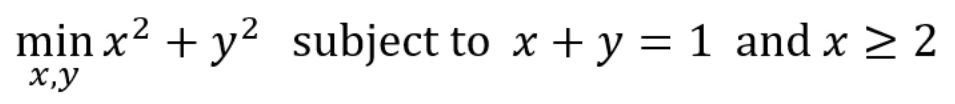
이거 풀어봅시다.

부등호 식은 $\leq$로 바꿔야 한다고 했죠?

그러면 이 식은
$L(x,y, \lambda,\mu) = (x^2+y^2) + \lambda(x+y-1) + \mu(-x+2)$가 됩니다.
이 때 $\mu \geq 0$은 성립해야겠죠.

이 식을 $x, y, \lambda$에 대해 미분하고, $\mu$에 대해서는 따로 체크합니다.

$\frac{\partial L}{\partial x} = 2x+\lambda-\mu = 0$
$\frac{\partial L}{\partial y} = 2y+\lambda = 0$
$\frac{\partial L}{\partial \lambda} = x+y-1 = 0$

추가로 KKT Condition에 의해,
$\mu(-x+2)=0$, $-x+2 \leq 0$이 성립합니다.

케이스를 나누면,
$\mu = 0$이라면,

이 4개를 다 만족해야 하고,
$\mu \neq 0$이라면,

을 다 만족해야 합니다.

Case 1에 대해 연립해보면, $x=0.5, y=0.5, \lambda=-1$이 나오니까,
$-x+2\leq0$에 위반되죠? infeasible합니다.

Case 2에 대해 연립해보면, $x=2, y=-1, \lambda=2, \mu=6$이 나옵니다.
feasible합니다.

해당하는 x, y를 넣으면 $x^2+y^2$는 주어진 조건 하에서 최솟값이 $5$네요.

이 문제도 풀어볼까요?

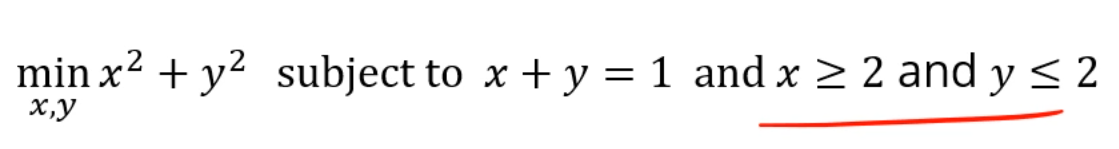
식으로 표현하면
$L(x,y,\lambda,\mu_1,\mu_2) = (x^2+y^2)+\lambda(x+y-1)+\mu_1(-x+2)+\mu_2(y-2)$
가 될거구요,

싸그리 싹 싹 그래디언트를 구해주면,

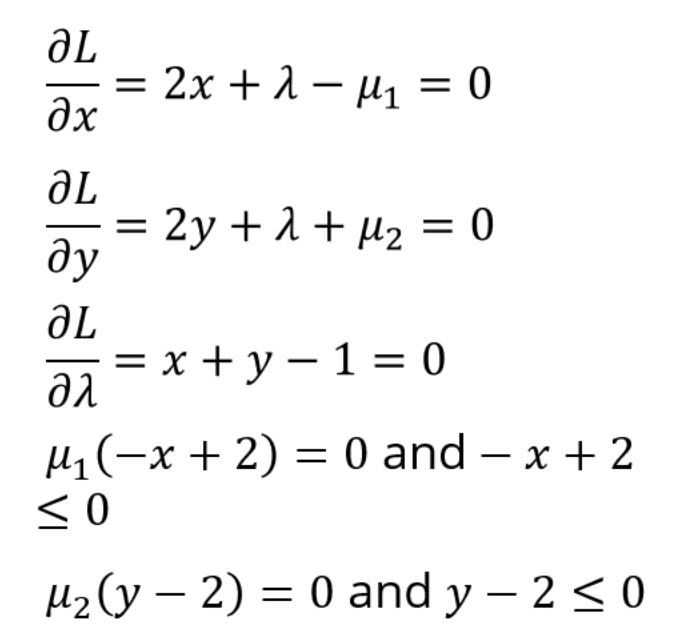
다음과 같은 조건들을 다 연립하면 되는데,
우리는 $\mu_1, \mu_2$에 대해서 각각이 0일 때와 0이 아닐 때, 총 4개의 케이스를 분류해야 합니다.

이래저래 연립을 해주면, infeasible한 솔루션들이 존재하게 되고,
feasible한 답만 골라주면 됩니다.

SVM

Motivation

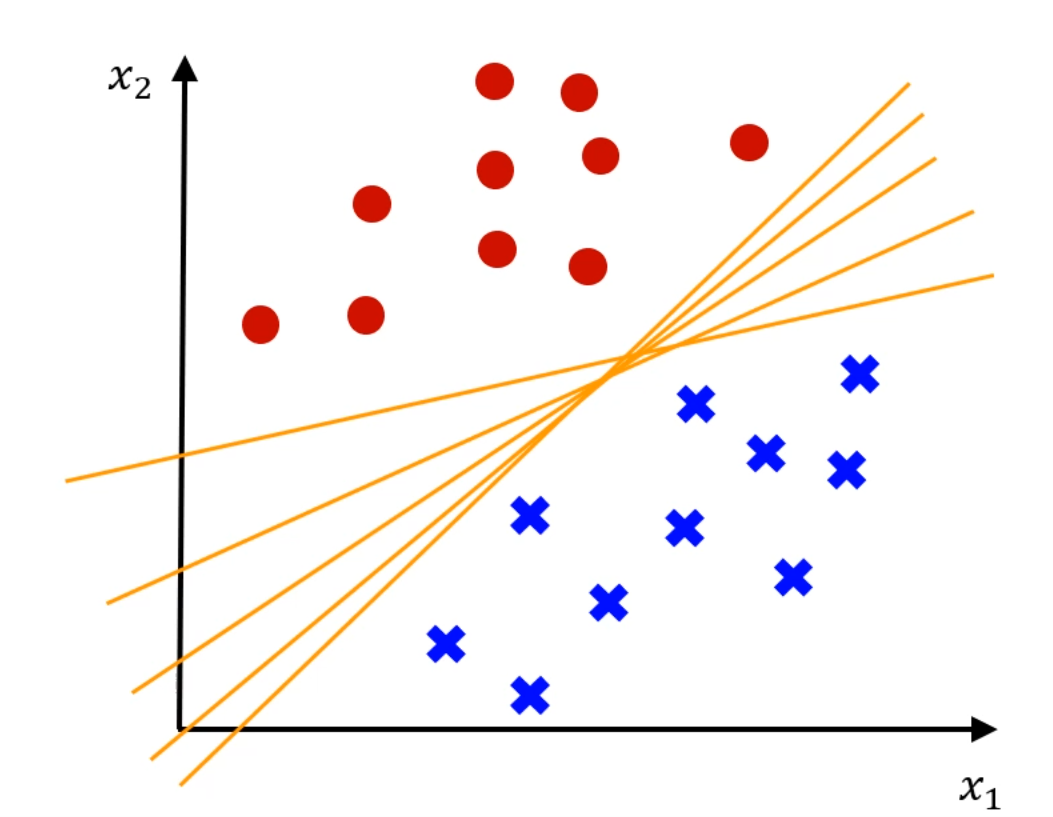
확률같은거 쓰지 말고, 최적의 decision boundary를 어떻게 정할까요?
이 중에서 '좋은 boundary'와 '나쁜 boundary'가 존재합니다.

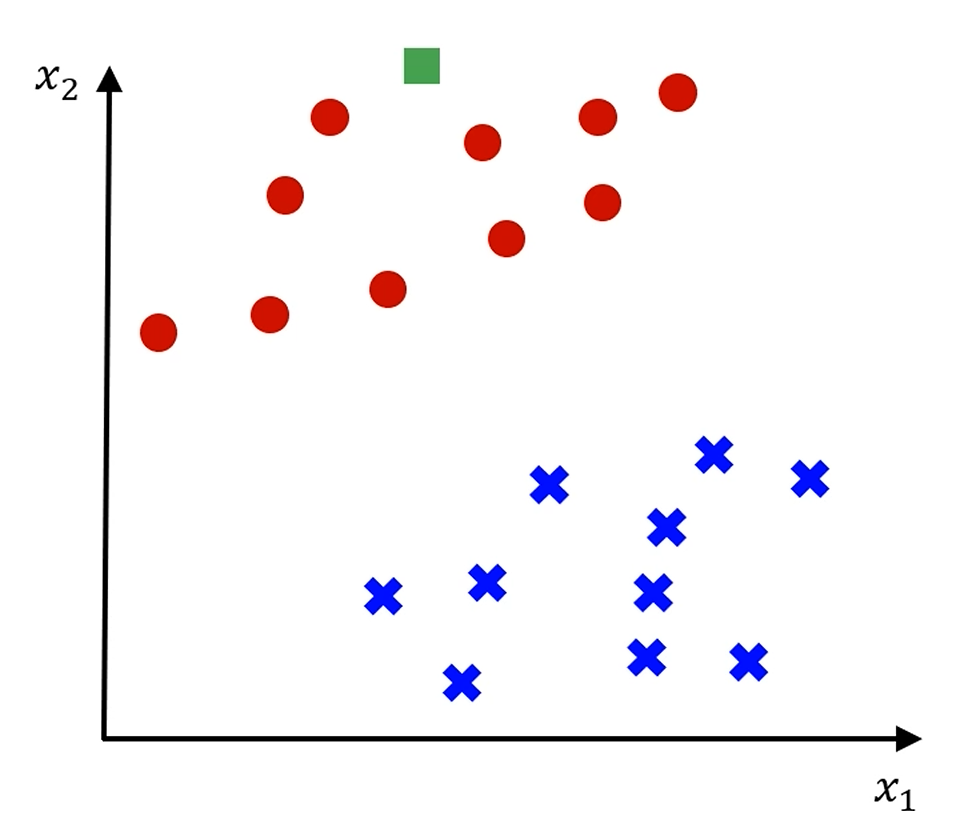
선은 고려하지 말고,
저 초록색 샘플은 선이 어떻게 그어지든 아마 '빨간색'으로 분류가 되겠죠?

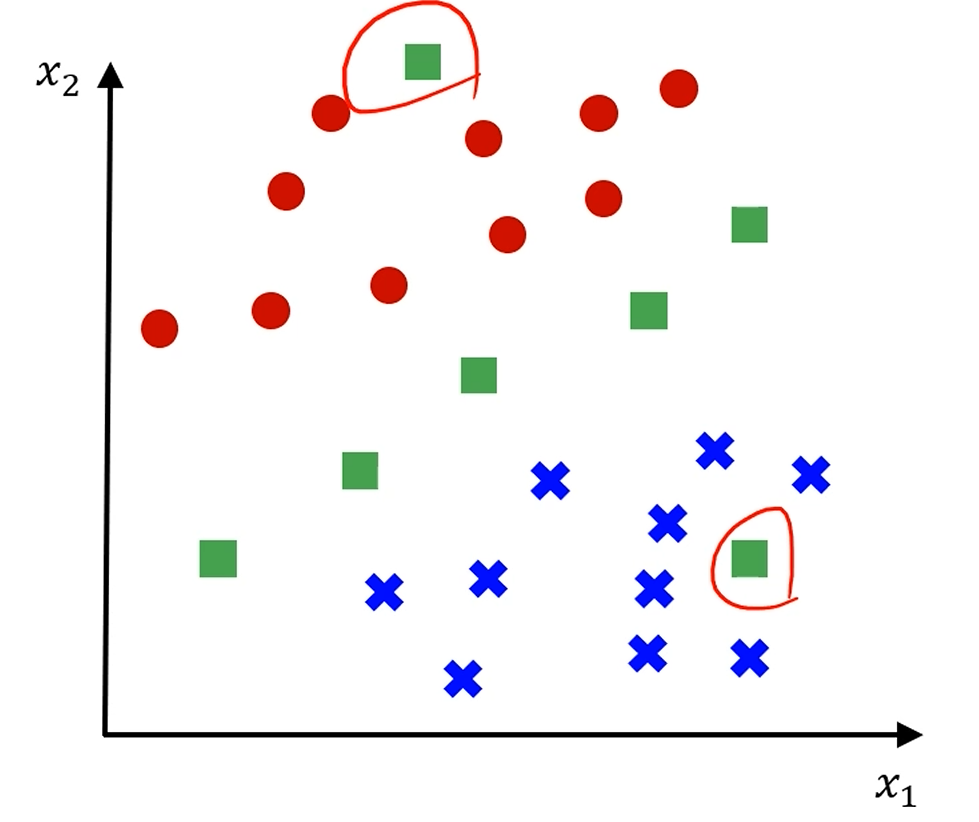
이 가운데에 있는 애매한 샘플들은 선을 어떻게 긋냐에 따라 빨강이 될 수도, 파랑이 될 수도 있습니다.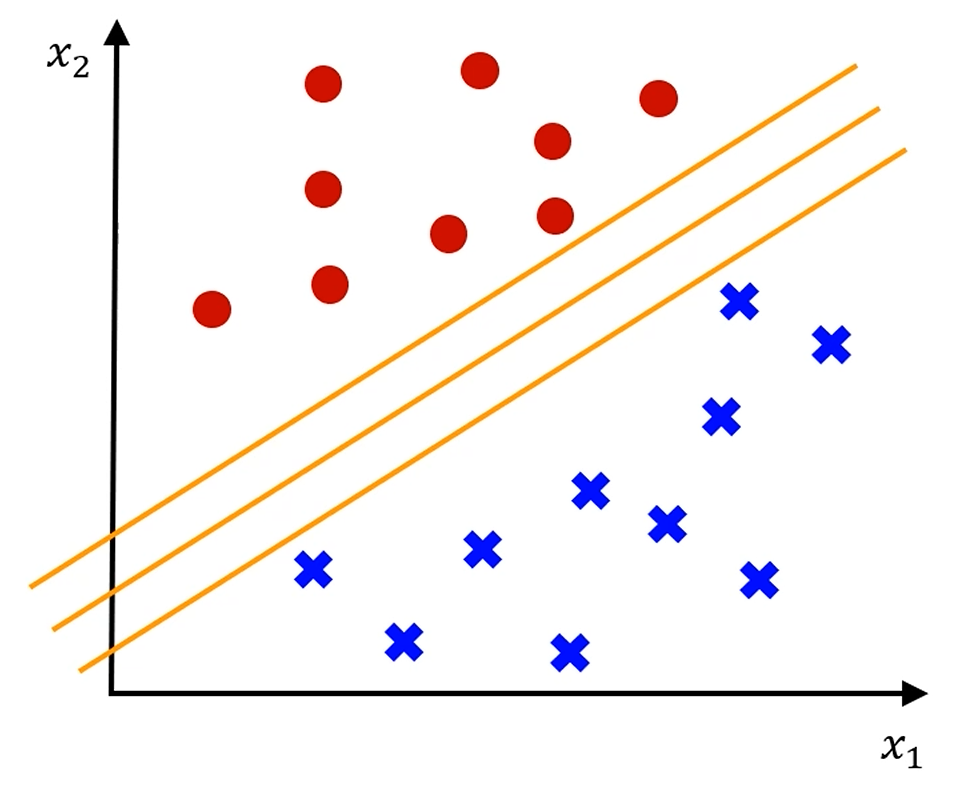

그나마 이 중에는 '가장 가운데' 있는 선이 제일 공평해보이죠?

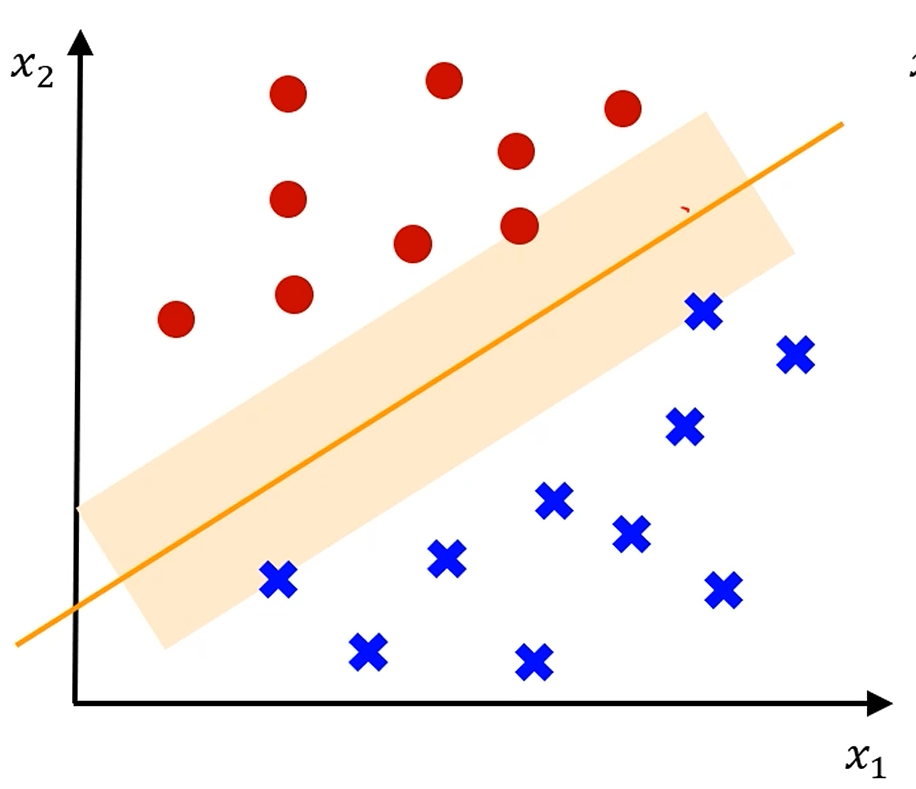
빨강 점 중 가장 가까운 샘플과,
파랑 점 중 가장 가까운 샘플의 '간격'이 최대가 되게끔 선을 그어야 합니다.

그리고, 우리는 저 색칠된 Margin이 최대가 되는 선을 원합니다.

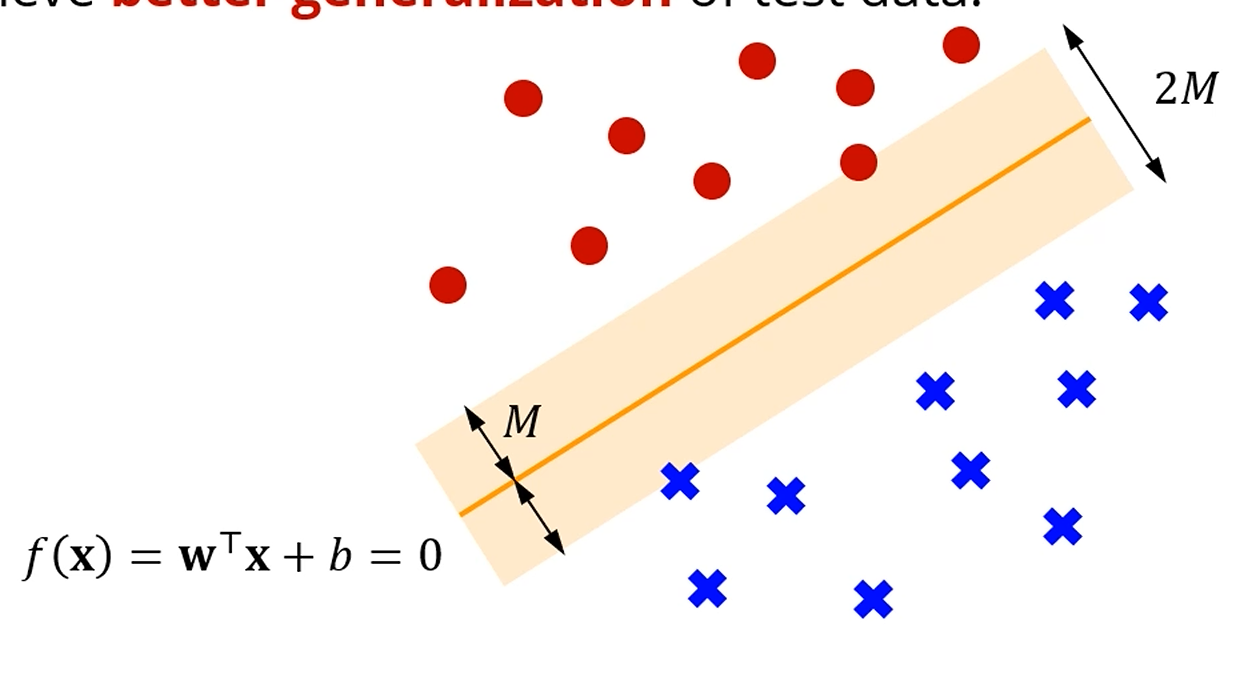
우리가 찾고 싶은 hyperplane 중 최적의 hyperplane은,
각 class로부터 우리가 찾은 평면 사이의 거리, 즉 margin이 최대가 되는 hyperplane을 찾고 싶구요,

그 사이에 정확히 절반이 되는 지점에 평면을 만들고 싶습니다.

그러면 그 'Margin'은 어떻게 재나요?

$f(x) = w^Tx + b$일 때,
특정 점 $[x]$를 가정해 보면,

그 점 $[x]$와 평면 사이의 거리는, 수선의 발의 거리겠죠?

$x = x_p + d\frac{w}{||w||_2}$가 성립합니다.

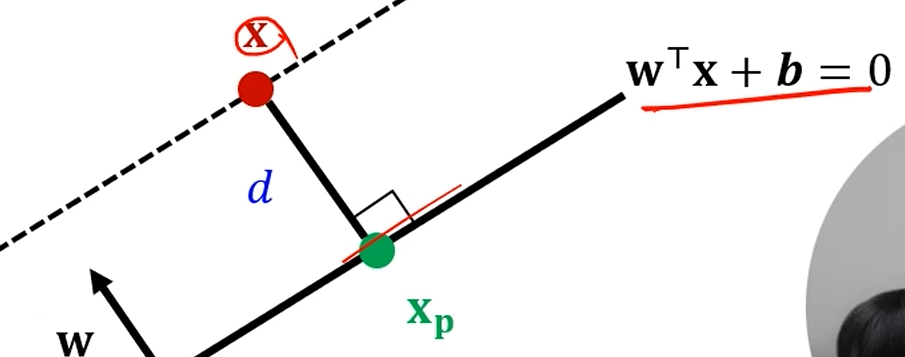
$\frac{w}{||w||_2}$는 법선 유닛벡터구요.

그 x를 $f(x) = w^Tx + b$에 대입을 하면,

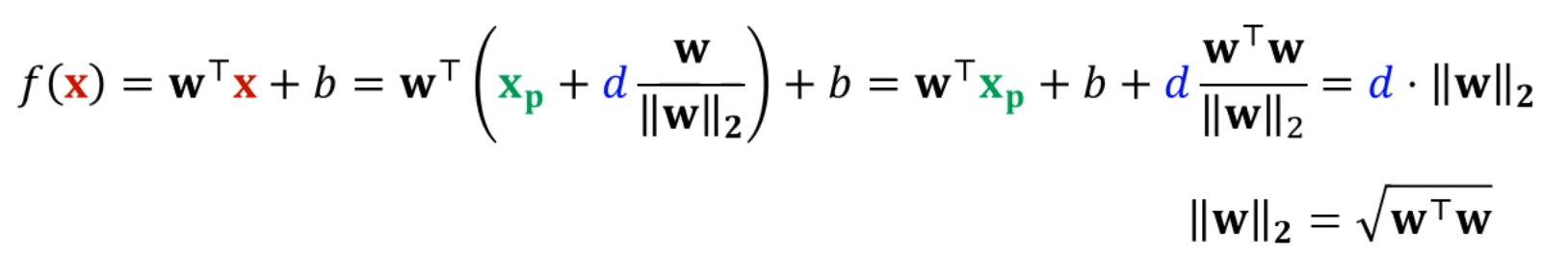
다음과 같이 정리가 되는데,
$w^Tx_p+b$는 0이죠? $x_p$는 $f(x)$ 위의 점이니까요.
그리고 $w^Tw$ = $||w||_2^2$에요.

그래서 결국 $f(x) = d||w||_2$가 남습니다.

즉!

특정 point x에서 $w^T x + b$에 내린 수선의 발의 길이는 $d = \frac{f(x)}{||w||_2}$가 됩니다.

그리고, margin을 maximize할 때,
어떤 초평면을 $w, -w$ 방향으로 늘려나가다가, 어느 점에 걸리는 순간이 늘릴 수 있는
Margin의 최대가 되겠죠?

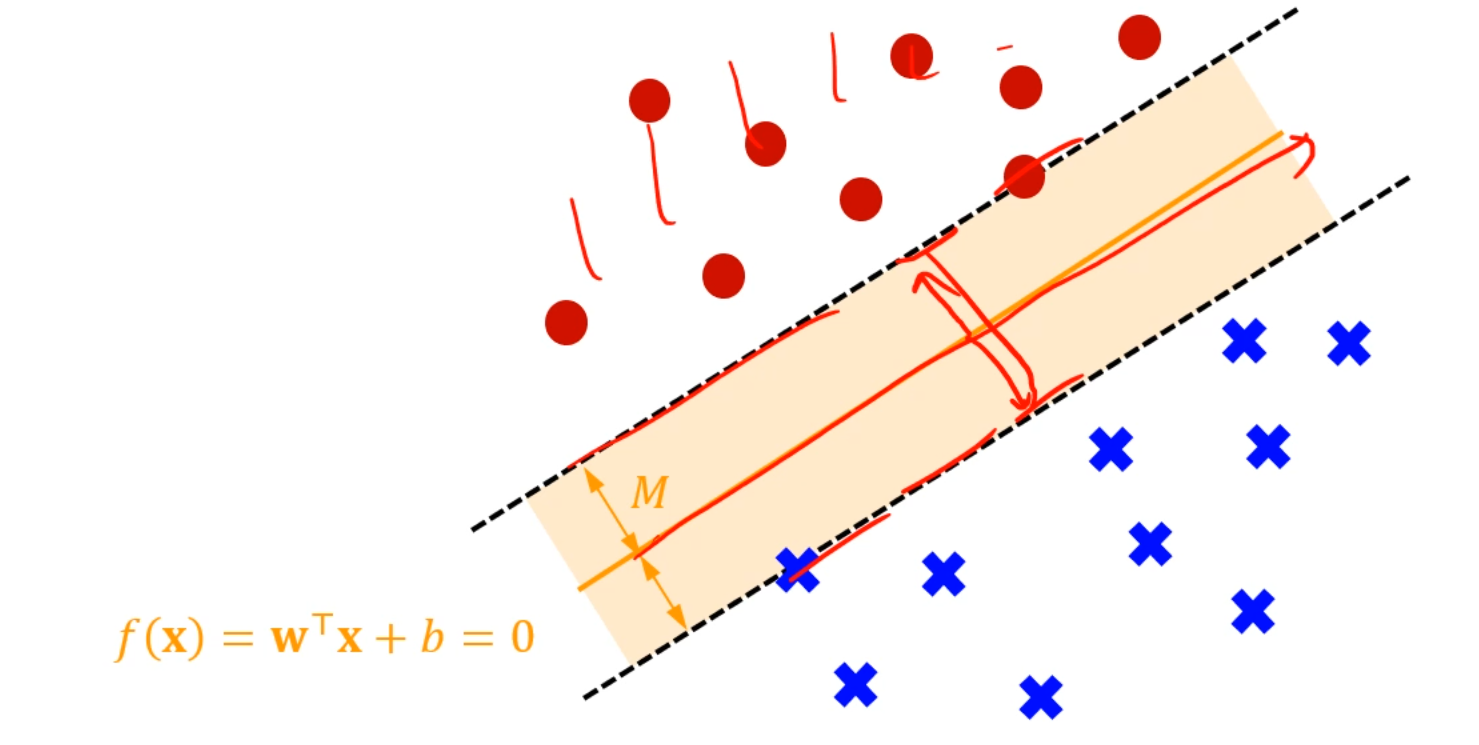
그 때 그 평행이동한 margin 선에 걸리지 않은 나머지 점들은, 전혀 영향을 미치지 않습니다.
즉, margin과 M만큼 떨어진 점들만 영향을 미칩니다.
margin이 $x_i$와 관련이 없다면, 그 $x_i$는 걍 빼버려도
w, b를 학습시키는 데에는 영향이 없죠.

이 초평면이 주어졌을 때, margin을 결정하는데 사용이 되는 저 걸리는 점들.
그 벡터들을 Support Vector라고 부릅니다.

그 Vector들은 초평면으로부터 정확히 M만큼 떨어진 벡터들이 될 것이고,
가장 초평면과 가까운, 분류하기 가장 어려운 데이터입니다.

이 Support Vector들만 마진에 영향을 미치고,
나머지는 마진에 영향을 미치지 못합니다.

초평면을 기준으로 분류할 때는, 퍼셉트론과 비슷하게
$w^Tx^{(i)}+b$가 양수냐 음수냐에 따라 분류합니다.
즉, 빨간 점은 해당 값이 양수인거고, 파란 점은 음수인거죠.

그걸 하나의 식으로 합치면,

이 됩니다. 자명하죠?

근데, 우린 margin을 maximize하고 싶잖아요?

그래서, 단순히 $x^{(i)}$가 초평면 위에 있냐 아래에 있냐를 따지지 말고,
그 '거리'가 M만큼 떨어져있는지가 궁금한겁니다.

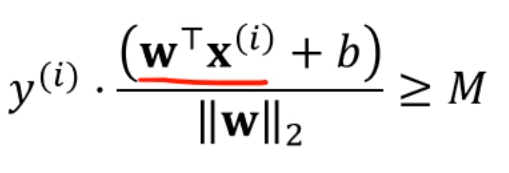
그래서, 모든 instance와 초평면 사이의 거리가 M 이상이 되기를 기대합니다.

그냥 $d \geq M$을 쓴건데, $d = \frac{f(x)}{||w||_2}$였으니까 대입을 한거죠.

Formulating a linear SVM

우리가 풀고싶은 SVM의 목적함수는 뭐냐면,

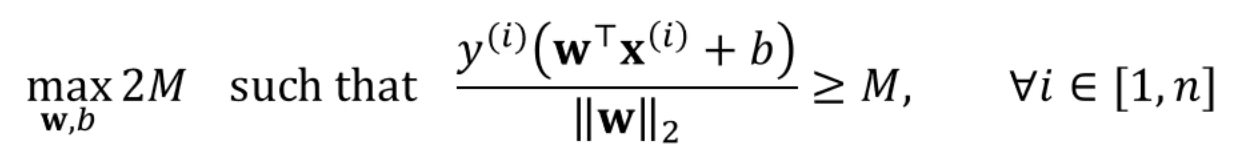
2M을 최대화하는 (margin을 최대화하는) w와 b를 구해라.
단, $\frac{y^{(i)}(w^Tx^{(i)}+b)}{||w||_2} \geq M$의 조건이 붙는다.

이걸 풀고싶은겁니다.

여기서 하나 변환을 할건데,
평면의 방정식은 상수를 곱해도 같아집니다.
$ax+by+c=0$에다가 상수 k를 곱해서, $akx+bky+ck=0$을 만든다고 변하지 않죠?
같은 의미로,
$M = 1/||w||_2$라는 조건을 임의로 추가해줄 수 있습니다.

다음과 같이 바뀌죠.
거기에, 앞선 max 2M에다가도 대입을 해주면

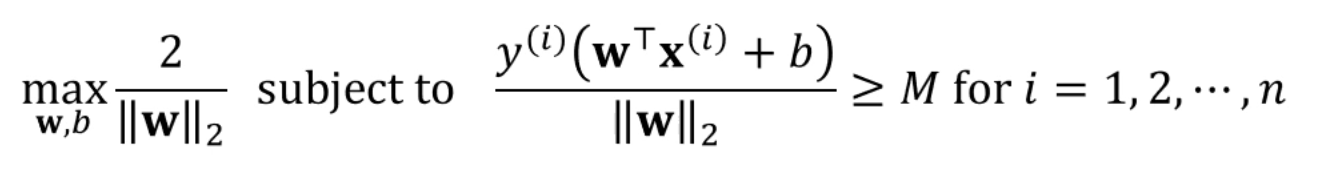
다음과 같이 바뀌는데,
$a$를 maximize하는 문제는 $\frac{1}{a}$를 minimize하는 문제와 같죠?
그리고, $\frac{1}{a}$를 minimize하는 문제는 $\frac{1}{a}^2$를 minimize하는 문제와도 같습니다.

즉, 다음과 같은 변환이 가능합니다.

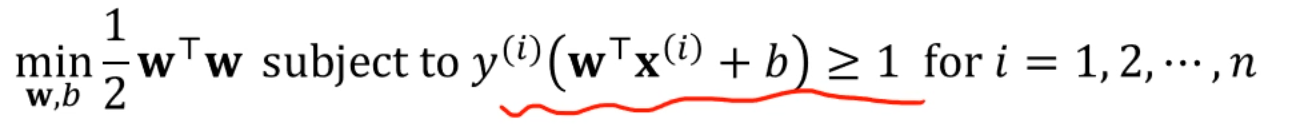
$||w||_2^2 = w^Tw$임을 이용할 수 있겠죠?

한번 손으로 학습을 해봅시다.
$\mathcal{D} = \{(1,1,-1), (2,2,+1)\}$의 데이터셋이 존재합니다.

이 데이터셋을 가지고 margin을 maximize하는 w, b를 찾아볼거에요.
그 objective function을 나타내면 다음과 같았죠?

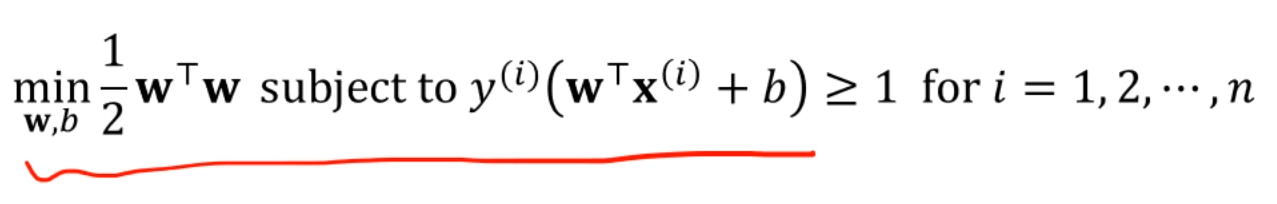
2차원 데이터셋이니까, $w = (w_1, w_2)$로 두고 각 값을 대입을 해주면,

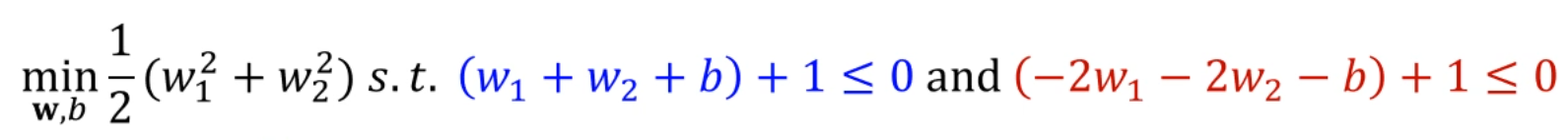
다음과 같이 대입이 되겠죠?
오, 이거 어디서 많이 본 형태 아닌가요?
라그랑주네요!

$L(w_1, w_2,b,\mu_1, \mu_2) = \frac{1}{2}(w_1^2+w_2^2)+\mu_1(w_1+w_2+b-1)+\mu_2(-2w_1-2w_2-b+1)$,
이 때 $\mu_1 \geq 0, \mu_2 \geq 0$이 성립하며,
$(w_1+w_2+b+1) \leq 0, (-2w_1-2w_2-b+1) \leq 0$ (Given condition),
$\mu_1(w_1+w_2+b-1)=0, \mu_2(-2w_1-2w_2-b+1)=0$도 성립합니다.

$w_1, w_2, b$에 대해 gradient를 구해주고, (b는 구해보면 의미가 없습니다)

$\mu_1, \mu_2$가 각각 0일 때와 아닐 때로 나눠서 이래저래 계산을 해주면,
$\mu_1 \neq 0, \mu_2 \neq 0$일 때
$w_1=1, w_2=1, b=-3$의 값이 나옵니다.

두 $\mu$가 0이 아니기 때문에, 각각의 data point에 해당하는 inequality condition이 activate되었다는 뜻이고,
두 data point들이 둘 다 support vector라는 뜻입니다.

Non-linearly separable data

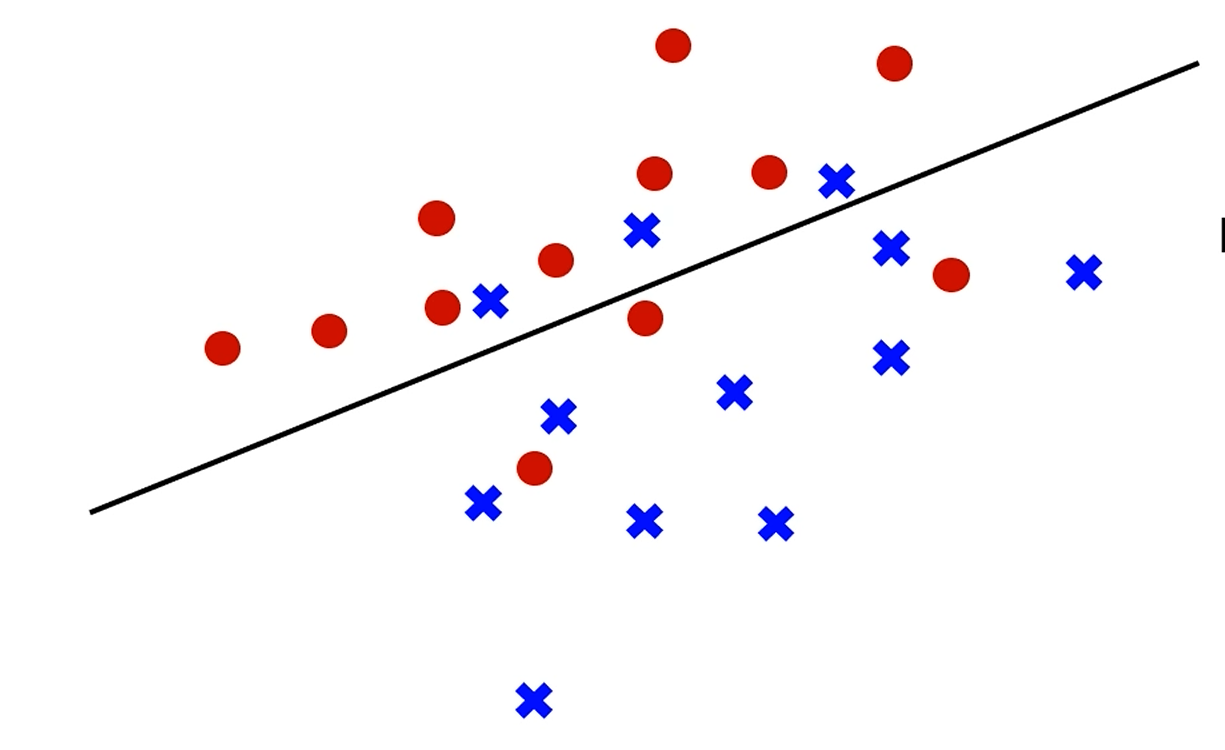
엥?
이렇게 선형적으로 나눌 수 없으면 어떻게 됩니까?
기존의 방법을 적용하면 해가 안 나옵니다.

여기서, 몇 가지 sample은 margin보다 안 쪽에 있던가, 아예 반대편에 있더라도
관대하게 봐줍니다.

지금까지 배운 SVM을 Hard Margin SVM이라고 부릅니다.
모든 점은 boundary에 대해 Margin 이상으로 떨어져 있어야 합니다.

지금부터 배울 SVM은 Soft Margin SVM이라고 부릅니다.

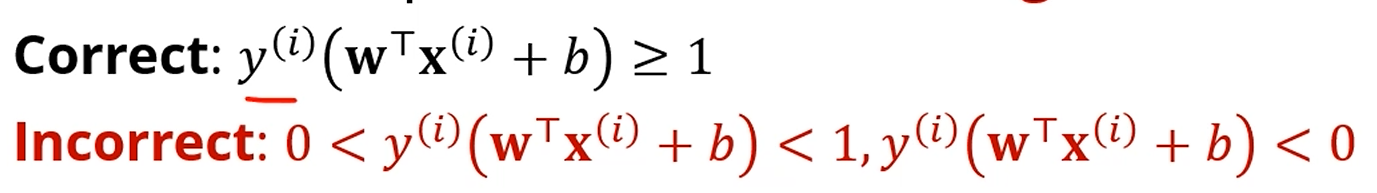
원래는 inequality condition이 만족되는데,
이제는 1보다 작던가, 심지어 음수가 나와도 (오분류) 이해를 해주려 합니다.

그리고, 얼마나 틀렸는지를 알기 위해 $\xi_i$로 표현합니다.

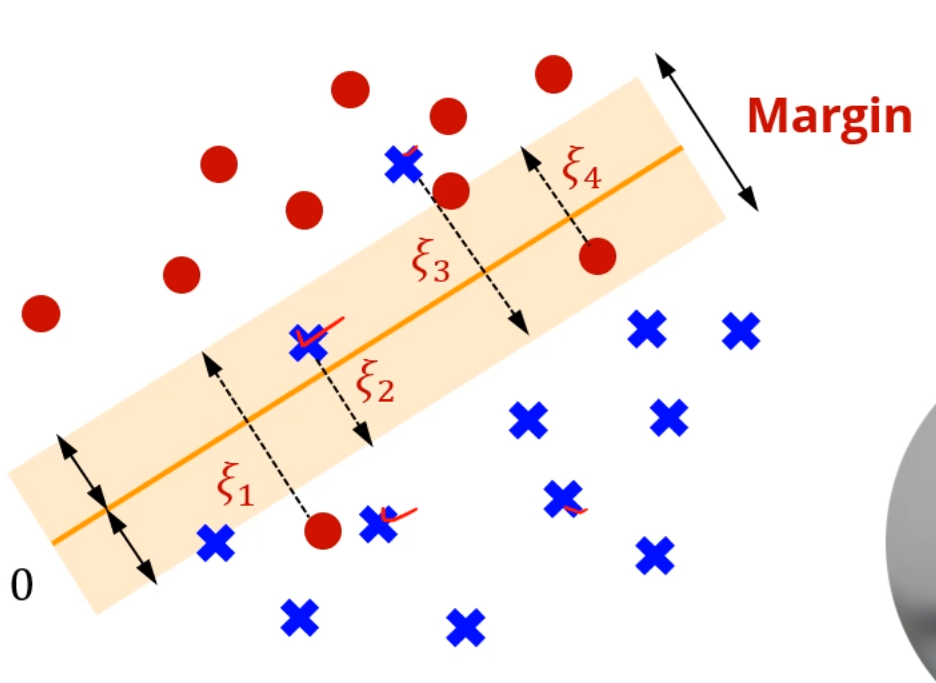
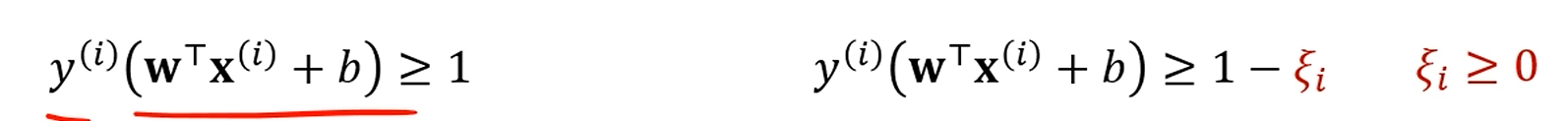
이제는, $1 - \xi_i$보다만 그 값이 크면 적당히 봐주기로 한겁니다.

대신, 역시 오차는 오차니까 원래 objective function에 $\sum_i\xi_i$만큼의 penalty를 줍니다.

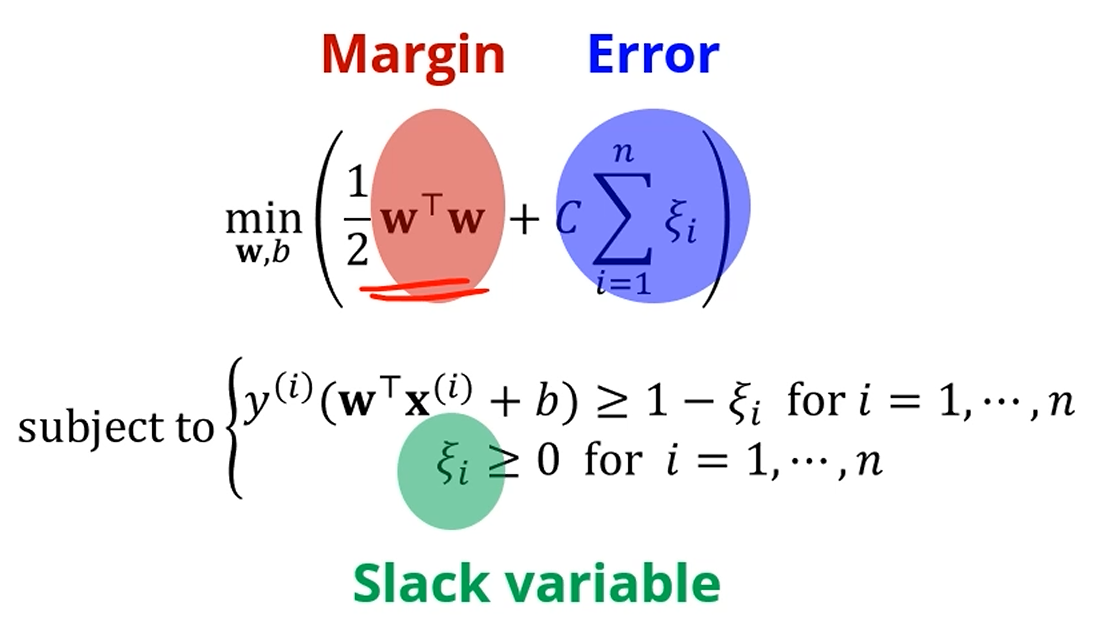
이제 Margin과 관련된 값에, Error까지 포함한 저 값까지 줄이자.

근데, Margin을 늘리는걸 중요하게 여길지,
Error를 줄이는걸 더 중요히 여길지는 중간에 껴있는 C가 결정합니다.

또한, subject function에 $\xi$도 집어넣습니다.

아이고. 딱봐도 할게 많네요.

C가 클수록 error를 허용하지 않고, (overfitting)
C가 작을수록 그냥 margin을 최대화하는데에만 신경을 씁니다. (Over-generalization)

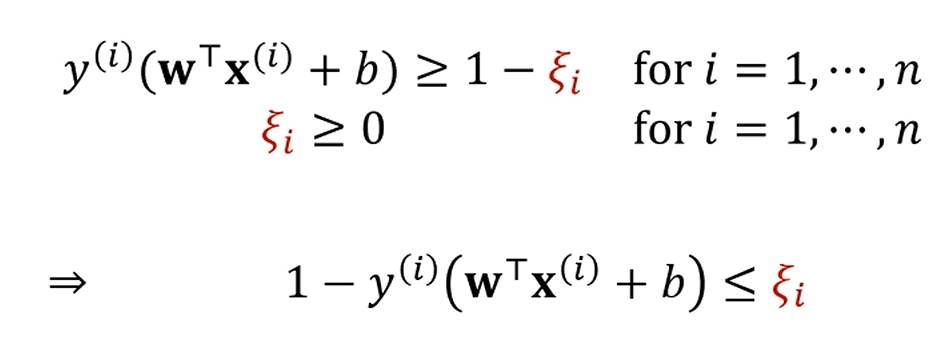
이 두가지 subject function을 섞을 수 있습니다.

좌항이 음수라면, $\xi_i$의 최솟값은 0입니다.
좌항이 양수라면, $\xi_i$의 최솟값은 글자 그대로의 $1-y^i(w^Tx^i+b)$가 되구요.

즉,

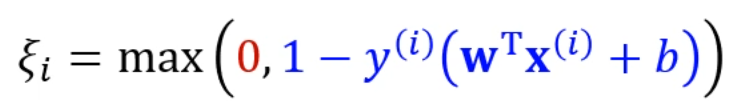
$\xi_i$는 날고 기어봤자 0 또는 저 값 중 하나가 됩니다.
그럼 slack penalty도 조정 가능합니다.

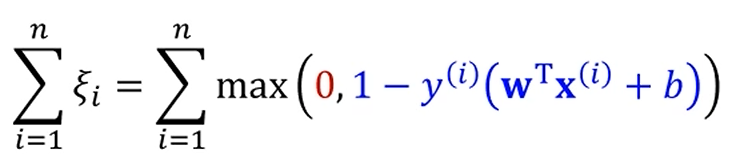
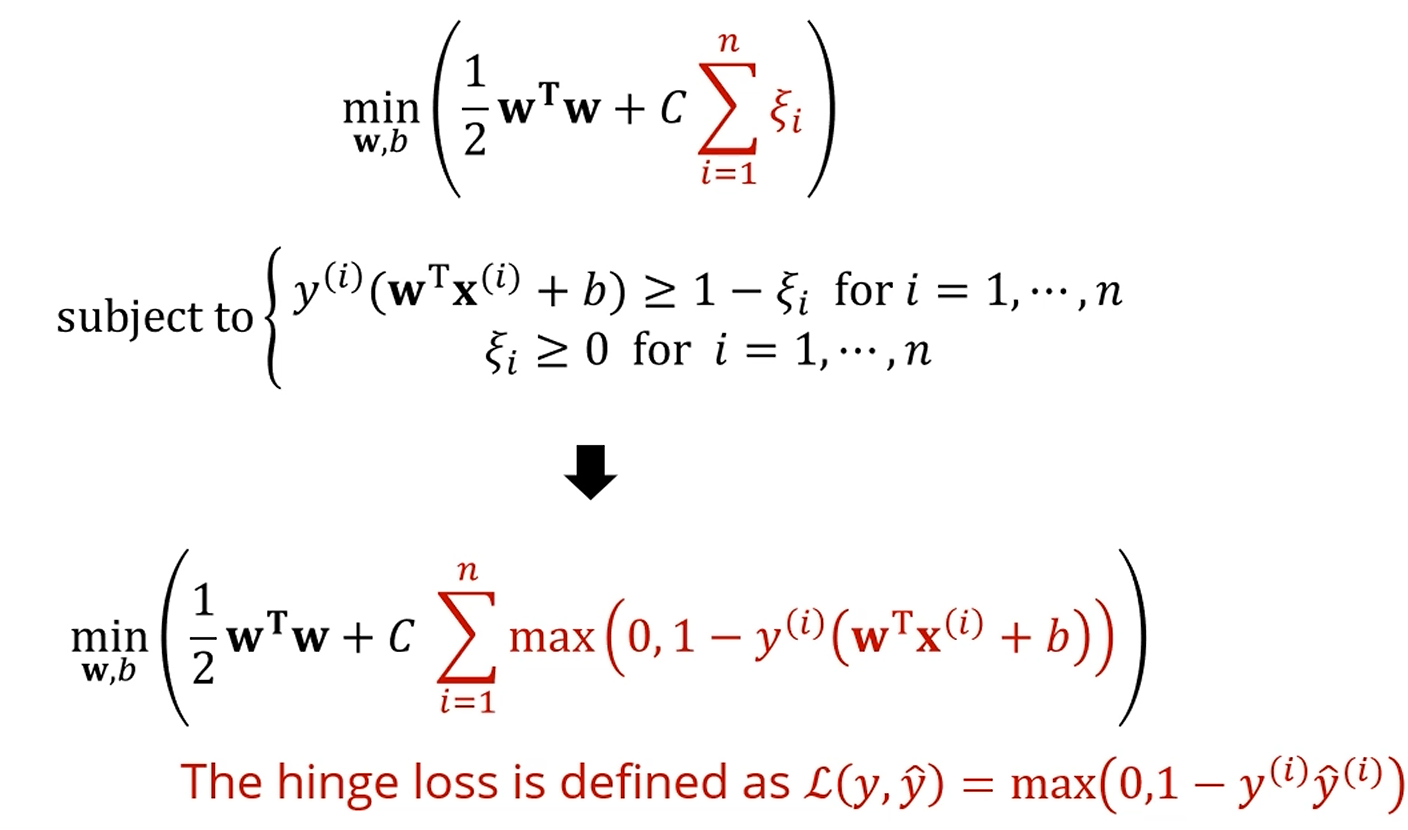
이렇게 치환함으로서, 위에 있는 subject function을 $max$로 바꿔버렸습니다.
이제는 가장 밑의 식만 풀면 돼요.

그리고 뒤쪽의, slack 최소화하던 부분을 hinge loss라고 부릅니다.

아래는 SVM 문제를 바라보는 또 다른 방향입니다.

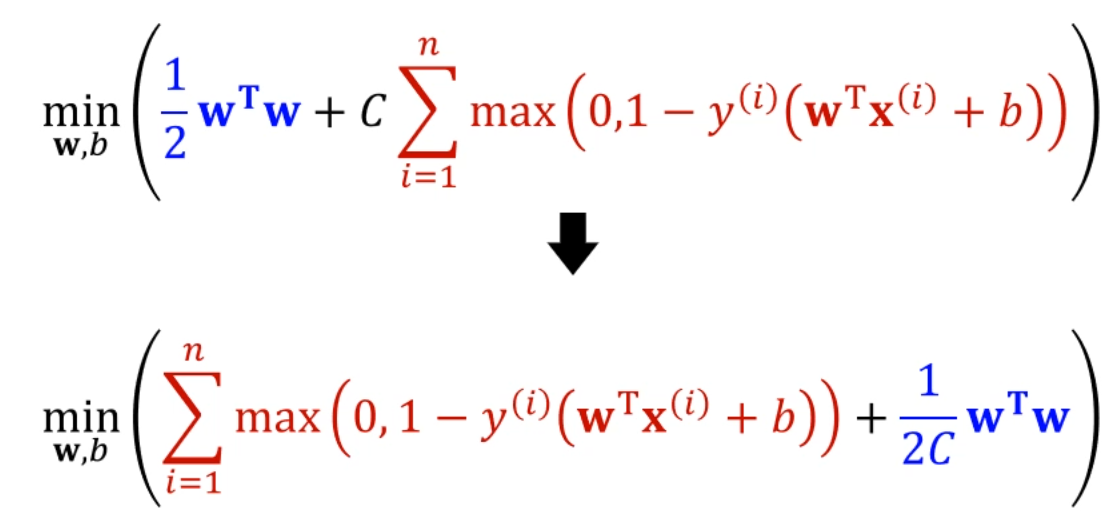
앞선 hinge loss는 그냥 '학습 데이터에 대한 hinge loss의 합'이 되는거고,
두번째 항은 따지고보면 $\lambda ||w||_2^2$를 줄이는 문제네요?
$w$의 L2 regularization을 추가한 문제네요?

세상에.

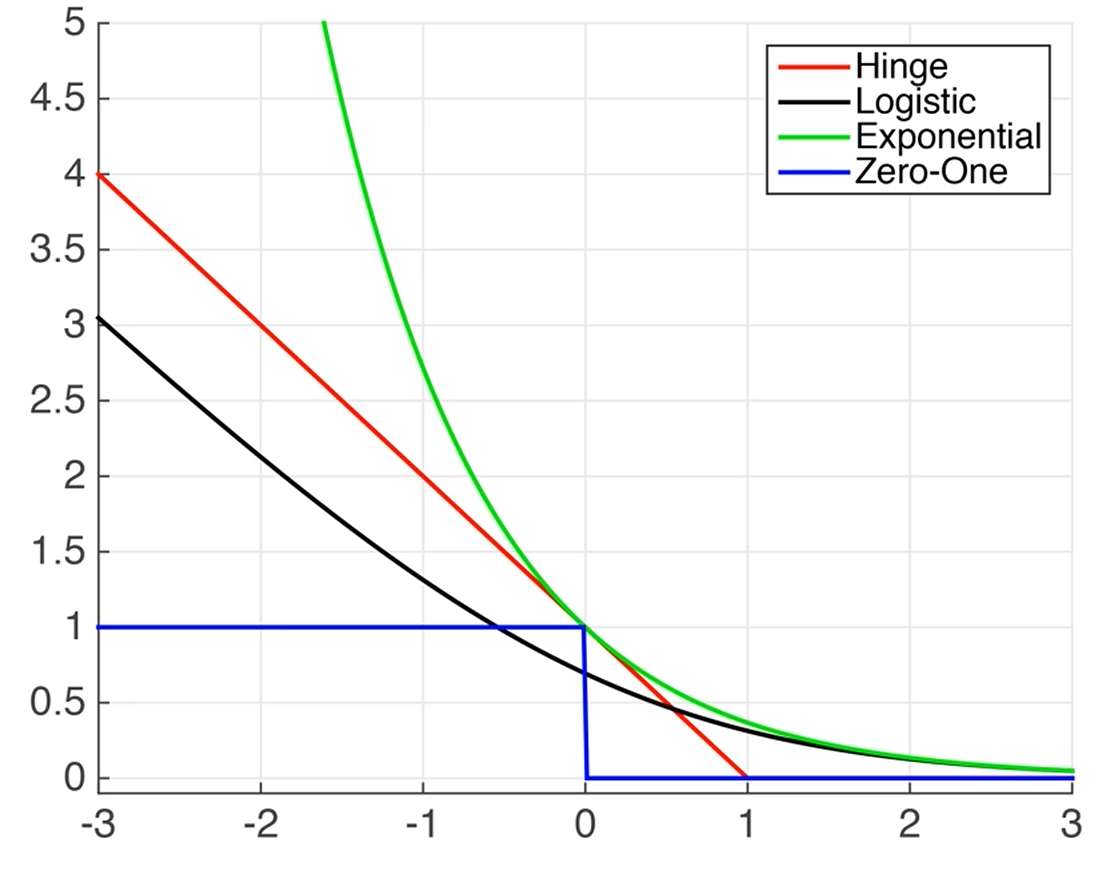
Hinge loss는 0/1 loss, 양수면 0이고 음수면 1인 저 step function의
upper bound 역할을 하게 됩니다.