Variance of Bagging
Bagging의 분산을 얘기할 때, 다음과 같이 얘기했습니다.
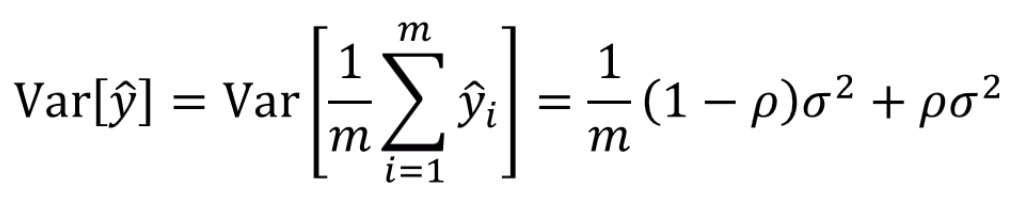
갑자기 는 어디서 튀어나온거고, 왜 가 저렇게 튀어나오는지 확인을 해봅시다.
하나 기억할 내용은, 이어도 X,Y가 꼭 독립은 아니라는 것,
하지만 그 역은 성립한다는 것 정도입니다.
우선, Correlation 를 구하는 식은 다음과 같습니다.
이라면 X,Y 사이에 선형관계가, 이라면 X,Y 사이에 negative 선형관계가 성립함을 의미합니다.
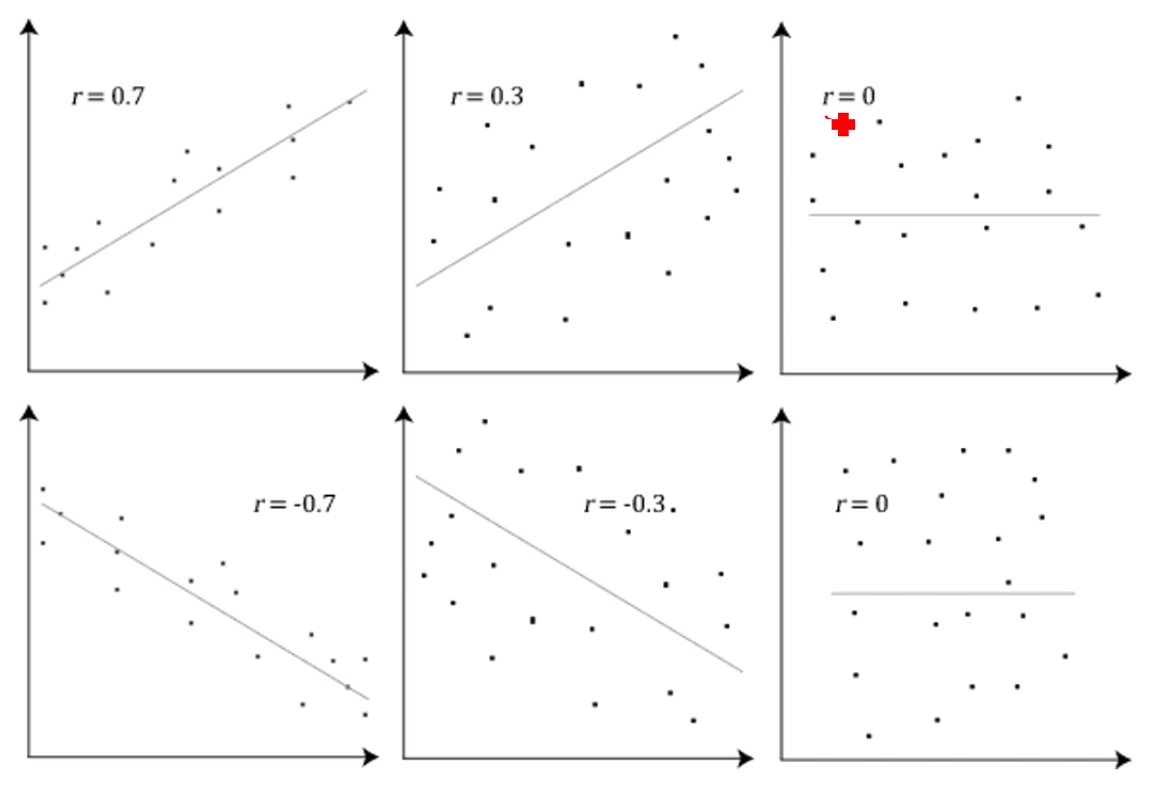
그리고 이면 딱히 선형 상관관계를 찾을 수가 없다 정도로 이해하면 될 것 같습니다.
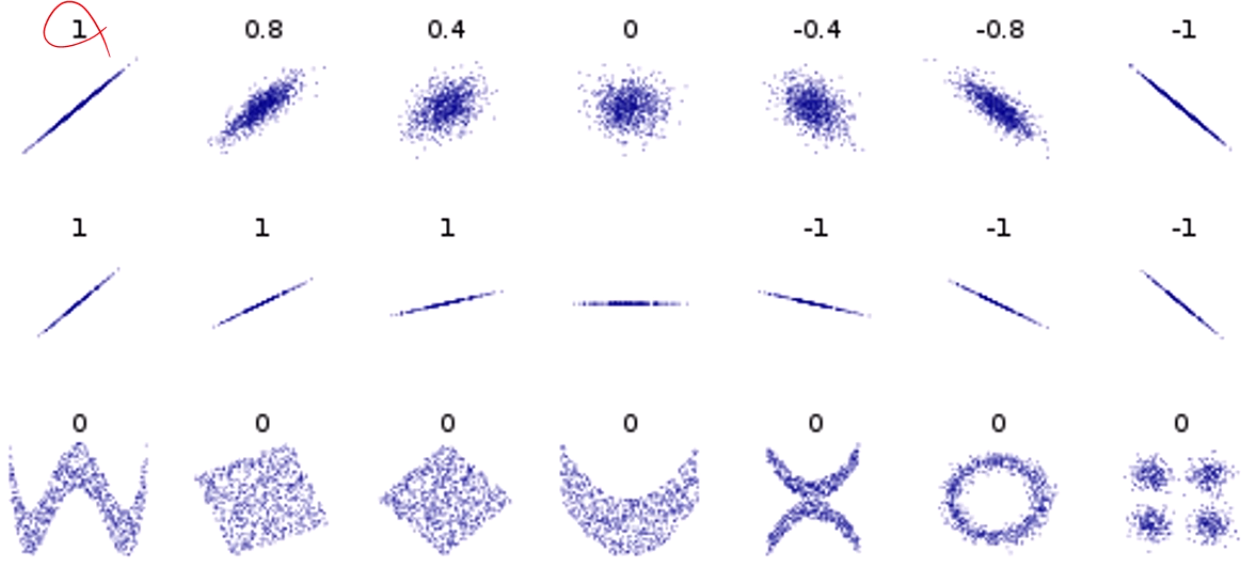
에 따른 분포의 차이입니다.
중요한건, 인 경우에 (Cov가 0인 경우) 꼭 X,Y가 독립이라는건 틀린 명제이고,
연관이 있긴 한데 선형적인 연관은 없다 정도로 보면 됩니다.
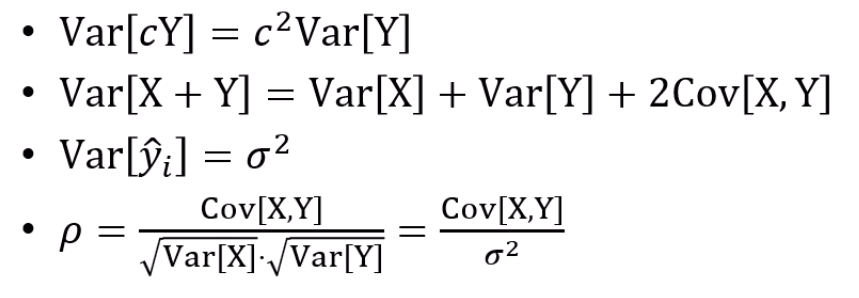
이 내용들을 숙지하고, 한번 유도를 해봅시다.
우리가 보이고자하는 내용은
입니다.
는 자명하죠?
각 모델들의 출력의 평균을 로 정의했으니까요.
이고,
를 풀어 쓰면
이구요,
를 감안하여
전부 전개를 해주면,
이 나오고,
이렇게 쭉 나옵니다.
결국 이 나오고, 에 의해 가 개 생성됩니다.
이쁘게 쓰면
가 되고,
정리하면
가 되고,
이걸 정리해주면
가 완성됩니다.
Bagging의 Variance 유도 성공!
Derivation of and in AdaBoost
다음 loss function을 가정해봅시다.
물론 이진분류 문제용 Loss function입니다.
정분류 되었다면 loss는 작고, 오분류 되었다면 loss는 크겠죠.
그 중에서도 답이 1일 때 분류를 3으로 했다면 Loss가 더 작고,
답이 1일 때 분류를 1로 했다면 그것보단 Loss가 커집니다.
Weak Classifier를 k개 만들었다고 해봅시다.
그리고 그 classifier들의 weight (투표권)을
로 둡니다.
m-1번의 iteration을 돌고 났을 때, 그것들을 다 합친 최종 모델은 다음과 같습니다.
여기에 새 classifier를 얹어서 다시 ensemble을 해봅시다.
그 새 Classifier의 loss는 어떻게 계산이 될까요?
가 되겠죠?
각 query point i에 대한 loss를 다 더한 값이 총 Error일테니까요.
형태를 해석하면 번째 classifier 이전의 loss와, 번째 classifier의 error가 곱해지는 형태가 되네요.
AdaBoost에선 sample마다 weight가 존재했습니다.
오분류 시 weight가 증가하여 다음 classifier에게 넘어갔죠.
그 때 말했던 i번째 sample에 대한 weight, 즉 이 가 됩니다.
m-1번째 classifier까지 다 더해서 만들어진 i번째 sample의 loss에 대한 정보가
m번째 classifier의 i번째 원소의 weight로 반영이 될테니까요.
그러면 m번째 classifier의 error는
이 되죠.
m번째 classifier를 만들 때,
이전까지 만든 weak learner들의 ensemble과
방금 만든 classifier를 합쳤을 때의 전체 손실에 대한 식이 E입니다.
여기서 수학적인 부분이 들어옵니다.
지금 학습중인 m번째 weak learner가 맞췄는지 틀렸는지 알바 없고,
그냥 모든 sample에 대해 weight와 현재 weak learner의 error까지 곱해서 계산이 되는건데,
그걸 맞춘 샘플과 못맞춘 샘플로 쪼개봅시다.
전항의 경우, 맞췄으니까 만 남고, 후항의 경우 못맞췄으니 부호가 뒤집힙니다.
아직까지는 직관적인 전개입니다.
목표는 Error를 최소화하는 을 찾는 것입니다.
보통 최소화를 하면 미분을 떠올리죠.
우리가
를 최소화하는 x를 찾고 싶을 때, 미분하여 0을 만듭니다.
그러면
에서 최소가 됩니다.
이걸 왜 하냐구요?
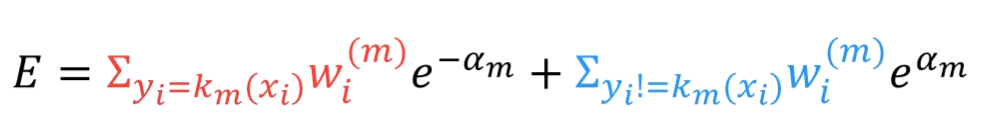
이 식을 로 해석을 하면, ()
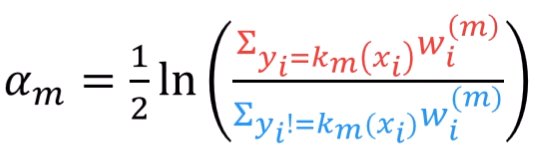
다음 상황에서 최소화가 됩니다.
우리가, m번째 classifier가 만들어내는 error의 총합을,
이라고 두고,
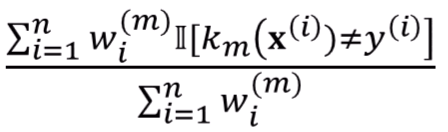
다음과 같이 정의합니다.
각 weak learner k가 오분류한 샘플에 대해 weight를 부여하여 loss를 정의하는거죠.
분모는 정규화를 위해 넣은거구요.
이 값을 이용하면,
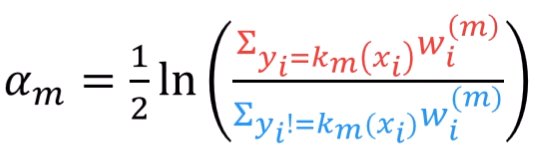
이 값이 해석이 되죠. 분모 (파란색)은 과 정확히 일치하구요, (정규화 부분 빼고)
분자 (빨간색)은 이라고 적을 수 있습니다.
Manifold
재밌는 내용을 배워봅시다!
일반적으로, ML 모델에서 차원이라고 하면 데이터에 존재하는 Attribute의 개수입니다.
[키, 몸무게]를 받아서 [재산]을 예측한다면, (말은 안되지만,)
2차원 데이터를 받은 것과 같아집니다.
[키, 몸무게, 시력]을 받았다면 3차원 데이터를 받은거구요.
근데, 일반적으로 ML 모델에선 입력 데이터가 훨씬 고차원입니다.

다음과 같은 MNIST Dataset을 보면, 이미지 하나가 data instance 하나인데,
28 * 28 pixel로 이뤄져 있습니다.
하나의 pixel은 0 or 1 (흑 or 백)입니다.
저 이미지 1장은 0 또는 1이 28*28 = 784개의 데이터 (784차원)으로 표현됩니다.
말이 안되죠? 엄청 커요.
각 차원이 0 또는 1인데, 그 차원을 꽉 채워서 표현하려면 개의 샘플이 필요합니다.
근데, MNIST dataset은 7만개밖에 없고,
우리는 의 엄청난 큰 차원을 7만개의 샘플만으로 이해해야 합니다.

쪼만한 5*5짜리 MNIST를 가정해봅시다.
이 데이터는 1로 분류되겠네요.
다행히도, 이 경우에는 개의 데이터만 있으면 전체 데이터를 표현할 수 있습니다.
분류율 100%를 채울 수 있겠죠.
근데, 진짜 3200만개 데이터가 필요할까요?

이런애들은 의미가 없습니다. 이론적으로는 공간상으로 의미가 있지만,
실제로는 손글씨가 아니죠. 아무 의미가 없습니다.
이런 case까지 다 고려하고 싶다면 25차원이 다 필요한데,
현실적으로 실제로 관측되기 어려운 데이터들은 noise이기 때문에,
어느정도는 쳐낼 수 있어요.
실제로 수집된 데이터들이 100차원으로 표현이 되어도,
그 100차원이 전부 다 알차게 사용되진 않으리라는 추측을 할 수 있습니다.
데이터의 특성에 따라서 실제로는 관찰하지 못할 점들도 표현이 될 수 있으니까요.
우린 어떤 축으로 데이터가 distribute되는지 아직은 모릅니다.
하지만, 총 25개의 차원 모두가 필요한건 아니라는건 알고 있죠.

우리는 제일 왼쪽 이미지로부터, 딱 1개의 픽셀만 바꾼 25개의 이웃을 생각할 수 있는데,
그 25개의 이웃들이 모두 유효하냐? 그럼 그건 아니죠.
가령 제일 오른쪽 이미지는 실제 손글씨 dataset에 존재하지 않을겁니다.
그 어떤 손글씨도 나타내고 있지 않잖아요.
어떤 dataset이 존재하는 굉장한 고차원에서,
모든 차원이 다 알차게 사용되는게 아니라,
어떤 점마다 지역적으로는 훨씬 적은 차원으로도 관계를 표시할 수 있다 -
이런 가정을 해볼 수 있습니다.
(실제로 그런지는 우리는 모릅니다. 하지만 가정까지는 가능합니다.)
우리가 수집한 데이터는 굉장히 고차원이지만,
의미가 있는 실제로 관찰된 데이터들이 이루고 있는 구조는
지역적으로는 저차원일 것이다.
이러한 가정을 Manifold Hypothesis라고 부릅니다.
그 저차원 구조를 Manifold라고 부르구요.

흑백 이미지에 도형이 그려졌습니다.
이미지가 32*32 pixel이기에 실제로는 1024차원입니다.
실제로는 개의 가짓수를 가질 수 있겠죠.
이 그림들을 어떤 차원으로 나타낼 수 있을까요?
Shape (원, 사각형, 하트),
Size,
Orientation,
PosX,
PosY 정도가 존재할겁니다.
(더 있을수도 있죠!)
우리는 1024차원을 5차원으로 줄일 수 있게 되었습니다.
pixel space에서 표현하면 1024차원이지만, 압축 space에서 표현하면 5차원인거죠.
이런 dimension을, 실제로 의미있는 정보를 담은 차원을 Hidden Dimension이라고 부르구요.
대부분의 경우는 Hidden Dimension이 더 좋습니다.
당연히 데이터가 압축이 되어서 좋구요,
독립입니다.
차원 간의 연관성이 사라져요.
보통 pixel space에서는 그림을 그리면 연속적으로 그리기 때문에,
하나의 pixel이 1이면 인접한 pixel이 1일 확률이 높아집니다.
근데, PosX나 Orientation같은 차원들은 딱 봐도 독립이죠.
또, Meaningful합니다.
Pixel을 그대로 보는 것 보다, 5개로 압축해서 보면 5개의 의미가 해석이 되죠.
Data에 대한 Insight를 얻습니다.
또 Noise에 더 robust합니다.
Terminology
우리가 관찰한 1024차원을 Observed Dimension이라 부르고,
내재될 것이라고 예측되는 5차원을 Latent Dimension이라고 칭합니다.
그리고 그런 Latent Dimension에 의해 만들어진 공간을
Latent Space라고 칭합니다.
또, 특정한 경우에는 그런 Latent Dimension끼리 독립이기를 기대합니다.
그래서, Latent Dimension들이 독립이 되게 풀어헤치는 작업을
Disentangling the representations라고 표현합니다.
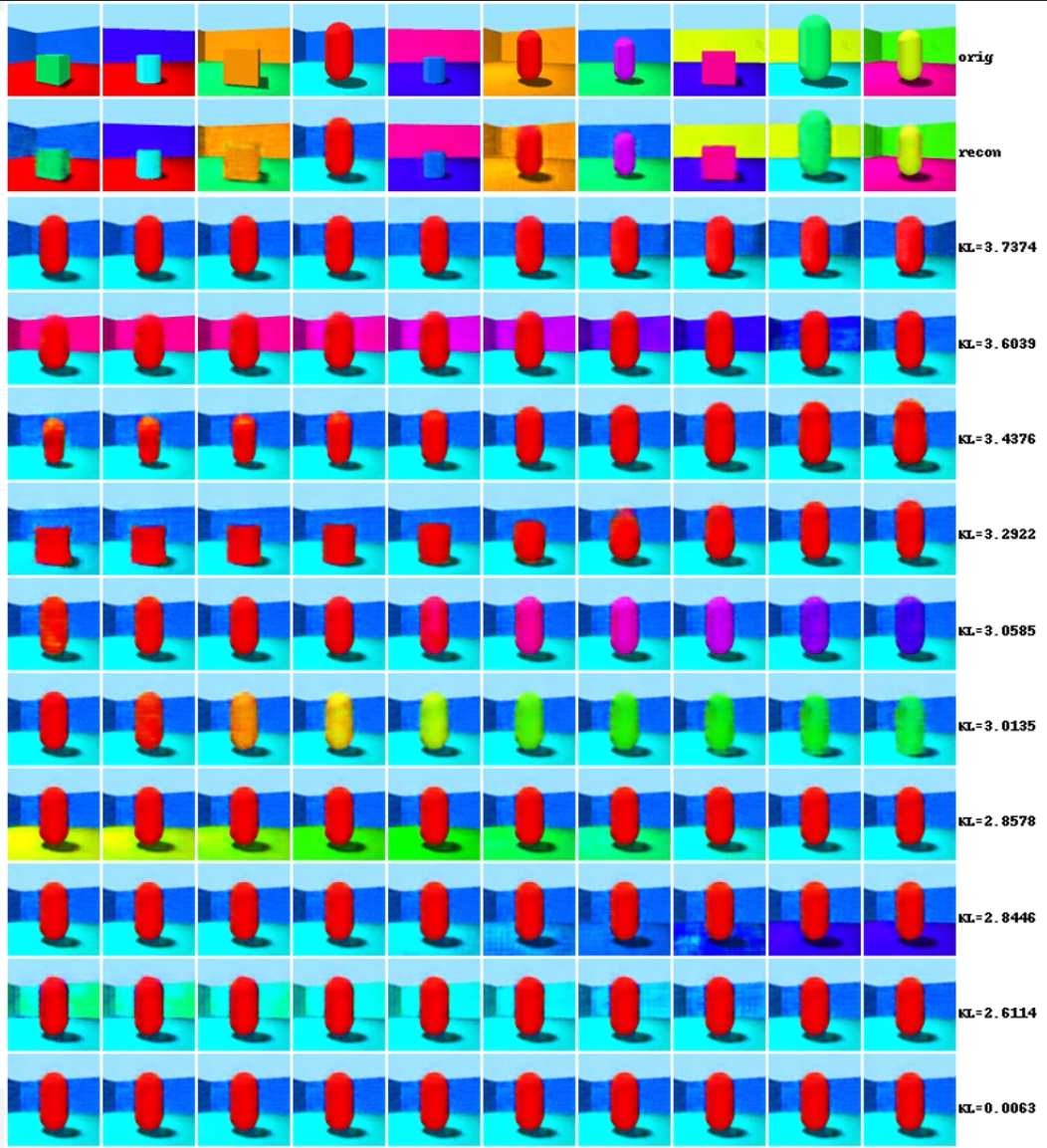
하나의 세로줄이 하나의 차원입니다.
Disentangling이 잘 되었다면, 하나의 차원의 값을 바꾸면 해당하는 값 하나만 살짝 바뀌어야 겠죠.
4번째 차원은 뒤쪽 배경의 RGB차원일 거고,
6번째 차원은 '얼마나 정사각형이냐' 를 나타내는 차원일것 같네요.
차원의 값을 바꿀 때, 관찰된 결과의 '하나의 차원'만 값이 바뀌기를 기대하는 것입니다.
(물론 Disentangling이 항상 목표는 아니에요)
우리가 모델을 만들어서,
그 모델이 관측된 고차원에서 중요한 정보를 뽑아서,
저차원의 Latent Space에 매핑하는 모델을 만든다면,
그 모델을 Encoder라고 부릅니다.
Encoding을 통해서 입력 데이터를 우리가 아는 유용한 차원의 벡터로 바꾸는거죠.
저차원 상에서는 훨씬 밀도가 당연히 훨씬 높아지겠죠.
784차원을 5차원으로 내리면 밀도가 dense해지죠.
그렇게 만들어진 밀도가 빡빡한 표현을 embedding이라고 부릅니다.
그래서,
고차원 데이터셋이, 실제 세상에서 훨씬 작은 숫자의 잠재된 latent space로 표현될 것이라는 가정이 manifold hypothesis이며,
그 low-dimensional 구조를 manifold라고 칭합니다.
(한번 더 나왔네요.)
Swiss Roll Dataset
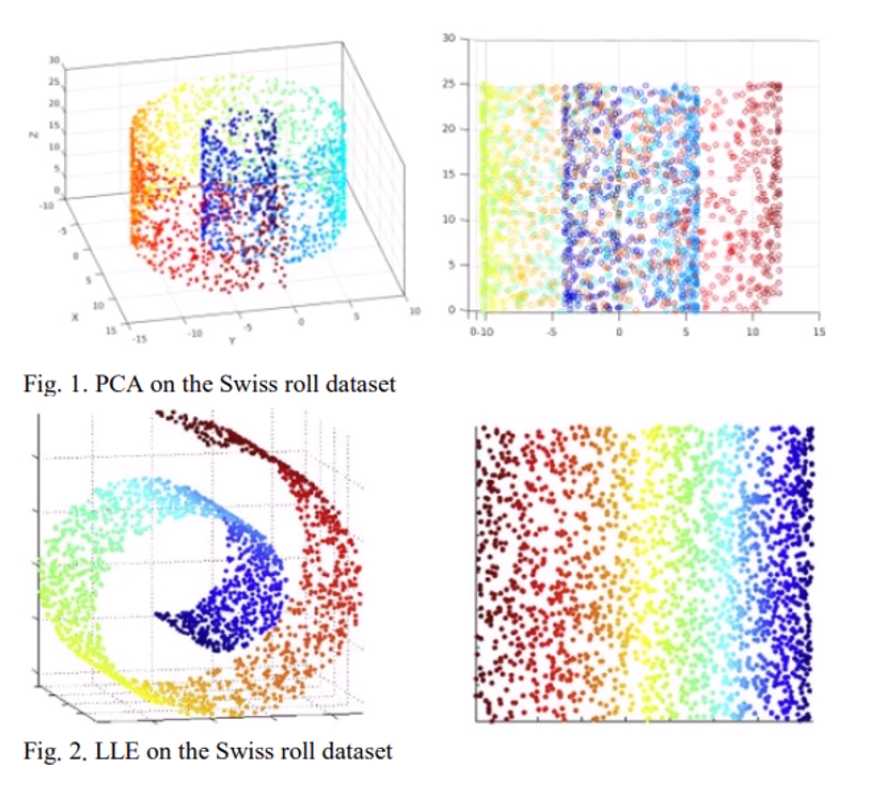
이 누가 봐도 3차원인 데이터가 있습니다.
우리가 이 데이터를 나타낼 때, 점들 사이의 관계가 얼마나 중요한가요?
한번에 보는 우리 입장에서야 '너희는 3차원에서 꼬여있다' 라고 하는거지,
지역적으로 볼 땐 2차원인 구조입니다.
'3차원 세계에 사는 2차원 데이터셋' 이라고 볼 수 있구요.
그걸 이런저런 알고리즘으로 풀어헤치면, 오른쪽 사진처럼 나타납니다.
물론, 그러면 정보의 손실이 좀 일어나긴 합니다.
왼쪽 swiss roll에서 '나와 조금 멀리 떨어진 애들간의 거리관계' 같은 경우는
좀 왜곡이 됩니다.
하지만, 보통의 경우에는 고차원 데이터셋에서 인접하지 않은 애들은 별로 의미가 없기에,
그런 것들은 희생을 시키고 저차원으로 내릴 수 있지요.
Manifold Examples
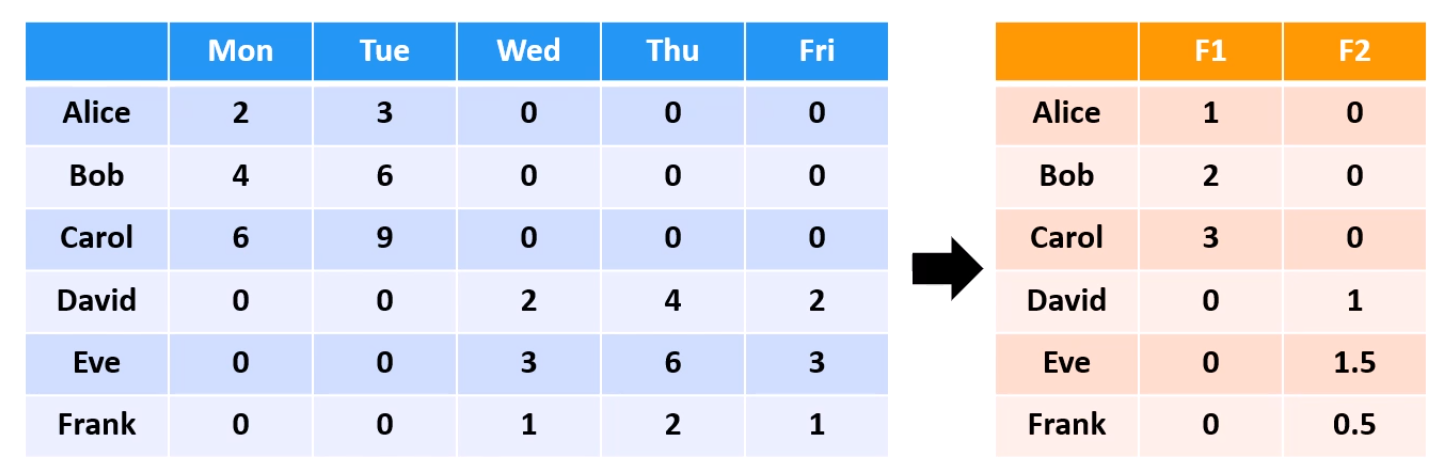
이런 데이터셋은 5차원 데이터셋이죠. dimension이 5개니까요.
근데 자세히 보면 Mon, Tue는 굉장히 큰 연관관계가 있고,
Wed, Thu, Fri도 관계가 매우 밀접합니다.
그래서, 그걸 좀 들여다 보면, 알고 보면 2차원 이라는 걸 알 수 있고,
차원축소가 가능해집니다.
5차원 세상에 2차원 데이터셋이 살고 있었네요.
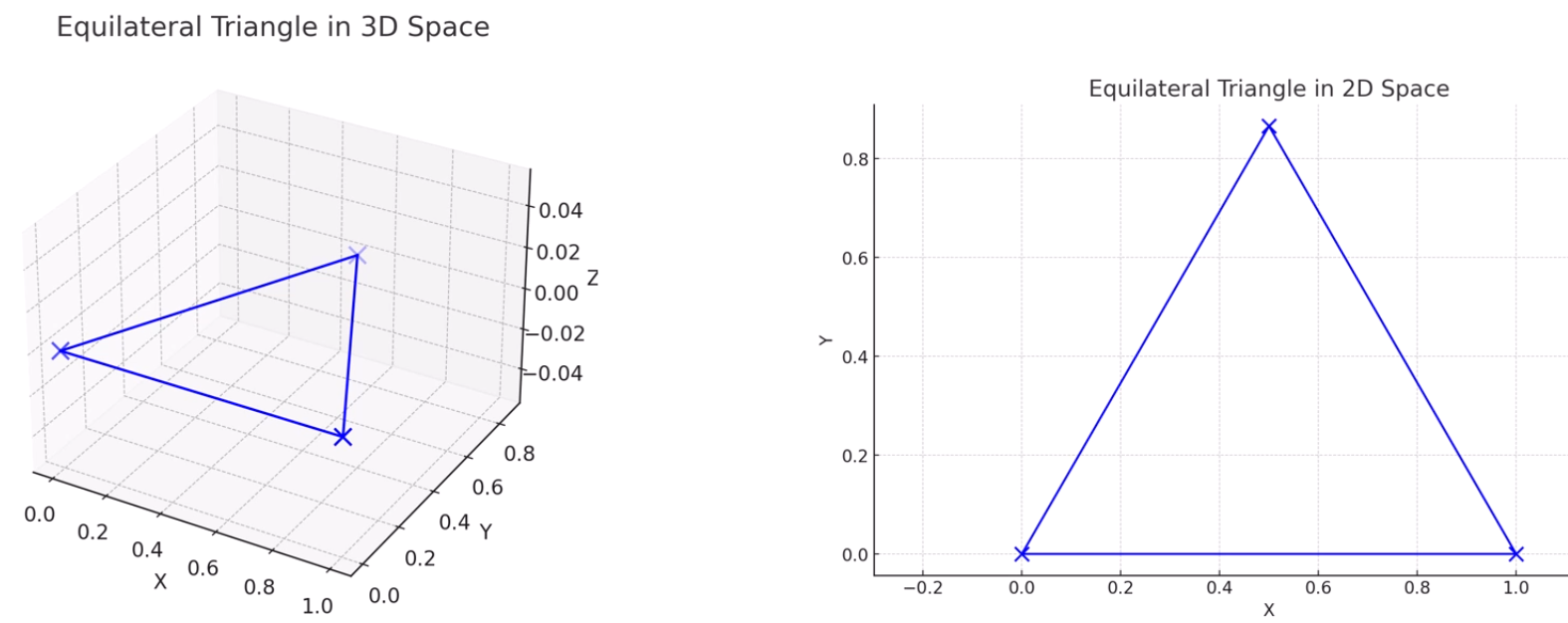
3차원 삼각형을 정보손실 없이 2차원으로 내릴 수 있습니다.
점과 점 사이의 관계가 전혀 왜곡되지 않았네요.
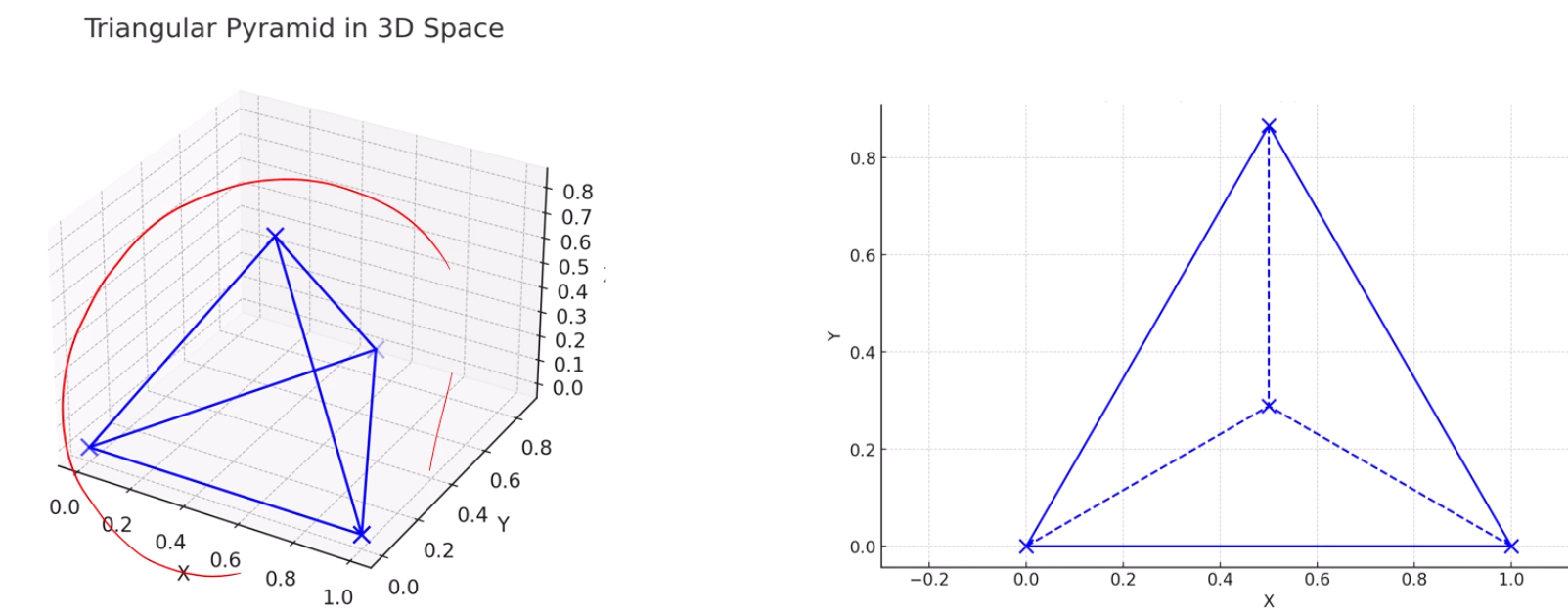
물론, 이런 경우에는 어쩔 수 없이 정보손실이 일어나네요.
분명 다 같은 길이인데, 2차원 상에서는 어쩔수 없이 점선의 길이가 왜곡됩니다.
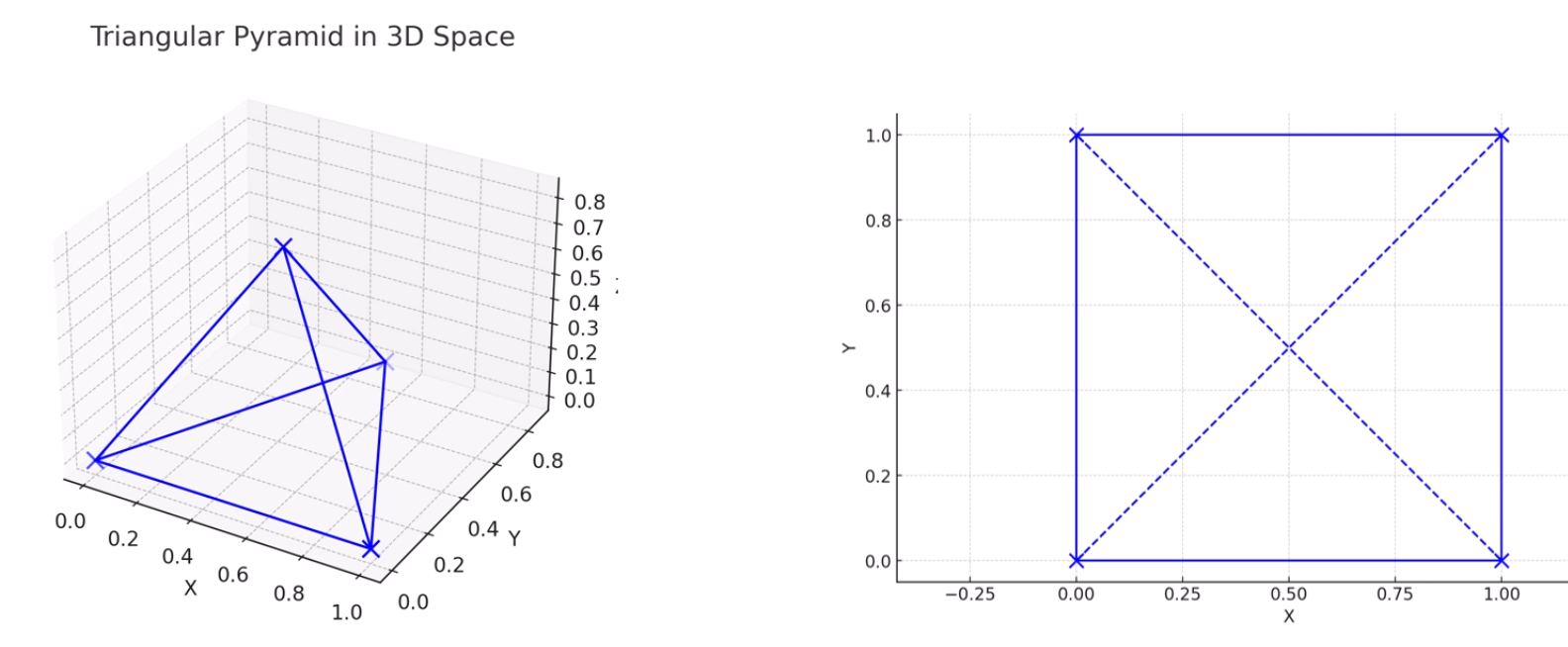
이렇게 표현하면요?
4개의 변을 지켰네요. 근데 2개의 변이 거리가 좀 많이 왜곡되네요.
똑같이 차원축소를 했지만, quality가 좀 가변적이네요.
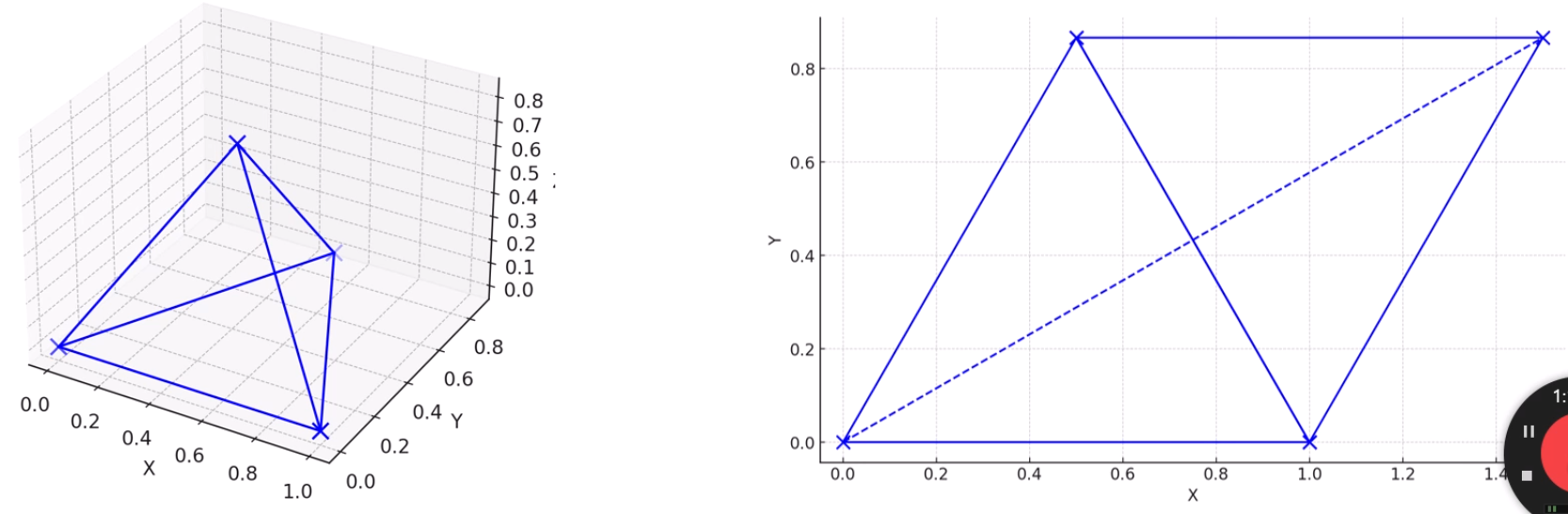
이렇게 나타내면 5개를 잘 유지하지만, 나머지 1개가 매우 왜곡됩니다.
