Neural Net and Backpropagation

햄스터·2024년 12월 14일

FOML

목록 보기

5/12

Neurons

사람의 뇌에 있는게 뉴런이죠.
뉴런은 특정 threshold를 넘는 전기자극이 들어오면, synapse를 통해
다른 Neuron에 전기 자극을 쏩니다.

우린 거기서 영감을 얻었습니다.

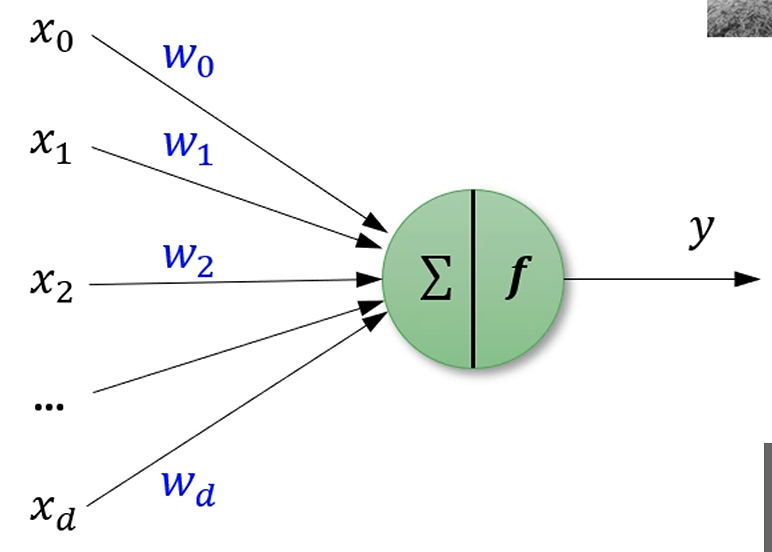
여러 Neuron에게서 쭉 자극을 받습니다. ( $x_0, x_1, ... x_d$ )
학습 가능한 가중치도 곱해서요.
그걸 다 선형합을 구해서, 특정 threshold보다 높다면, 다른 neuron에 fire 해줍니다.
이런 구조를 Perceptron이라고 불러요.

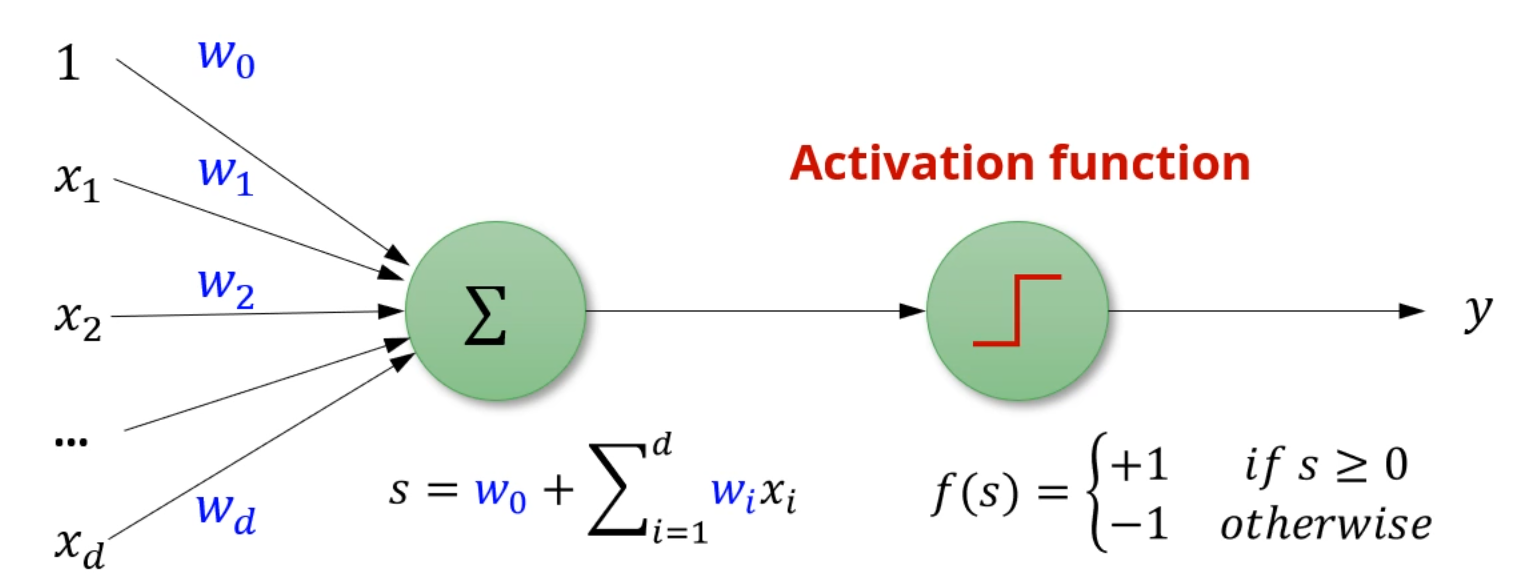
좀 더 구체적인 식으로는,
절편을 유연히 처리하기 위한 $x_0 = 1$ 를 포함하여, 여러 neuron으로부터 온 입력에
가중치를 곱하여 처리를 해줍니다.

s = w_0 + \sum_{i=1}^d w_ix_i

여기에 activation function $f$ 를 적용하여, 여기선 threshold 0을 넘으면 fire하네요.

이렇게 활성화 함수를 거치는걸 비선형적 변형을 한다고 표현하기도 합니다.

이 모델을 가지고 이진분류기를 만들어봅시다.

$f(x) = w^Tx$ 가 $\geq0$ 이면 +1로, $\lt0$ 이면 -1로 분류하겠습니다.
그럼 우리의 예측 $\hat{y} = \text{sign}(w^Tx)$ 가 되겠네요.

Training Data로

\{(x^{(i)}, y^{(i)}) : 1 \leq i \leq n\}

이 주어졌다고 합시다.

그리고, 손실함수를 다음과 같이 정의합니다.

E(\mathbf{w}) = \sum_{(x^{(i)}, y^{(i)}) \in \mathcal{D}} \max(-y^{(i)} \mathbf{w}^T \mathbf{x}^{(i)}, 0)

오분류한 샘플에 대해서는 손실이 일부 들어가고,
정분류한 샘플에 대해서는 손실이 0으로 들어갑니다.

모든 샘플에 대한 오류의 합이 E(w)네요.

아니면 이렇게 씁니다.
Perceptron Loss Function이에요.

E(\mathbf{w}) = -\sum_{(x^{(i)}, y^{(i)}) \in \mathcal{D}} y^{(i)} \mathbf{w}^\top \mathbf{x}^{(i)} \mathbb{I}[\text{mistake on } \mathbf{x}^{(i)}]

\mathbb{I}[\text{mistake on } \mathbf{x}^{(i)}] = \begin{cases} 1 & \text{if } y^{(i)} \neq \text{sign}(\mathbf{w}^\top \mathbf{x}^{(i)}) \\ 0 & \text{otherwise} \end{cases}

정답이 1이고, $w^Tx^{(i)}=0.5$ 인 경우에는 mistake가 없으니 error가 0으로 들어가고,
정답이 1이고 $w^Tx^{(i)}=-0.5$ 인 경우에는 오분류되었으니 error가 0.5로 들어가네요.
위의 식이랑 똑같아요.

정답이 1인데 -5로 예측하면 손실도 엄청 커질거구요.

좀 더 간결화해봅시다.
모델이 정답을 맞췄다면 Loss는 0으로 고려되니까, 덧셈에 들어갈 필요가 없습니다.

E(\mathbf{w}) = \sum_{(x^{(k)}, y^{(k)}) \in \mathcal{S}} -y^{(k)} (\mathbf{w}^T \mathbf{x}^{(k)})

로 간소화가 가능합니다.
이 때 $\mathcal{S}$ 는 오분류된 샘플의 Set입니다.
즉, 오분류된 경우에만 Error를 정의하겠다 라는 뜻이네요.

Property of Perceptron Loss Function

$\mathcal{S}$ 에 속하는 모든 sample $(x^{(k)}, y^{(k)})$ 에 대해 $-y^{(k)} (\mathbf{w}^T \mathbf{x}^{(k)}) > 0$ 이 성립합니다.
당연하죠. 오분류된 샘플이니까 y와 f를 곱하면 음수가 나올거고, 부호를 틀어주면 양수겠죠.

즉, $E(w) \geq 0$ 이 성립합니다.
만약 loss가 없는 optimal한 $w$ 를 찾았다면, $E(w) = 0$ 도 성립하겠죠.

그럼 이제 Loss function을 미분해봅시다.
그래야 그게 최소화되는 w를 구할테니까요.

E(\mathbf{w}) = \sum_{(x^{(k)}, y^{(k)}) \in \mathcal{S}} -y^{(k)} (\mathbf{w}^T \mathbf{x}^{(k)})

를 이용합시다.
$w^T$ 를 전개하면 다음과 같습니다.

\frac{\partial E(\mathbf{w})}{\partial w_j} = \sum_{(x^{(k)}, y^{(k)}) \in \mathcal{S}} \frac{\partial}{\partial w_j} \left(-y^{(k)} \left(w_0 x_0^{(k)} + \cdots + w_j x_j^{(k)} + \cdots + w_d x_d^{(k)}\right)\right)

w가 결국 d+1개의 원소를 가진 vector인데,
그 중 $w_j$ 만 가지고 편미분을 하면,
$w_jx_j^{(k)}$ 항 제외하면 전부 날아갑니다.

즉,

\frac{\partial E(\mathbf{w})}{\partial w_j} = \sum_{(x^{(k)}, y^{(k)}) \in \mathcal{S}} -y^{(k)} x_j^{(k)}, \quad \forall j = 0, 1, \dots, d

이 식이 성립합니다.

이제, Gradient를 구했으니 Perceptron을 학습할 수 있겠네요.

PLA (Perceptron Learning Algorithm)

우선 분류를 다 해보고, 틀린 샘플들을 $\mathcal{S}$ 에 넣어줍니다.
$\mathcal{S}$ 가 비어있다면 전부 정분류된거니까 넘어가고,
그렇지 않다면 아까 구한 gradient에 의해서,

$\Delta w = -\sum_{(x^{(k)}, y^{(k)}) \in \mathcal{S}} y^{(k)} x_j^{(k)}$
이 되고,
learning rate까지 적용하여
$w \larr w -\eta\Delta w$ 로 업데이트 해주면 됩니다.

Stochastic한 버전도 존재합니다.
$\hat{y}$ 를 구해서 $y^{(i)}$ 와 비교해보고, 틀렸다면,
그 즉시 $\Delta w = -y^{(i)}x^{(i)}$ 를 적용하여, 업데이트해주는 방식입니다.

암튼,

PLA는 맨 초기 $w$ 를 랜덤하게 잡고 시작하고,
positive sample을 오분류했다면 $w_{new} = w + \eta x^{(i)}$ 로 정의되고,
negative sample을 오분류했다면 $w_{new} = w - \eta x^{(i)}$ 로 정의됩니다.

이걸 오분류가 없을 때까지 반복하는거죠.

AND Operation

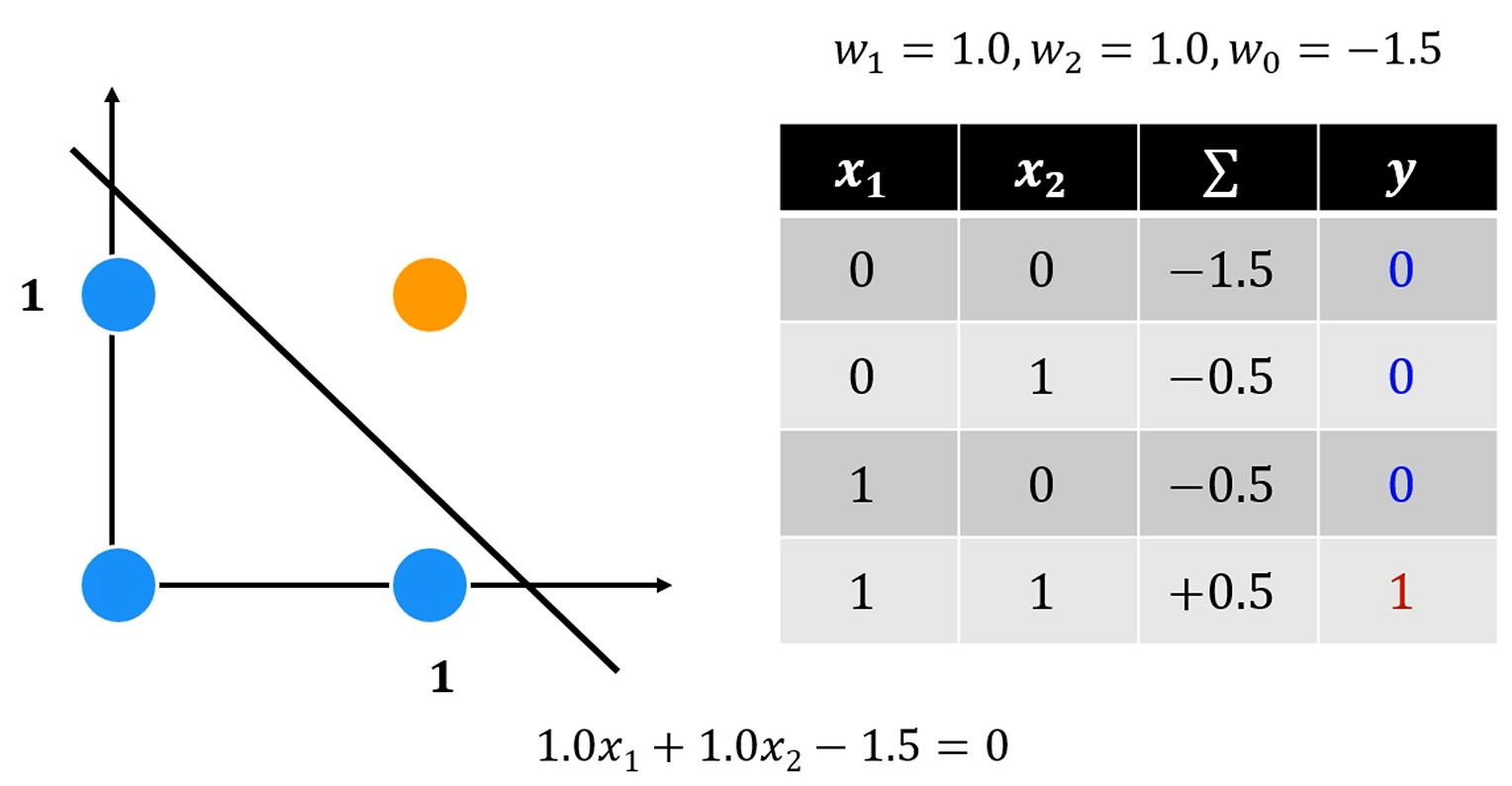
가장 기본적인 이진 논리게이트 중 하나입니다.
우리의 퍼셉트론인 $1.0x_1 + 1.0x_2 - 1.5 = 0$ 은 분류를 잘 했네요.

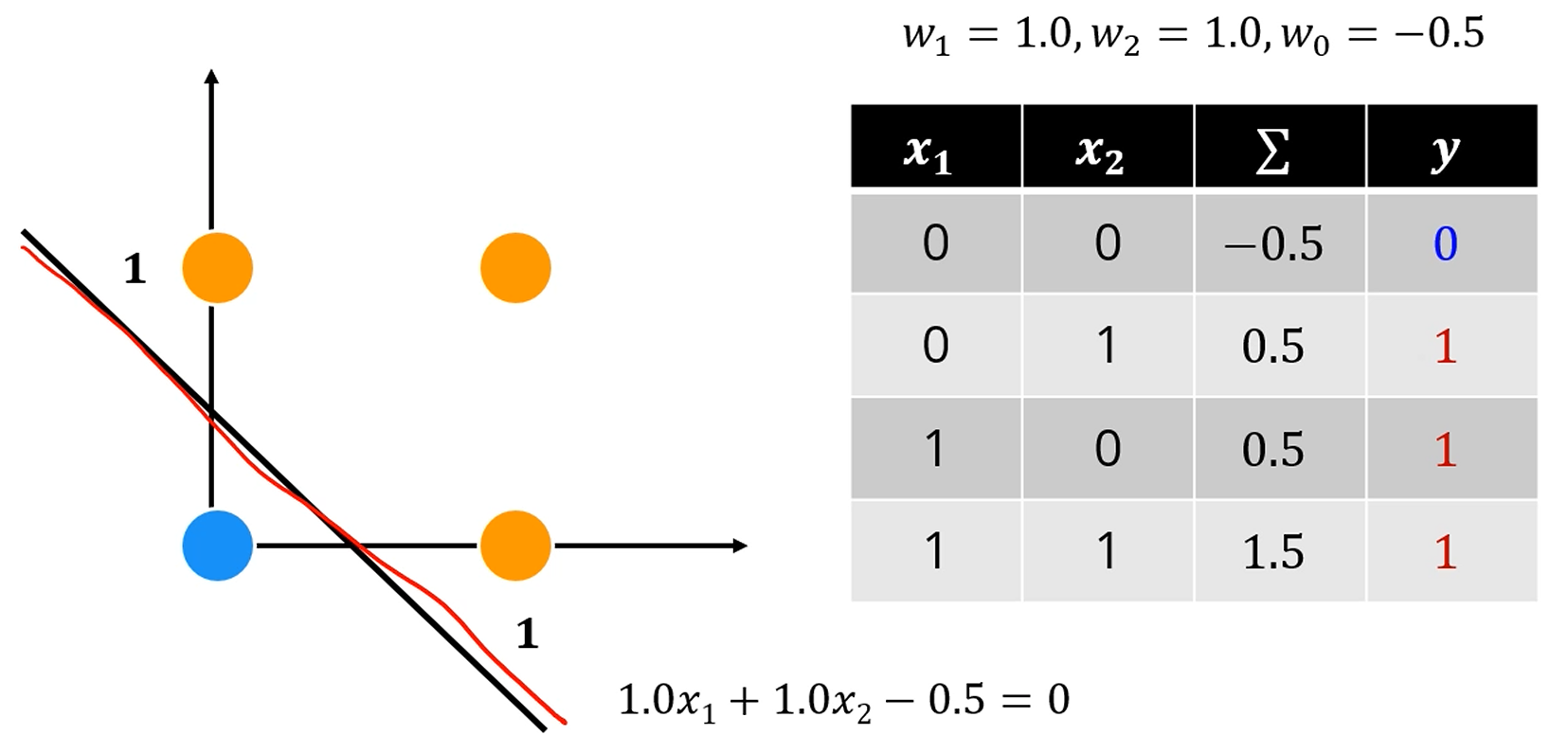
OR 게이트도 잘 표현이 되네요.

이런 식으로, PLA를 해서, PLA가 멈춘다면,
더이상 오분류가 없다는 뜻이고,
$\mathcal{D}$ 가 Linearly Separable하다는 뜻과도 같습니다.

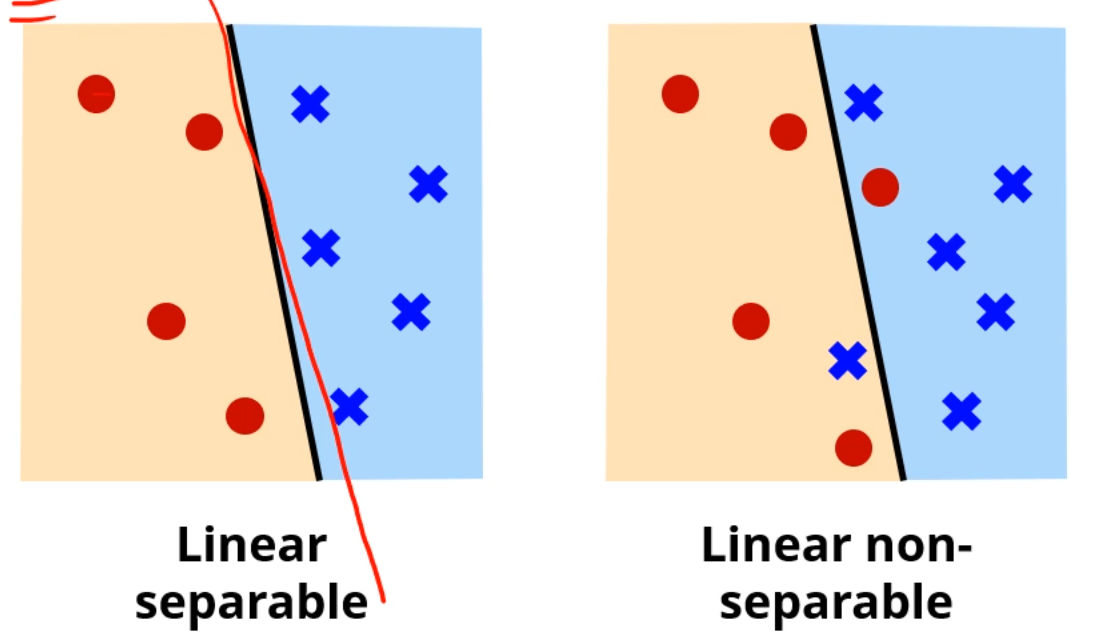
전자는 PLA를 계속 조지다보면 언젠가 PLA가 멈출텐데,
후자는.. 아마 멈추지 않을겁니다.

XOR Operation

되게 간단한 논리 Gate인데, 퍼셉트론으로는 절대 분류가 불가능한 문제입니다.

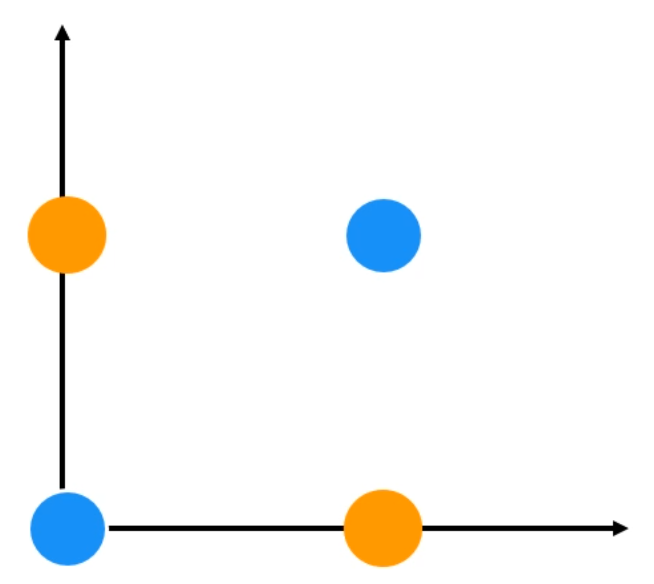
이걸 해결하기 위해 MLP가 등장합니다.

MLP (Multi-Layer Perceptron)

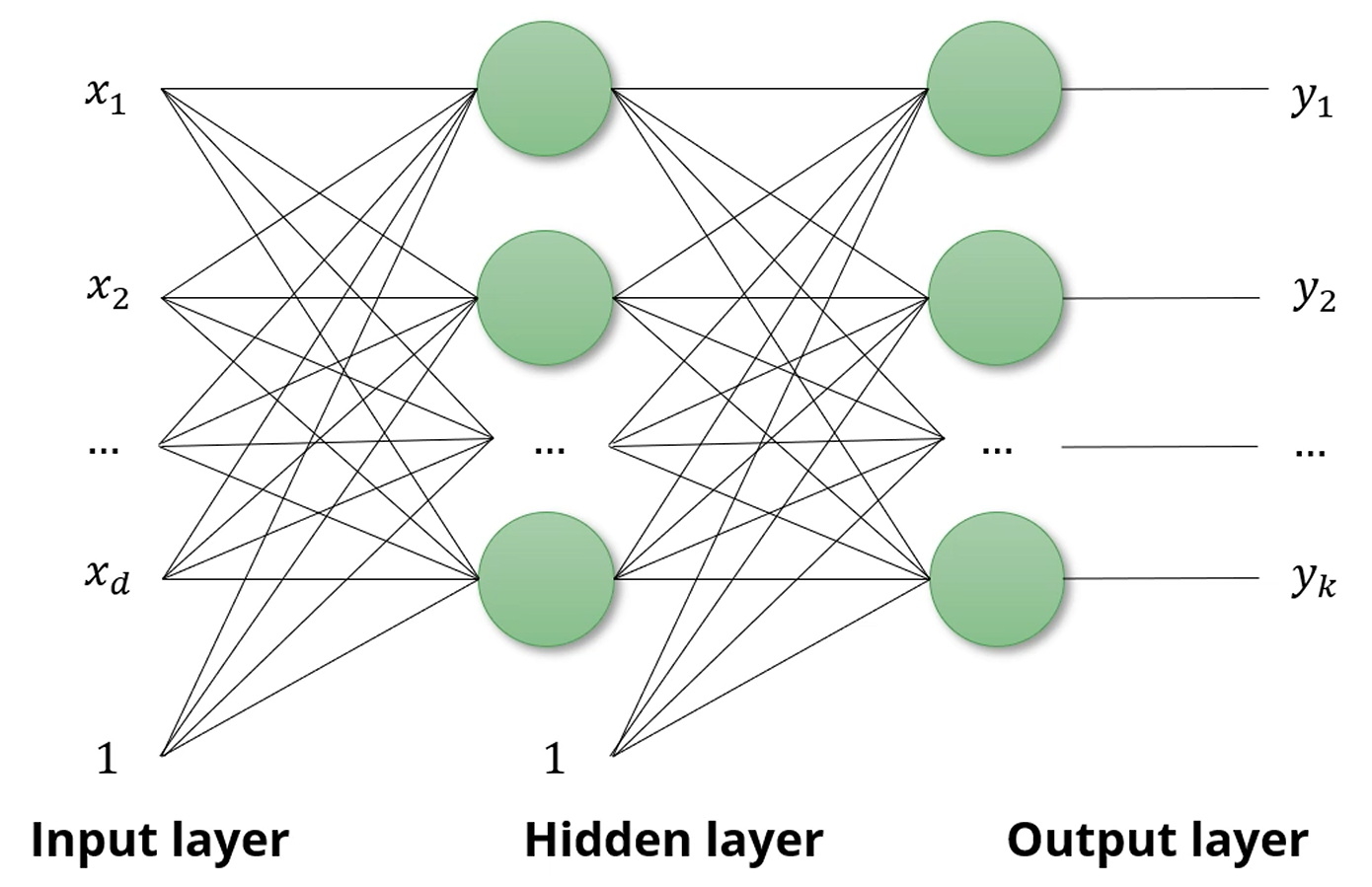
퍼셉트론을 여러 층으로 쌓아서 더 복잡한 문제를 푸는 방식입니다.
MLP를 Feed-Forward Neural Network라고도 불러요.

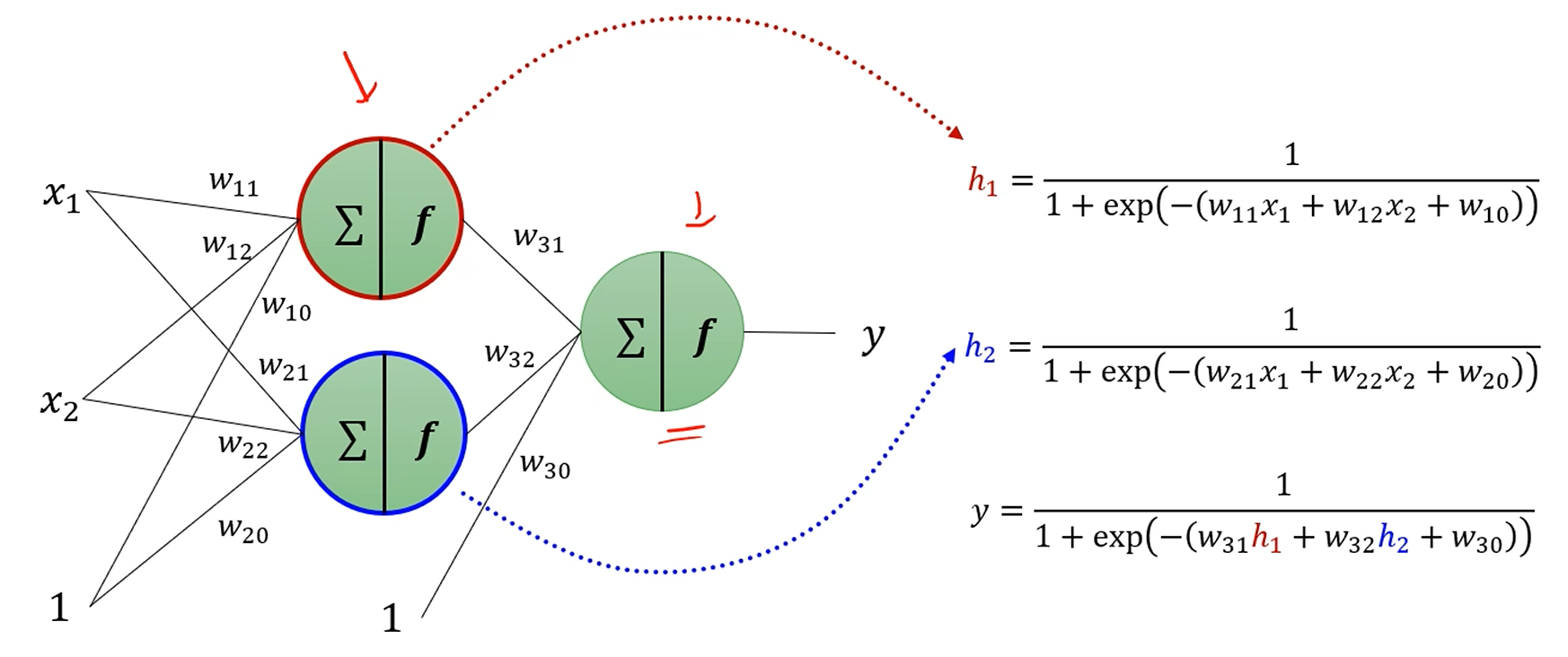
MLP를 자세히 봅시다.
은닉층이 1개에 뉴런 2개, 출력층도 뉴런 1개짜리 간단한 놈인데,
이걸로 xor가 구현이 가능합니다.

MLP에선 Single Perceptron과는 다른 Sigmoid Activation fuction을 씁시다.
$\sigma(x) = \frac{1}{1+e^{-x}}$ 임을 참고하면,

위쪽 뉴런이 뱉는 값은 $\frac{1}{1+e^{-(w_{11}x_1+w_{12}x_2+w_{10})}}$ 이고,
밑에 뉴런이 뱉는 값은 $\frac{1}{1+e^{-(w_{21}x_1+w_{22}x_2+w_{20})}}$ 이고,
둘이 합쳐진 출력층 뉴런이 뱉는 값은 $\frac{1}{1+e^{-(w_{31}h_1+w_{32}h_2+w_{30})}}$ 입니다.

$h_1, h_2$ 에 각각 값을 대입하면

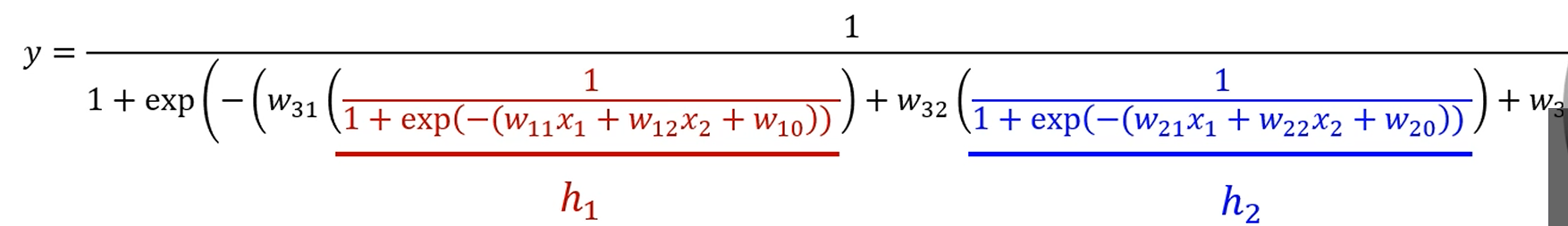
이런 괴상망측한 식이 나오는데, 사실 별건 아니에요.
그냥 선형결합 + sigmoid를 쭉 전개했을 뿐입니다.

XOR using MLP

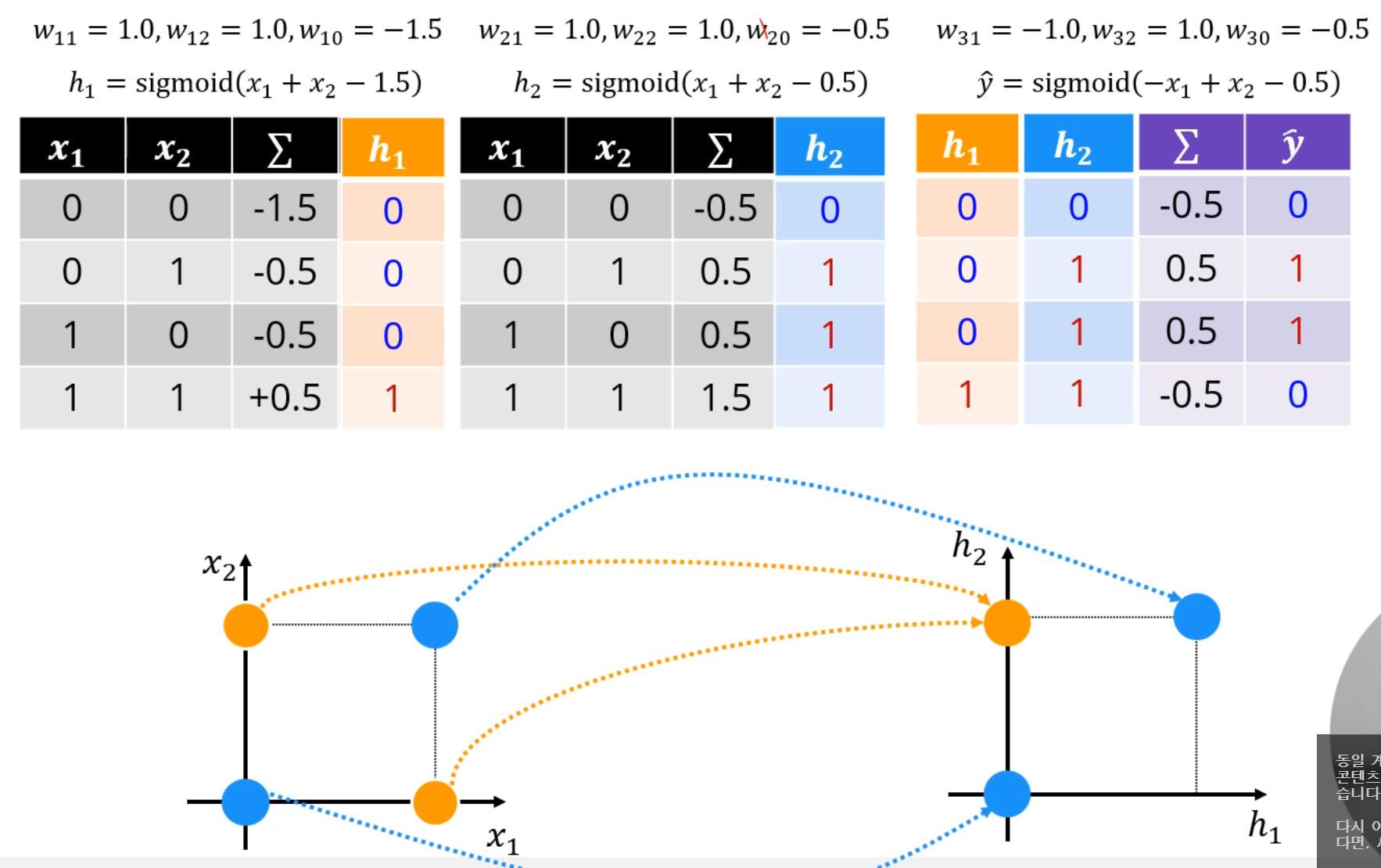
세 개의 퍼셉트론을 만들었습니다.
$x_1+x_2-1.5$ , $x_1+x_2-0.5$ , $-x_1+x_2-0.5$
그리고 앞의 2개 퍼셉트론에 sigmoid까지 적용한 값을 각 $h_1, h_2$ 로 삼은 후,
그 값들을 input으로 삼아 마지막 퍼셉트론이 값을 출력하게 했습니다.

그러면 결국 ((0,0), (0,1), (1,0), (1,1))을 넣어 (0, 1, 1, 0)의 출력이 만들어졌네요.

오, 그러면 이런것도 MLP로 쪼갤 수 있나요?

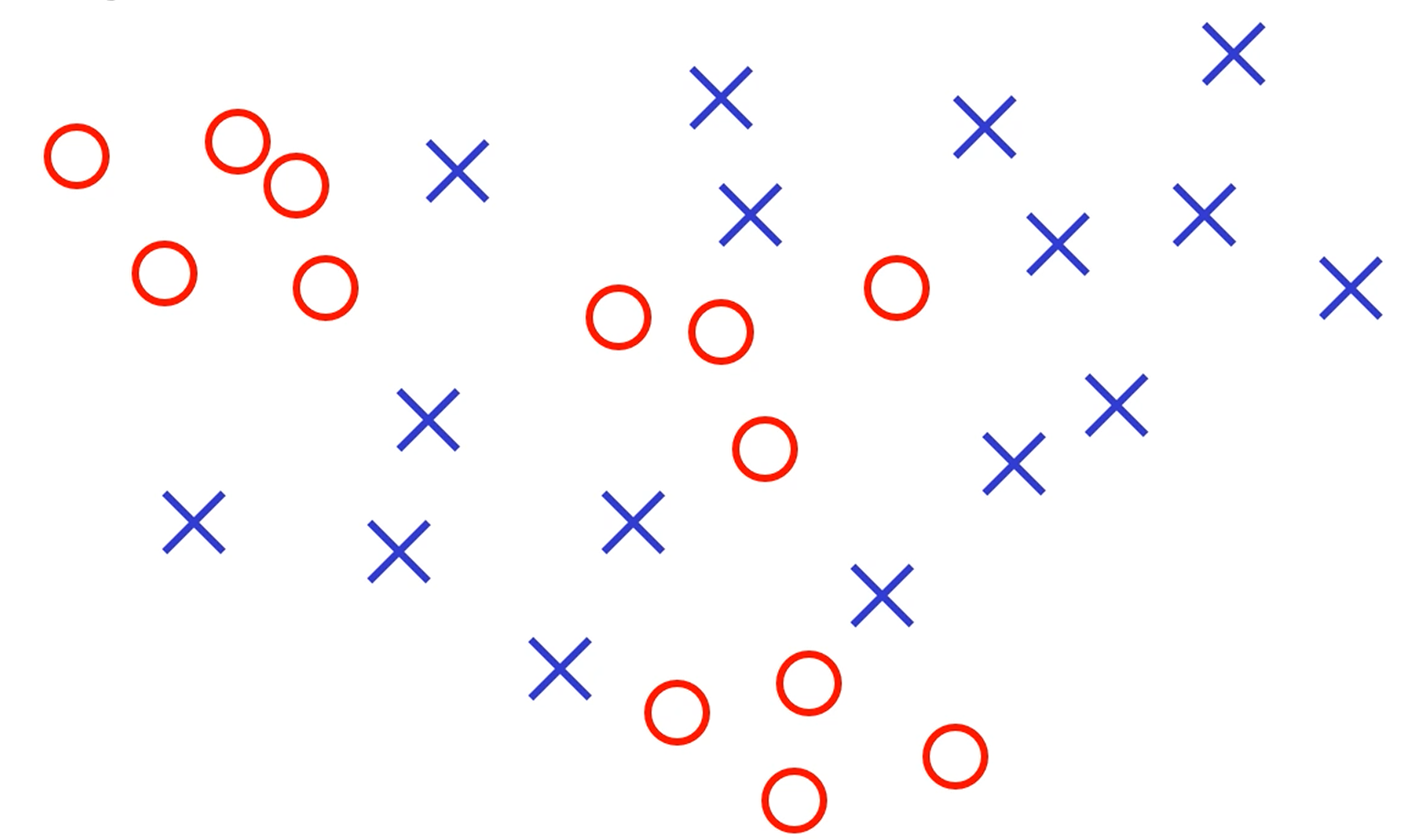
이건 좀 경계가 괴랄맞죠?

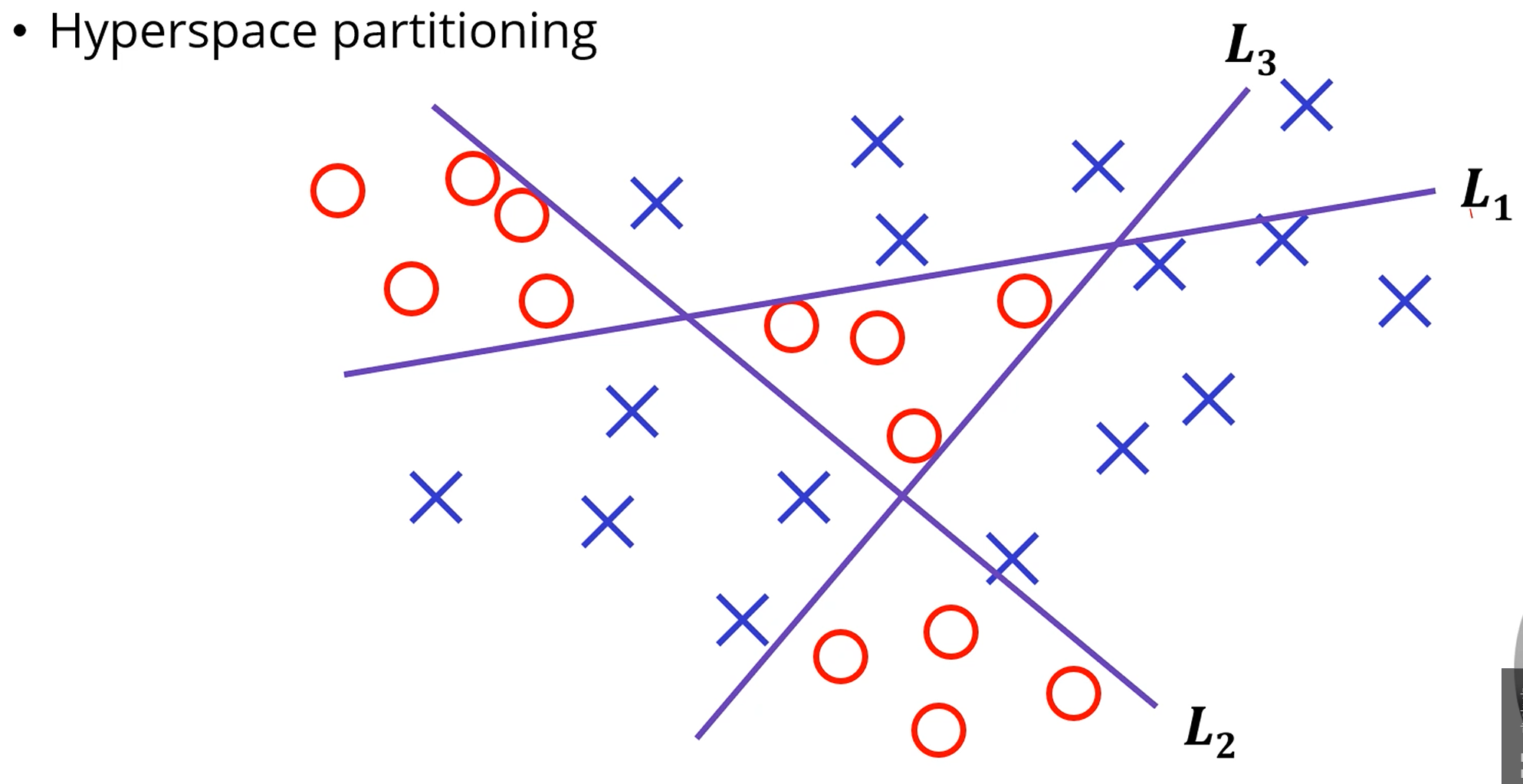
다음과 같이 3개의 퍼셉트론으로 나눌 수 있게 학습을 시켜서,

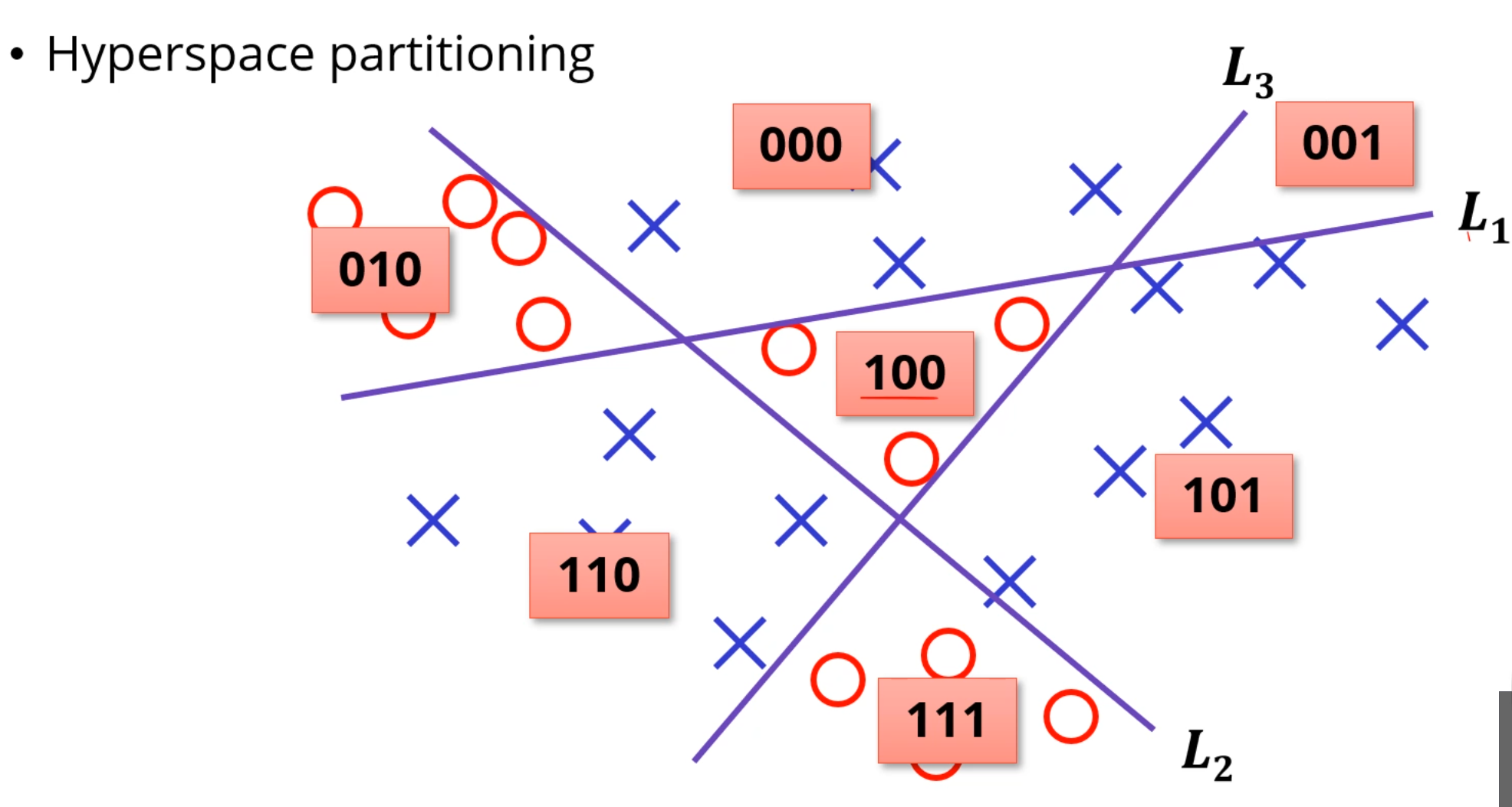
각 공간의 위치에 맞게 Indexing을 시킵니다.
그러면 이제 [010], [100], [111] 벡터만 찾아내는 문제로 바뀌었습니다.

Recap- ML 1-2-3

데이터를 수집하고 feature 추출하여 데이터를 벡터로 바꿉니다.
모델 $\mathcal {H}$ 와 loss function $\mathcal {L}$ 을 세웁니다.
Loss를 최소화하는 optimal parameter를 구합니다.

...
[1]번부터 따져봅시다. 데이터에서 feature를 어떻게 찾고 벡터화 할까요?

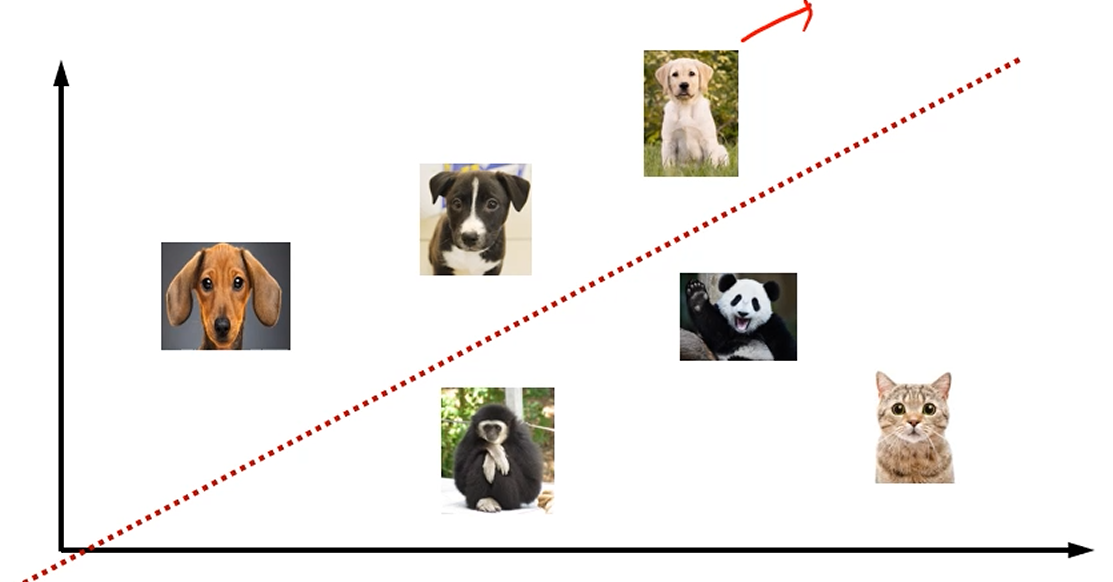
정말 무식하게, 강아지 분류기를 만들고 싶을 때, Dog와 Not Dog로 나눌 수 있지요.

문제는, 원래 데이터가 Linearly Separable하지 않다면,
Perceptron을 써도 정확한 분류가 되지 않는 경우가 많습니다.

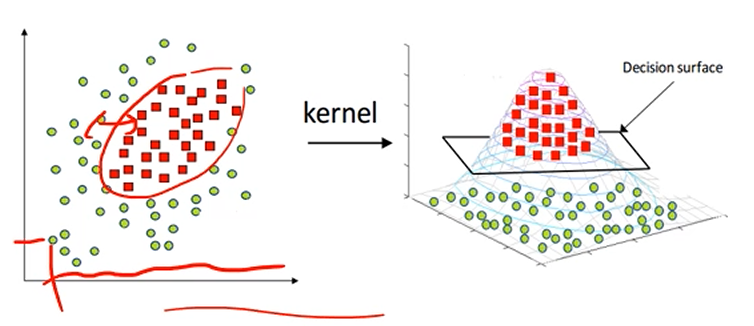
이렇게, 커널함수를 이용해 데이터를 새로운 공간에 매핑할 수 있습니다.
이러면 이제 Decision 'Surface'를 구하는 문제로 바꿀 수가 있죠.
이렇게 변환을 해주면 선형 machine으로도 충분히 분류가 가능해지게 됩니다.

어떤 입력에서 어떤 feature가 중요한지를 찾아내는것까지도
ML 모델이 학습해서 분류할 수 있습니다.

수동으로 만든 feature는 만들기도 오래 걸리고, 검증도 오래 걸리고,
그리고 인간이 만든거라 온전하지 않을 수도 있습니다.

근데 데이터에서 학습된 feature는 학습하기도 쉽고, task에 적합한 feature가 학습되게 됩니다.

그래서, task에 적합한 feature를 만드는데 드는 시간을 ML 모델의 구조를 결정하는데 드는 시간으로 사용 할 수 있게 됩니다.
그러면 그 이쁜 구조로 구성된 ML 모델이 이쁜 feature를 잘 골라주는거에요.

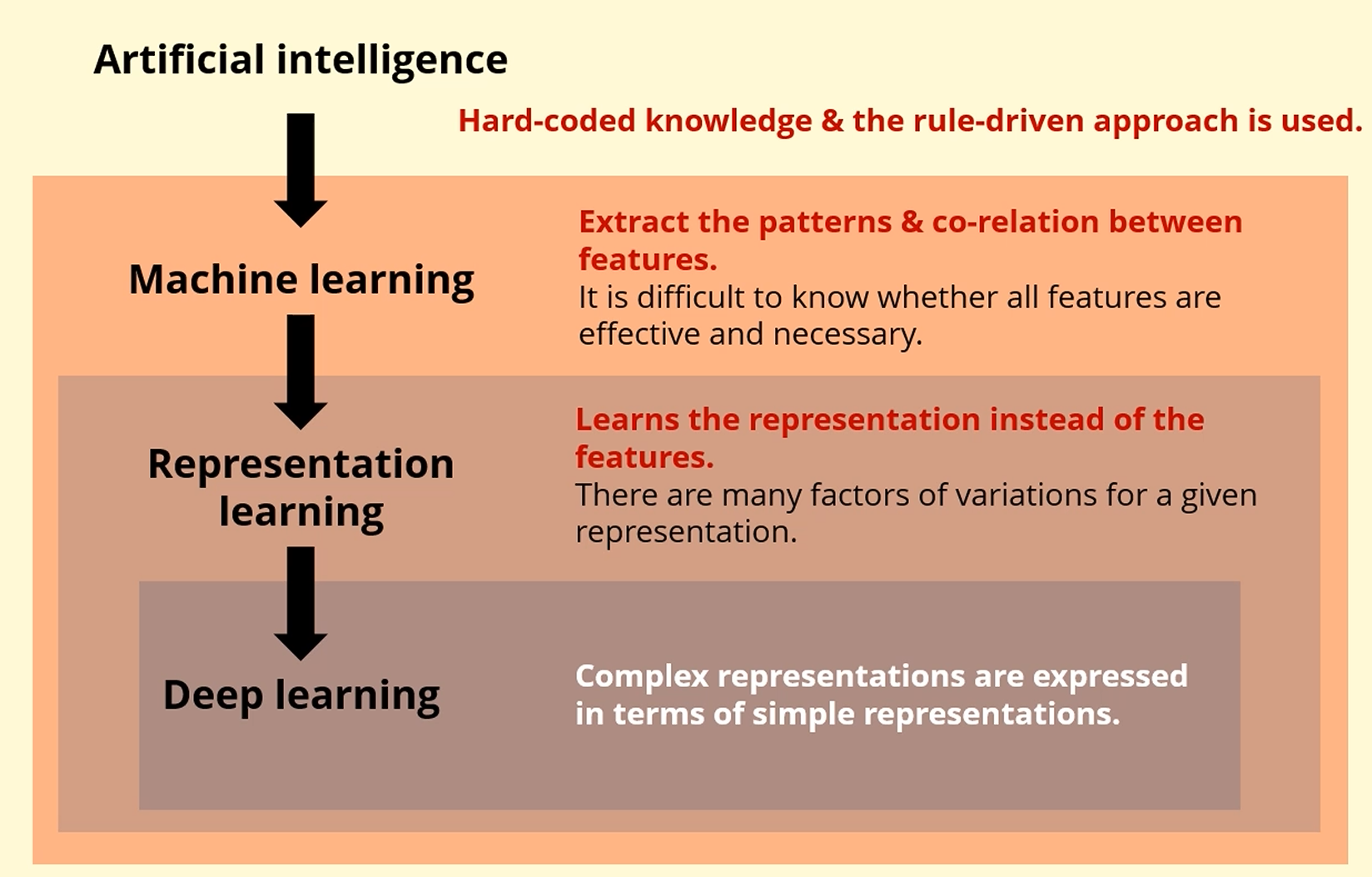
전체 AI가 있고,
통계적 기법을 적용하여 데이터로부터 패턴을 뽑아내고, 학습하는게 ML이며,

feature를 그대로 쓰지 않고, feature의 비선형적 변환을 통해
더 task를 수행하기 쉬운 공간으로 표현하는 것이 RL (Representation Learning)이고,
(t-SNE, Dimensional Reduction)
그 안에 존재하는게 딥러닝입니다.

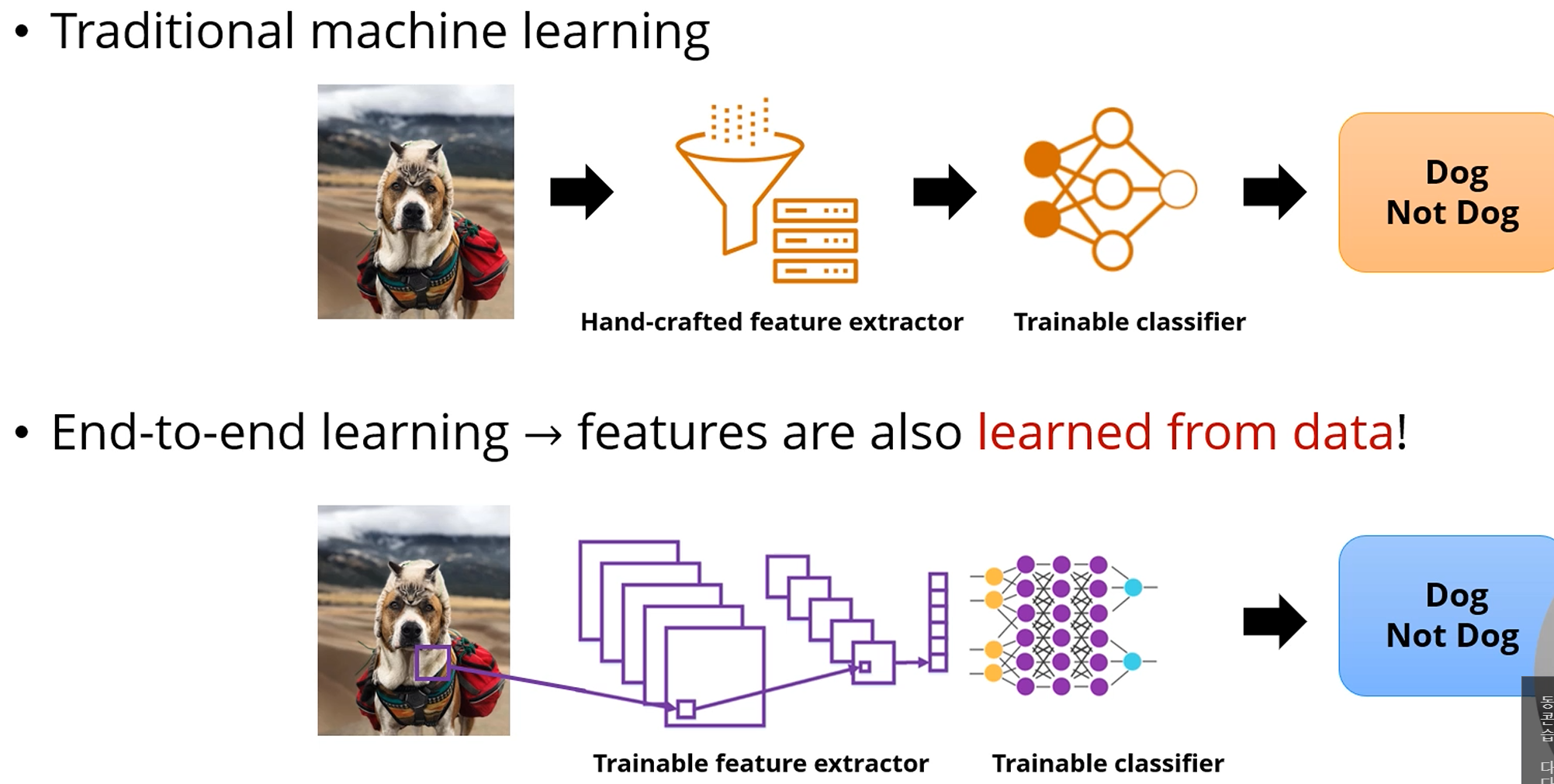
위쪽이 우리가 배운 ML (Shallow Learning)입니다.
입력을 그대로 쓰던가, feature를 좀 뽑아내서,
hypothesis function에 따라서 classifier를 세워서 학습시킵니다.

Deep Learning에서는,
입력에서부터 유용한 feature를 뽑아내는 것이, 자동적으로 이뤄지며
classifier를 통해 학습됩니다.

차이점은 '입력'을 넣기만 하면 자동으로 '출력'이 나오는 정도가 되겠습니다.
인간이 굳이 입력 feature에 대한 조정을 해 줄 필요가 없죠.

DNN(Deep Neural Networks)

DNN의 함수들은 '표현'을 학습합니다.

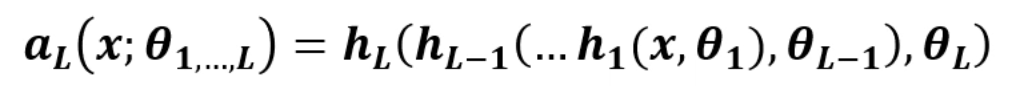
입력 x에 대해, $h_1$ 이라는 첫번째 계층을 통과시킵니다. ( $h_1(x, \theta_1))$
두번째 계층 $h_2$ 은 $h_1$ 의 output을 입력으로 받습니다.
자기 자신의 변환을 적용해서요. ( $\theta_2$ )
이렇게 쭉~~ 진행이 되는겁니다.
마지막에는 $h_{L-1}$ 에 대해 $\theta_L$ 이라는 변환을 적용시켜서
최종 결과물인 $h_L$ 을 얻어냅니다.

이렇게 생긴 함수를 심층신경망이라고 부릅니다.

각각의 모듈이 순서대로 진행되기에, hierarchical하며,
각각의 모듈에서 진행되는 일은 비선형적입니다.

단순 선형결합만 하는 건 DNN이라고 할 수 없죠.
모듈 1이 $x$ 에 $A$ 를 선형결합해 $Ax$ 를 만들고,
모듈 2가 거기에 $B$ 를 선형결합해 $BAx$ 를 만든다면,
그건 모듈 2개를 쓸 이유가 없죠. 그냥 $BA$ 를 선형결합시키는 단층 모듈로 표현이 되죠.

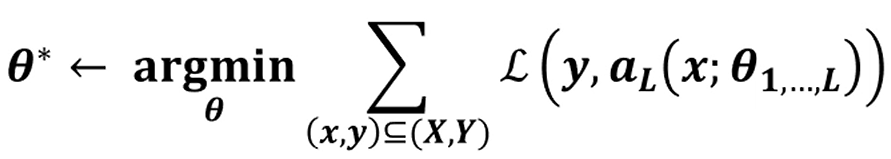
그 후로는 똑같습니다.
Loss Function을 정의하여, 정답과의 차이를 최소화하는
$\theta$ 를 찾는 것이 학습의 목표가 됩니다.

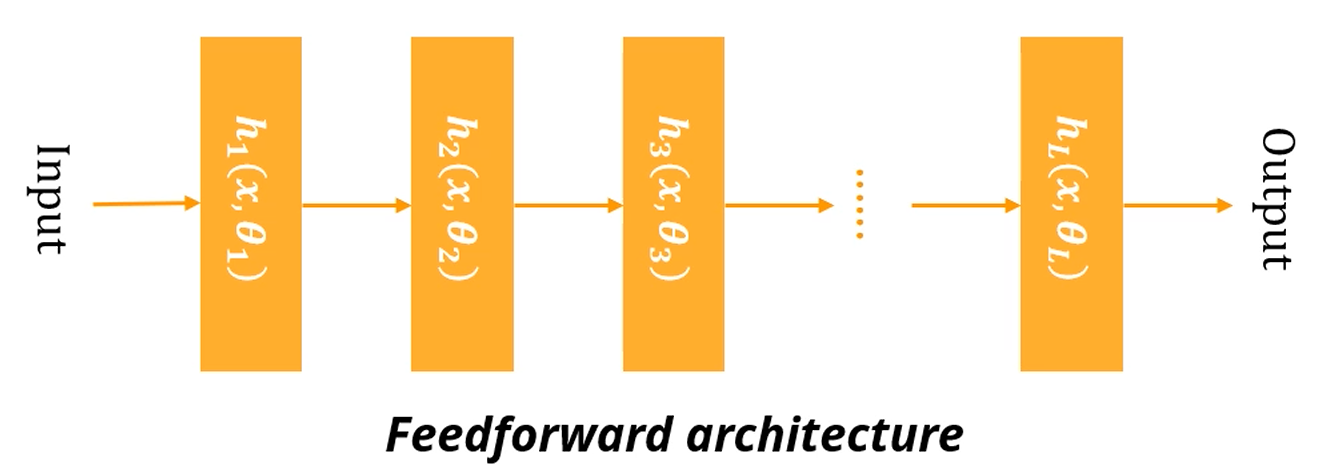
이런 단순한 FeedForward architecture만 고려를 하기로 합시다.

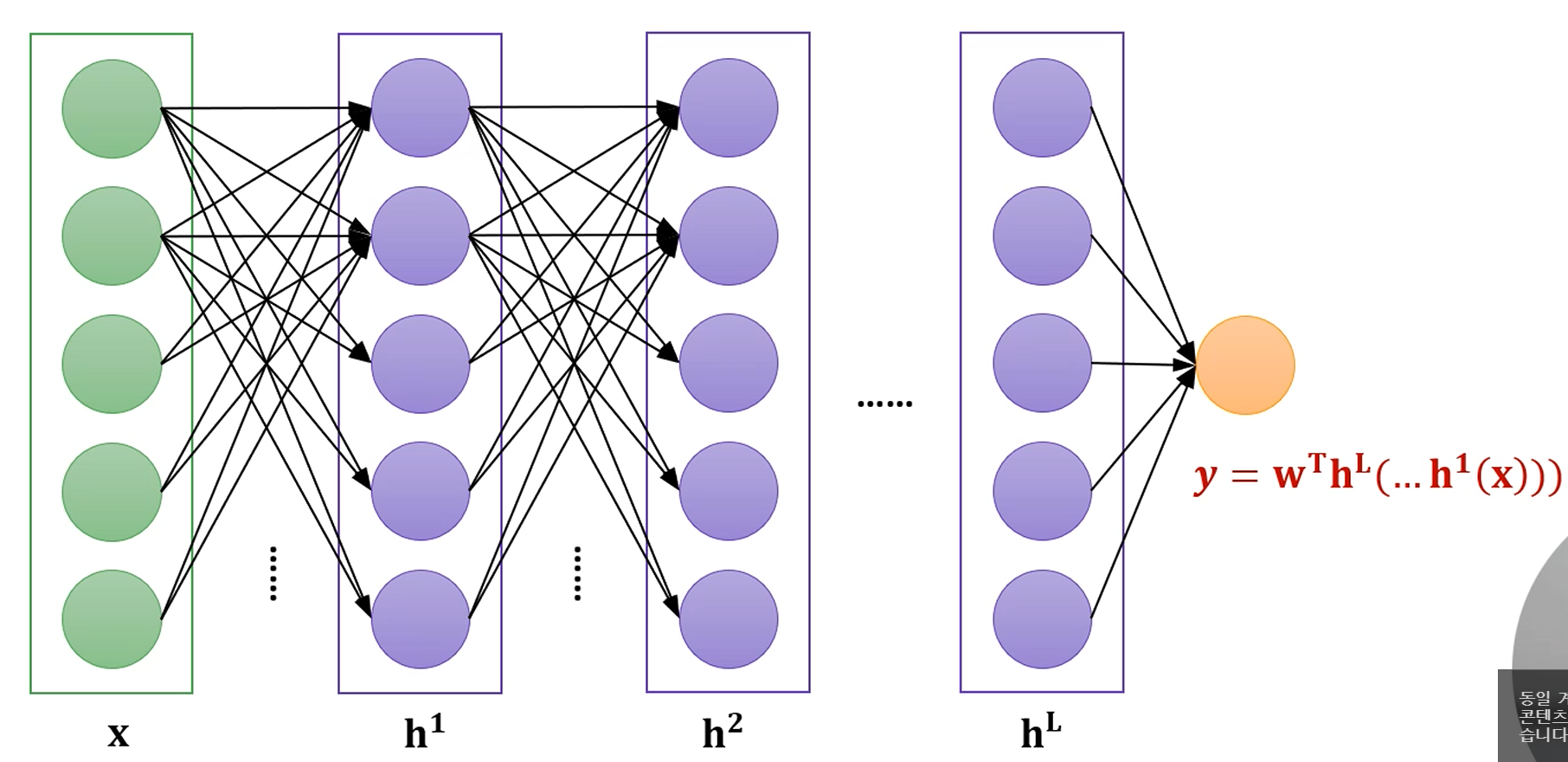
조금 더 확대를 하면, 입력 $x$ 가 여러 모듈을 거쳐서,
Hidden Layer를 거쳐 수많은 결합들이 일어나고, 마지막으로 하나의 출력층을 거쳐 출력으로 변환되는 그런 모듈 구조라고 생각하면 될 것 같습니다.
이 경우는 [5차원]이 [1차원]으로 변환이 되네요.
Regression이 될 수도 있고, Classification 문제일 수도 있겠네요.

은닉층은 임의로 5차원으로 가정했습니다.
하지만 은닉층의 차원이나 개수는 알아서 조정하기 나름입니다.

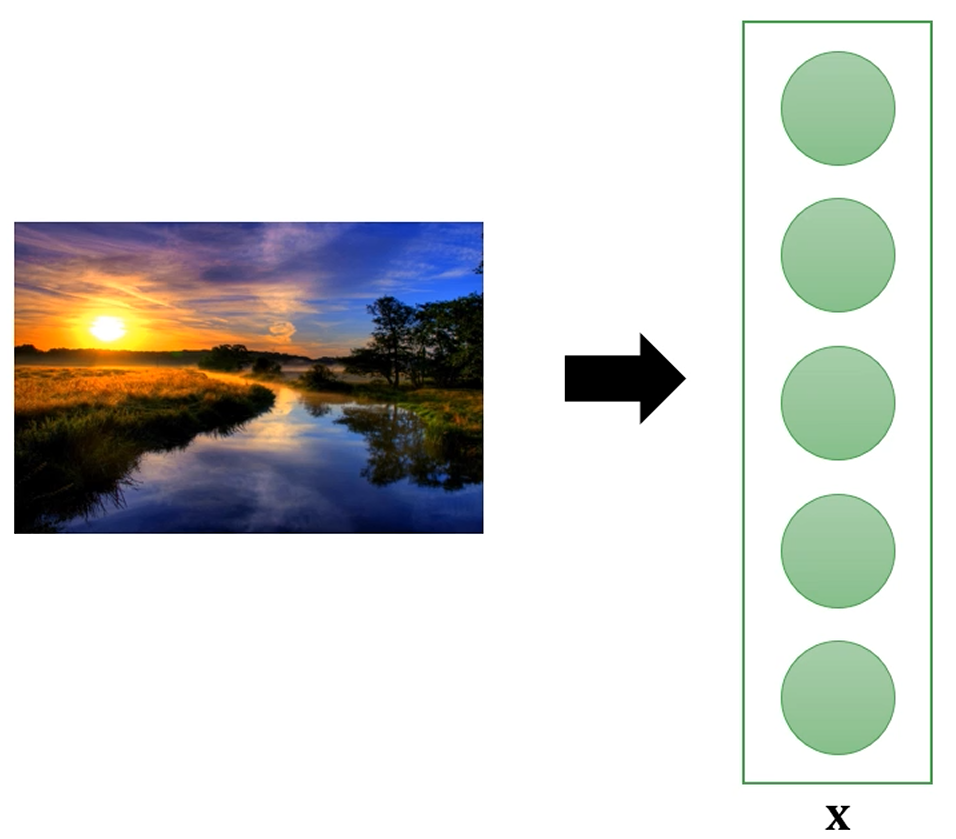
입력 데이터를 vector로 표현할 수 있습니다.
입력 데이터를 입력층에 약간의 정규화만 거친 후에 넣어주면,
feature extraction같은 건 hidden layer에서 알아서 진행하게끔 구성이 된겁니다.

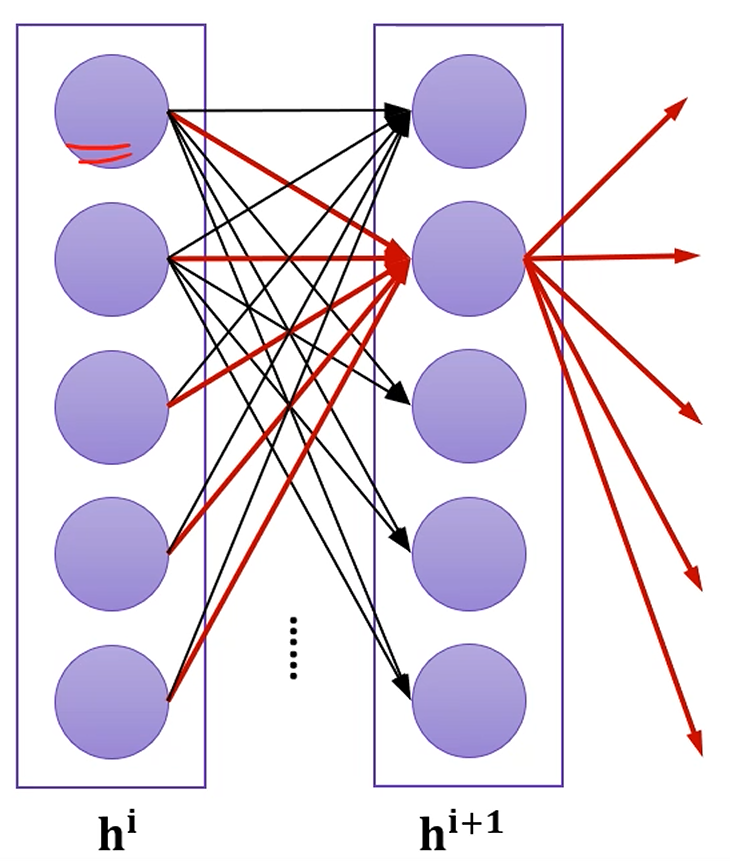
각각의 hidden layer는 이전 층의 출력을 입력으로 받아서, 선형결합을 알아서 해서, activation function을 적용하여 이후 layer로 출력해주는 형태를 가집니다.

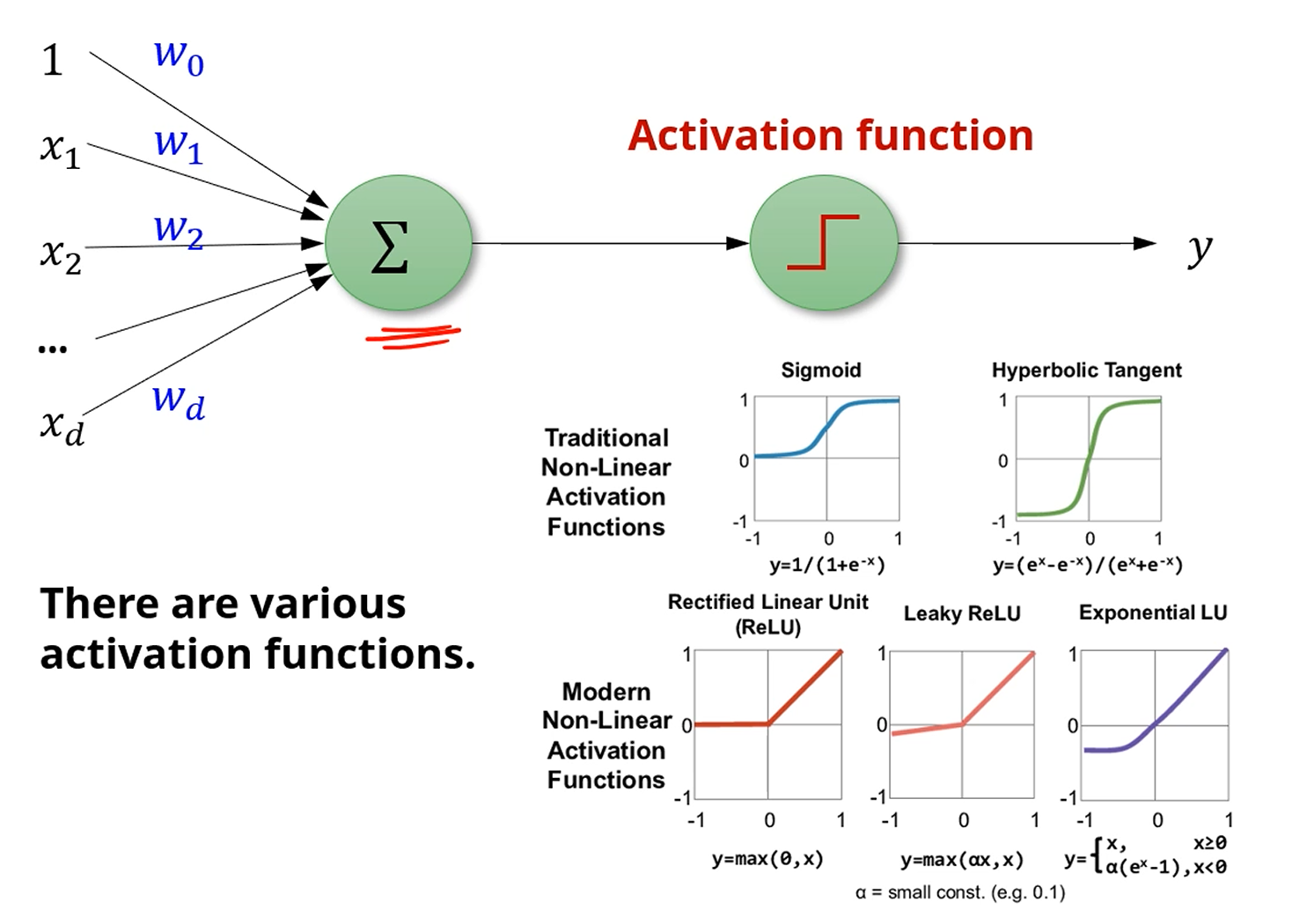
하나의 node에서 발생하는 일은 perceptron과 지극히 동일합니다.
이전 layer로부터 받은 데이터를 선형결합 하여, Activation Function을 적용하여 비선형성을 추가하고,
activate시킵니다.

이 때 activation function은 step function을 쓰지 않고, 연속적으로 기울기가 0이 되지 않는
sigmoid나 Hyperbolic Tangent 정도를 사용합니다.

최근에는 좀 더 구현이 쉬운 ReLU,
그리고 $x<0$ 에서 학습이 일어나지 않는 문제점을 개선한 Leaky ReLU, Expeonential LU 등을 사용하는 추세입니다.

뭐가 됐든, 비선형성을 추가한다는 점이 핵심입니다.

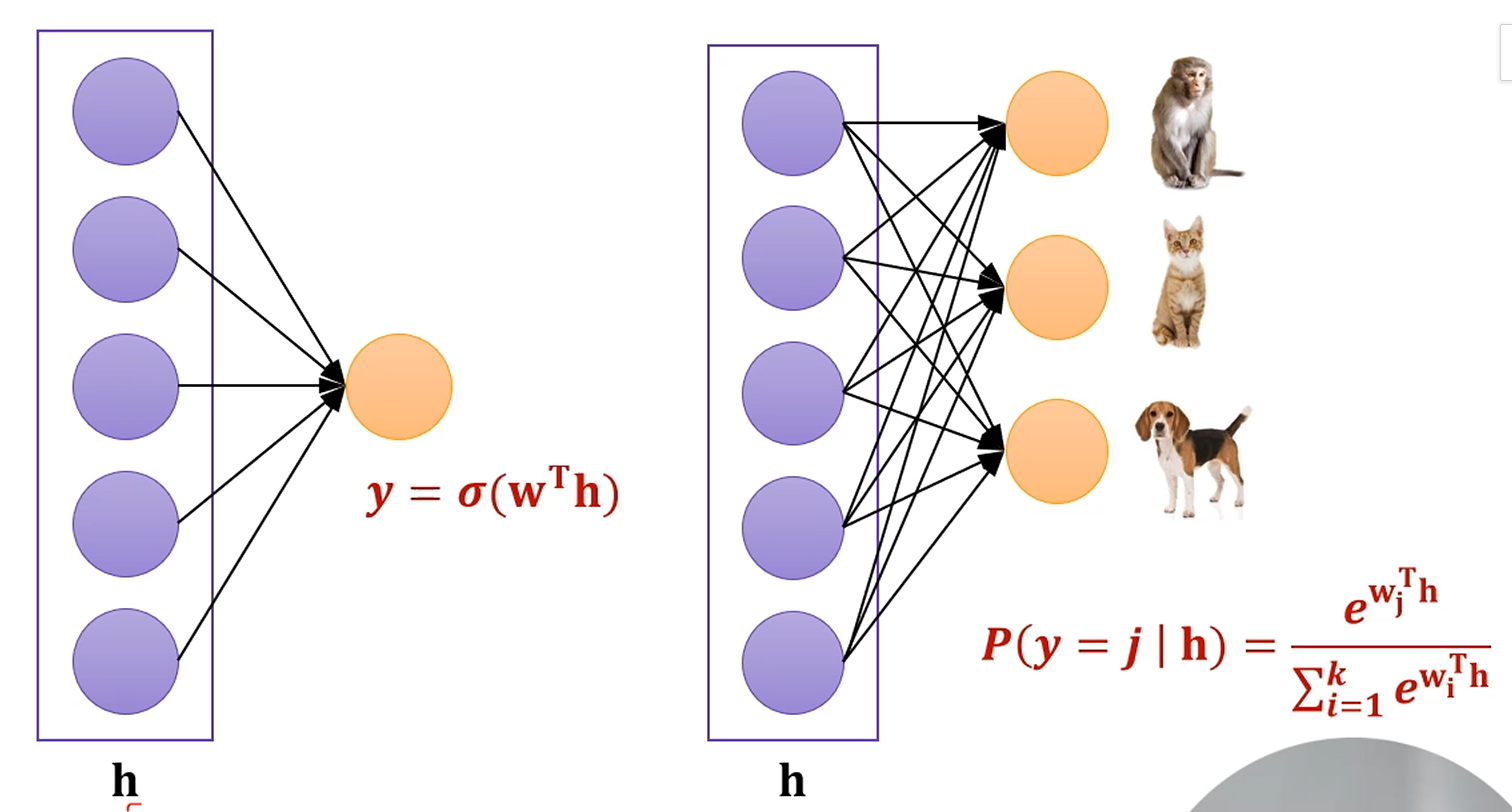
Output layer에서는 layer의 값을 적당히 잘 조절하여 출력을 만들면 됩니다.
Regression 문제라면 그냥 선형결합을 시켜주면 되고,
Binary Classification 문제라면 Sigmoid를 적용시켜주면 됩니다.
거기서 나온 값이 Positive Class로 분류될 확률로 해석됩니다.

다분류 문제라면 마지막에 선형결합된 결과가
각 Class로 분류될 확률로 해석됩니다.

이렇게 각각의 Layer를 만드는거고요.

데이터를 얻고,
모델을 정의하고 weight를 initialize하며,
현재 model을 이용해 값을 출력하고,
그 출력 값을 이용하는걸 Forward Computation 또는 Forward Propagation이라 합니다.

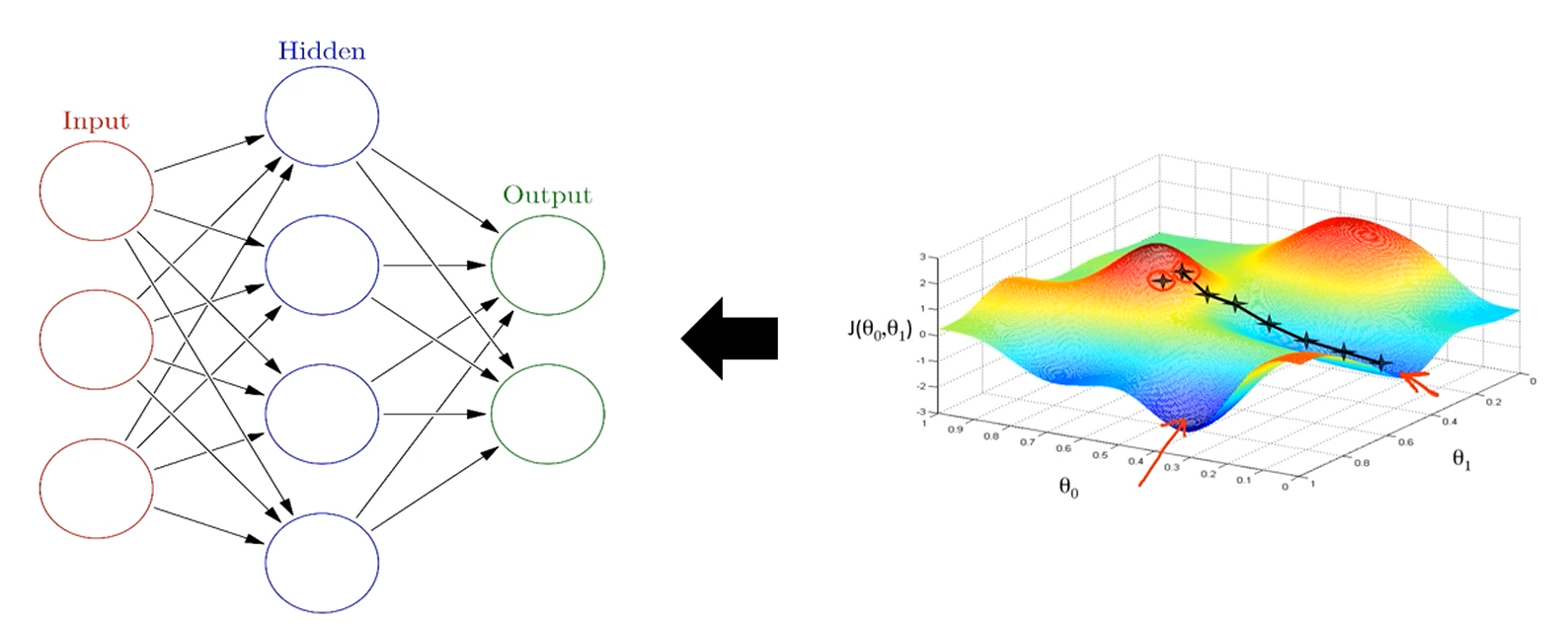
반대 방향으로,
$\hat{y}$ 와 $y$ 를 비교하여 무언가 loss를 적용하고,
Error를 수치화 한 후 그 오차만큼 weight를 수정해주는 방식.

이것을 Backward Computation이라고 합니다.

가령, Error를 $L$ 이라고 하면,
$i$ 번째 layer의 $j$ 번째 node의 $k$ 번째 weight인 $w_{ijk}$ 가 $L$ 에 기여하는 정도를 찾아서,
- $\frac{\partial L}{\partial w_{ijk}}$ 를 weight에 추가해주면 weight가 작아지는 방향으로 이동할 것입니다.