SVM을 배우려면, 많은 선행지식이 필요합니다.
Hard-Margin, Soft-Margin,
Vector Derivative,
Lagrangian,
KKT,
Duality,
Optimization . . .
거기 몰두되지 않는게 중요합니다.
Goal
어쨌든, SVM의 목표는
이진분류를 수행하는 초평면을 찾는게 목표입니다.
근데, 그 수많은 선들 중 'margin'이 큰 선이 더 좋습니다.
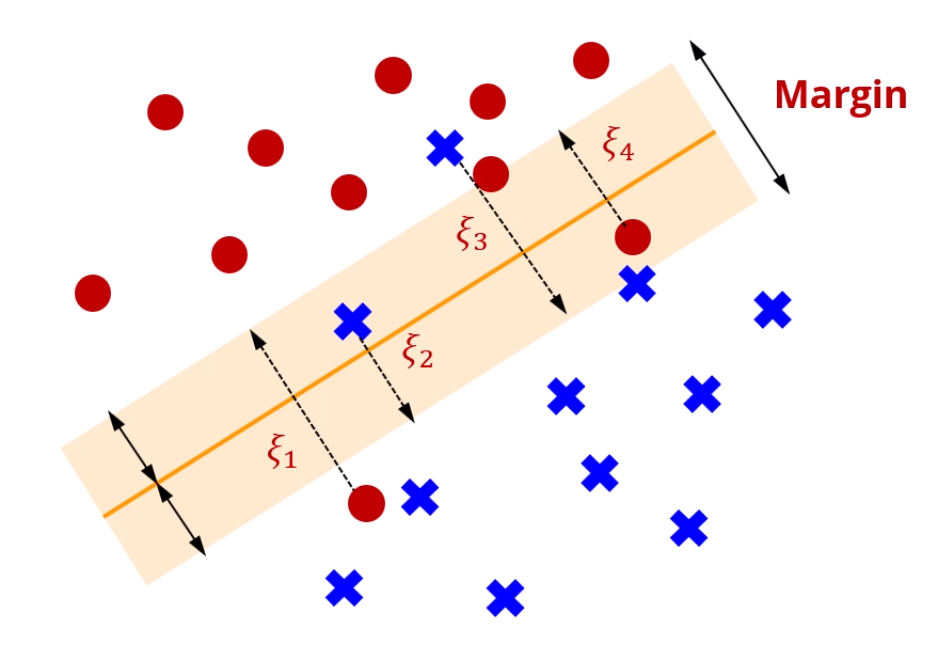
제대로 분류되지 않은 점은요?
자기가 원래 있어야 하는 영역과의 거리가 가까울수록 좋습니다.
그 오차치를 로 정의했구요.
그래서, 목표가 2개가 생깁니다.
- 정분류된 점들과의 거리는 멀 수록 좋은 선입니다.
- 오분류된 점들은 본인이 있어야 할 영역과 가까울 수록 좋은 선입니다.
이 두 목표를 정량화하고, 가중합을 치면 전체 손실이 계산됩니다.
그래서,
-
목표1, 목표2를 정량화하고, 부등식 조건이 있는 최적화 문제로 표현
-
그 표현을 위한 라그랑지안 도출
이 때, 목적함수는 "L의 최댓값을 최소화한다", 즉
가 됨 -
Duality를 활용하여 max와 min의 위치를 변환
가 됨 -
KTT 조건을 활용하여 안쪽 min 문제를 해결
-
남은 max 문제는 컴퓨터로 해결하여 를 구함
-
그 로 를 구함
이게 끝입니다.
이거 6단계만 다 할줄 알면 SVM을 알게 됩니다.
추가로 꼭 알아야 하지만, 처음 배울 때에는 알면 방해가 될 수 있는 부분들은
다음과 같습니다.
- Min-max inequality 예시
- KKT조건 예시 문제
- SVM이 Hinge loss와 L2 Regularization을 적용한 문제와 동일함을 보이기
- SVM여부를 로 판단하기
- Hard-margin과 Soft-margin의 차이, 그리고 이 차이로 인해 라는 조건이 추가되는 것
- Kernel trick과 Kernel trick을 이용하면 w를 계산은 못해도 분류는 할 수 있다는 것
목표1, 목표2 정량화 후 수식 표현
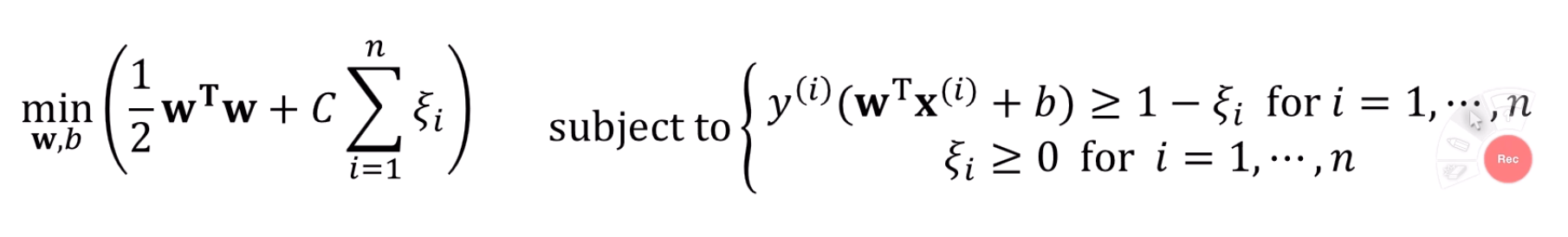
least margin은 최대화 하고, 합을 최소화 하는 것은 다음과 같이 표현됩니다.
물론, 이 때 두가지 조건이 붙습니다.
라그랑지안 도출

이 내용을, 라그랑지안을 도출하여 적습니다.
목적함수를 그대로 적으면 됩니다.
Duality 이용
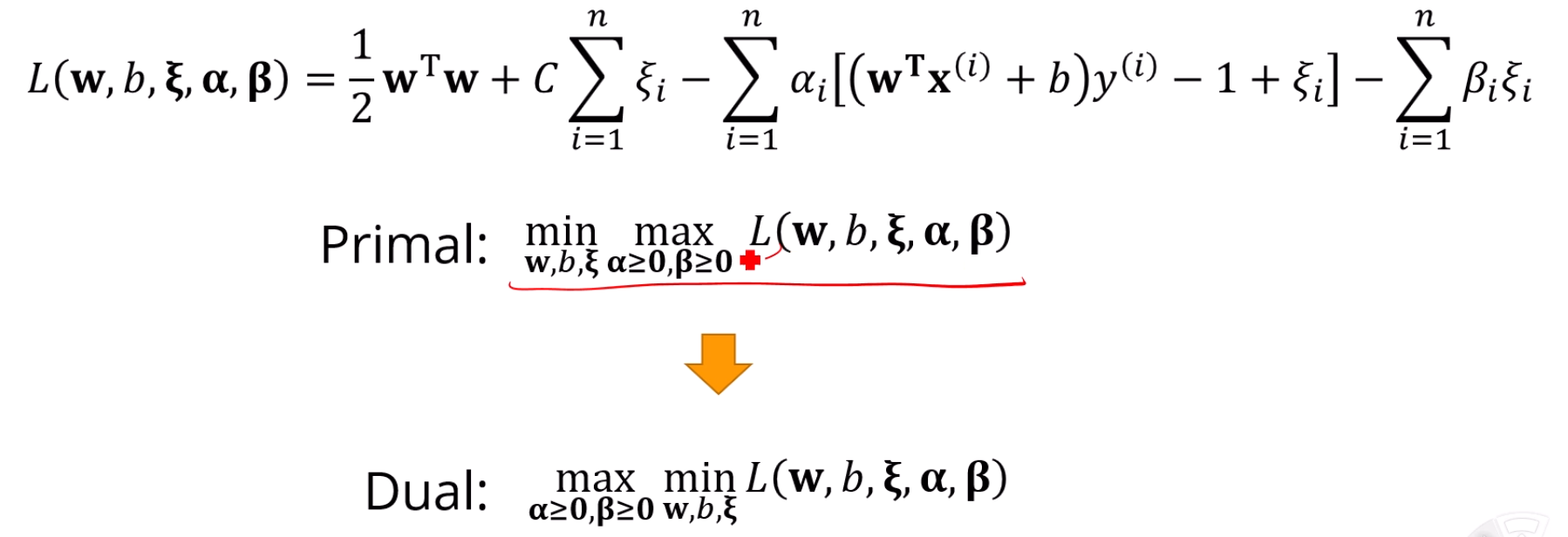
에 대해 Duality를 적용하여 min-max를 max-min으로 바꿔줍니다.
이 convex하기 때문에 가능하다는 조건이 숨어있는데, 그건 일단 가정만 하고 갑시다.
안쪽 min 문제 해결
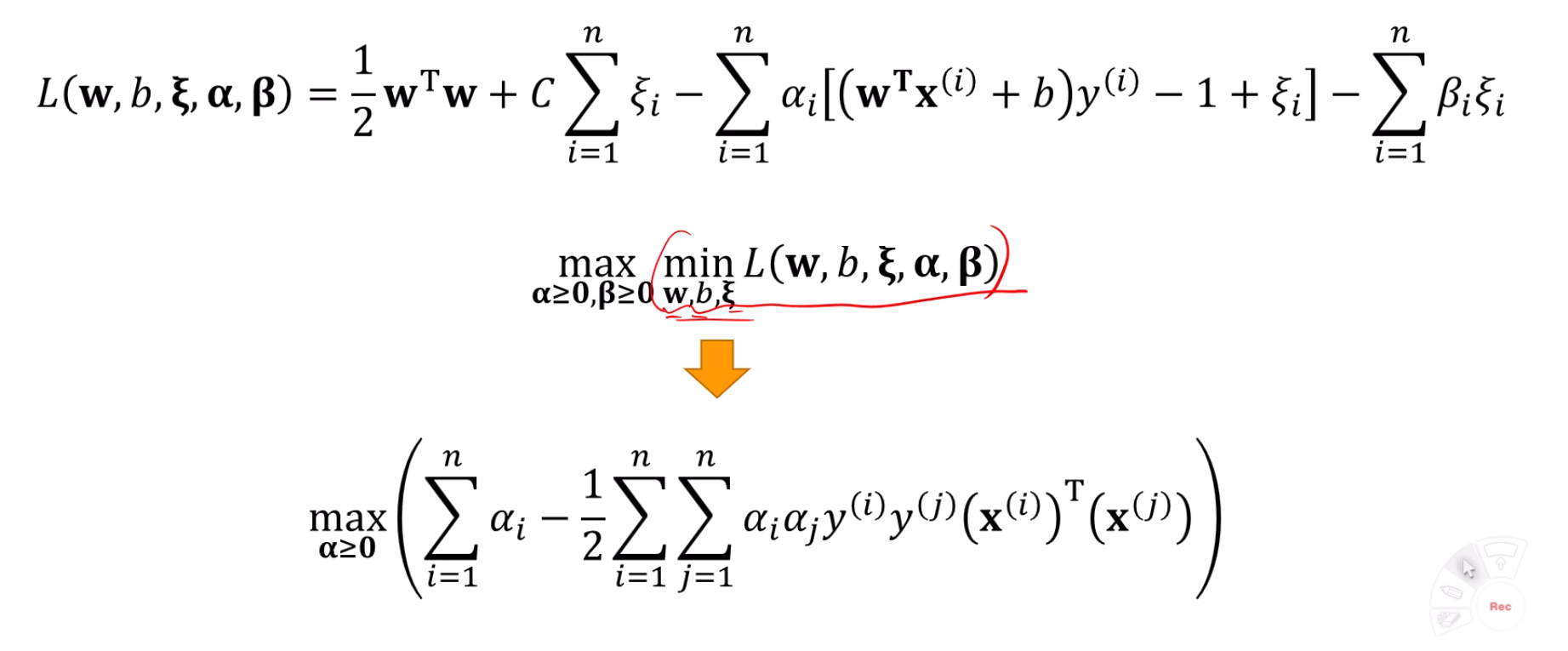
라그랑지안을 w, b, 에 대해 잘 미분을 하면,
놀랍게도 에 대한 식으로 싹 정리가 됩니다.
max는 컴퓨터가 해결
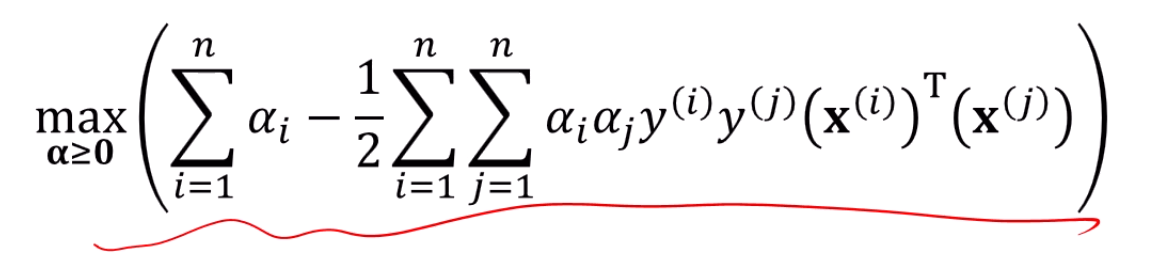
이런 문제는 컴퓨터가 알아서 풀어줍니다.
총 n차원의 가 나오겠죠.
구한 alpha 대입, w / b 얻음
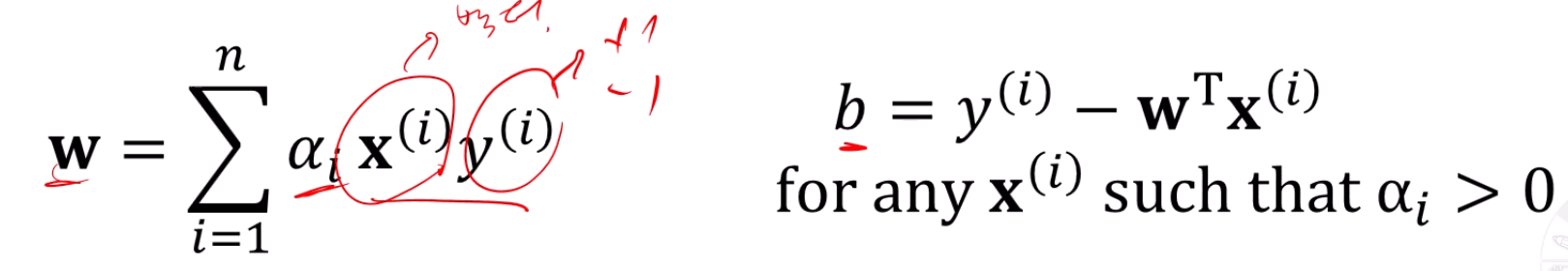
얻은 를 대입하면 w, b가 나옵니다.
정확히는 를 넣어서 w만 구하고, w를 대입해서 b를 구하는거죠.
b에 대입하는 는 Support Vector들 중 아무거나 하나만 넣어주면 됩니다.
아무거나 하나 안 잡고 다 넣어도 똑같은 b만 나옵니다.
짠! 이제 Soft-Margin SVM을 마스터했습니다.
각각의 과정 속의 디테일은 매우 많죠.
이제 '디테일'에 대해 살펴봅시다.
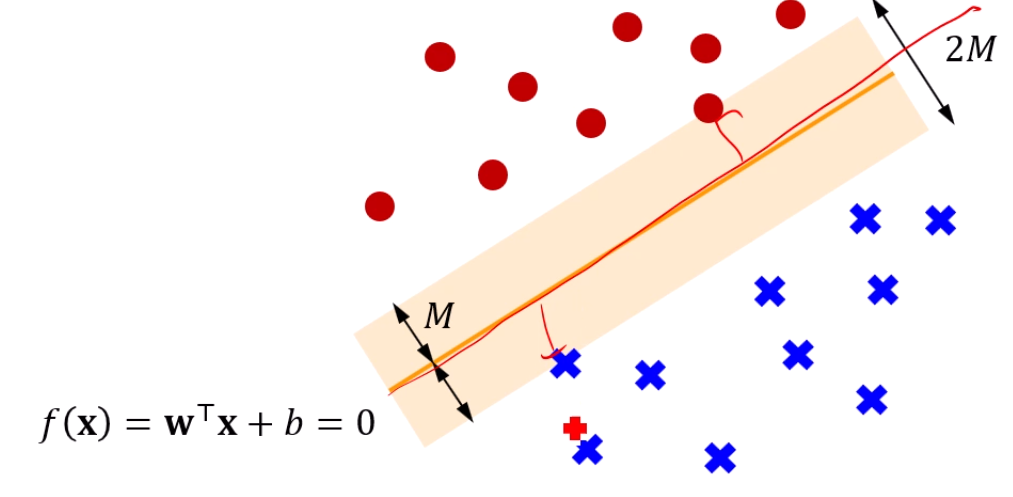
앞서 이 Margin을 maximize하는 초평면을 찾는게 1번째 목표였죠?
Hyperplane과 점과의 거리를 계산을 하고 싶으면,
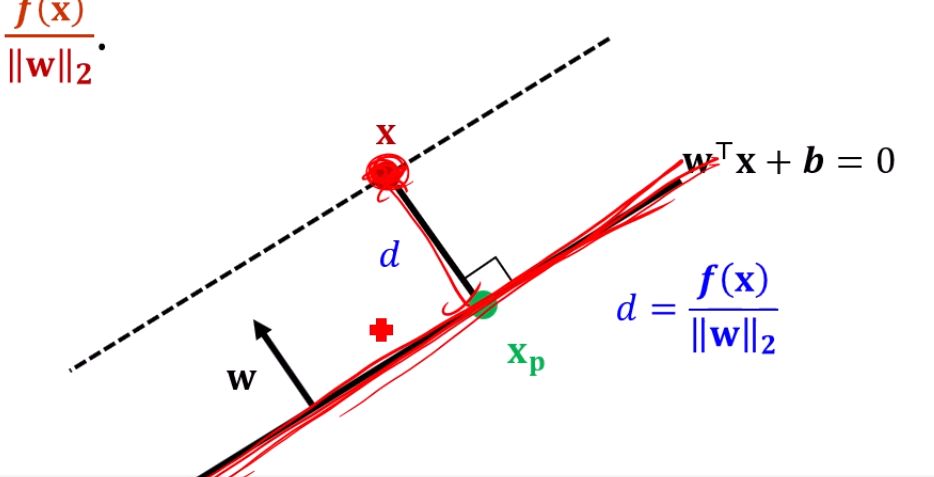
이 를 구하는게 목표인데요,
를 면에 projection 시킨걸 라고 하면,
당연히 이 성립할거구요.
무식하게 에 일단 를 넣어보면,
에서,
가 되고,
앞서 이라고 정의했죠?
즉 만 남게 되며,
임을 이용하면, 가 됩니다.
즉, 가 성립하죠.
초평면과 어떤 점 x와의 거리를 구했습니다.
자.
Dataset 안에 있는 임의의 x에 대해서,
우리는 그 x들과 초평면의 거리가 최소 M은 되기를 바랍니다.
가 되구요.
아까 구한 식을 대입하면
이 됩니다.
또, 초평면의 식에 대입했을 때의 부호를 고려하면,
모든 x에 대해서
이 되기를 기대합니다.
결과적으로 보면,
이라는 제약조건이 있을 때,
을 최대화하는 w, b를 구하는 문제가 됩니다.
여기까진 매우 쉬워요.
근데, w의 크기가 바뀐다손 친들 구해야 하는 정답은 동일하죠?
의 제약을 임의로 지정합시다. 문제는 딱히 없어요.
이 내용을 넣으면, 문제가 이렇게 바뀝니다.
이라는 제약조건이 있을 때,
을 최대화하는 w, b를 구하는 문제가 됩니다.
양변 미분이 되네요? 제약조건이 이렇게 바뀝니다.
또, 을 최대화 하는건 를 최소화하는 문제와 같고,
를 최소화하는건 를 최소화하는 것과 같죠?
그래서,
라는 제약조건 하에서,
를 최소화하는 w,b를 찾는 문제로 바뀝니다.
이 식이 Hard Margin SVM optimization의 기본형태에요!
Soft-Margin SVM
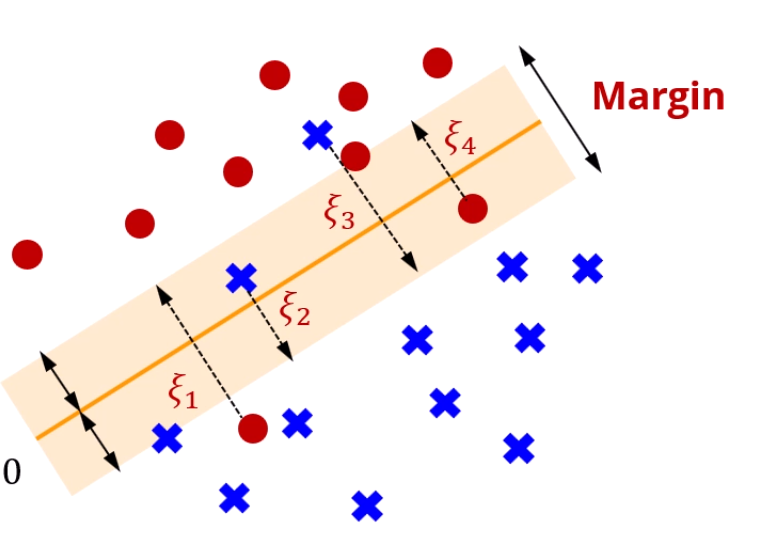
데이터에 오차가 존재하는 경우도 생각을 해야 합니다.
조건을 좀 완화해서, Margin을 최대화를 하긴 하되,
의 합은 최소화 하고자 하는 문제로 바뀝니다.
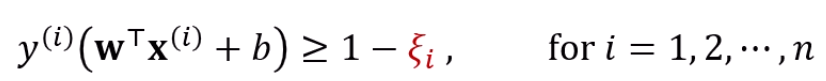
그래서, 원래는 저 제약조건이 1보다 크거나 같으면 됐는데,
이젠 보다 크거나 같으면 되기로 바뀝니다.
대신 그렇다고 를 무한정 키우게는 못하게, 의 합을 최소화하는 조건도 넣습니다.
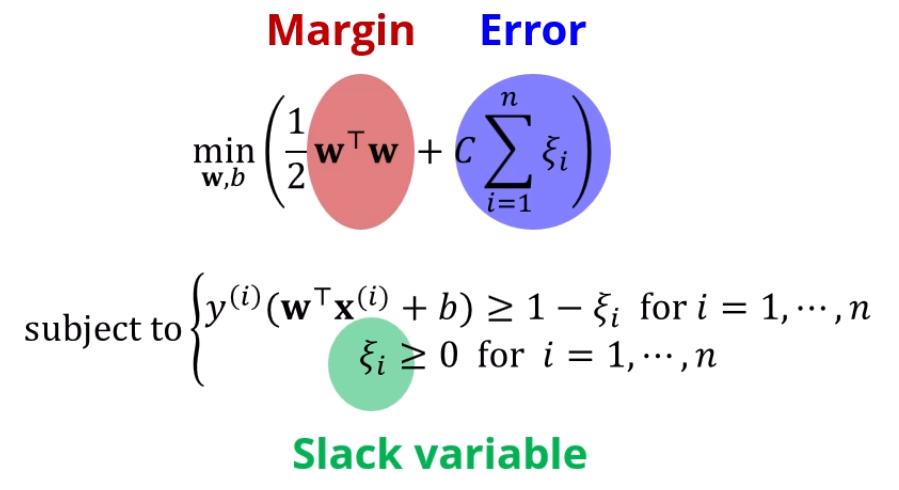
정리를 하면, 기존의 Hard Margin SVM 문제에서,
Error의 합까지 최소화하는 문제로 바뀝니다!
대신 slack variable이 제약조건에 추가가 되구요.
저 C는 margin과 Error 사이에 뭘 더 중점으로 둘지 정하는 상수입니다.
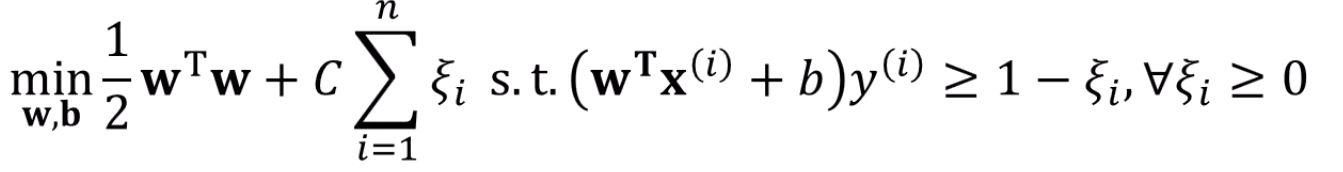
이 문제를 풀 때에는? 라그랑지안을 이용한다~는 점입니다.
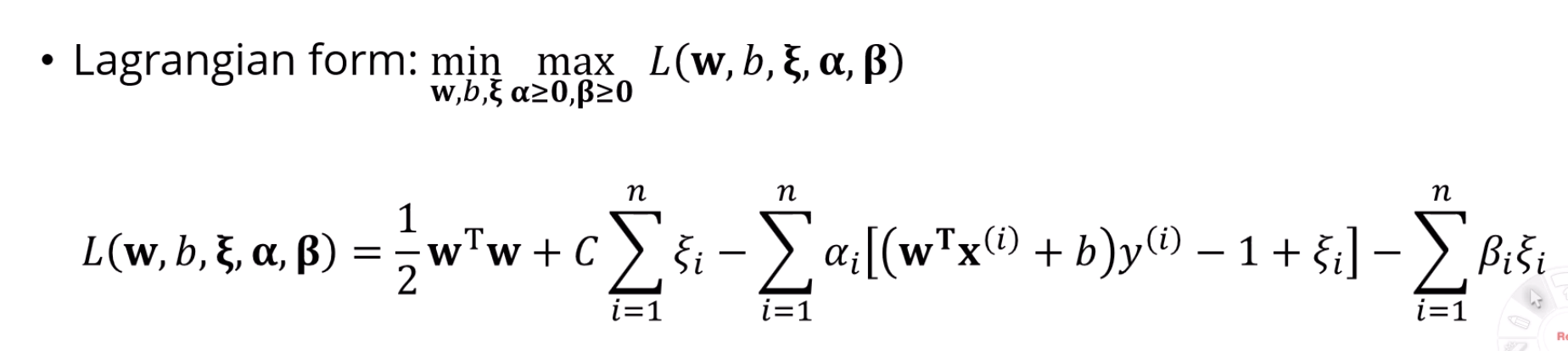
여기서 갑자기 min과 max가 등장하는데, 아 이거 이유가 뭡니까?
결국 '제약조건을 포함한 라그랑지안'을 최소화하는게 목표인데,
그게 되려면 , 를 잘 조합해서,
라그랑지안이 [최대]가 될 수 있는 를 구하되,
그 '최악'의 경우를 최소화시키는 를 찾으면 된다고 이해하면 될 것 같습니다.
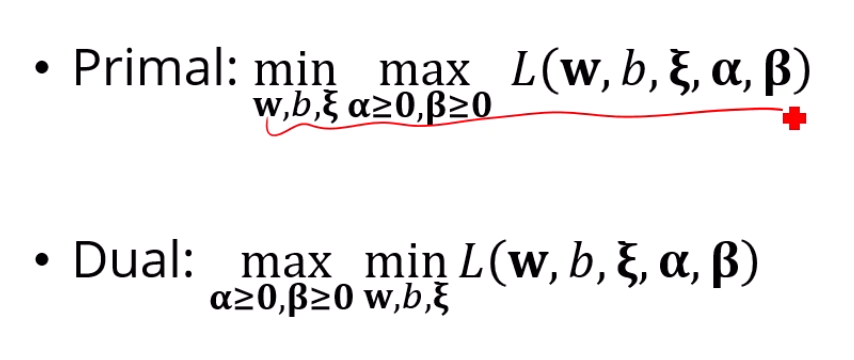
이 문제를 duality를 이용해 max, min을 바꿀 수 있죠?
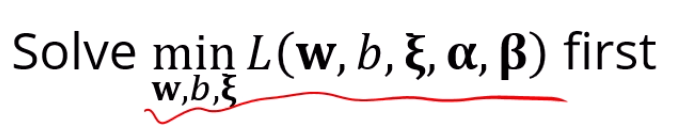
라그랑지안을 최소화하는 문제를 먼저 풀어보는 겁니다.
는 벡터고, 는 스칼라죠.
뭐, 식이 길긴 한데 기본은 미분하는거죠.
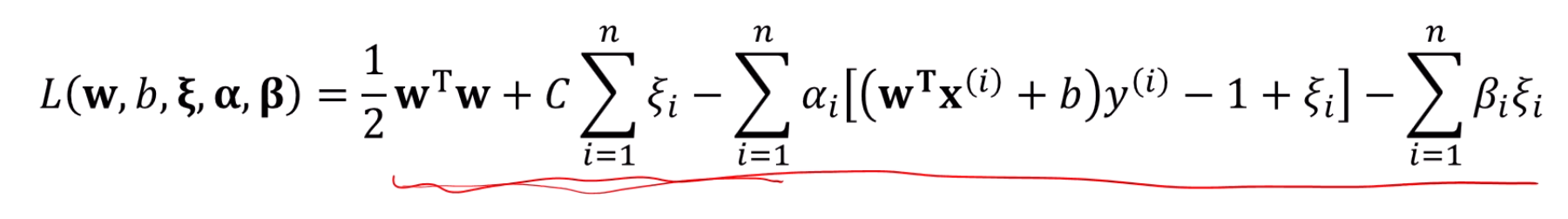
이거 자세히 보면 미분 할만 합니다.
의 미분이 이고, 를 로 미분하면 앞의것만 남죠?
그거 감안하면,
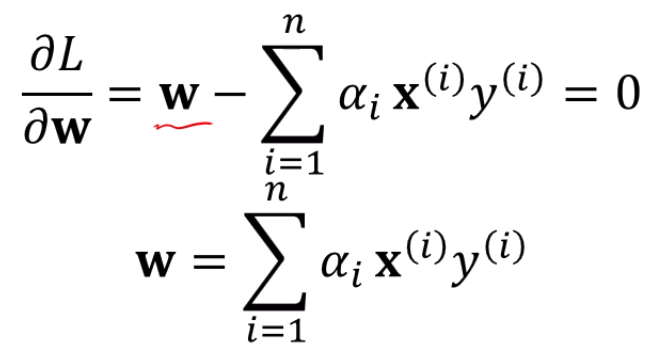
참 쉽게 표현이 되구요.
이렇게 구한 w를 L에 대입할 수도 있습니다.
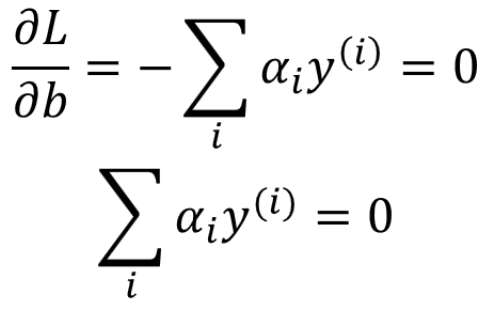
L을 b로 미분하면 제약조건이 하나 더 추가가 됩니다.
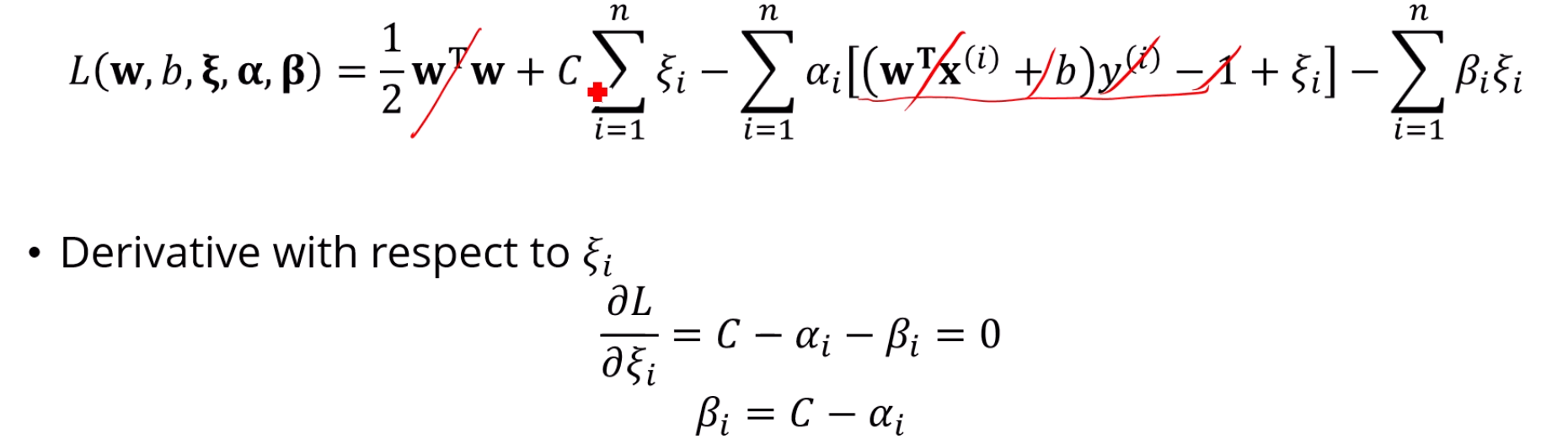
L을 로 미분하면 이 남구요.
이 에 대한 식을 대입해서 를 없애고 보면, 재밌게도 도 같이 사라집니다.
w도, b, 도 없어지니 만 남습니다.
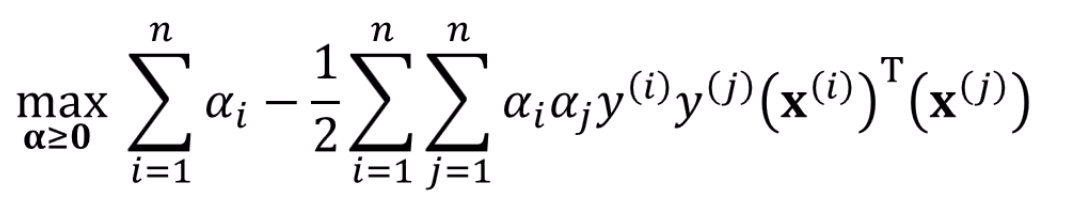
이 식만 남게 돼요.
이건 컴퓨터가 풀어줄거구요.
이게 Soft-Margin SVM입니다!
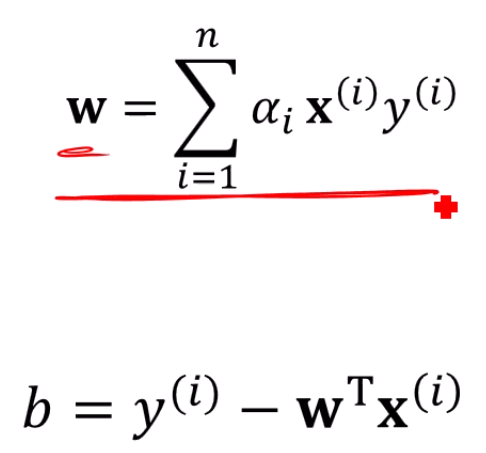
그렇게 구한 를 넣으면, 와 가 나옵니다.
이건 앞선 경우와 같죠.
Kernel Trick (Revisit)
Non-linear SVM을 위해서, 선형적으로 분류가 안 되는 데이터를 차원을 확대시킬 수 있죠.
를 통해 x를 차원을 증가시킬 수 있습니다.
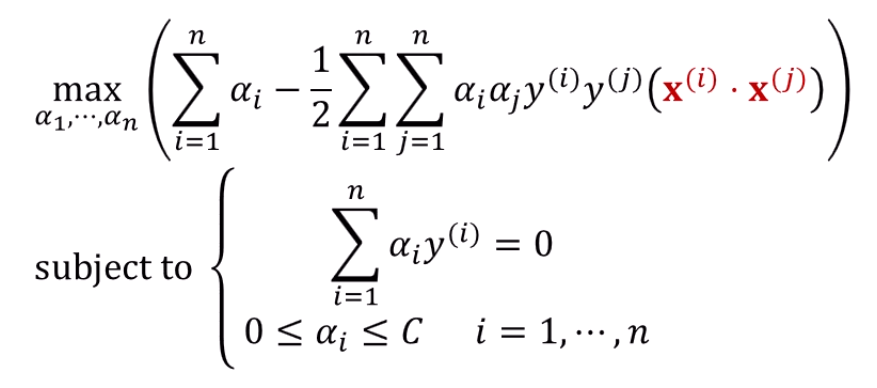
앞서 soft-margin SVM의 식이 다음과 같았는데,
저 를 주목할 필요가 있습니다.
우리가 궁금한건 고차원벡터의 내적을 쉽게 표현하는 방법이 되겠죠.
로 내적이 되어도, 어쨌든 그걸 쉽게 표현만 할 수 있으면 참 좋을테니까요.
그래서 이 값을 라는 새 함수를 이용해 표현합니다.
그리고 SVM에서는 Kernel Function으로 표현을 하면,
의 정확한 값이 얼마인지는 전혀 중요하지 않습니다
대표적인 Kernel Function으로 RBF가 있습니다
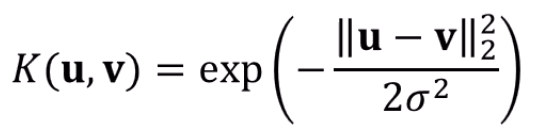
RBF의 장점은, 무한개의 Kernel함수를 합친것처럼 표현이 가능하다는 점입니다.
다르게 말하면 무한차원까지 올릴 수 있다는거죠.

다음 유도를 보면 좋을 것 같습니다.
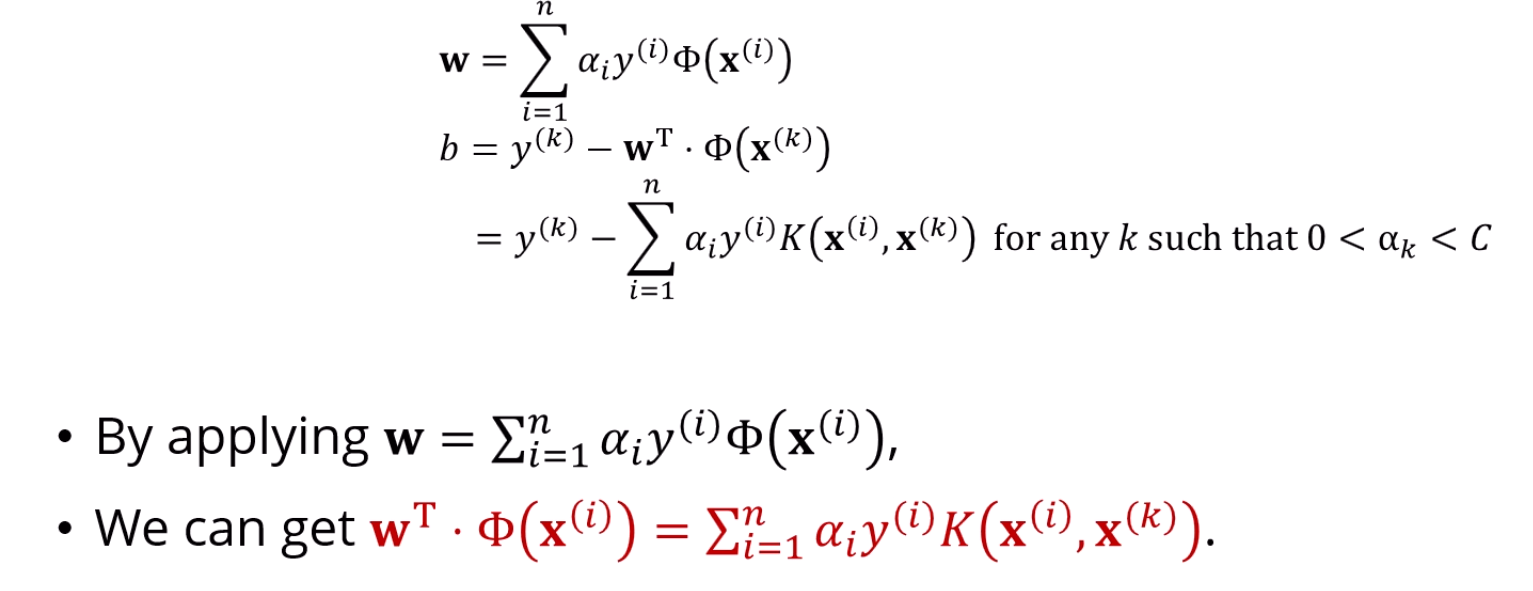
또한, Kernel 함수를 사용하면 b는 Kernel로 표현되는데,
w는 Kernel로 표현이 안 됩니다.
하지만, 결국 구하고자 하는 에 구한 w를 집어 넣으면,
그 곱이 Kernel로 표현이 되기 때문에,
어쨌든 는 쓰이지 않게 됩니다.
