SVM(2)

앞서 min-max 최적화문제를 (primal problem)
max-min 문제로 바꿔 풀어도 된다고 말했습니다.

$||w||_2^2$를 최소화하되, 모든 샘플이 정분류되어야 한다는 조건이 있었습니다.

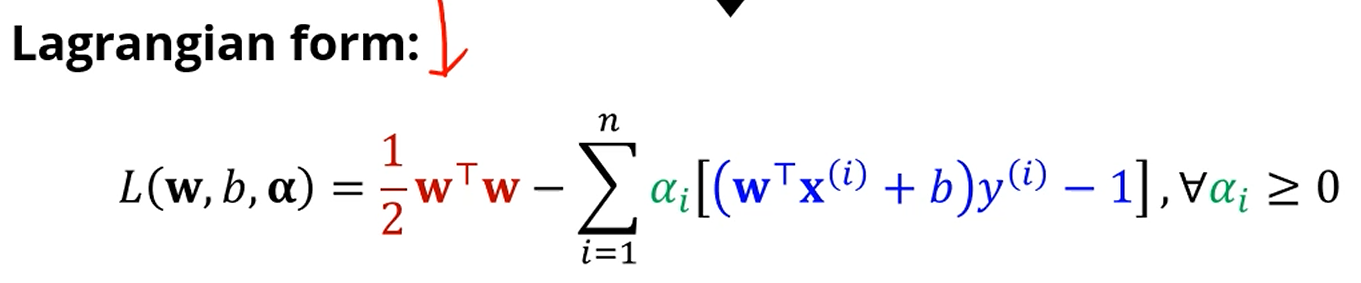
라그랑지안으로 바꾸면 이렇게 되겠죠.
지금은 $\alpha$를 썼는데, 아까는 $\mu$를 썼습니다.
SVM에서는 $\alpha$를 자주 쓰니 $\alpha$를 씁시다.

그래서, 우리가 풀고자 하는 문제는 결국

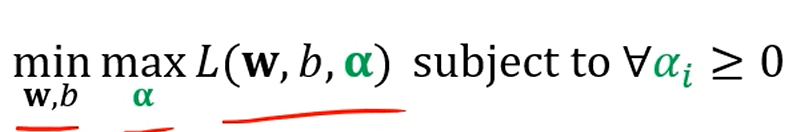
이 문제를 풀고자 하는거죠.

여기서 duality를 적용하면

이런 문제로 바뀌고,
max를 제외한 안쪽 문제만 풀면,
$L(w,b,\alpha)$를 w에 대해 미분하고, b에 대해 미분하면

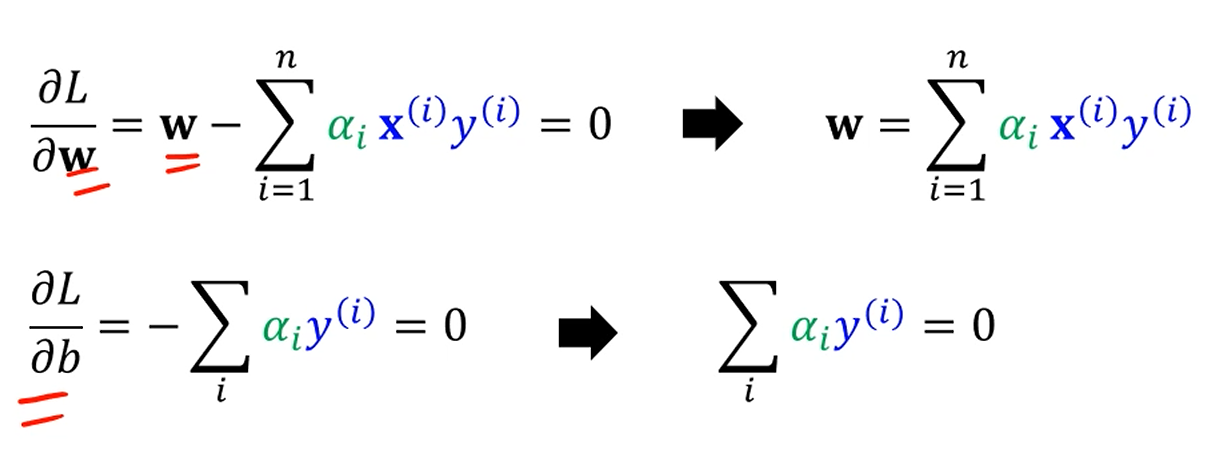
다음같이 미분됩니다.

생각보다 w, b가 쉽게 표현됩니다.

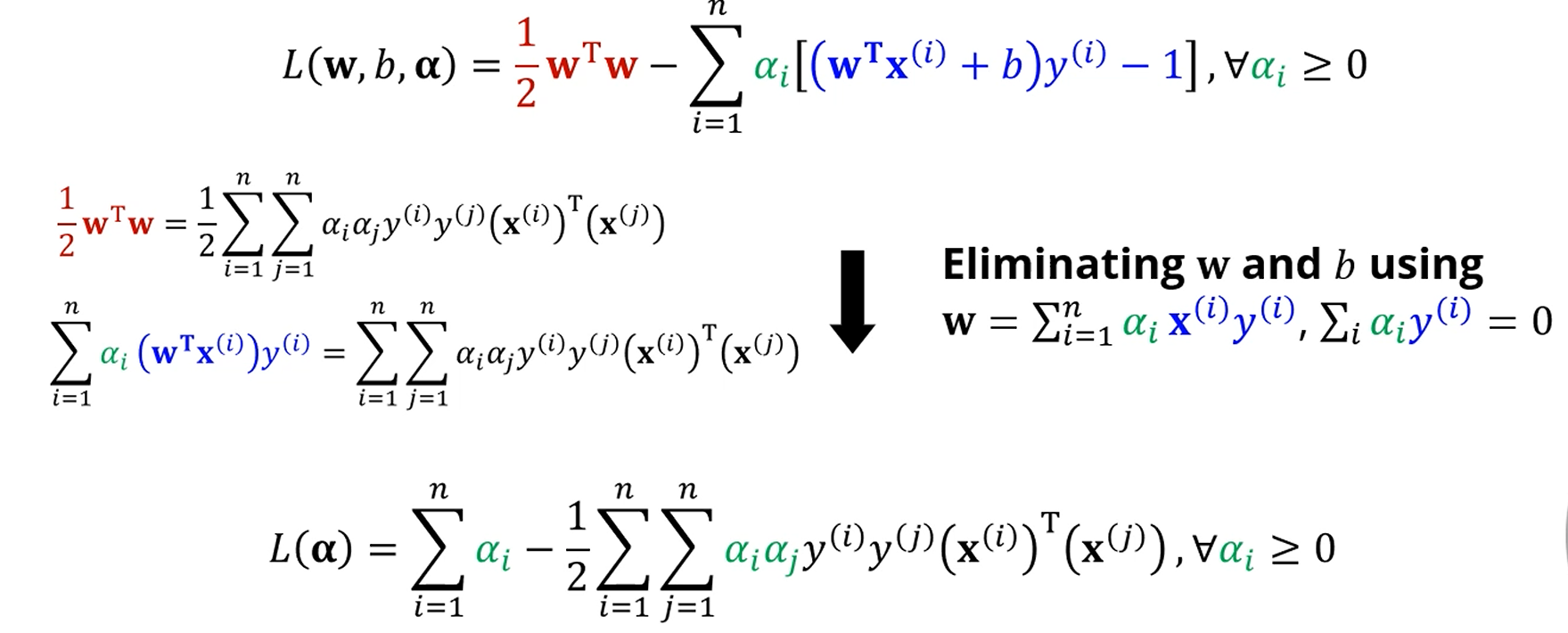
원래 $L(w,b,\alpha)$ 식을 방금 구한 것들을 넣어서 단순화합니다.

이 때, $\alpha_i = 0$이라면, $x_i$는 support vector가 아니게 됩니다.

단순히 대입해서 전개하면 $L(w,b,\alpha)$가 놀랍게도 $L(\alpha)$만 남게 됩니다.

안쪽 식에서 w랑 b가 사라지고 $\alpha$만 남았습니다.
추가적인 constraint가 생기긴 했지만, 그게 뭐가 중요한가요. 변수가 1개가 됐어요.

이 max 문제를 풀었다고 가정합시다.

우린 $\alpha_i$를 다 알고 있습니다.
$\alpha_i$ = 0이면 support vector가 아닌거고, 조금이라도 양수면 $x_i, y_i$는 support vector입니다.

뭐 $w$는 대입하면 구해집니다. 앞에서 $w = \sum \alpha_i x^{(i)} y^{(i)}$가 나왔죠.
b는요?

b는 쓰지 않은 조건들을 이용합니다.

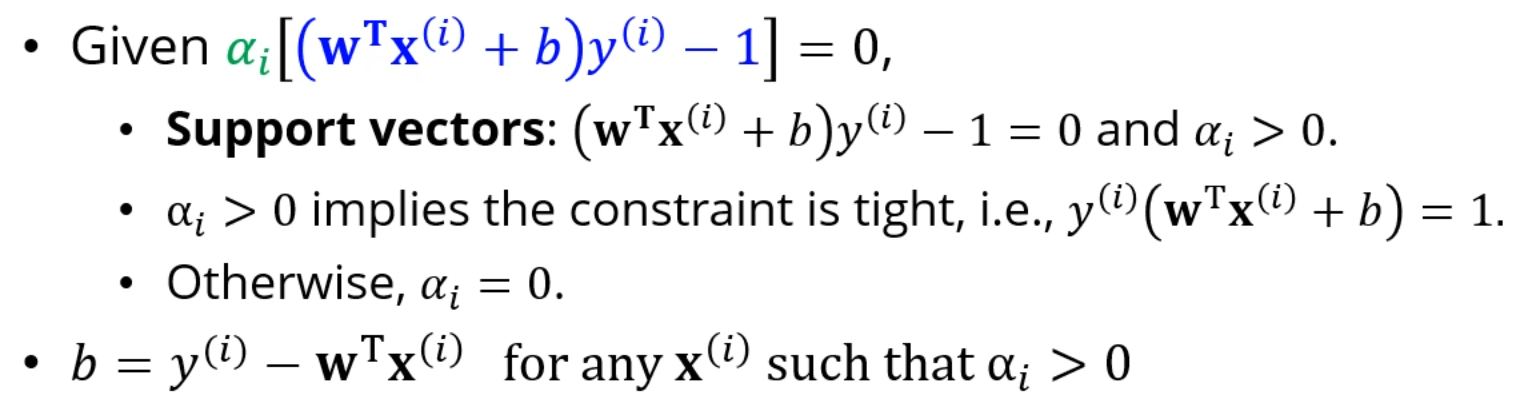
$\alpha_i \neq 0$인 경우만 챙깁니다. $\alpha_i = 0$이라면 support vector가 아니기에 의미가 없습니다.

Summary - Solving Hard-Margin SVM

$\alpha$만 알면 결국 w와 b를 알 수 있다는게 핵심이죠.
$\alpha$는요? 알아서 저 max식을 풀어야겠죠.

그리고 그 $\alpha$는 기계가 구합니다!

$\mathcal{D} = \{(1,1,-1), (2,2,+1)\}$이 있습니다.

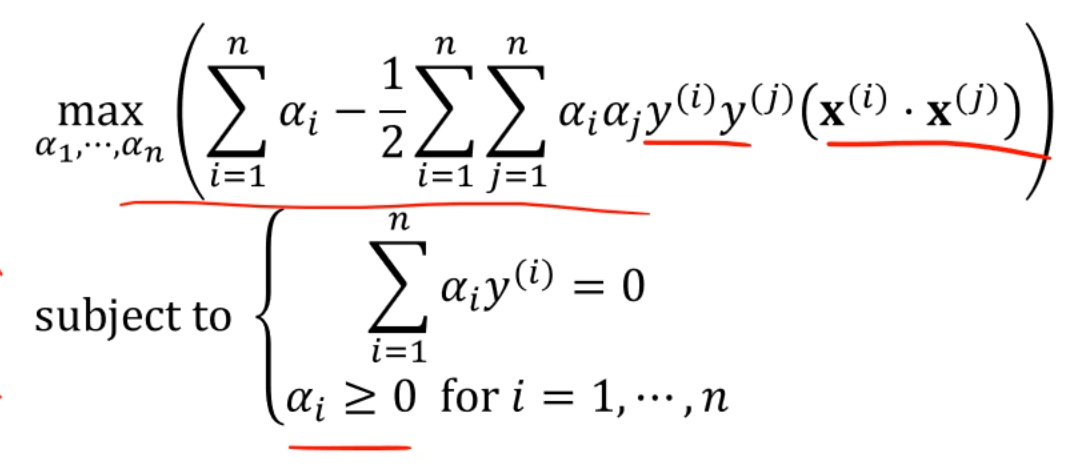
이 식에 x, y를 대입해서 전개를 해줍니다.

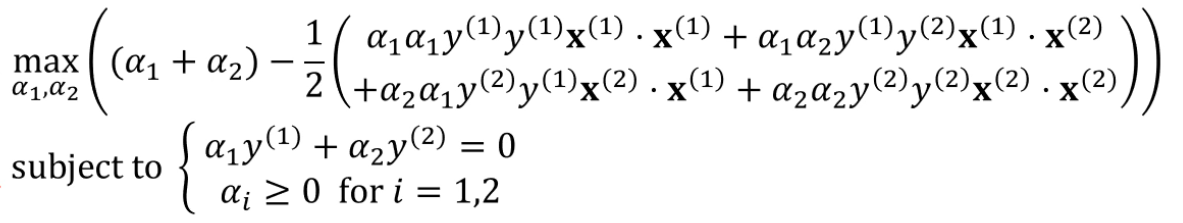
다음 문제로 바뀌었네요.

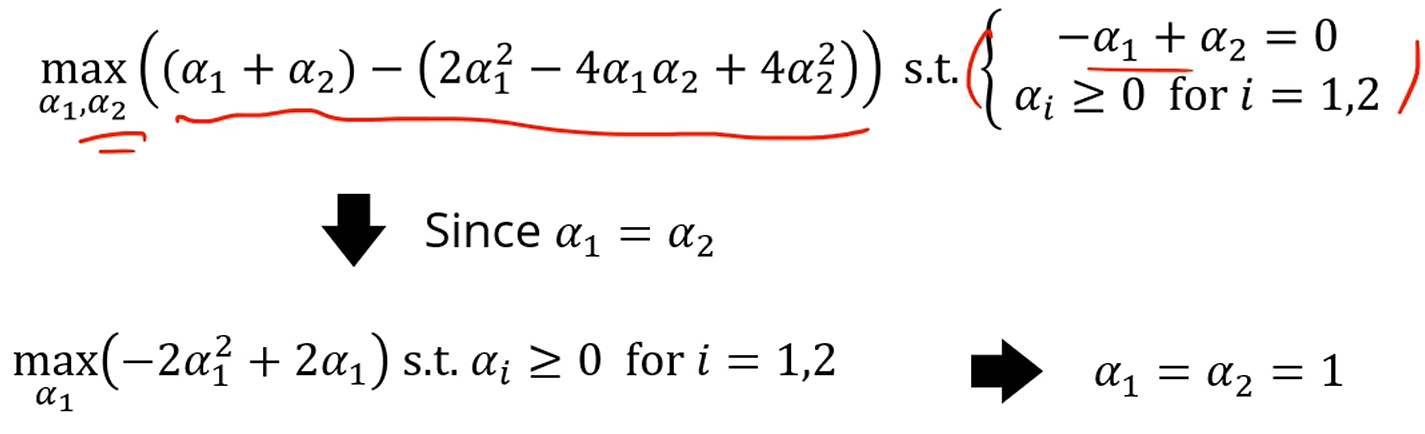
뚝딱뚝딱 전개해보면 다음과 같구요.
$\alpha$를 다 얻을 수 있게 됩니다.

이 경우는 $\alpha_1$, $\alpha_2$ 둘다 양수이니, $x^1, x^2$ 둘 다 support vector네요.

그 후 w랑 b에 대입하면 식을 얻을 수 있죠.

Soft-margin SVM

$\xi$도 포함된 식입니다.
라그랑지안을 적을 수 있구요,

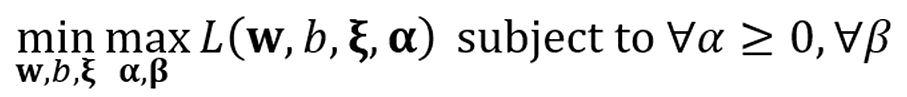
다음과 같은 문제로 치환이 됩니다.
(Duality 아직 적용 안됨.)

저기서 라그랑지안을 $\xi_i$로 미분하면,
$C - \alpha_i - \beta_i = 0$이라는 추가 조건을 얻을 수 있습니다.

이 때, $\beta_i$는 아무리 작아봤자 0입니다.
$\alpha_i = C - \beta_i$이기에 $C \geq \beta_i$가 성립하는데,
$\beta_i$의 최소가 0이니, $\alpha_i$의 최대는 $C$죠.
즉, 일전의 Hard-margin SVM과는 다르게 $0 \leq \alpha_i \leq C$의 조건이 생겼습니다.

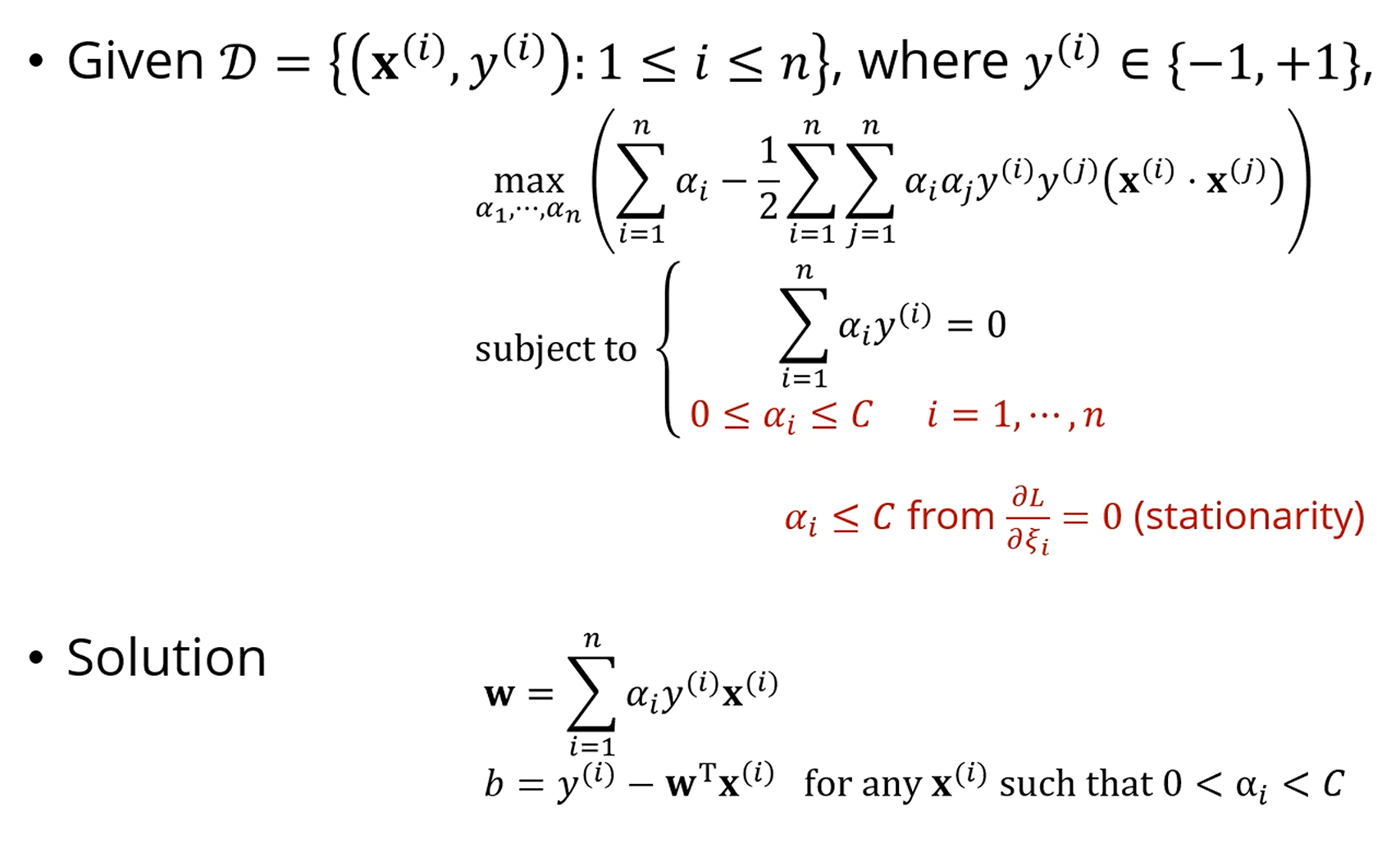
똑같이 간결하게 표현이 됩니다.
역시 $\alpha_i$는 컴퓨터가 구하구요.
대입을 해서 w, b를 얻을 수 있습니다.

Non-linear SVM

결국은 SVM 푸는게 컴퓨터한테 시키는거라면,
Duality는 왜 쓰는거고, 식의 단순화는 왜 하는거고,
Primal problem을 그대로 컴퓨터 주면 되는거 아닌가요?

Duality를 써서 문제를 minmax -> maxmin으로 바꾼다면,
Kernel Trick을 써서 Non-linear SVM을 수행할 수 있게 됩니다.

이거 어떻게 분류해요 ??
noise를 포함해서 그냥 분류한다고 생각해도, 너무 효율이 떨어집니다.
error가 엄청 발생할거에요.

이걸, 차원을 오히려 올려버리면,

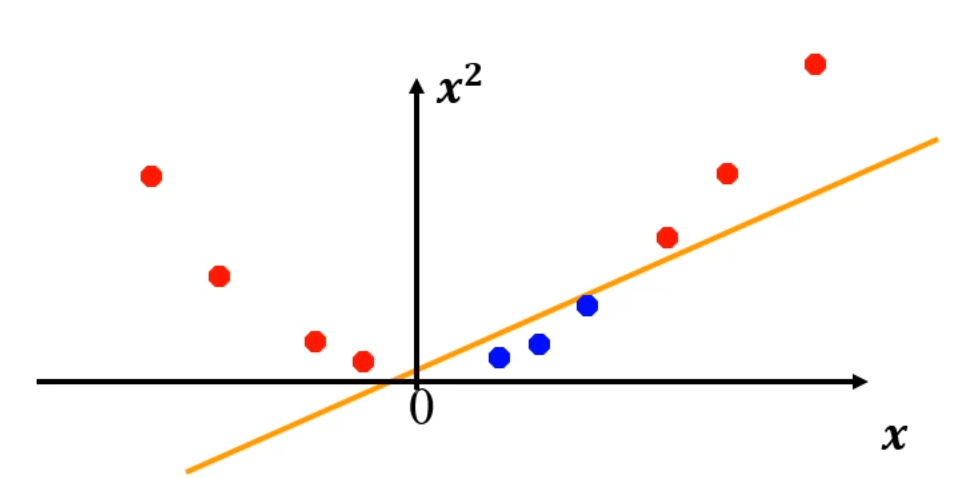
이렇게 하나의 직선으로 분류가 됩니다. 개쩔죠.

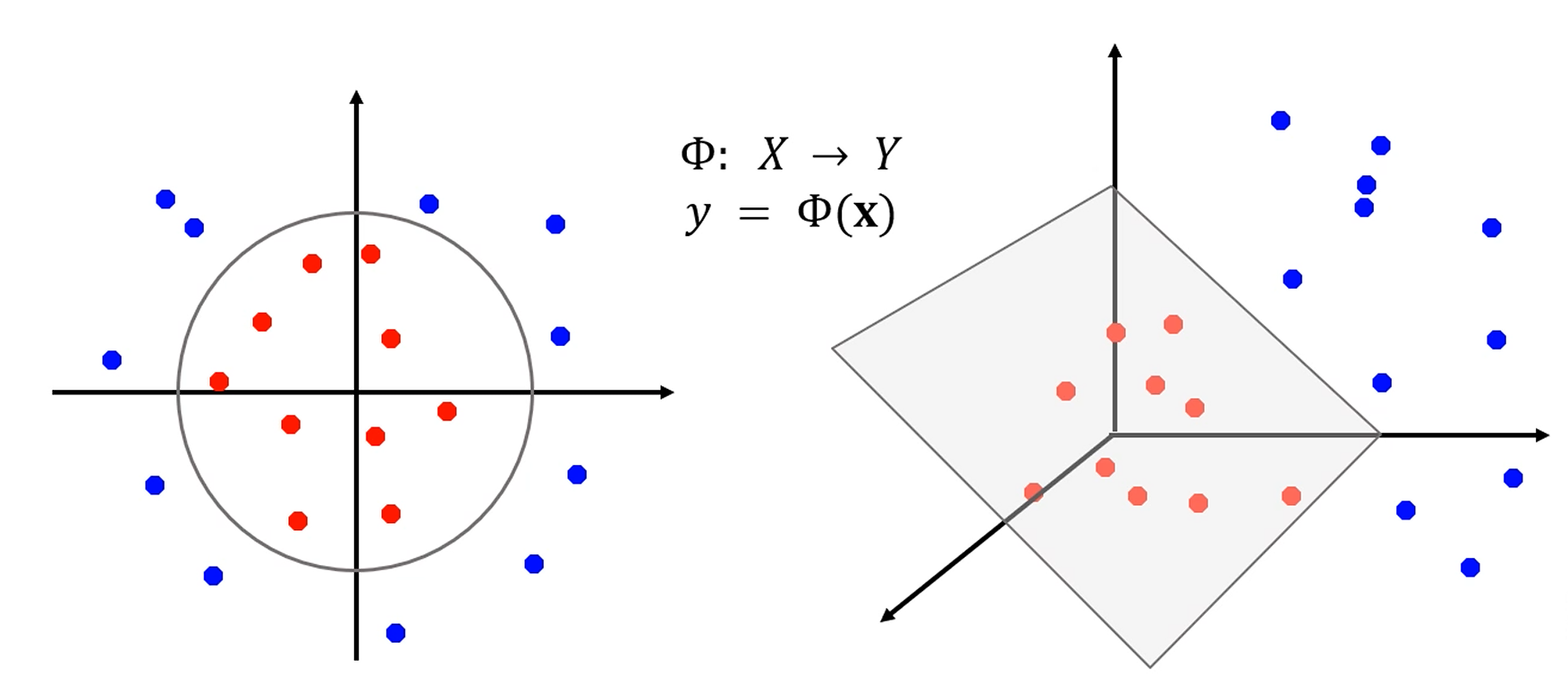
다음과 같이 매핑 함수 $\phi$를 적용하면,
차원을 높여버렸을 때 분류가 가능해지는 경우가 생깁니다.

진심 개쩔죠.

앞서 구했던 SVM의 식입니다.
$x^{(i)}, y^{(i)}$ 다 대입해서 조건을 만족시키는 $\alpha$를 구합니다.
그걸 이용해서 w, b를 구할 수 있었습니다.

차원확대에서는, 저기서 $x^{(i)}$ 대신 $\phi(x^{(i)})$를 쓰면 됩니다.
가령 5차원 대신 10차원 벡터를 쓰는거죠.

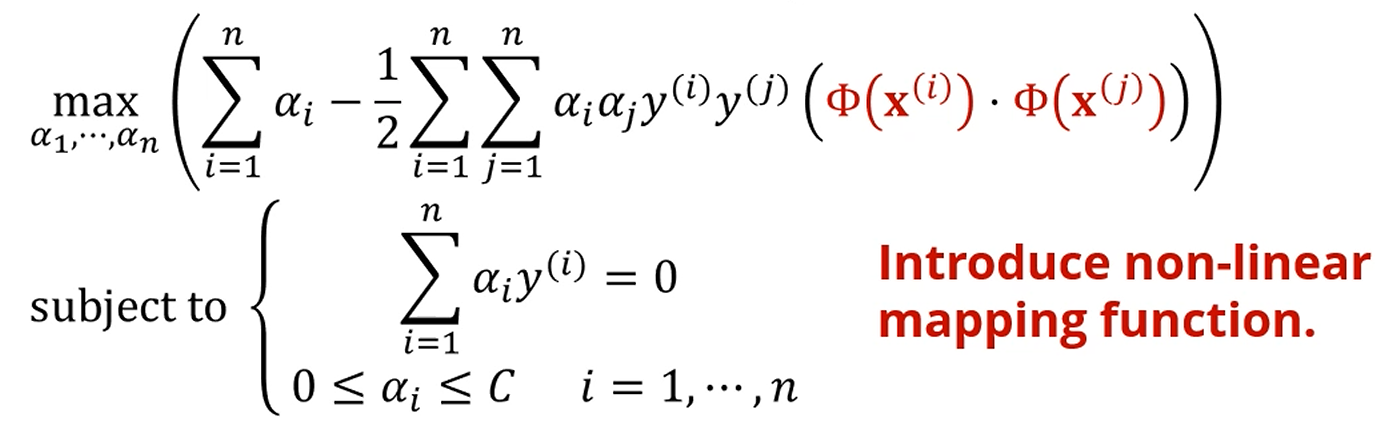
멋지죠.

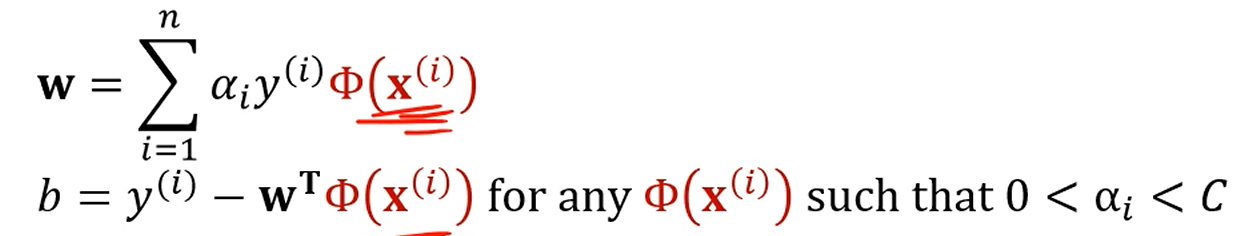
솔루션도 $x(i)$ 대신 $\phi(x(i))$를 쓰면 됩니다.

What is a Kernel Trick?

여기까지만 하면, 새로울게 딱히 없는 차원확대인데요.

원래 데이터가 SVM 문제에 들어갈 때 내적의 형태로만 들어간다는 관찰을 할 수 있습니다.

$x^{(i)}$와 $x^{(j)}$를 $\phi$를 넣어서 매핑해준다고 해도,
SVM 문제에선 결국 $\phi(x^{(i)})\phi(x^{(j)})$만 쓰인다는 겁니다. 다른 연산 없이요.

그래서, 이 연산, $\phi(x_i)\phi(x_j)$를 간단하게 $K(x_i, x_j)$로 쓰기로 한겁니다.

즉, 상위차원으로의 매핑 + 내적까지 한번에 해주는 함수가 Kernel Function입니다.

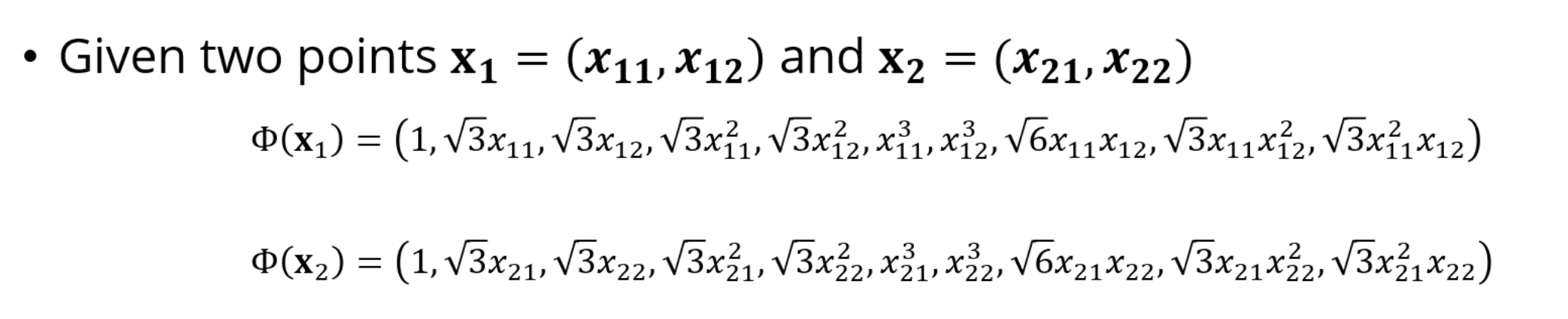
우리가 $\phi$를 이렇게 정의해서, 2차원을 9차원으로 매핑시킨다고 해봅시다.
뭔가,, 못생겼죠.

근데 놀랍게도

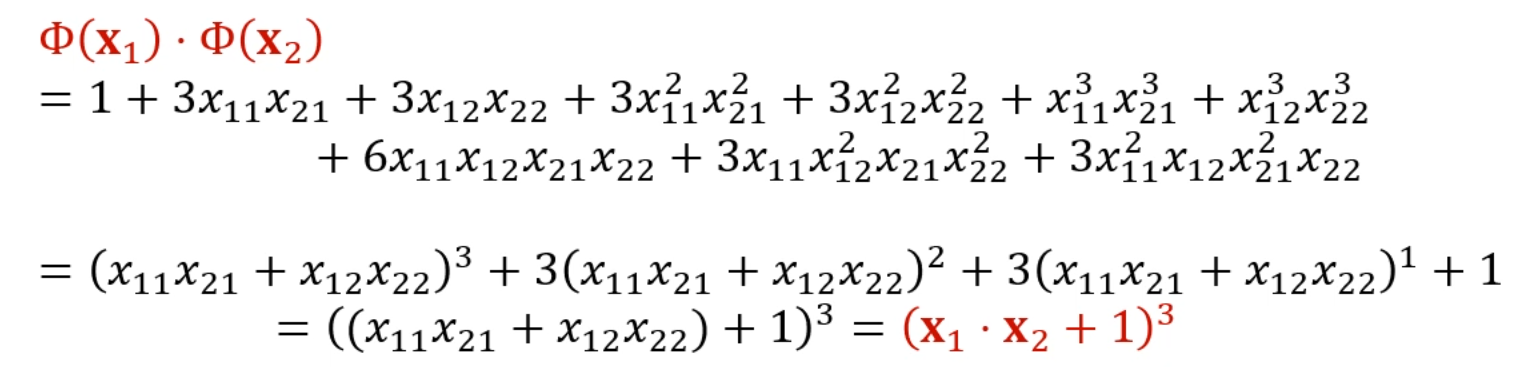
둘을 내적하면? 정말 이쁜 결과가 나옵니다.

즉, 매핑 함수를 잘 짜면, 내적의 결과가 매우 깔끔하게 정리가 된다는 것입니다.

거추장스러운 매핑 과정
+
거추장스러운 내적 과정

=
정말 이쁜 완성된 식이 된다는 거에요.

이러한 것을 Kernel Trick이라고 부릅니다.

고차원으로 올린 후 내적하는걸,
저차원상에서 간단한 내적하고 연산만 좀 추가한걸로 바꿨으니까요.

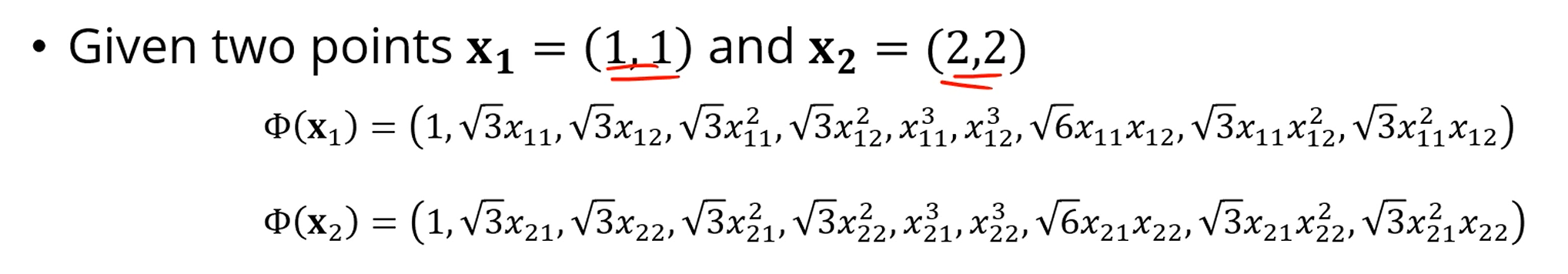
이걸 Kernel Trick 없이 직접 구하면,
저거 다 내적해야합니다.

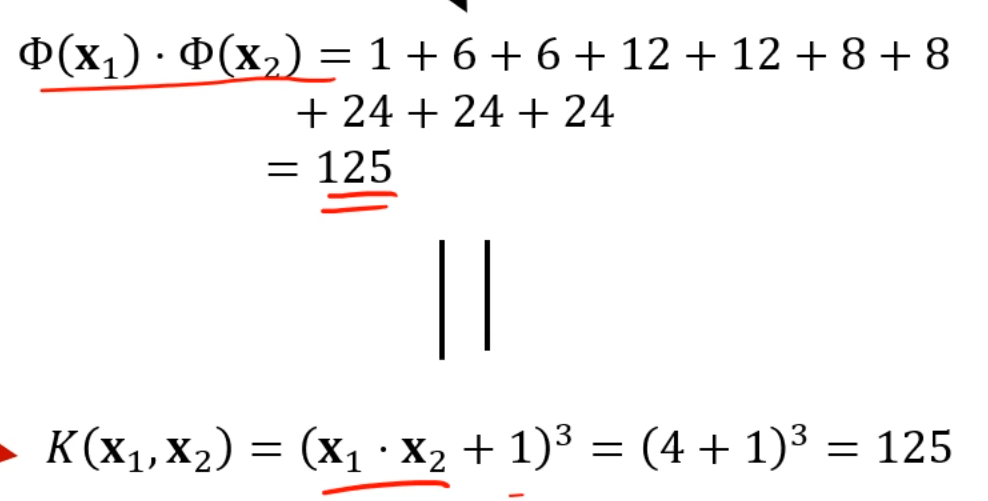
근데, 무식하게 내적하는것하고 커널 함수에 넣어서 딸깍 하는것과 결과가 같게 나옵니다.

이 얼마나 좋습니까.

Common Kernels

두개의 벡터가 주어졌을 때, 두 벡터의 관련성을 나타낼 수 있는 어떤 함수도 괜찮습니다.

대신, 내적이니까 비슷한 값들은 큰 값이 나오고
비슷하지 않은 값들은 작은 값으로 나오는게 맞습니다.

$K(u,v) = (u v)^d$로 나타낼 수도 있습니다.

그럼 실제 $\phi$는 뭐냐구요? 그건 몰라요. 궁금하지 않아요.

아니면 $K(u,v) = (uv+1)^d$로 나타낼 수도 있겠네요.

혹은 Radial Basis Function (RBF) 커널을 쓸수도 있습니다.

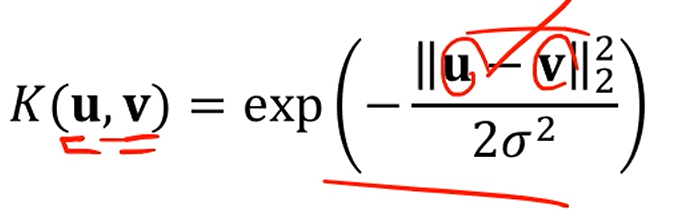
RBF Kernel

$\sigma^2 = 1$로 둡시다.

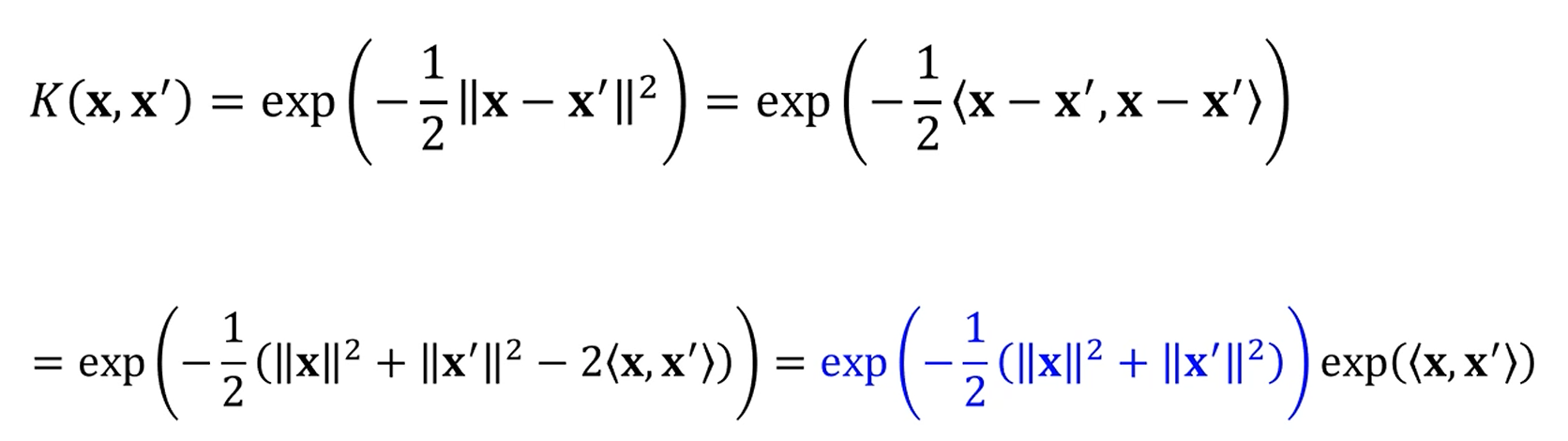
이 때 저 파란색을 C라는 상수로 대체하면,
$K(x,x') = Ce^{xx'}$가 되는데,
$e^x$를 테일러전개를 할 수 있죠? 이걸 저 exp 항에 통으로 씌우면,

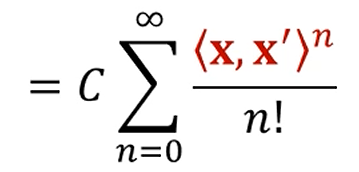
짠
다음과 같이 됩니다.

n차 polynomial kernel을 무한급수를 취한 형태로 변환이 되는 이점이 있습니다.
(이게 왜 이점인지는 모르겠네요)

Formulating Non-linear SVM

이렇게 차원확대를 하되,
$\phi$를 다음과 같이 잡으면 Kernel function이 이쁘게 만들어집니다.

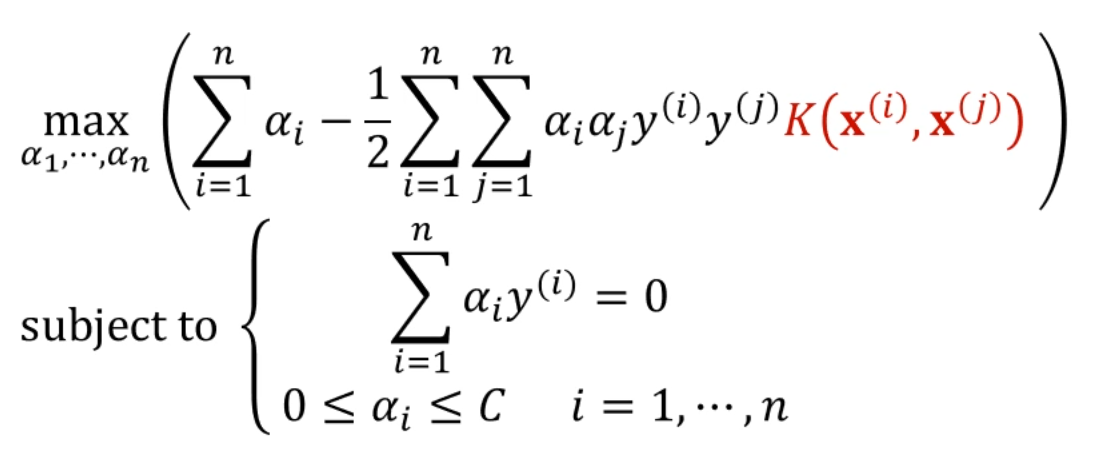
그럼, Kernel Function이 적용되었을 때 w랑 b는 어떻게 바뀌어야 할까요?

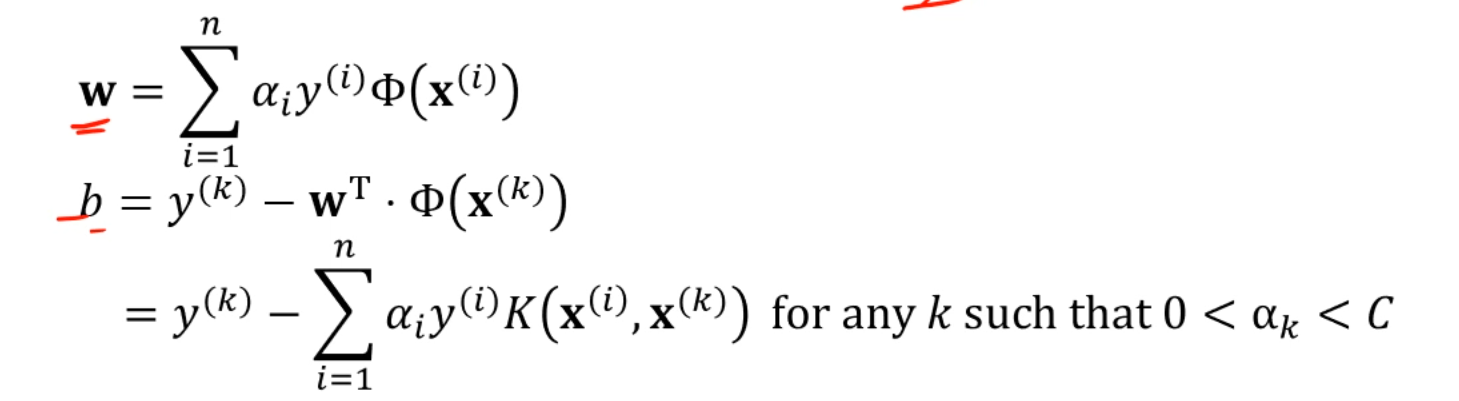
w야 뭐 그대로 차원확대된 대로 쓰면 되지만,
b는 w를 대입해서 전개하면, Kernel Function으로 전개가 가능해집니다.

엥.

근데 우린 $\phi$ 없이 $K$만으로도 다 끝내고 싶었는데요.
w를 구하려면 결국 $\phi$를 알아야 하네요.

그런데.

SVM으로 '분류'를 하고자 한다면 w를 굳이 알 필요는 없습니다.

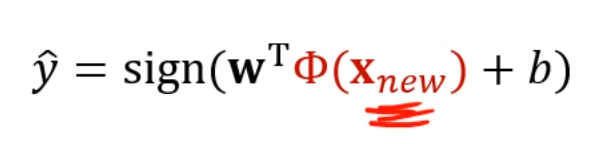
$x_{new}$를 SVM을 통해 분류하려면,
차원확대 한 후, 초평면 식에 넣어서 부호를 알아야 하는 것인데,
그럼 w를 알아야 하는 거 아닌가요?

앞서 구한 w를 넣고, $\phi(x_{new})$까지 고려하면, 놀랍게도 둘이 곱해져서 Kernel Function의 형태가 됩니다.

이야, Kernel Trick을 쓰는 이유가 있네요.

$\phi$가 어떻게 되든 그건 중요하지 않습니다.
결국 w랑 b를 구할 때에는 우리가 정의한 Kernel Function만 쓰이는거에요.

K만 잘 정하면, 차원확대의 효과를 실제로 고차원으로 데이터를 보내지 않고도
'분류'는 수행할 수 있게 됩니다.

물론 뭐 정확한 값을 원한다면 $\phi$는 알아야겠죠.

Summary - Kernel SVM

Kernel Function을 고르되, RBF Kernel이 자주 사용되구,

C (Slack Penalty)도 정해야 하고,

거기서 찾아야 하는 $\alpha$는 컴퓨터가 찾아준다.