[Network Science]3. Random Graphs

YongUk·2025년 1월 24일
GNNGraphnetwork science

Graph Theory

목록 보기
5/17

Random Graph

G(n,m) model

  • n개의 노드와 m개의 edge로 이루어져 있다.

  • 여러 가능한 경우의 수 중 하나를 랜덤으로 선택

G(n,p) model

  • n개의 노드와 p의 확률로 연결되는 edge들을 가진다

  • 고정된 edge의 개수가 없기 때문에 조금 더 다양한 유형의 그래프를 만들 수 있음

  • ⟨m⟩=pn(n−1)2\langle m \rangle = p\frac{n(n-1)}{2}

    • 생성되는 edge의 평균 개수

  • ⟨k⟩=1n∑iki=2⟨m⟩n=p(n−1)≈pn\langle k \rangle = \frac{1}{n}\sum_ik_i = \frac{2\langle m \rangle}{n} = p(n-1) \approx pn

    • 평균 degree

  • P(m)=(Nm)pm(1−p)N−mP(m) = \binom{N}{m}p^m(1-p)^{N-m} (N=n(n−1)2)(N=\frac{n(n-1)}{2})

    • 전체 그래프에서 생성되는 edge의 확률 분포

  • P(ki=k)=P(k)=(n−1k)pk(1−p)n−1−kP(k_i = k) = P(k) = \binom{n-1}{k}p^k(1-p)^{n-1-k}

    • 특정 노드의 degree의 확률 분포

G(n,p) model 포아송 근사

  • 이항분포에서 n이 크고 p가 작다면 포아송 분포를 따른다. 이를 그래프에 적용시키면 노드의 수가 충분히 많고 sparse한 그래프는 포아송 분포를 따른다고 말할 수 있다.
p(k)=λke−λk!     λ=pn=⟨k⟩p(k) = \frac{\lambda^ke^{-\lambda}}{k!} \ \ \ \ \ \lambda = pn = \langle k \rangle

Largest Connected Component

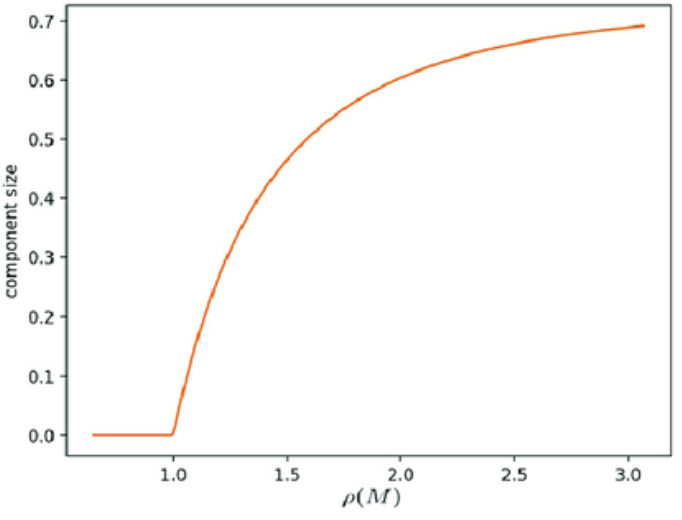
  • p가 0일 때 연결요소는 없을 것이고 p가 1일 때는 모든 가능한 edge가 연결되어 있을 것이다. p를 0에서 1로 서서히 증가시키면 어느 시점에서는 거대한 연결 요소를 발견할 수 있다.
  • 이를 상전이라고 말한다 (혹은 상태 변화)

Phase Transition

u=n−nGn=P(k=0)+P(k=1)×u+P(k=2)×u2+...u = \frac{n-n_G}{n} = P(k=0) + P(k=1)\times u + P(k=2) \times u^2+...
=∑k=0∞P(k)uk=∑k=0∞λke−λk!uk=e−λeλu=eλ(u−1)= \sum_{k=0}^\infin P(k)u^k = \sum_{k=0}^\infin \frac{\lambda^ke^-\lambda}{k!}u^k = e^{-\lambda}e^{\lambda u} = e^{\lambda (u-1)}
  • 공식을 간단히 설명하면 u는 거대 연결요소에 연결되지 않은 노드의 비율 혹은 않을 확률이라고 생각하면된다
  • 또한 이 확률은 특정노드가 k개 이웃들과 연결되어있을 때 그 k개의 이웃들이 모두 거대 연결요소와 연결되어있지 않을 확률들을 구하는 것이다.
  • 이 식을 마지막에 테일러 급수를 이용하여 정리할 수 있다.
u=eλ(u−1)/  s=1−uu = e^{\lambda(u-1)} / \ \ s = 1 -u
1−s=e−λs1-s = e^{-\lambda s}
s=1−e−λss = 1 - e^{-\lambda s}
  • s는 거대 연결 요소에 포함된 노드들의 비율로 나타낼 수 있다. 이와 같은 공식을 도출해내도 푸는 것은 어렵기에 좌표평면 상에서 분석을 해보도록 하겠다. s와 1−eλs1-e^{\lambda s}의 교점을 구하여 해결할 수 있다.

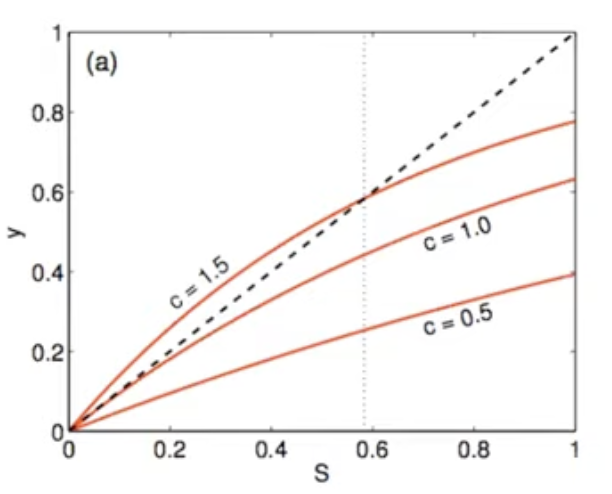
  • λ←0\lambda \larr 0 일 때 s는 0이 되고 λ←∞\lambda \larr \infin 일 때 s는 1이 된다. λ\lambda가 커짐에 따라 s는 0에서 시작하며 일정 임계치를 넘으면 거대 연결요소가 출현하게 된다. 이 때 출현하는 위치는 이 두 그래프의 교점이 1개에서(0) 2개로 늘어나는 시점이고 두 식이 접하는 지점이 될 것이다.
1<λe−λs1 <\lambda e^{-\lambda s}
  • 이 때 s = 0에서의 그레디언트가 1보다 커지는 시점은 λ>1\lambda > 1 인 시점이다.
  • 즉 상변이가 일어나는 임계치는 λc=1\lambda_c =1이고 다시 말하면 ⟨k⟩=1\langle k \rangle = 1 인 시점이 된다. 혹은 pc=1np_c = \frac{1}{n}인 시점이라고 할 수 있다.

Properties of Random Graph

Node Degree Distribution

p(k)=λke−λk!     λ=pn=⟨k⟩p(k) = \frac{\lambda^ke^{-\lambda}}{k!} \ \ \ \ \ \lambda = pn = \langle k \rangle
  • 우리가 일반적으로 알고 있는 Power Law Distribution이 아닌 Poisson Distribution을 만족한다

Clustering Coefficient

Ci(k)=pk(k−1)/2k(k−1)/2=p=⟨k⟩nC_i(k) = \frac{pk(k-1)/2}{k(k-1)/2} = p = \frac{\langle k \rangle}{n}
  • n이 커지면 C가 굉장히 작아지기 때문에 클러스터링 계수가 높지 않다. 따라서 랜덤 그래프에서는 군집성을 만족하지 않는다.

Graph diameter(small world)

n=1+⟨k⟩+⟨k⟩2+...⟨k⟩D=⟨k⟩D+1−1⟨k⟩−1≈⟨k⟩Dn = 1 + \langle k \rangle + \langle k \rangle^2 + ... \langle k \rangle^D = \frac{\langle k \rangle ^{D+1} -1}{\langle k \rangle - 1} \approx \langle k \rangle ^D
D≈ln⁡nln⁡⟨k⟩D \approx \frac{\ln n}{\ln \langle k \rangle}
  • 로그 스케일로 변환이 가능하기 때문에 일반적으로 small world라고 표현할 수 있다.
  • G(n,p) Random Model이 실제 그래프의 성질 중 유일하게 만족하는 특성에 해당한다.

Configuration Model

  • 위 모델은 각 노드의 degree를 미리 정해놓는 모델이다.

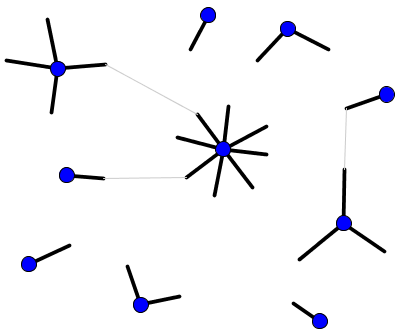
  • 위와 같이 이미 정해진 degree에 서로 연결을 시키기만 하면되는 모델이 될 것이다.
pij=kikj2m−1p_{ij} = \frac{k_ik_j}{2m-1}
  • 이때 서로 다른 두 노드가 연결될 확률은 다음과 같이 나타낼 수 있고 이때 self loop를 형성하거나 multiple edge도 가질 수 있음을 암시한다.
profile
YongUk
이전 포스트

[Network Science]2. Power Law and Scale-free networks

다음 포스트

[Network Science]4. Network Models

0개의 댓글