[Network Science]10. Epidemics on Networks 2

YongUk·2025년 2월 13일

GNN Graph network science

Graph Theory

목록 보기

12/17

part 1에서 본 모델은 우리가 한 노드에서 다른 노드로 무작위로 전파가 가능하다는 가정을 하고 진행하였다.
part 2에서는 실제 네트워크의 동작과 유사하게 서로의 이웃 간의 전파만 가능하도록 하는 모델과 그의 logic에 대해서 학습할 수 있다.
여기서 각각의 노드의 status를 다르게 정의해야한다. 추가적으로 특정 노드에 대한 information도 추가 해야한다. 따라서 기존의 변수들을 다음과 같이 정의할 수 있다.

s(t) = s_i(t) \ \ \ , \ \ \ i(t) = x_i(t) \ \ \ , \ \ \ r(t) = r_i(t)

timestamp t에 따른 node i의 status를 의미한다.

Probabilistic Model’s Two Process

Infection

P_{infection} \approx \beta s_i(t) \sum_{k \in N(i)} x_k(t) \delta t

$\beta$ : 한 노드에서 다른 노드로 감염시킬 수 있는 확률
$s_i(t) :$ t시간에 i 노드가 비감염노드일 확률
$x_k(t)$ : i노드의 이웃 노드이 감염될 확률ㅇ 합으로 $\beta$ 에 곱해지며 이웃이 많은 노드일 수록 감염확률이 높아진다.

Recovery

P_{recovery} = \gamma x_i(t)\delta t

노드 i가 감염되었을 때의 확률에 $\gamma$ (회복률)을 곱하여 간단하게 정의할 수 있다.

Epidemic model

SI model

Mathematical

x_i(t+\delta t) = x_i(t) + \beta s_i(t)\sum_jA_{ij}x_j(t)\delta t

이때 계산의 편의성을 위해 neigher를 인접행렬의 형태로 변환시킬 수 있고 t시점의 확률에 확률 + 시간 변화량에 따른 확률로 표현할 수 있다.
이전에 분석한 것과 비슷하게 미분방정식을 유도해본다

\frac{dx_i(t)}{dt} = \beta s_i(t)\sum_jA_{ij}x_j(t)

x_i(t) + s_i(t) = 1

\frac{dx_i(t)}{dt} = \beta (1-x_i(t))\sum_jA_{ij}x_j(t)

이전에 배운 것을 통해 위 식까지 정리가 가능하다. 이때 $t \rarr 0$ 일 때 $x_i(t)$ 는 일반적으로 낮은 값임을 기대하여 위 식은 다음과 같이 수정한다.

\frac{dx_i(t)}{dt} = \beta \sum_jA_{ij}x_j(t)

위에 유도한 식을 행렬의 형태로 간단히 정리할 수 있다.

\frac{dx(t)}{dt} = \beta Ax(t)

이 문제를 eigenvector를 이용하여 구할 수 있다. $Av_k = \lambda_kv_k \\x(t) = \sum_ka_k(t)v_k$
위에서 eigenvector를 이용하여 x(t)값을 구할 수 있고 이를 원래 식에 대입하여 풀면

\frac{da_k(t)}{dt} = \beta\lambda_ka_k(t)

이 미분방정식을 풀게되면 다음과 같다 $a_k(t) = a_k(0)e^{\beta\lambda_kt} \ \ \ , \ \ \ a_k(0) = v^T_kx(0)$

x(t) = \sum_ka_k(0)e^{\lambda_k\beta t} \\x(t) \approx v_1e^{\lambda_1\beta t}

위 식을 해석해보면 $\lambda_1$ 은 가장 큰 eigenvalue값이고 이때의 eigenvector는 $v_1$ 이 된다.
각각의 노드가 t시간에 감염될 확률은 그 노드의 eigenvector값에 해당하고 이는 이전에 eigenvector centrality에서 배웠듯이 그 노드가 다른 노드들과 얼마나 밀접한 연관이 있는지 알려주는 지표이다. 즉 여러 노드와 연결되어있을수록 감염될 확률이 높아진다.
또한 $\lambda_1$ 즉 eigenvector값에 따라 증가속도도 변하게 된다.

Simulation

위 수식처럼 사용하는 것 이외에 간단하게 시뮬레이션으로 값을 얻어내는 방식이 있을 수 있다
각각의 노드가 S,I의 상태를 가지게하고 각각의 t마다 $\beta$ 확률로 이웃의 노드를 감염시키는 것을 반복하는 것이다.
우리가 실제 이론적으로 본 것과 유사한 값을 얻을 수 있다.

SIS model

Mathematical

\frac{dx_i(t)}{dt} = \beta s_i(t)\sum_jA_{ij}x_j(t) - \gamma x_i

SI model과 비슷한데 여기서는 회복률을 담당하는 항을 하나 추가하였다.
위 과정을 모두 생략하고 결과만 얻어보자면

x(t) = \sum_kak(0)v_ke^{(\beta \lambda_k - \gamma)t}

이 때 $\beta \lambda_k > \gamma$ 라면 $x(t) \rarr v_1e^{(\beta \lambda_1 - \gamma)t}$ 로 수렴하게될 것이고
$\beta \lambda_1 < \gamma$ 라면 $x(t) \rarr 0$ 으로 수렴하게될 것이다.
$\frac{1}{\lambda_1}$ 을 임계값 $R$ 로 두면
- $\frac{\beta}{\gamma} > R$ 일 때 질병의 확산이 빠를 것이고
- $\frac{\beta}{\gamma} < R$ 이면 질병이 시간에 거쳐 사라질 것이다.

Simulation

초기 감염 노드를 랜덤으로 정한다.
SI model과 동일한 방법으로 감염은 진행되지만 $\frac{1}{\gamma}$ 번 이후에 감염이 회복되어 다시 비감염상태로 돌아간다.

SIR model

Mathematical

\frac{dx_i(t)}{dt} = \beta s_i(t)\sum_jA_{ij}x_j(t) - \gamma x_i

\frac{dr_i}{dt} = \gamma x_i

앞에서와 유사하게 다음과 같이 시작할 수 있고 이 식을 풀게되면

x(t) \approx v_1e^{(\beta \lambda_1 - \gamma)t}

SIS 모델에서 임계치가 높을 때의 시나리오와 같은 결과를 얻을 수 있다.

Simulation

시뮬레이션도 SIS와 동일한 알고리즘이지만 감염 후 회복이 되고 S가 아닌 R이라는 그룹에 들어가 다시 감염되지 않는다라는 특징이 있다.

Infection in Diverse Networks

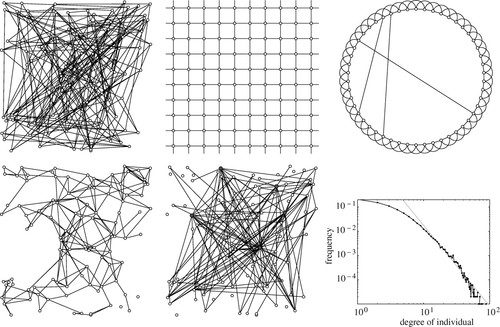
각각의 이 모델에서 전염병의 전파 속도가 어떻게 다른지 분석해보자
순서대로 random, lattice, small world, spatial, scale-free network를 표현한 그림이다

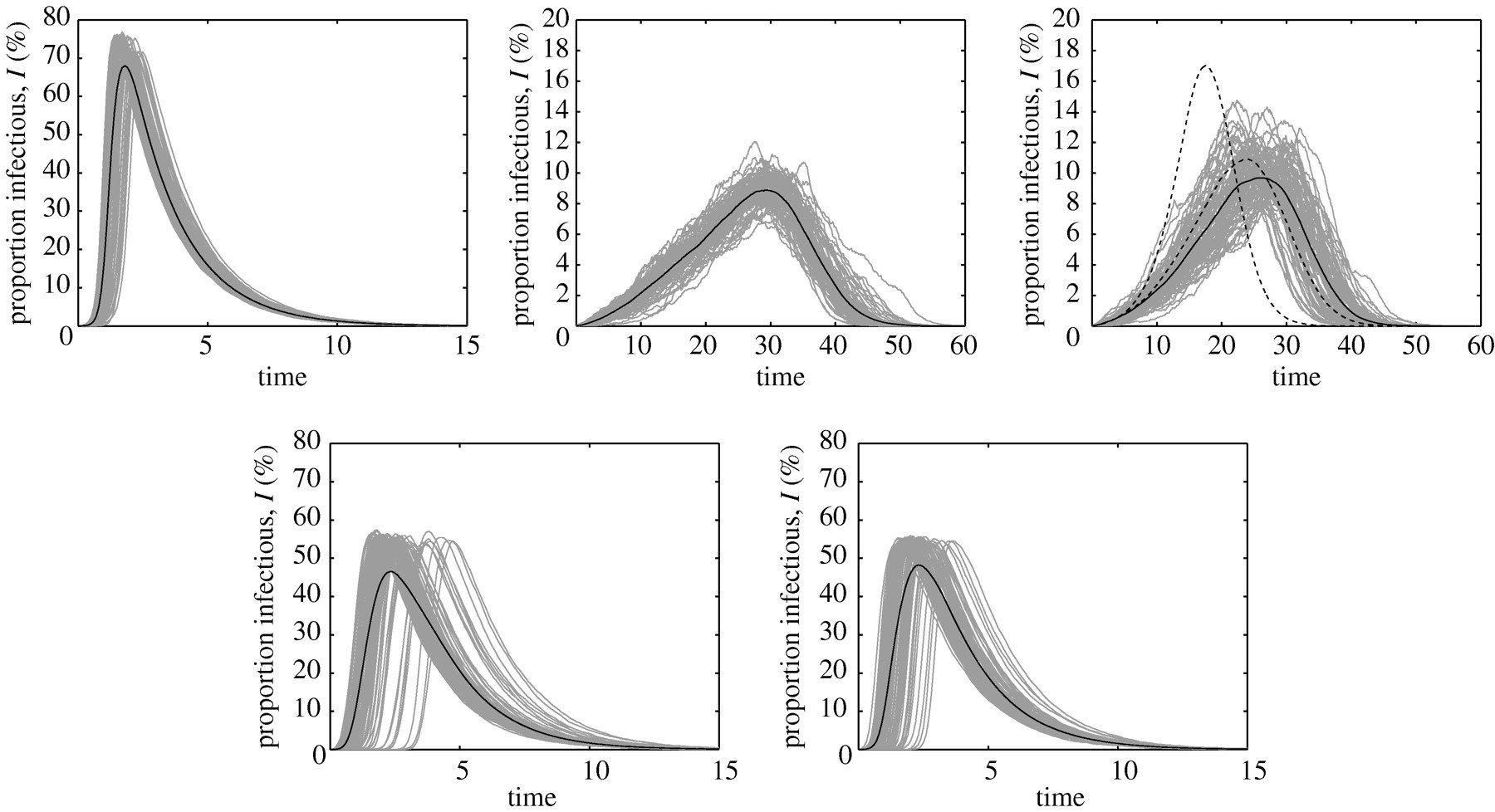
일반적으로 지름이 작으면 전파가 빠르고 지름이 크면 전파가 느리다고 기대할 수 있다.
실제로 대부분은 그 경향성을 따르지만 우리의 예상과는 조금 달리 맨 마지막 scale-free network가 random network보다 전파속도가 느리다는 것을 알 수 있다.
그 이유는 일반적으로 scale-free network에서 hub를 거치지 않는다면 전파속도가 그렇게 빠르지 않을 것이고 hub를 거치지않을 확률이 꽤 높다라고 생각해볼 수 있다.

이전 포스트

[Network Science]9. Epidemics on Networks 1

다음 포스트

[Network Science]11.Node Classification

0개의 댓글