[Network Science]11.Node Classification

YongUk·2025년 2월 14일
GNNGraphnetwork science

Graph Theory

목록 보기
13/17

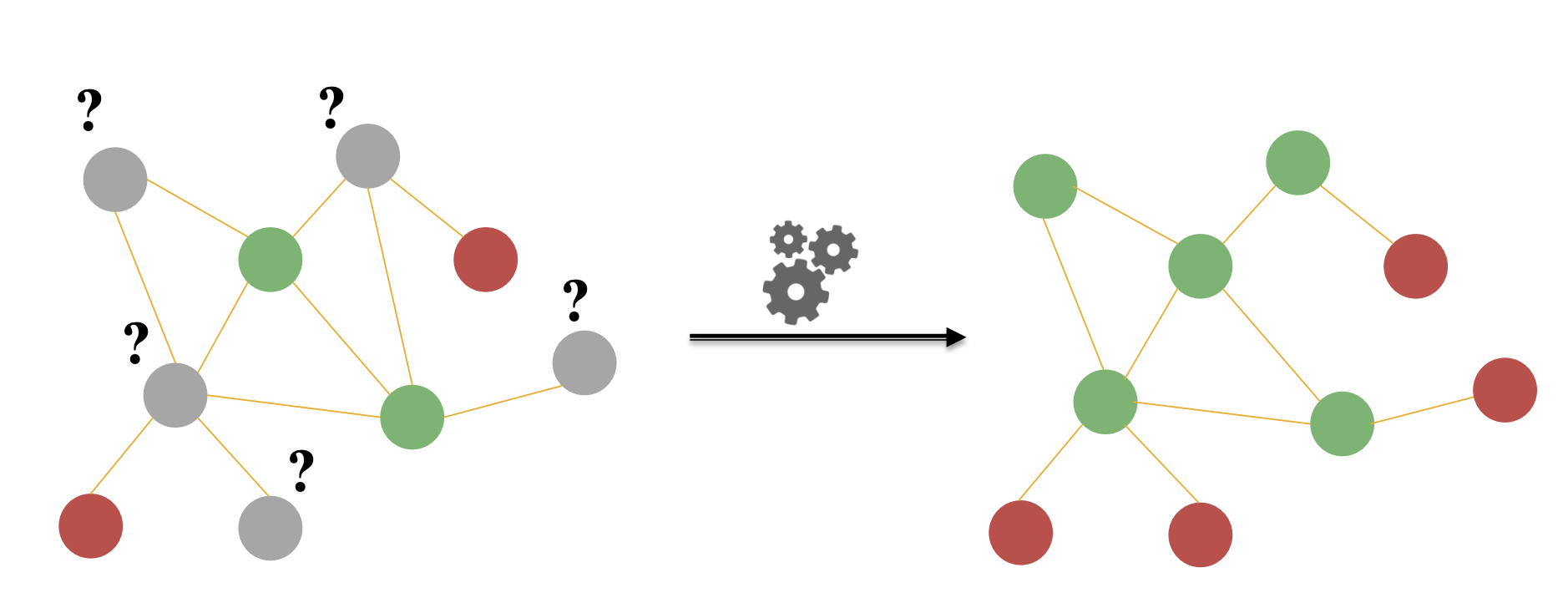
  • Node Classification이란 레이블이 없는 노드에 레이블을 부여할 수 있도록 하는 방식이다.
  • 혹은 레이블이 있는 노드로부터 없는 노드로 레이블을 확장시켜 부여하는 것으로도 볼 수 있다.
  • 이러한 예측에 논리적 기반이 되는 원리는 비슷한 특성을 가진 노드끼리 연결된다는 것이다. 이것을 반대로 사용하면 연결되어있으면 비슷한 특성을 가질 가능성이 높다라고 생각할 수 있고 기본적으로 연결되어있는 노드들의 특성을 기반으로 현재 라벨링되지 않은 노드의 특성를 분류할 수 있다.

Supervised Learning

  • 가장 기본적으로 내가 연결되어있는 이웃들의 클래스 정보를 이용하여 분류하는 것이다.
  • 즉 현재 노드의 이웃 중 A클래스의 노드가 더 많다면 현대 노드도 A클래스로 분류된다라는 것이다.
  • 만약 위 그림의 아래쪽 레이블이 없는 노드처럼 이웃에게도 레이블이 없다면 반복적인 계산을 하여 특정 확률에 수렴시켜 구할 수 있다.

Semi-supervised Learning

Random Walk Method

absorbing states

  • 기본적으로 우리가 아는 것은 random walk를 하는 도중 더이상 이동할 수 없는 상태를 말한다.
  • 이 random walk method에서는 레이블이 없는 노드에서 시작하여 레이블이 있는 노드에 도착하면 더 이상 다른 노드로 움직이지 못하도록 할 것이다.
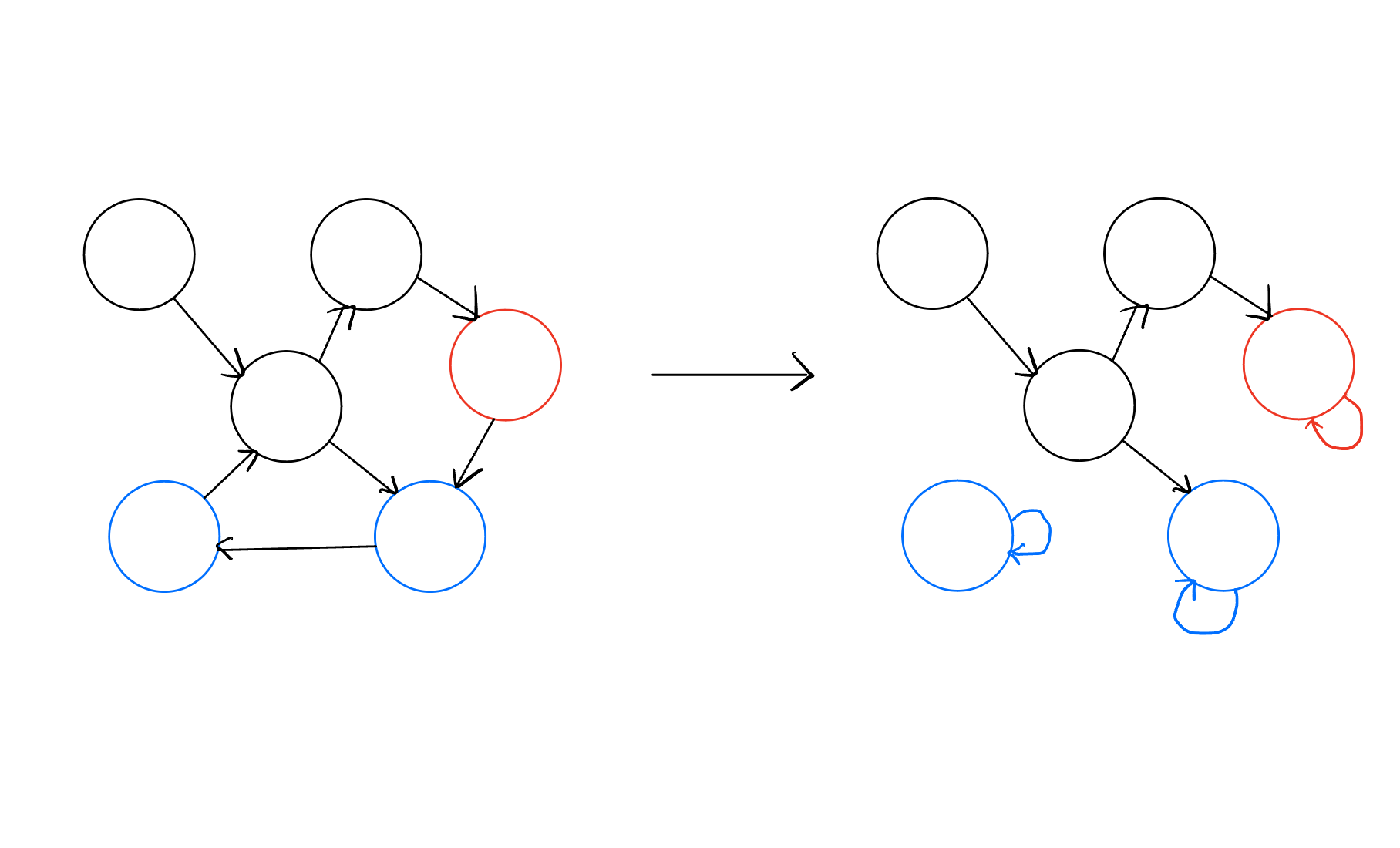
  • 이것을 실현하기 위해 레이블 된 노드를 대상으로 다음과 같이 특정 노드에서 나가는 out-going edge를 모두 제거한 후 self-loop 하나만 추가한다.

Mathematical

yi^[c]=∑j∈Vlpij∞yj[c]\hat{y_i}\left[c\right] = \sum_{j \in V_l} p_{ij} ^\infin y_j \left[c\right]
  • 출력으로 나오는 yi[c]y_i [c]는 라벨링되지 않는 노드 i가 클래스 c일 확률이다
  • 입력에 필요한 pijp_{ij}는 위 absorbing state를 구하는 과정이 무한히 반복하였을 때 i에서 j노드로 갈 확률이 수렴하는 확률 값이 될 것이고 이 때 yj[c]y_j[c]는 c로 레이블 된 노드는 1이될 것이고 아니면 0인 binary형식의 vector이다.

Random Walk Matrix

  • Random walk matrix는 우리가 이전에 이미 많이 보았다.
P=D−1AP = D^{-1}A
  • 여기서는 teleportation이 필요없기 때문에 다음과 같이 간단하게 나타낼 수 있다.
  • 이 때 우리는 편의를 위해 이 P에서의 노드들의 순서를 조금 수정하여 나타낼 수 있다.
P=(PllPluPulPuu)=(I0PulPuu)P = \begin{pmatrix} P_{ll} & P_{lu} \\ P_{ul} & P_{uu}\end{pmatrix} = \begin{pmatrix}I & 0 \\ P_{ul} & P_{uu}\end{pmatrix}
  • label이 있는 것과 없는 것을 다음과 같이 묶어서 두면 block matrix의 형태로 나타낼 수 있다
  • PllP_{ll}은 label이 있는 노드에서 label이 있는 노드로 가는 길인데 이는 self-loop밖에 없기 때문에 다음과 같이 identity matrix형태가 될 것이다.
  • PluP_{lu}는 label이 있는 노드에서 label이 없는 노드로 가는 것인데 이러한 것은 없기 때문에 zero matrix로 나타낸다.
  • PP를 다음과 같이 수정한 후 이 PP를 ∞\infin로 보냈을 때 최종적으로 다음과 같이 나오게된다.
P∞=(I0(I−Puu)−1Pul0)P^\infin = \begin{pmatrix} I & 0 \\ (I-P_{uu})^{-1}P_{ul} & 0\end{pmatrix}
  • 이것을 이용하여 최종적으로 답을 구해보면
(Yl^Yu^)=(I0(I−Puu)−1Pul0)(YlYu)\begin{pmatrix} \hat{Y_l} \\ \hat{Y_u}\end{pmatrix}= \begin{pmatrix} I & 0 \\ (I-P_{uu})^{-1}P_{ul} & 0\end{pmatrix} \begin{pmatrix} Y_l \\ Y_u\end{pmatrix}
Yu^=(I−Puu)−1PulYl\hat{Y_u} = (I-P_{uu})^{-1}P_{ul}Y_l

Simulation

  1. 라벨링되지 않는 노드 i에서 탐색을 시작한다.
  2. 라벨링된 노드를 하나 만나게 되면 탐색을 중지한다.(absorbing state)
  3. 이 과정을 반복하여 값을 수렴시킨 후 노드 i가 가장 만날 확률이 높은 클래스를 선택하게된다.
  • 위와 같이 공식을 이용하여 풀어도 되고 시뮬레이션을 돌려서 해결할 수도 있을 것이다.
  • 하지만 공식의 시간복잡도가 높지 않으므로 개인적으로 시뮬레이션보다는 공식을 이용하는게 훨씬 빠르고 정확할 것이라 생각한다.

Regression on graphs

  • 사실 graph에서의 regression이라는 것이 굉장히 생소하고 추상적인 것 같은 개념이다.
  • 먼저 일반적인 머신러닝 기법처럼 우리는 node을 잘 설명하는 선형회귀식을 구해야한다.
∑i∈Vl(yi^−yi)2=∥Yl^−Yl∥2\sum_{i \in V_l}(\hat{y_i}-y_i)^2 = \|\hat{Y_l}-Y_l\|^2
  • 위 식을 최소화하는 선형회귀식을 구해야한다.
  • 이 때 선형회귀식이 너무 복잡하게 과적합되는 것을 방지하기 위해 그래프에서는 규제항을 추가할 수 있다.
  • 일반적인 머신러닝처럼 전체적인 값을 작게 만드는 규제항을 추가할 수 있다.
ϵ∑i∈Vyi^2=ϵ∥Y^∥2\epsilon\sum_{i \in V} \hat{y_i}^2 = \epsilon\| \hat{Y}\|^2
  • 추가적으로 그래프에서만 적용가능한 조금 특이한 규제항도 있다. 기본적인 아이디어는 서로 이웃이 노드끼리의 선형회귀 결과는 비슷해야한다라는 것이다.
12∑i,j∈VAij(yi^−yj^)2=Y^T(D−A)Y^=YT^LY^\frac{1}{2}\sum_{i,j \in V} A_{ij}(\hat{y_i}-\hat{y_j})^2 = \hat{Y}^T(D-A)\hat{Y} = \hat{Y^T}L\hat{Y}

Laplacian Regularization

  • 위 정보들을 조합하여 식을 만들게 되면
Q(Y^)=12∑i,j∈VAij(yi^−yj^)2+μ∑i∈Vl(yi^−yi)2Q(Y^)=YT^LY^+μ∥Yl^−Yl∥2Q(\hat{Y}) = \frac{1}{2}\sum_{i,j \in V} A_{ij}(\hat{y_i}-\hat{y_j})^2 + \mu\sum_{i \in V_l}(\hat{y_i}-y_i)^2 \\ Q(\hat{Y})= \hat{Y^T}L\hat{Y} + \mu\|\hat{Y_l}-Y_l\|^2
  • 다음과 같이 나타낼 수 있다.
Lej=λjejLe_j = \lambda_je_j
  • 위 eigenvalue 식을 풀어서 p개의 작은 고유값을 가지는 eigenvector를 선택한다. (p는 하이퍼파라미터로써 조정가능함
Err(a)=∑i∈Vl(yi−∑j=1pajeji)2Err(a) = \sum_{i \in V_l}\left (y_i-\sum_{j=1}^p a_je_{ji}\right )^2
  • 이렇게 eigenvector들을 이용하여 선형회귀식을 구하고 이 식을 최적화할 수 있는 aja_j를 찾는 것이 Laplacian Regularization의 핵심이다.
profile
YongUk
이전 포스트

[Network Science]10. Epidemics on Networks 2

다음 포스트

[Network Science]12.Link Prediction

0개의 댓글