[Network Science]9. Epidemics on Networks 1

YongUk·2025년 2월 11일
GNNGraphnetwork science

Graph Theory

목록 보기
11/17
  • 말 그대로 네트워크에서 전염이 어떻게 이루어지는지에 대한 내용을 다룬다. 노드에서 다른 노드로 전염되는 특히 전염병과 관련하여 어떤 로직으로 이 현상을 설명할 수 있는지에 대한 기초 인사이트들에 대해 볼 것이다.

Simple Model

  • 다음은 가장 기본적인 아이디어이다

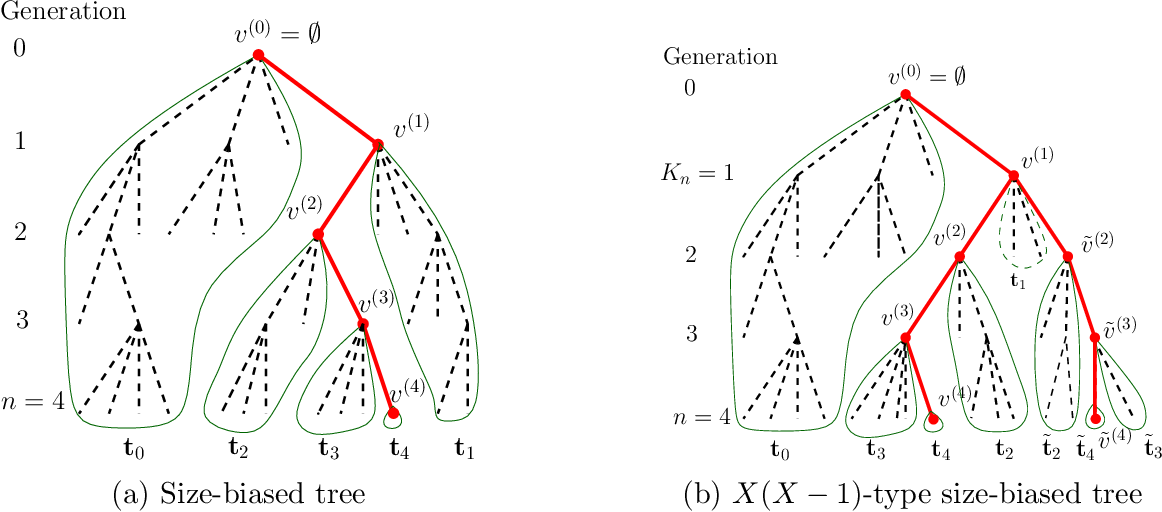
    1. 사람들을 트리의 형태로 나타낸다
    2. 초기에 감염자가 존재한다
    3. 모든 감염자는 평균적으로 ⟨k⟩\langle k \rangle의 사람을 만나고 각각의 감염확률은 pp이다.
    4. R0=p⟨k⟩R_0 = p\langle k \rangle : 맨 처음 감염되는 사람들의 수이다.
    5. 그 다음 스텝부터는 R0n=(p⟨k⟩)nR_0^n = (p\langle k \rangle)^n 명의 사람들이 감염될 것이다.

  • 이때 p⟨k⟩>1p\langle k \rangle > 1 이라면 감염자는 기하급수적으로 점점 늘어날 것이고 p(k)<1p(k) < 1 이라면 감염자는 점점 줄어들어 0으로 수렴할 것이다.

  • 이때 R0R_0을 basic reproduction number라고 하고 1명이 평균적으로 감염시키는 사람의 숫자이다.

Mathematical Epidemiology

  • Kermack과 Mckendrick에 의해 연구되었으며 수학적으로 이 현상을 표현하기 위한 모델들을 제안하였다.
  • 가장 기본이되는 몇가지 파라미터가 존재한다
    • S(t) : 아직 감염되지 않은 사람
    • I(t) : 이미 감염되어 전파가능성이 있는 사람
    • R(t) : 회복되어 병에 걸리지 않고 전파가능성도 없는 사람

SI model

Mathematical

S(t)+I(t)=NS(t) + I(t) = N
  • 비감염자와 감염자로 이루어져있는 모델이다
I(t+δt)=I(t)+βS(t)NI(t)δtI(t + \delta t) = I(t) + \beta\frac{S(t)}{N}I(t)\delta t
  • 여기서 β\beta는 확산 속도를 조절해주는 파라미터이다.
  • 즉 감염가능한 사람 중 일정 비율만큼 시간에 따라 감염이 된다.
  • 이를 시간에 따른 감염자 수의 변화량을 나타내어볼 수 있다.
dI(t)dt=βS(t)NI(t)\frac{dI(t)}{dt} = \beta\frac{S(t)}{N}I(t)
  • 좀 더 간단하게 표현하기 위해 다음과 같은 비율의 개념을 사용한다면
    i(t)=I(t)N   ,   s(t)=S(t)Ni(t) = \frac{I(t)}{N} \ \ \ , \ \ \ s(t) = \frac{S(t)}{N}
    di(t)dt=βs(t)i(t)   ,   ds(t)dt=−βs(t)i(t)   ,   s(t)+i(t)=1\frac{di(t)}{dt} = \beta s(t)i(t) \ \ \ , \ \ \ \frac{ds(t)}{dt} = -\beta s(t)i(t) \ \ \ , \ \ \ s(t) + i(t) = 1
  • 위와같이 수정할 수 있다. 전체적으로 정리하면 다음과 같은 미분방정식을 얻을 수 있고
    di(t)dt=β(1−i(t))i(t)\frac{di(t)}{dt} = \beta(1-i(t))i(t)

Conclusion

i(t)=i0i0+(1−i0)e−βti(t) = \frac{i_0}{i_0+(1-i_0)e^{-\beta t}}
  • 위 모양으로 정리되게 된다.
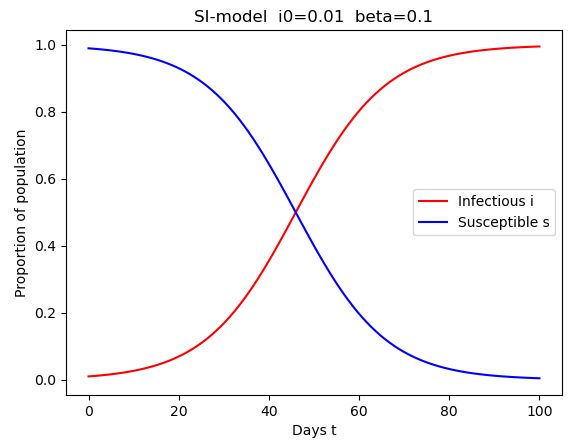
  • 위 식에서 얻을 수 있는 것은 간단하게 t=0t=0일 때는 초기 감염가 i0i_0가 존재하고 t→∞t \rarr \infin일때 감염자수는 1 로 수렴한다는 것을 알 수 있다.
  • 즉 회복이 없는 모델에서의 시나리오는 결국 모두 감염되는 엔딩으로 끝난다.

SIS model

Mathematical

  • 이 모델의 가장 큰 특징은 회복이 가능하다는 것이다. 말 그대로 S→I→S 의 과정이 가능하다는 것이고 재감염 또한 가능하다는 것을 의미한다.
di(t)dt=βs(t)i(t)−γi(t)   ,   ds(t)dt=−βs(t)i(t)+γi(t)\frac{di(t)}{dt} = \beta s(t)i(t) - \gamma i(t) \ \ \ , \ \ \ \frac{ds(t)}{dt} = -\beta s(t)i(t) + \gamma i(t)
s(t)+i(t)=1s(t) + i(t) = 1
  • 이 때 γ\gamma는 회복률이고 감염자에서 회복되어 비감염자로 바뀌는 정도를 말한다
di(t)dt=(β−γ−βi(t))i(t)\frac{di(t)}{dt} = (\beta - \gamma - \beta i(t))i(t)
  • 위와 같이 수정하여 감여자 수 변화량을 나타낼 수 있다.
i(t)=(1−γβ)CC+e−(β−γ)t   ,   C=βi0β−γ−βi0i(t) = \left ( 1 - \frac{\gamma}{\beta} \right)\frac{C}{C+e^{-(\beta-\gamma)t}} \ \ \ , \ \ \ C = \frac{\beta i_0}{\beta-\gamma-\beta i_0}
  • 미분방정식을 풀면 다음과 같은 공식이 도출된다

Conclusion

  • 위 식은 두가지 관점에서 생각해보아야한다. t→∞t \rarr \infin이라면
    • β>γ\beta > \gamma 일 때 i(t)→(1−γβ)i(t) \rarr \left ( 1-\frac{\gamma}{\beta} \right)
    • β<γ\beta < \gamma 일 때 i(t)→0i(t) \rarr 0
    • 감염률이 더 높다면 일정 구간에 수렴할 것이고 회복률이 더 높다면 0으로 수렴할 것이다.

SIR model

Mathematical

  • SIS 모델과 구조적으로 동일하지만 I→R 부분만 다르다. SIS 모델에서는 회복된 사람이 다시 재감염이 가능하였지만 I→R은 완전 면역을 얻어 재감염이 되지 않는 모델이다.
  • 따라서 이 모델에서는 S,I,R 이라는 3가지 상태가 존재한다.
di(t)dt=βs(t)i(t)−γi(t)   ,   ds(t)dt=−βs(t)i(t)   ,   dr(t)dt=γi(t)\frac{di(t)}{dt} = \beta s(t)i(t) - \gamma i(t) \ \ \ , \ \ \ \frac{ds(t)}{dt} = -\beta s(t)i(t) \ \ \ , \ \ \ \frac{dr(t)}{dt} = \gamma i(t)
s+i+r=1s+i+r = 1
  • 위가 가장 기본적인 SIR모델의 아이디어이다. 하지만 종속성이 너무 크기 때문에 이를 깔끔하게 정리하기란 매우 어렵다.
drdt=γ(1−r−s0e−βγr)\frac{dr}{dt} = \gamma(1 - r - s_0e^{-\frac{\beta}{\gamma}r})
  • 회복한 사람의 수를 다음과 같이 나타낼 수 있고 t→∞t\rarr \infin 일 때 drdt=0  ,   r∞=const\frac{dr}{dt} =0 \ \ , \ \ \ r_{\infin}=const 를 이용하여 이 식을 정리할 수 있다.
1−r∞=s0e−βγr∞   ,   s0≈11 - r_{\infin} = s_0e^{-\frac{\beta}{\gamma}r_{\infin}} \ \ \ , \ \ \ s_0 \approx 1
r∞=1−e−βγr∞r_{\infin} = 1 -e^{-\frac{\beta}{\gamma}r_{\infin}}
  • 위와같이 대략적으로 정리할 수 있다. 위 식은 이전에 random graph의 threshold를 구할 때 보았던 공식과 동일하다 (s=1−e−λs)(s = 1 - e^{-\lambda s}). 이것을 그래프를 그림을 통해 다시 한번 계산해본다면 다음과 같다. (자세한 증명은 3.Random Graph에서 다루었다.)

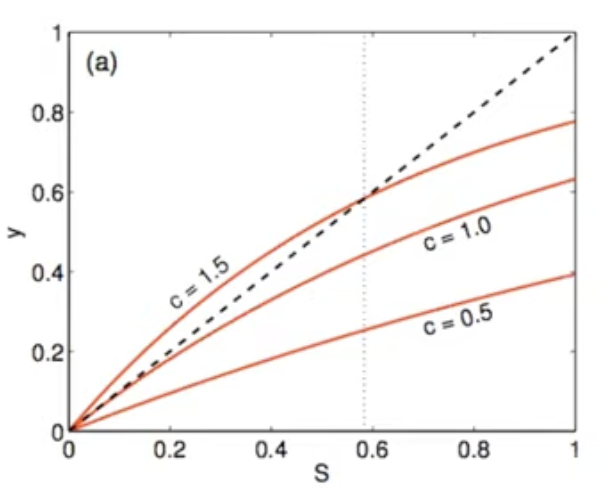
  • 위 식에서 교점 즉 r∞r_{\infin}가 0 이외의 값이 존재하기 위해서는 1보다 커야한다. 이 때 이 c=βγc = \frac{\beta}{\gamma}이고 즉 회복률보다 감염률이 더 높아야한다는 것을 의미한다. 이것을 basic reproduction number로 보았을 때 임계값이 1이 된다.

Conclusion

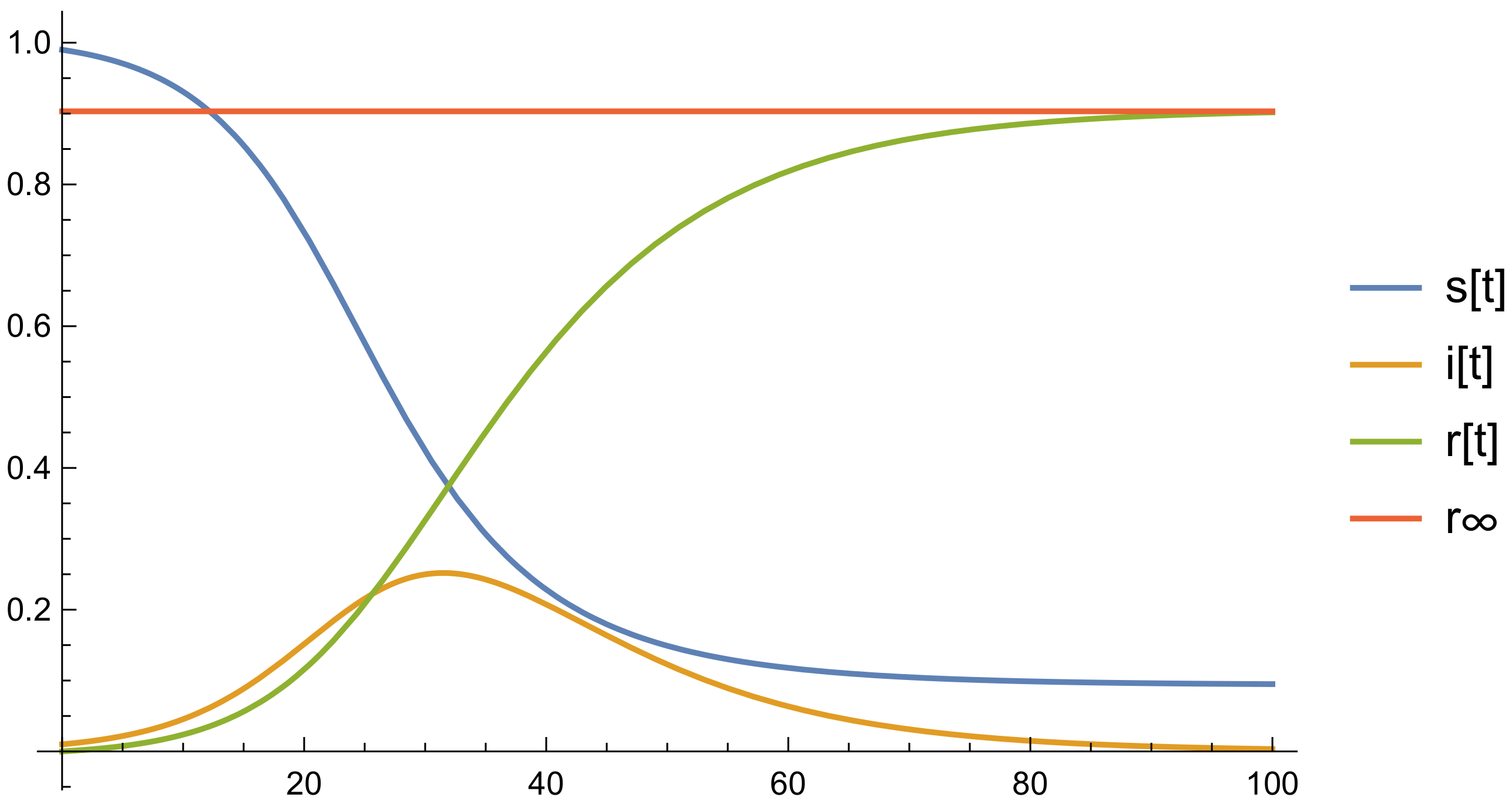
  • 위 그래프는 감염률이 회복률보다 클 때의 그래프이다 (β>γ)( \beta > \gamma)
  • 우리는 위 그래프를 분석하게되면 감염자 i에서 최고점이 언제 얼마나 발생하는지를 예측할 수 있다. 이를 통해 실제 환경에서 환자를 수용하는 환경을 미리 대비할 수 있다.
  • 이 때 β\beta의 경우는 우리가 마스크를 쓰거나 손을 잘 씻거나 등등의 방식으로 줄일 수 있고 그렇다면 정점은 점점 낮은 곳에 형성되며 이 값이 γ\gamma보다 작아지게되면 정점은 사라지게될 것이다.

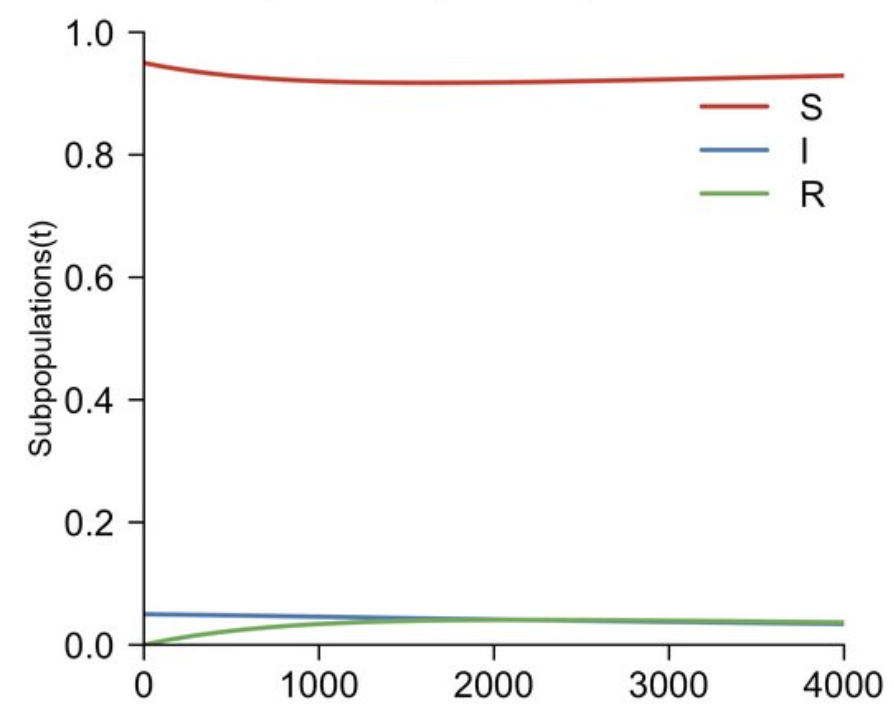
  • 감염률보다 회복률이 더 크다면 다음과 같이 정점이 존재하지 않고 감염률은 점점 낮아지게 된다.
  • 감염률은 임계값과 상관없이 0으로 수렴하게된다.

More model

  • 위를 기반으로 하는 더 구체적인 모델들이 존재한다. 이 특히 S,I,R 이외의 여러가지 상태를 다룬다라는 점에서 매우 특이하고 상태가 늘어날 때마다 파라미터가 늘어나기에 모델이 더 복잡해진다.

SIRS

  • SIR모델에서 일정시간이 지나면 면역이 사라지며 일정비율에 따라 R→S로 가는 모델이다

SEIRS

  • E는 감염은 되었지만 전염성은 없는 사람의 수이고 나머지는 모두 동일하다.
  • 즉, 비감염 → 감염(비전염) → 감염(전염) → 회복 → 비감염 으로 진행된다고 볼 수 있다.

SEIR-v

  • volnerable 즉 해당 질병에 취약한 계층과 덜 취약한 계층 간에 계수를 달리 하여 분석하는 모델이다. 이 모델에서는 실제로 Death에 해당하는 영역도 존재하고 일반적으로 취약계층이 Death로 가는 비율이 더 많다.

SEIIHURD

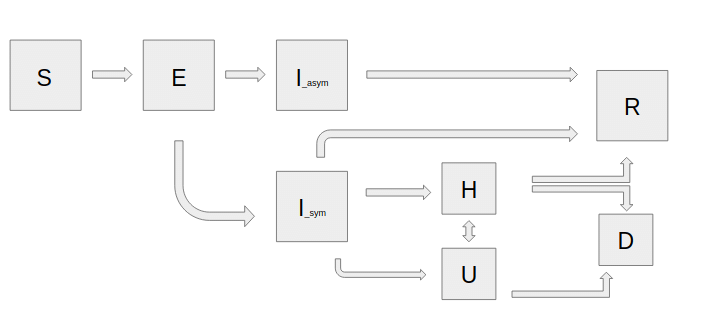
  • I가 각각 증상자와 무증상자로 나뉘는데 무증상자는 시간이 지남에 따라 쉽게 회복된다.
  • 만약 증상자일 경우는 일반 병원을 가거나 중환자실로 간다.
  • 중환자실에서는 죽거나 일반 병동으로 연결되고 일반 병동에서는 죽거나 중환자실로 가거나 회복되는 프로세스를 가지고 있다.
profile
YongUk
이전 포스트

[Network Science]8. Community Detection

다음 포스트

[Network Science]10. Epidemics on Networks 2

0개의 댓글