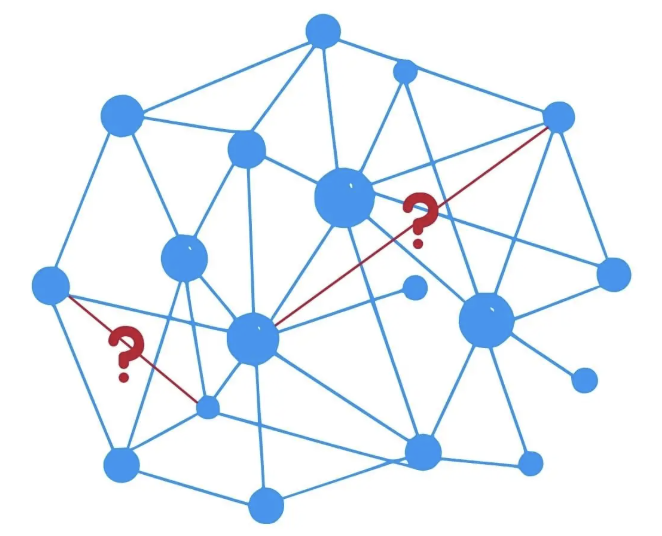
---

• 서로 다른 노드 사이의 edge가 있을지 없을지, 가중치가 얼마일지 혹은 어떤 종류의 edge가 있을지 등등을 예측하는 분야가 Link. prediction이다
• 하지만 이러한 예측을 정확하게하는 것에는 한계가 있는데 $|V|$개의 node가 있다고하였을 때 총 $\frac{|V|(|V|-1)}{2}$개의 edge가 존재할 수 있고 이러한 edge를 정확하게 예측하기 위해서는 모든 경우의 수를 대입해보면 $O(|V|^2)$의 시간이 걸리게 된다.
• 다시 말하면 무작위로 추측했을 때 완벽한 예측을 할 확률은 $\frac{1}{|V|^2}$이다.
• 따라서 이 문제의 최적의 해를 찾기위한 다양한 기법들이 존재한다.

Similarity based Algorithms

---

Algorithm

---

1. 각각의 노드 쌍에 대해 유사도 점수를 계산한다.
2. 계산한 유사도 점수에 따라 내림차순으로 정렬한다.
3. 상위 n개의 쌍을 선정하여 해당 쌍에 새로운 edge를 할당한다
4. $Precision = \frac{TP}{TP+FP}$ 를 이용하여 알고리즘의 성능을 평가한다.

• 하지만 모든 노드 쌍에 대해 유사도 점수를 계산하는 알고리즘은 $O(N^2)$이므로 굉장히 비효율적으로 보인다.

Local similarity

---

• 위 알고리즘에 1번에 해당하는 유사도를 측정하는 지표들이다.
• 지역적인 측면에서 이웃의 정보를 이용하여 계산하는 방식들이다.

• 단순히 공통 이웃의 수를 계산한다.

• 단순이 공통 이웃의 수만 측정하는 것은 각 노드의 특성에 따라 다른 값을 보이기 때문에 다음과 같이 약간의 정규화를 하는 Jaccard’s coefficient를 활용할 수 있다.

• 위와 같이 공통 이웃들에 가중평균을 적용하여 이웃이 적은 노드와 연결되었을 때 그 유사도가 더 크게 작용하고 이웃이 많은 노드와 연결되었을 때 그것이 크게 중요하지 않음을 표현할 수 있다.
• 이 식을 조금 응용하여 아래에 Admic-Adar 점수를 계산할 수 있는데 일반적으로 잘 작동한다.

Preferential attachment

• 다음과 같이 서로의 이웃 수를 이용하여 단순히 측정할 수 있다.
• 이를 뒷바침하는 이론은 preferential attachment이고 차수가 높은 노드는 차수가 높은 노드끼리의 연결될 확률이 높다라는 것이다.
• 하지만 이 방식을 사용하면 차수가 낮은 노드의 연결에 대해서는 과소평가하는 경향이 있기 때문에 좋은 방식인지에 대한 의문이 든다.

Clustering coefficient

• 위와 비슷한 논리로 클러스터링 계수가 높은 노드끼리의 연결될 확률이 높다라는 이론을 배경으로 한다.

Path based method

---

• 위 측정법들이 모두 노드의 지역적인 부분만 다루었다면 전역적으로 멀리 떨어져있는 노드와의 유사도도 측정할 수 있어야할 것이다.
• 그러한 것들을 path를 기반으로 측정한다

Shortest path

• 두 노드 사이에 경로가 존재할 때 그 중 최단 경로의 길이를 유사도로 사용한다.
• 가장 기본적인 방식이지만 small world에서 최단경로의 길이의 범위가 다양하지 않다는 측면에서 잘 작동하는지는 의문이다

Katz score

• 위 알고리즘과 달리 두 노드 사이에 존재하는 모든 경로에 대해 측정한다.
• 다만 경로의 길이(s)가 길수록 $\beta^s$를 이용하여 가중치를 줄이는 방식을 사용한다.
• matrix를 사용하여 오른쪽과 같이 간단한 공식을 통해 계산 가능하다.

Personalized RageRank

• 기존의 pagerank 알고리즘은 전체 네트워크에서 중요한 노드를 찾는 방식이다.
• Personalized PageRank는 이와 달리 특정 노드를 기준으로 하였을 때 중요한 노드를 찾는 변형 알고리즘이다.
• 차이점은 PPR의 경우 초기 확률은 모든 노드에 동일하게 두지 않고 시작 노드에 초점을 맞추어 분포시킨다.

Random walk

• random walk를 하여 노드 i에서 노드 j에 도달하는 평균 step을 이용하여 측정한다.

• 양쪽에서의 step을 모두 이용하여 측정할 수도 있다.

SimRank

• 이전에 한 번 보았던 유사성 지표로 재귀적으로 계산하는 Simrank라는 지표도 있다.

Community based method

---

• $v_i, v_j$의 공통 이웃이 같은 클러스터 C에 들어간다면 위 점수는 높아지게 될 것이다.
• 즉 공통 이웃들도 같은 클러스터에 있다면 유사하다고 판단하는 것이다.

• 또한 추가적으로 위와 같은 식으로도 유사성을 측정할 수 있다.

Low-rank approximations

---

• 우리의 지금의 목표는 link prediction이며 이때에 사용할 것은 유사성 말고 또 다른 접근법도 있다.

• truncated SVD를 이용하여 잠재요소를 찾아내는 것이다. 이를 통해 $m\times n$ 의 행렬을 각각
  $m\times r , r \times r , r \times n$으로 나누어 해결할 수 있다. 이때 잠재요소인 $r \times r$을 이용하여 구할 수 있다.

Classification for Link prediction

---

• 이때까지 살펴본 알고리즘들은 일반적으로 소셜네트워크에서는 잘 작동한다. 하지만 이들이 다른 네트워크에서는 잘 작동하지 않을 수 있다. 따라서 이러한 작동을 조금 일반화할 수 있도록 link의 존재 여부에 따라 binary classification으로 이 문제를 해결하고자 한다.

imbalanced class distribution

• 하지만 graph에서 edge classification을 할 때 가장 큰 문제는 클래스 불균형 문제이다. 일반적으로 그래프 내에는 실제 연결된 edge보다 연결되지 않은 edge가 더 많을 것이기 때문이다.
• 하지만 이러면 불균형은 classification에서 굉장히 취약한 부분이다.
• 따라서 가중치를 부여하던지 혹은 다른 방법들을 이용하여 이 문제를 가장 먼저 해결해주어야한다

Supervised Learning

• 기존의 graph가 있을 때 현존하는 edge를 몇개 모르는 상태로 두고 존재하지 않는 edge도 몇개 모르는 상태로 둔다. 즉 이를 test set으로 활용한 후 나머지 edge데이터들에 대해 학습을 시킨 후 검증을 거친다.
• 이를 이용하여 이후에 ROC-curve를 만들어 서로 다른 알고리즘 간의 성능 비교도 할 수 있다.

Evolving networks

• 또 중요한 것은 진화하는 네트워크의 특성을 담아야한다는 것이다.
• 예를 들어 $t_0$부터 $t_k$까지의 시간 동안의 그래프를 보고 훈련시켜 $t_{k+1}$의 그래프로 평가를 하였다면 $t_1$부터 $t_{k+1}$의 그래프를 보고 $t_{k+2}$의 그래프를 예측하도록 구조를 만들어야한다.
• 이를 반복적으로 진행하면 보다 정교한 그래프가 형성될 것이다.