---

• 그래프에서의 노드들을 임베딩 공간으로 위치를 옮기는 것을 embedding이라고 한다.
• 다른말로는 encoding, projection이라고도 말을 한다.

Classic Techniques

SVD Projection

---

• Adjacency matrix를 SVD를 이용하여 분해한 값을 통해 임베딩 공간에 투영시킬 수 있다.

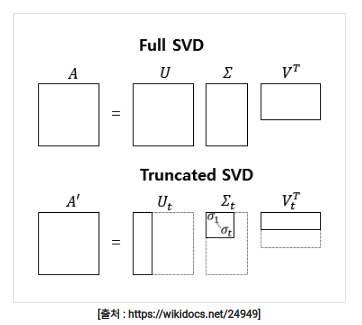
• 기본적으로 SVD를 분해하게되면 위와 같은 형태로 분해가 된다. $m\times n$의 matrix에서 $m\times m , m\times n , n \times n$ 총 3개의 행렬로 나뉘게 된다.
• 이때 truncated SVD라는 기법을 사용하여 뒤쪽에 있는 세부적인 내용은 지우고 앞쪽에 있는 중요한 부분만을 이용하여 분해할 수도 있다. 또한 차원 축소의 장점도 얻을 수 있다.
• 이 때 상위 $k$개의 중요한 값만 사용한다라고 했을 때 $m\times k , k\times k , k \times n$ 총 3개로 나뉠 수 있다.
• 이때 우리는 행렬 $U(m \times k)$에서 k를 임베딩 공간의 축의 개수라고 생각하였을 때 예를 들어 k가 2이면 이 matrix를 2차원 공간에 할당 시킬 수 있고 이것을 통해 즉각적인 임베딩을 시킬 수 있다.

Laplacian Embedding

---

• laplacian기법은 이전에 clustering에서 이미 한번 수식적으로 알아본 내용이다.
• 간단하게 laplacian matrix를 만들어서 이것의 eigenvalue와 eigenvector를 구한다.
• 이때 낮은 eigenvalue일수록 그래프를 더 많이 설명하고 가장 작은 2번 째 값부터 이것이 유효하다

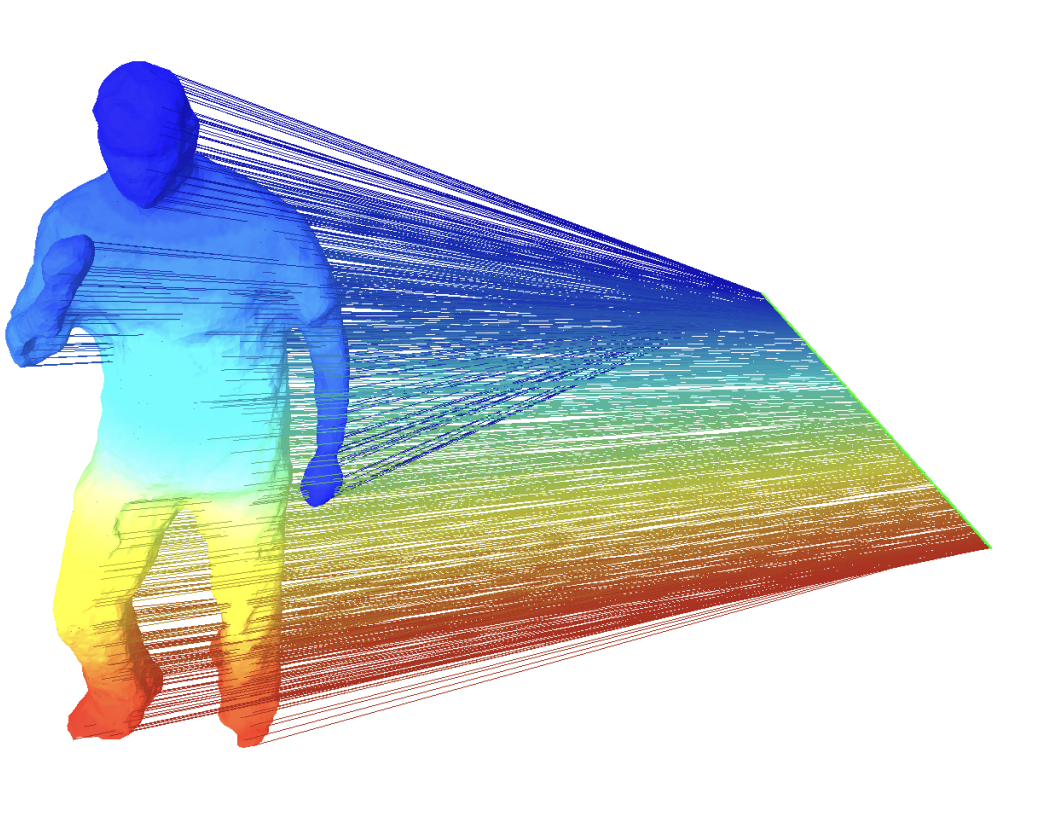
• 위와 같은 원본이 있다라고 생각해보았을 때 실제로 낮은 eigenvalue가 더 많이 설명하고 아래로 갈수록 조금 세부적인 부분들을 신경쓰는 것을 알 수 있다. 이를 통해 eigenvalue가 가장 낮은 하위 몇 개의 eigenvector 값을 임베딩 시킨다면 이것이 그래프를 대체로 설명하는 값이 될 것이라는 내용이다.

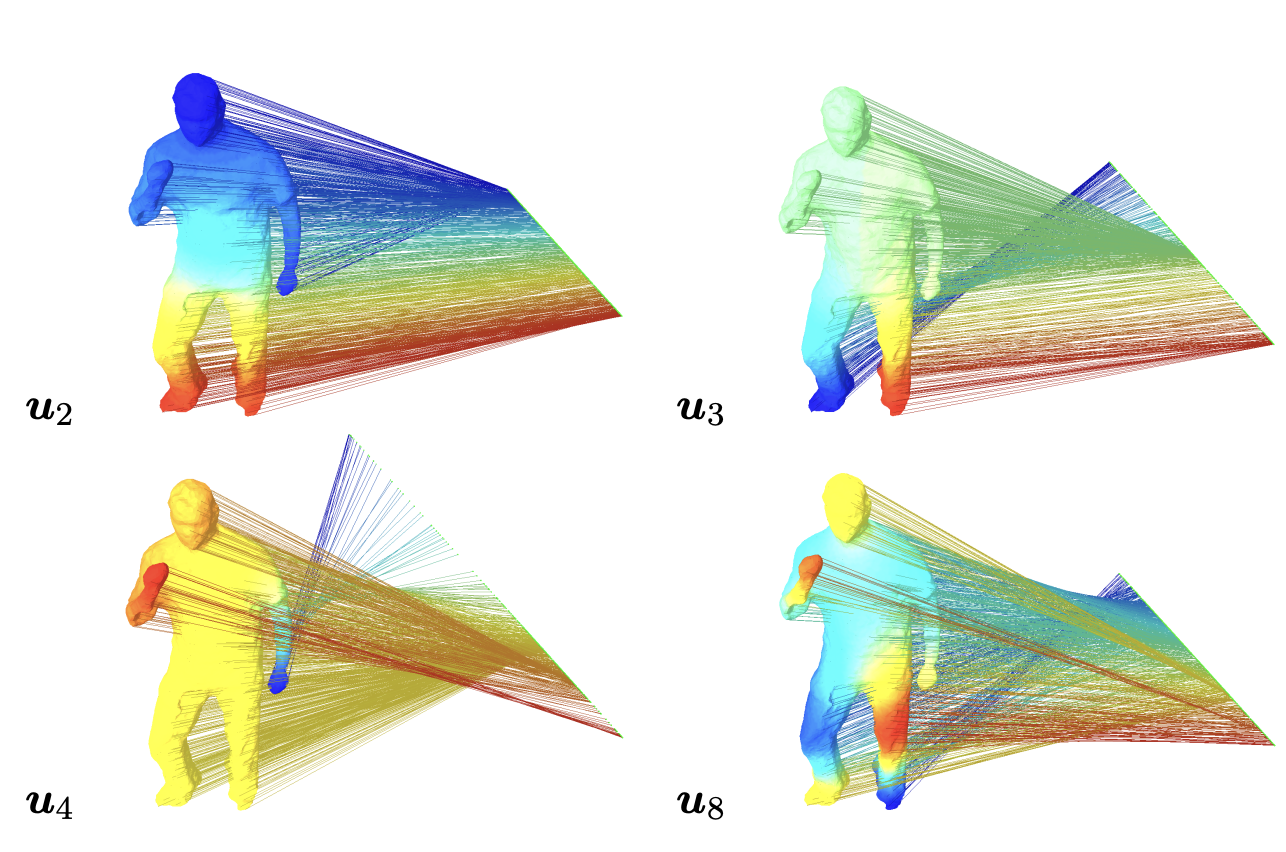
• laplacian matrix의 특성상 전체적인 데이터 구조를 반영하기 보다는 인접한 노드끼리의 연결을 상대적으로 많이 반영하는 기법이다

Modern Embedding Concept

---

• embedding을 할 때 다양한 요소들을 고려해볼 수 있다.
  1. 그래프에서 이웃이 노드끼리는 임베딩 공간에서도 가까이 있어야한다
  2. 그래프에서 community를 형성하는 노드들은 임베딩 공간에서도 community를 형성할 수 있어야한다.
  3. 그래프에서 중심성이나 구조적인 특정을 가지는 노드들은 임베딩 공간에서도 그 특징을 유지해야한다.
• 이러한 것을 만족시키기 위해서 그래프와 임베딩 공간에서 동일한 지표를 사용하여 유사도가 높았던 것은 계속높고 낮았던 것은 계속 낮게와 같이 유지되도록 최적화를 해줄 수 있다.
• 임베딩공간에서 유사도를 측정하는 것은 일반적으로 점곱을 이용한다. $similarity(u,v) = z_v^Tz_u$

Random Walk Embedding

---

기본 원리

• 특정 노드에서 K번의 random walk를 시행, 이것을 N번 반복한다.
• 각 시행마다 지나간 노드 시퀀스를 얻을 수 있을텐데 이때 각 시퀀스에는 K개의 데이터가 있을 것이고 이것이 총 N개의 시퀀스가 있는 것이다.
• 이때 서로 다른 두 노드가 N개의 시퀀스 중에 함께 나오는 것이 여러번 있다라는 것은 두 노드가 서로 유사하다는 의미로 임베딩 공간에서 내적 결과가 높게 나오도록 위치시킨다.

• 위와 같이 u가 나왔을 때 v가 나올 확률이 높으면 두 노드는 비슷하다고 판단할 수 있다.

Log-likelihood objective

• 목적함수는 다음과 같다

• 원래는 확률곱으로 계산하지만 편의를 위해 log likelihood를 사용한다
• 위 식을 간단하게 표현하면 $z_u$가 임베딩 공간에 있을 때 $N_R(u)$ 즉 랜덤워크로 생성된 u의 이웃들이 나올 확률 혹은 그것들과의 유사도를 최대화 시킨다는 것이다.
• 즉 임베딩 공간에서 랜덤워크로 생성된 시퀀스에 서로 많이 겹쳐 있는 노드들과 최대한 가까이 있어야한다.

Loss function

• 손실함수로 나타내면 다음과 같이 나타낼 수 있다.
• 여기서 의문은 $P(v|z_u)$를 어떻게 표현하는지이다.

• 위와 같이 두 노드의 내적값을 정규화하여 표현할 수 있다.

Negative Sampling

• 그럼 최종적으로 위와같이 나오게 되는데 이때 시간복잡도가 $O(|V|^2)$이 되기에 너무 복잡하다. 따라서 이를 보완하기 위해 negative sampling을 사용할 수 있다.
• negative sampling이란 소프트맥스 함수는 모든 클래스에 대해 확률을 개선해야하는 시간적 문제가 있기에 이를 개선하기 위해 사용한다.
• 양성 샘플과 음성 샘플로 현재 데이터를 나누고 양성샘플은 현재 계산에 관심이 있는 데이터이고 음성데이터는 나머지 관심이 적은 데이터를 말한다. 이때 소프트맥스함수에서 모든 클래스를 계산하는 대신 음성 샘플 몇개를 사용하여 학습할 수 있도록한다.
• 즉 실제 양성 샘플들과의 정확도는 높히면서 음성들과의 정확도는 낮추는 방향으로 최적화하게 된다.

• 앞에 있는 양성샘플의 내적값은 크게하고 뒤에있는 음성샘플과의 내적값은 최소화하는 것을 목표로 한다.
• 결과적으로 이 loss function을 gradient descent를 사용하여 최적화시키면된다.