[Network Science]15.Cascades in Networks
- 이전에 epidemic에서는 전염병에 대한 전파를 다루었다면 이 장에서는 일반적인 전파 그 중에서도 특히 각 노드가 의사결정을 하는데에서 오는 전파에 대해서 다룰 것이다.
- 전염병의 경우는 특정 노드의 의사에 상관없이 이웃노드에 따라 해당 노드의 상태가 변화하는 것이라면 이곳에서는 이웃노드의 상태에 따라 특정 노드가 주도적으로 상태를 변화하는 모델을 설명할 것이다.
- 대표적인 예시로 내 주변사람들이 휴대폰을 삼성에서 애플로 기종을 변경하였을 때 나도 애플로 기종을 변경하고 싶은 마음이 클 것이다. 이러한 현상들을 설명한다.
Network Coordination Game
- 위에서의 휴대폰을 예시로 기본적인 게임이론으로 위 현상을 설명해보겠다.
- 우리가 가장 기본적으로 생각할 수 있는 아이디어는 내 친구 중 절반 이상이 사용하는 기종을 내가 사용하면 좋은 것이 아닌가?라는 대답을 할 수 있다. 물론 어느정도 일리있는 말이다.
- 하지만 조금만 더 상세하게 들어간다면 친구와 내가 서로 같은 기종을 사용하였을 때 만족감을 얻는다라고 한다면 그 같은 기종이 애플이냐 삼성이냐에 따라 만족감은 다를 것이다. 예를 들어 친구와 서로 애플을 사용하였을 때 에어드랍이라는 기능을 상호 사용할 수 있다면 서로 삼성을 사용하는 것보다 더 만족감이 높을 수 있다.
- 이를 일반화 하면 다음과 같이 나타낼 수 있다.
- 서로 같은 기종을 사용하면 서로 점수를 얻지만 서로 다른 기종을 사용하였을 때 benefit은 존재하지 않는다.
Threshold model
- 위에서 정의한 규칙으로 임계값을 찾아보도록 하겠다.
a×p>b×(1−p)p≥a+bb
- p가 a를 사용하는 사람의 비율이라고 하였을 때 우리가 a를 사용할 임계값을 위와 같이 정의할 수 있다.
- 만약 a와 b가 동일하다면 임계값은 21이 될 것이고 a가 크다면 그 임계값은 줄어들게 될 것이다. 즉 만족감이 높기 때문에 조금 덜 적은 사람이 사용하더라도 그만큼 강력하다라는 것이다.
Independent Cascade Model
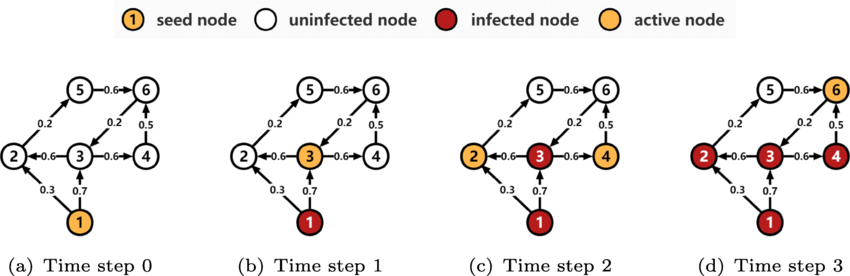
- 이는 우리가 이전에 배웠던 전염병을 다루는 SI, SIR모델과 비슷하다.
- 하지만 가장 큰 차이점이 있다면 감염된 노드는 전파를 딱 1회만 한다라는 것이다. 일반적으로 SI,SIR모델은 특정노드가 전염될 때까지 계속 전파를 하게된다. 그러한 측면에서 전파를 딱 1회만하는 SIR모델이라고 볼 수 있고 이때 R은 전염되었지만 전파는 불가능한 상태라고 볼 수 있다.
- 또한 이때 전파될 확률은 각 edge마다 다르다. pv,w는 서로 다른 노드 사이에 전파가 이루어질 확률이고 이는 각 노드 간의 결합도가 다를 것임을 가정하고 가중치를 다르게 준 것이다. 예를 들어 내가 친한 친구의 상태가 나에게 미치는 영향과 단순히 얼굴만 알고 지내는 친구가 나에게 주는 영향은 다를 것이다.
- 위에서 본 Threshold model에서는 이러한 가중치가 없다라고 가정하였고 이를 보완해준 모형이다.
- 이 모델의 특징은 전염병처럼 확률적으로 감염이 된다라는 것이다. 임계치에 상관없이 독립적으로 감염이 진행되고 아무리 확률이 높아도 감염이 되지 않을 수도 있다.
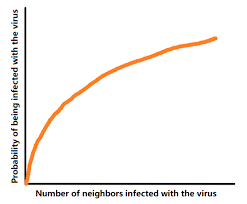
P(n)=1−(1−p)n
- 다음과 같이 감염될확률 P(n) 을 나타낼 수 있고 이때 p는 주변 노드로 부터 감염될 확률이다. (여기서는 모든 edge에 같은 가중치가 부여됐음을 가정) n은 neighbor의 수이다. 즉 감염된 neighbor가 많을수록 일반적으로 감염확률이 올라가고 이는 초반에 급격하게 증가하다가 점점 기울기가 낮아지는 것을 볼 수 있다.
Linear Threshold Model
- 이전에는 독립적인 확률로 접근을 하였다면 이 모형에서는 특정 값을 넘기게되면 활성화(1) 못넘기면 비활성화(0)로 이분화된 관점에서 설명하는 모델이다.
- 특정 임계값 각 노드 i에는 임계값 θi가 존재하고 주변의 활성화된 노드들의 가중치의 합이 임계값을 넘어가면 해당 노드도 활성화가 된다.
active j∈N(i)∑wji>θi
- 이 모형에서도 서로 다른 두 노드간의 가중치는 다를 수 있다는 것을 가정한다.
Random Graph
- 이 모델을 random graph에 적용시켜보면 재미있는 결과를 얻을 수 있다.
Depending on z(Average of neighbor)
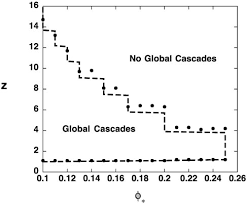
- 가로축은 임계치이고 세로축은 random graph에서 평균 neighbor수이다. 이때 그래프를 살펴보면 global cascade가 발생하는 지점은 다음 아래부분과 같다.
- 이때 z값이 너무 크게되면 수용해야하는 주변노드가 많아지므로 활성화되는 조건이 어려워진다. 따라서 적당한 값의 z가 주어질 때만 활성화가 될 수 있다.
- 또한 임계치가 너무 높아지게될 때도 활성화되기 위한 조건이 어려워지므로 그래프는 오른쪽 아래로 더 낮아지게 된다.
Depending on sigma
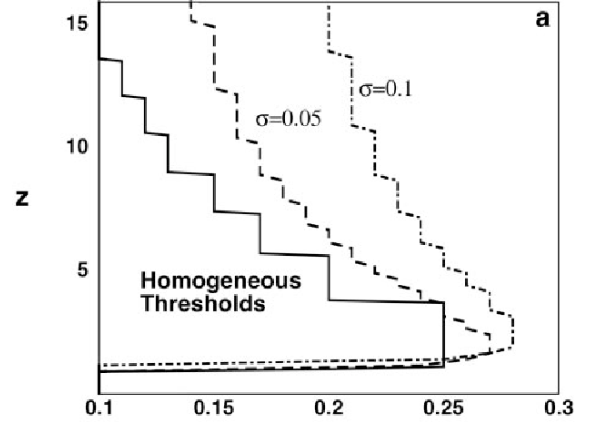
- 시그마는 임계치의 분포의 표준편차를 나타낸다. Homogeneous는 모두 동일한 활성화 임계치를 가진다는 뜻이다.
- 이때 이 분포가 넓을수록 임계치가 낮은 노드가 존재한다는 뜻이고 그러한 노드들이 도화선 역할을 할 수 있으므로 더 많은 경우에 활성화가 될 수 있다.
- 하지만 너무 큰 임계치를 가지게되면 특정노드들은 활성화되기 너무 힘드므로 적당한 σ일 때만 활성화가 가능하다.
Influence Maximization Problem
- 이전까지 전파에 영향을 미치는 다양한 요소를 보았다. 이번에는 초기 시드에 대해서 알아본다. 동일한 그래프에서 초기에 어떤 노드에서 시작하였는지에 따라 최종 전파되는 결과에 큰 영향을 미치게된다.
- 단순하게 생각하여 바이럴마케팅에서 인플루언서가 홍보하는 것과 팔로워가 10명인 사람이 홍보하였을 때 결과는 매우 다를 것이다. 따라서 우리는 graph에서 이러한 전파가 최대화가 될 수 있는 초기 집합을 찾는 것은 매우 중요한 문제이다.
- 이때 A0는 초기 시드집합이고 σ(A0)은 이 초기 시드집합으로 최종적으로 전파할 수 있는 노드의 수이다. 즉 우리는 σ(A0)를 최대화할 수 있는 A0를 찾는 것을 목표로한다.
- 물론 이것을 정확하게 찾는 것은 NP-hard 문제이기에 그리디 알고리즘을 이용하여 구할 수 있다.
Submodular Functions
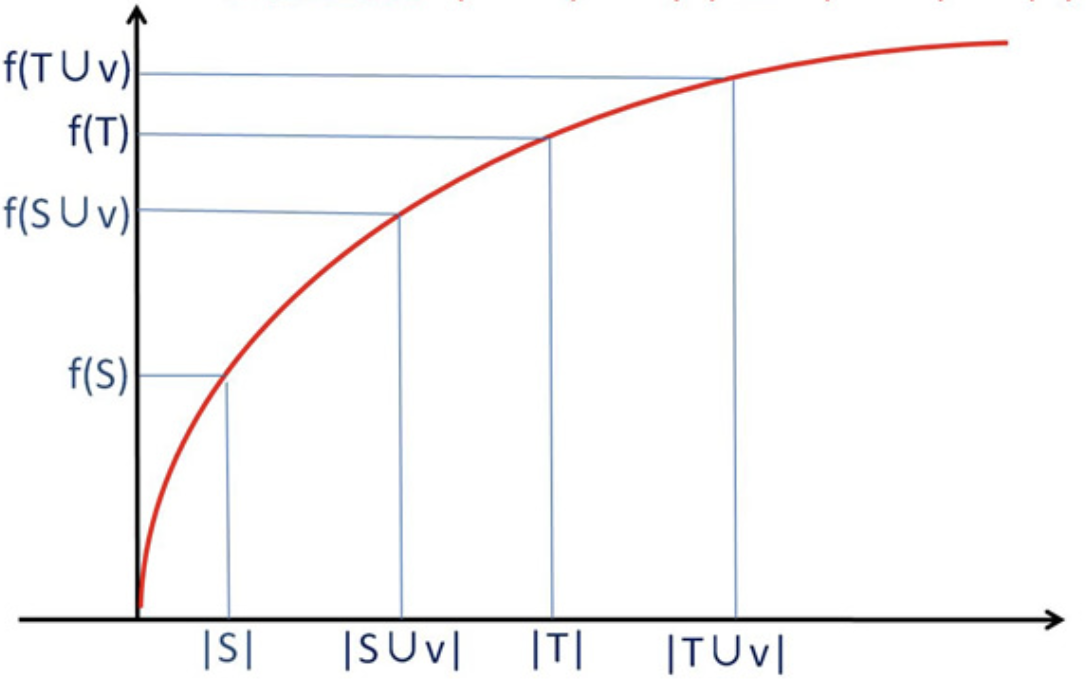
- S⊂T라고 했을 때 f(S∪{v})−f(S)≥f(T∪{v})−f(T)로 표현할 수 있다.
- 기존 집합에 노드를 추가하였을 때 전파는 더 커질 것이고 초기에는 빠르게 증가하지만 집합이 커짐에 따라 그 속도는 점점 감소하는 단조증가 함수 형태가 될 것이다.
Greedy Algorithm
- 이 문제는 NP-hard문제이기에 그리디 알고리즘을 사용하여 해를 구해야한다. 한가지 흥미로운 사실은 그리디 알고리즘으로 해를 구해도 일정 이상의 정확도를 보장한다는 것이다.
f(S)≥(1−e1)f(S∗)
- S∗는 해당 그래프에서 최적의 집합이다. 하지만 우리는 이것을 구할 수 없기에 그리디 알고리즘을 이용하여 S를 구할 수 있고 이때 이것의 성능은 최적의 성능의 0.629 이상임이 보장된다.
Algorithm
- 초기 집합 S는 공집합으로 설정하고 시드집합 크기는 k로 설정한다
- 매 시행마다 σ(S∪{u})−σ(S)를 최대화 하는 u를 찾아 해당 집합에 추가시킨다
- 집합의 크기가 k가 될 때까지 반복한다.
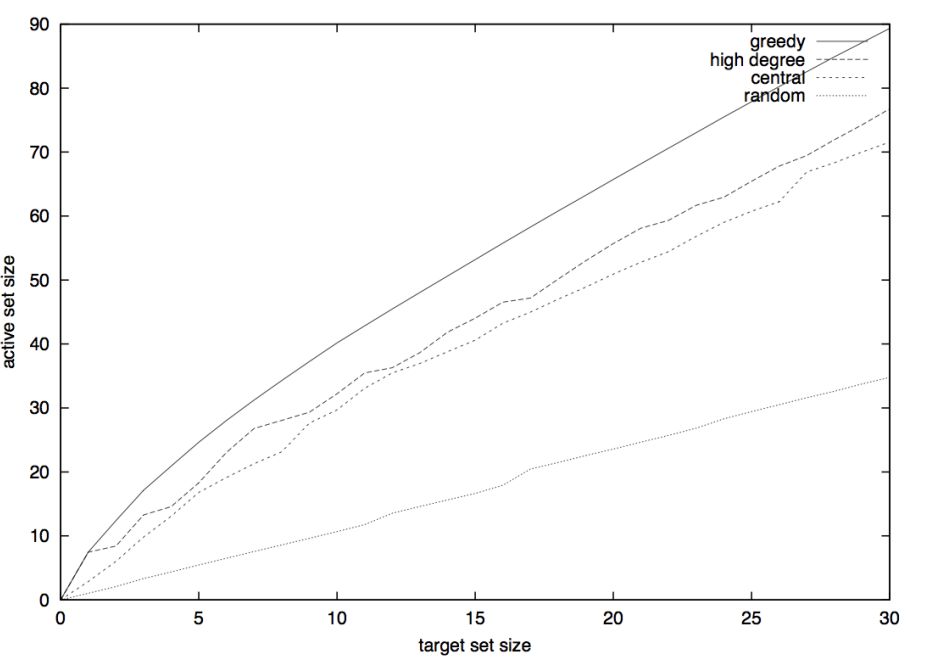
- 실제로 그리디 알고리즘의 성능이 다른 휴리스틱 알고리즘들 보다 좋게 나오는 것을 확인할 수 있다. random graph보다는 약 3배정도 좋다.
- 하지만 그리디 알고리즘 조차도 시간복잡도가 크기 때문에 비용을 줄이는 다양한 알고리즘들이 등장한다.






