[Network Science]4. Network Models

YongUk·2025년 1월 27일
GNNGraphnetwork science

Graph Theory

목록 보기
6/17
  • 실제 세계의 그래프를 표현 혹은 분석하기 위해 실제와 비슷한 그래프를 만드는 것을 목표로 하고 있고 이전에 그 중 하나인 Random Graph를 보았다.
  • 하지만 이는 degree distribution과 clustering coefficient를 만족하지 못하기 때문에 좋은 모델은 아니었다. 또한 중요한 것은 실제 세계에서는 노드들이 점점 늘어나는 반면 Random Graph에서는 고정된 노드 개수 값이 존재했다.
  • 이러한 단점들을 보완하기 위한 모델들이 존재하게 된다.

BA model(Barabasi and Albert)

  • = Preferential attachment model
  • Start : t=0일 때 n0n_0개의 노드와 각각 m0m_0개의 edge를 가지고 시작한다.

Features

  • BA 모델은 크게 2가지를 특징으로 한다.
  1. Growth
    • 단위시간당 노드가 1개씩 추가되게 된다. 각 노드는 m개의 노드들과 연결된다
    • t=tit = t_i 일때 node는 n0+tin_0 + t_i 이고 edge는 m0+timm_0 + t_im 이 된다.
  2. Preferential attachment
    • 새로 추가되는 노드와 기존의 노드가 연결될 확률은 기존의 노드의 degree에 따라 다르다.
    • 기존의 노드의 degree가 클수록 새로운 노드를 받아들일 확률이 높아진다.
      Π(ki)=ki∑jkj\Pi(k_i) = \frac{k_i}{\sum_j k_j}

Calculating Degree

dki(t)dt=mΠ(ki)=mki∑jkj=mki2mt=ki(t)2t\frac{dk_i(t)}{dt} = m\Pi(k_i) = m\frac{k_i}{\sum_j k_j} = \frac{mk_i}{2mt} = \frac{k_i(t)}{2t}
  • ki(t)k_i(t)는 degree가 t에 따라 변한다는 것을 명시적으로 나타낸 것이다.
  • 시간에 따른 degree 변화량을 계산해 보았을 때 한 timestamp에 총 m개의 노드 연결이 있고 그 것에 노드 i의 확률분포를 곱해 기댓값을 이용할 수 있다.
  • 위에서 구한 등식을 통해 아래과 같이 나타낼 수 있을 것이다.
∫mki(t)dkiki=∫titdt2t\int^{k_i(t)}_m \frac{dk_i}{k_i} = \int^t_{t_i} \frac{dt}{2t}
  • 이때 tit_i는 노드 i가 생성된 timestamp를 의미하고 초기에는 m개의 edge로 시작하기 때문에 ki(ti)=mk_i(t_i) = m으로 나타낼 수 있다.
  • 위 적분식을 전개하면 아래와 같이 정리가된다.
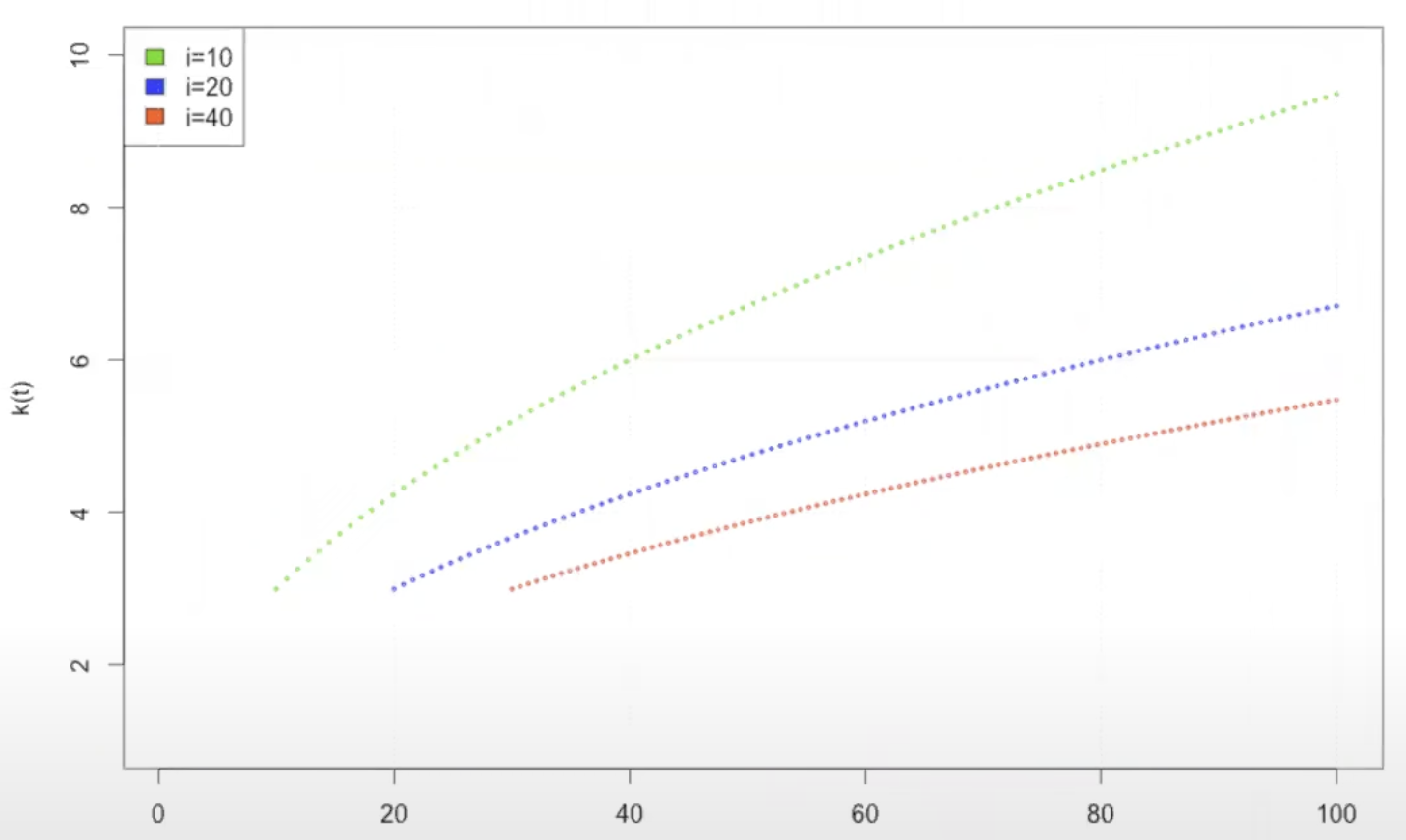
ki(t)=m(tti)12k_i(t) = m\left(\frac{t}{t_i}\right)^\frac{1}{2}
  • 여기서 우리가 알 수 있는 것은 Node의 Degree는 시간에 따라 제곱근으로 증가한다는 것과 노드의 출현 시기가 빠를수록 같은 timestamp에 Degree 값은 더 크다는 것이다.
dki(t)dt=m2tti\frac{dk_i(t)}{dt} = \frac{m}{2\sqrt{tt_i}}
  • 또한 다음과 같이 시간에 따른 degree 변화량을 구해보면 변화량은 점점 줄어드는 것을 확인할 수 있다. 그 이유는 경쟁할 노드의 수가 점점 많아지기 때문이라고 생각하면 좋다. 하지만 그보다 중요한 점은 같은 timestamp에 일찍 등장한 노드의 변화량이 더 크다는 것이다.
  • 즉 일찍 등장한 노드는 늦게 등장한 노드보다 같은 timestamp에서 항상 degree값이 크고 또한 degree 변화량(성장 속도)도 크다.

Degree Probability

  • degree의 확률분포를 구하기 위해 누적확률 분포를 이용한다.
  • 우리는 현재 timestamp에 따른 degree 값을 가지고 있다. 이를 degree distribution으로 만들기 위해서는 degree에 따른 노드의 개수로 바꾸어야한다.
  • k′≤kk^{\prime} \le k를 만족하는 노드를 찾는다
m(tti)12≤k    →    ti≥m2k2tm\left(\frac{t}{t_i}\right)^\frac{1}{2} \le k\ \ \ \ \rarr \ \ \ \ t_i \ge \frac{m^2}{k^2}t
  • 다음과 같이 tit_i 이후에 생성된 노드만 대상이고 그 이전에 생성된 것들은 부등식을 만족하지 않는다
F(k)=P(k′≤k)=n0+t−m2tk2n0+t≈1−m2k2F(k) = P(k^\prime\le k) = \frac{n_0+t-\frac{m^2t}{k^2}}{n_0+t} \approx 1 - \frac{m^2}{k^2}
  • 최종적으로 다음과 같이 유도하여 누적확률분포를 얻을 수 있다.

Degree Distribution Function

P(k)=ddkF(k)=2m2k3P(k) = \frac{d}{dk}F(k) = \frac{2m^2}{k^3}
  • 누적확률분포를 미분하여 확률분포를 얻을 수 있고 다음 결과를 통해 우리가 아는 Power law Distribution Funtion인 Ck−γCk^{-\gamma}의 형태를 띄고 γ=3\gamma = 3 인 모습인 것을 알 수 있다.
  • 특이한 점은 시간에 의존받지않는 함수가 생성된다는 것이다.

Conclusion

  • Power law distribution : P(k)=2m2k3P(k) = \frac{2m^2}{k^3}이므로 만족한다
  • Average path length : ⟨L⟩∼log⁡(N)log⁡(log⁡(N))\langle L \rangle \sim \frac{\log(N)}{\log(\log(N))} 으로 나타낼 수 있고 만족한다
  • Clustering coefficient : C∼N−0.75C \sim N^{-0.75} 굉장히 작은 수치이고 만족하지 않는다

Growing Random Graph

  • 이는 BA 모델에서 preferential attachment를 뺀 것, 혹은 random graph에 growing을 넣은 것과 같은 개념으로 생각할 수 있다.

Features

  1. Growth

  2. Attachment Unifromly at Ramdom

    • BA 모델과 달리 시간이 지나도 각 노드에 연결될 확률은 동일하다
    Π(ki)=1n0+t−1\Pi(k_i) = \frac{1}{n_0+t-1}
    • 이전과 달리 모든 노드 i에 대해 같은 확률이 적용되는 것을 볼 수 있다.

Degree

ki(t)=m(1+ln⁡(ti))k_i(t) = m\left(1+\ln\left(\frac{t}{i}\right)\right)
  • 이전에 한 방법과 동일하게 구해보면 다음과 같은 식을 얻을 수 있고 이전에는 (ti)\left(\frac{t}{i}\right)에 대해 제곱근으로 증가하였지만 현재는 로그로 증가하며 훨씬 작아진 것을 알 수 있다.

Degree Distribution Function

P(k)=e1−kmmP(k) = \frac{e^{1-\frac{k}{m}}}{m}
  • 여기서 볼 수 있듯이 지수분포의 형태로 나타내지기 때문에 BA모델을 사용했을 때 보다 그래프가 훨씬 더 빠르게 감소한다는 것을 알 수 있다. 즉 BA모델에서는 Growth도 중요하지만 Preferential Attachment가 없으면 소용이 없다는 것을 알 수 있다.

Power law distribution을 따르는 다른 모델

  • Growth
  • Link selection : 노드가 아닌 링크를 임의로 선택한 후 양극단의 노드 중 하나를 무작위로 선택한다.
qk=kpk⟨k⟩q_k = \frac{kp_k}{\langle k \rangle}
  • pkp_k : k 노드에 해당하는 노드들의 차수 분포
  • kk : 노드 차수
  • kpkkp_k : 임의로 edge를 선택했을 때 degree가 k인 노드가 걸릴 확률
    • degree에 비례하고 해당 차수의 노드의 개수에 비례한다
  • ⟨k⟩\langle k \rangle : qkq_k의 총합을 1로 정규화하기위해 사용됨

Copying model

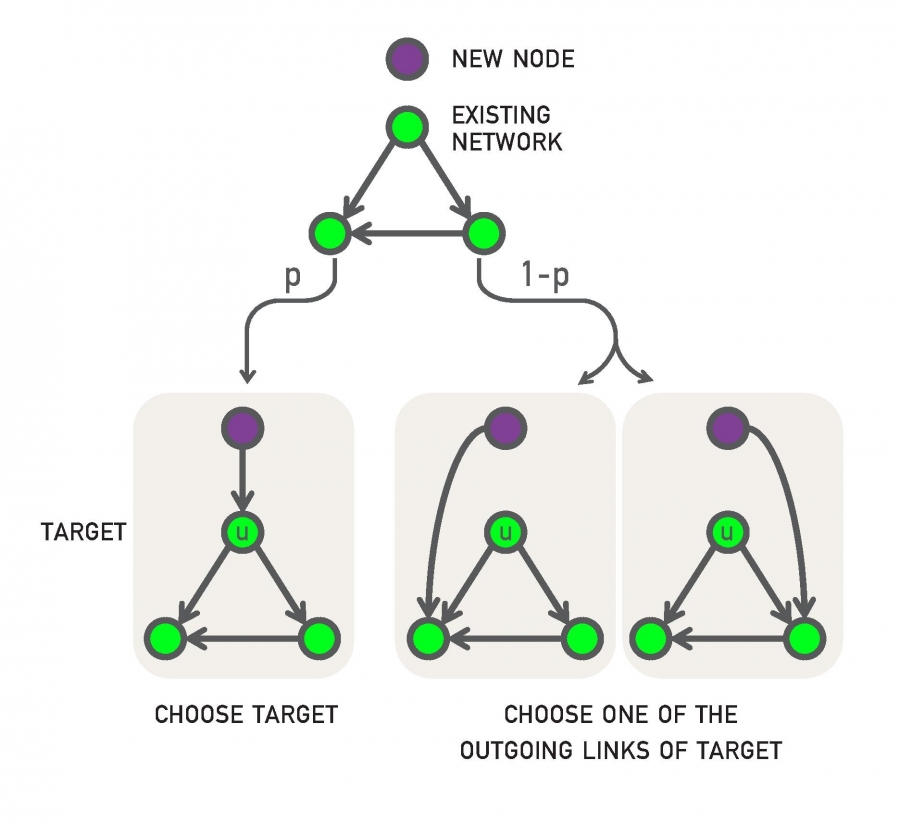
  • Random Connection : p의 확률로 노드 u와 연결됨
  • Copying : 1-p의 확률로 u의 outgoing edge의 반대편에있는 노드 중 하나와 연결됨
Π(k)=pn+(1−p)k2m\Pi(k) = \frac{p}{n}+(1-p)\frac{k}{2m}
  • pn\frac{p}{n} : p의 확률로 n개의 노드 중 하나에 연결됨
  • (1−p)k2m(1-p)\frac{k}{2m} : (1-p)의 확률로 전체 in-degree 중 자신에게 들어오는 k개 중 하나로 연결됨

Conclusion

  • 이 두 모델 모두 k에 대해 선형적으로 증가하는 확률을 가지고 있다

WS model(Watts and Strogatz)

  • Preferential Attachment 모델의 경우는 실제로 power law distribution과 small wolrd의 특성은 따르지만 clustering coefficient는 따르지 않는다. 따라서 여기서 초점을 맞춘 모델을 살펴본다

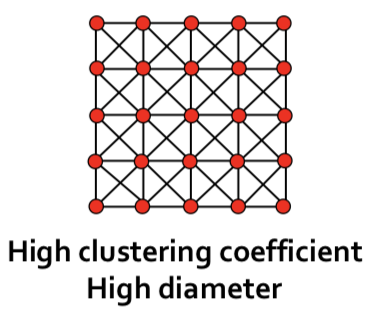
  • 위 그래프는 굉장히 clustering coefficient가 높다고 볼 수 있다. 하지만 small world의 특성은 가지고 있지 않다. 이러한 특성을 만족시키기 위해 약간의 수정이 필요하다.

Algorithm

  1. n개의 vertex와 각각 k개의 edge로 시작한다. + 격자 형태로 연결한다(clusering coefficent 증가)
  2. 각각의 vertex의 오른쪽에 있는 edge를 p의 확률로 다른 노드에 연결(diameter를 줄인다)

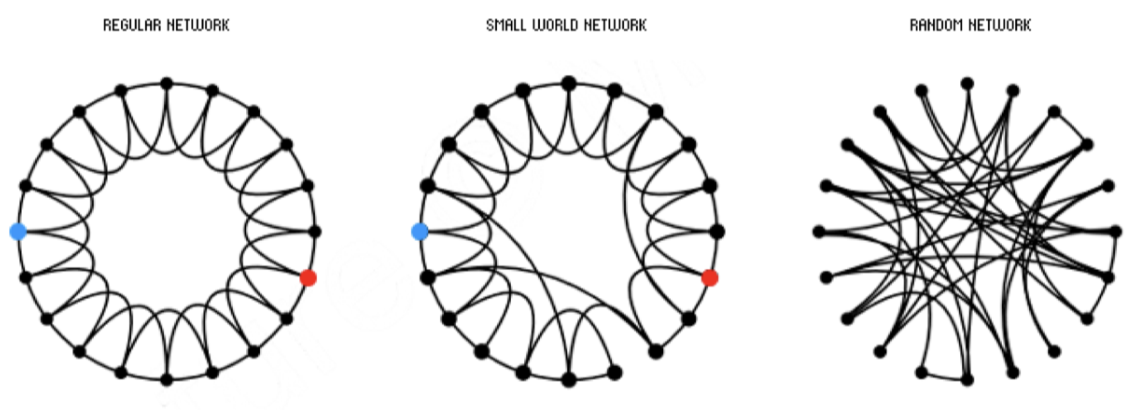
- 이때 p=0이면 격자 그래프가 유지되고 p=1이면 random graph가 된다
- 이 적정선을 유지한다면 clustering coefficient와 small world의 특성을 모두 챙길 수 있다.

Small World

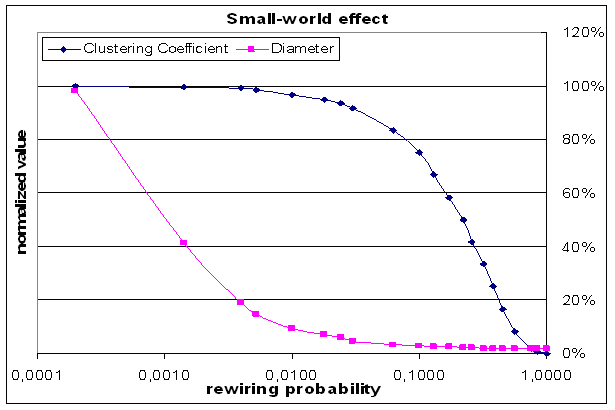
  • 둘은 서로 trade-off 관계에 있기 때문에 small world와 clustering coefficient 특성을 모두 챙기기 위해서는 적당한 경계선이 필요하다.
  • 위 그림에서보면 0.01 정도의 선에서 clustering coefficient는 많이 잃지 않으면 diameter는 많이 줄인 것을 볼 수 있다.

Conclusion

  • Power law distribution : 만족하지 않는다
  • Average path length : 만족한다
  • Clustering coefficient : 만족한다

Summary

  • BA model은 clustering coefficient를 만족하지 않는 반면 WS model은 power law distribution을 만족하지 않는다. 각자 장점이 있지만 둘을 따로 사용하였을 때는 실제 세계를 전부다 묘사하지는 못한다.
  • 즉, 이러한 기초가 되는 다양한 모델을 조합, 응용하여 실제 세계를 다룰 수 있는 최대한 완벽한 모델을 만드려고 노력하는 것이 중요하다.
profile
YongUk
이전 포스트

[Network Science]3. Random Graphs

다음 포스트

[Network Science]5. Node Centrality and Ranking on Networks

0개의 댓글