[Network Science]5. Node Centrality and Ranking on Networks

YongUk·2025년 2월 1일

GNN Graph network science

Graph Theory

목록 보기

7/17

Node Centrality

우리는 이 그래프에서 어떤 노드가 중심인지 혹은 어떤 노드가 중요한지 알 수 있을까? 아마도 원의 크기를 통해 유추할 수 있을 것이다. 하지만 만약 아래와 같은 그래프가 들어온다고 생각하여보자

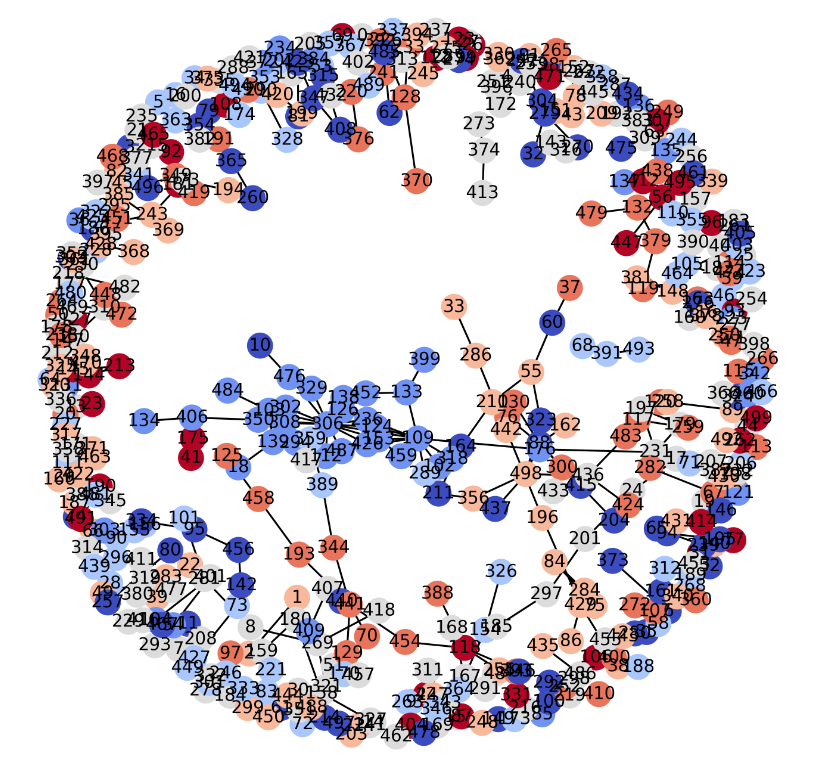
어떤 노드가 다른 노드들보다 중요한지 한번에 알 수 없을 것이다.
즉 우리는 이와 같은 그래프들에서 중요한 노드를 찾아내어 맨 위에 있는 그래프와 같은 그래프를 만들 수 있어야 한다.
그렇다면 무엇이 중요한 노드 혹은 중심 노드일까?
우리는 이 중요하다의 기준을 정해놓아야한다.
이와 같이 미리 중요하다라는 기준을 정해놓은 것은 노드 중심성 지표라고 하고 대표적인 몇가지 예시를 살펴보자

Degree Centrality

연결 중심성이라고 불리는 것이다.
이는 말 그대로 degree 즉 현재 노드의 이웃의 수를 기준으로 중심 노드를 찾는 것이다.
"degree가 높다 == 중요하다" 라는 개념으로 degree가 가장 높은 노드가 가장 중요한 노드가 된다.

C_D(i) = k(i) = \sum_jA_{ij}

인접행렬을 이용하여 i번째 노드의 연결중심성을 구하는 공식이다.
이 간단한 공식에서 조금 생각해보면 만약 10001개의 노드가 있고 1개의 중심 노드에 10000개의 노드가 연결되어 있거나 5개의 노드가 있고 1개의 중심노드에 4개의 노드가 연결된 상황을 생각해보자.
아래와 같은 모습을 생각해보자

그렇다면 전자의 경우 중심 노드의 연결중심성 값은 10000일 것이고 후자는 4일 것이다.
하지만 우리는 이 두 그래프의 생김새가 동일하고 중심성의 정도도 동일할 것이라 생각할 수 있다.
즉, 그래프의 스케일에 따라서 지표가의 차이가 크게 나므로 다른 그래프와의 비교를 위해서라도 이를 정규화 시킬 필요가 있다.

C^*_D(i) = \frac{k(i)}{N-1}

정규화 시킨 공식은 다음과 같고 현재 노드를 제외한 N-1개의 노드로 나누어 주는 것을 알 수 있다.
이를 통해 중심성이 높은 노드의 경우 중심성 값이 1에 가까울 것이고 낮은 경우 0에 가까워질 것이다.
하지만 이 중심성의 경우 각 노드의 너무 지역적인 부분만 바라보고 전체적인 부분은 보지못한다는 큰 단점이 존재한다.

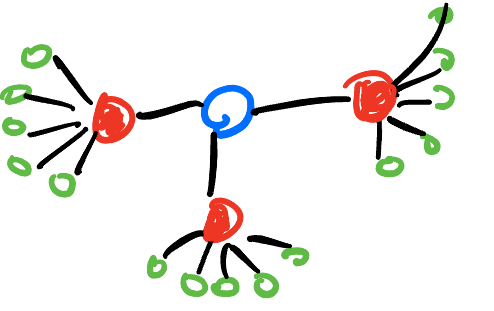
위와 같은 그림을 생각해보자.
이정도 그래프는 우리가 쉽게 파란색이 중심이라 생각하겠지만 연결중심성은 빨간색이 중심이라고 말한다.
따라서 굉장히 단순하나 이러한 국지적인 관점만 본다는 문제를 지니고있다.

Closeness Centrality

다음은 근접 중심성이다.
위 근접 중심성은 한 개의 노드에서 다른 모든 노드에 도달할때 걸리는 최단 거리의 합이다.
이는 한 노드에서 다른 모든 노드까지의 거리를 고려한다는 점에서 아까 위에서 본 국지적인 관점을 해결할 수 있는 방식이다.

C_C{i} = \frac{1}{\sum_jd(i,j)}

모든 최단거리의 합의 역수이고, 역수인 이유는 중심성이 클수록 중심이라는 일관성을 위해 거리의 합이 적을수록 중심성이 높도록 하기위함이다.

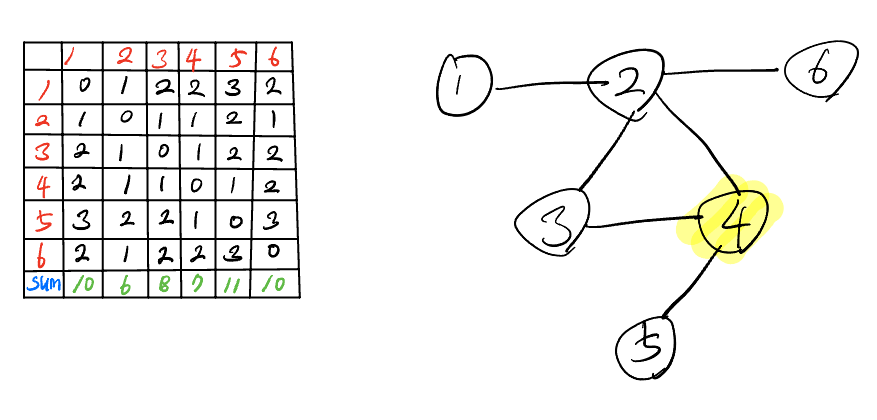
위의 예시를 살펴보면 노드와 노드간의 모든 최단거리를 구하고 이에 대한 합이 가장 적은 노드를 순서대로 중심성이 높다라고 판단할 수 있다. 이 또한 정규화가 가능한데 다음과 같다.

C_C^*{i} = \frac{N-1}{\sum_jd(i,j)}

하지만 이 중심성 지표는 연결요소가 여러 개라 노드간의 거리가 존재하지 않는 노드가 존재할 경우 사용할 수 없다. 두 노드 상의 거리가 발산하기 때문이다.

Betweenness Centrality

이는 매개 중심성이라 불린다. 먼저 공식을 살펴보면

C_B(i) = \sum_{s\ne t \ne i}\frac{\sigma_{st}(i)}{\sigma_{st}}

위와 같고 여기서 i의 중심성을 구하기 위해서 s,t를 사용한다.
공식을 자세히 살펴보면 $\sigma_{st}$ 는 s와 t의 최단 경로의 개수로 해석할 수 있고 $\sigma_{st}(i)$ 는 s와 t의 최단 경로 중 i를 지나는 것의 개수라고 볼 수 있다.
즉 i의 매개 중심성을 구하기 위해 나머지 모든 정점의 조합으로부터 최단거리의 개수를 구하고 그 중 i를 지나는 최단거리의 개수의 비율의 합이 된다.
이 또한 정규화 시킬 수 있는데

C_B^*(i) = \frac{2}{(N-1)(N-2)}\sum_{s\ne t \ne i}\frac{\sigma_{st}(i)}{\sigma_{st}}

여기서는 합하는 개수가 $N-1$ 이 아니라 자신을 제외한 정점의 조합들이기 때문에 총 $\frac{(N-1)(N-2)}{2}$ 가 되고 이를 나눠주어 정규화 시킬 수 있다.

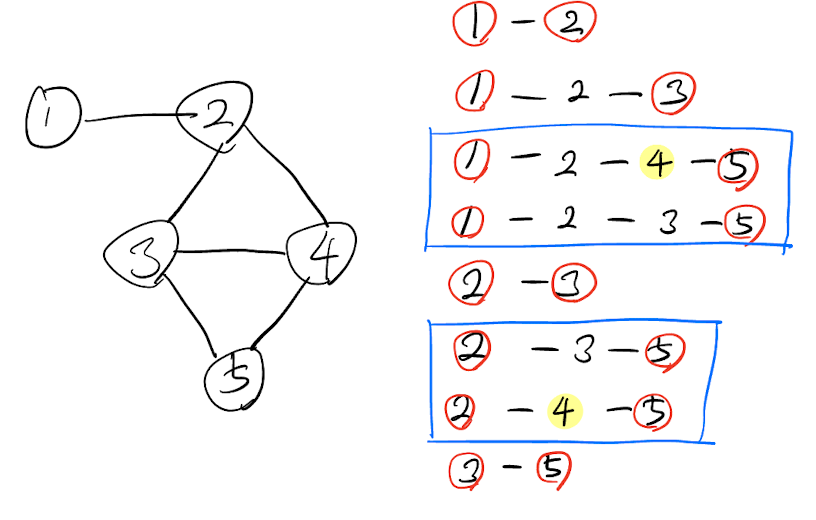
4의 매개 중심성을 구한다고 했을때 다음과 같고 이때 0.5 + 0.5로 매개 중심성은 1이 되게 된다.

Eigenvector Centrality

고유벡터 중심성
선형대수학에 나오는 고유벡터를 사용하고 중심성을 구하는 방식이다.
이 중심성의 배경을 생각하자면 위에서 본 중심성은 단순히 개수라는 수치를 고려하였다.
하지만 쉽게 생각해보면 SNS에서 팔로워가 많은 사람들은 보통 인플루언서라고 칭한다.
하지만 요즘 SNS 팔로워를 늘리기위해 의미없는 계정을 사서 인위적으로 팔로워를 늘리는 사람들을 볼 수 있다. 하지만 과연 이런 사람들이 높은 중심성은 가진 사람이라고 할 수 있을까?
이러한 문제를 해결하기위해 단순히 연결 개수가 아닌 연결된 노드의 중심성까지 고려해야한다.
즉 고유벡터 중심성에서는 각 연결된 노드에 가중치를 부여하여 계산할 수 있다.
이전에는 각 노드의 가중치가 모두 동일하다라고 생각할 수 있다. 하지만 여기서는 각 노드의 가중치가 다를 수 있다는 전제를 가질 수 있다.

v_i = \sum_j{A_{ij}v_j}

이는 현재 노드의 중심성을 구할 때 인접노드의 가중치의 합을 사용한다. 하지만 공식에서 볼 수 있다시피 이 방식은 재귀적인 절차를 요구한다.
하지만 현재 공식에서 재귀적으로 계속 진행할 경우 값은 지속적으로 발산한다는 것을 알 수 있을 것이다.
예를 들어 1,2,3번 노드가 삼각형의 형태로 서로 연결되어있다고 생각하자. 그리고 초기의 가중치는 모두 1이다.

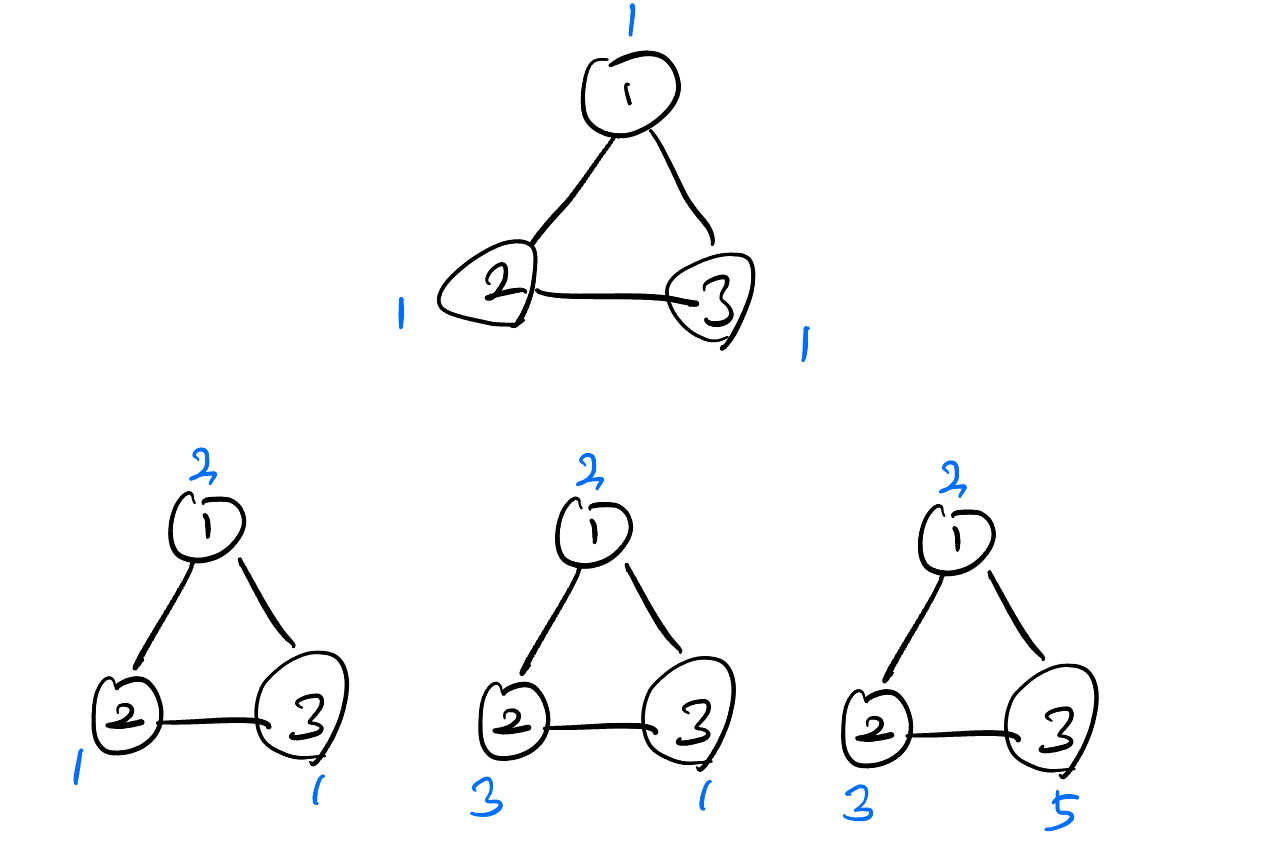
위에가 초기이고 아래가 한번의 사이클을 진행한 상태이다. 이와 같은 과정이 재귀적으로 반복되면 값은 끝없이 발산하게 될 것이다. 이때 우리는 적당한 $\lambda$ 를 사용한다.

v_i = \frac{1}{\lambda}\sum_j{A_{ij}v_j}

이 수렴하는 적당한 $\lambda$ 가 있다라고 말하고 이 $\lambda$ 를 고윳값이라고 부른다. 이 식을 조금 일반화 시키면
$Av = \lambda v$ 가 되고 이는 우리가 일반적으로 알고있는 고윳값을 구하는 공식이 된다.
이곳에서 우리는 가중치에 해당하는 $v$ 즉 고유벡터를 구하면 된다.
이는 선형대수학에서 배운 고윳값 구하는 공식을 사용하면 되고 이때 eigenvalue가 가장 클 때의 eigenvector를 중심성으로 사용한다.
eigenvalue가 가장 크다라는 것은 일반적으로 변환의 영향력이 가장 크고 혹은 중요한 노드의 중요성이 더 강조될 때를 의미한다.

Katz Centrality

Eigenvector의 단점을 보완한 Katz Centraility와 많은 다른 알고리즘이 존재한다.
- Katz는 Egienvector Centrality에서 어떠한 노드도 0인 가중치를 갖지않도록 기본값을 정해주는 알고리즘이다.
- directed graph에서 고립된 노드들 같은 경우에는 가중치가 업데이트 되지 않는 경우가 발생할 수 있다. 따라서 pagerank에서의 텔레포트와 유사하다고 볼 수 있다.
eigenvector centrality의 식을 보면 간단히 $x^{(t+1)} = Ax^{(t)}$ 로 나타낼 수 있다.
이 식에서 0이되지 않도록 상수항을 정의해주고( $\beta$ ) 노드 간의 거리에 따라 가중치를 부여하는 항( $\alpha$ )을 하나 추가해줄 수 있다.
- eigenvector centrality 에도 가중치의 역할을 하는 $\lambda$ 가 있다고 생각할 수 있지만 그것은 고유벡터 방향을 따르기 때문에 온전히 멀리있는 노드의 가중치를 고려하는 것으로 보기 힘들다. 따라서 그러한 특수한 역할을 하는 것이 $\alpha$ 이다.
- 또한 하이퍼파라미터로 값을 조절할 수 있기에 거리에 따른 노드의 가중치를 어떻게 적용할지 조절할 수 있다.

x^{(t+1)} = \alpha Ax^{(t)} + \beta

정리

추가적으로 위와 같은 특징들 때문에 Closeness Centrality를 통해 중심성이 높다고 판단되는 노드는 일반적으로 클러스터의 중심이 된다.
Betweenness Centrality는 클러스터의 연결부분에 위치하게되고 Eigenvector Centrality는 일반적으로 서로 밀집된 형태를 지니게 된다.

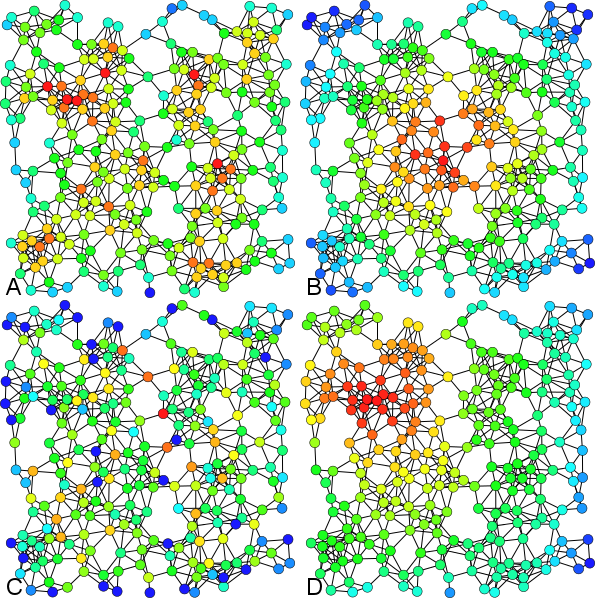
A : Degree
B : Closeness
C : Betweenness
D : Eigenvector

Directed Graph

이때까지 본 내용은 Undirected Graph에서 통용되는 이야기일 것이다. 하지만 Directed Graph에서는 우리가 알다시피 Symmetric 하지 않기 때문에 위와같이 중심성을 구하는데에 있어서서는 조금 신중할 필요가 있다.

Strongly Connected Component

Directed 그래프는 방향이 존재하기때문에 A→B는 가능하지만 B→A는 불가능한 경우가 발생할 수 있다.
그렇기에 Connected Component를 구분할 필요가 있는데 이때 A→B와 B→A가 가능한 원소들끼리의 부분집합을 Strongly Connected Component라고 말한다

Aperiodic Graph

그래프의 비주기성이라고 부르는데 그래프가 비주기성을 가질 때 장점들이 많기 때문에 해당 특성의 만족 여부를 아는 것이 중요하다.
알고리즘
- 가정 : Strongly Connected Component로 이루어져있다.
1. 각각의 노드에서 출발하여 가능한 모든 경로의 길이를 구한다. (DFS이용)
2. 각 경로들의 최대공약수가 1이면 비주기성을 만족한다고 볼 수 있다.
만약 그래프가 주기성을 가지는 경우 self loop를 하나 추가하면 최대공약수는 1로 통일된다.

PageRank

구글의 검색엔진 알고리즘으로 매우 유명하다.
구글의 각 페이지들이 하이퍼링크로 연결되어있는 관계를 통해 각 페이지의 영향력 및 중요도를 평가할 수 있는데 이때 Random Surffer의 원리를 사용하고 이는 실제 사람이 웹페이지를 돌아다니는 것을 토대로 수학적 모델링을 한 것이다.
- 예를 들어 어떤 페이지에서 링크를 눌러 다른페이지로 가거나 뒤로가거나 검색해서 아예다른 페이지로 가거나 등등의 동작들을 수학적 모델링을 하였다.

Random Walk

p_i^{t+1} = \sum_{j\in N(i)}\frac{p^t_j}{d_j^{out}} = \sum_j \frac{A_{ji}}{d_j^{out}} p_j

$p_i$ 에 $t+1$ 에 있을 확률은 $i$ 를 out-degree로 가리키는 노드 $j$ 들이 타임스탬프 $t$ 에 있을 확률의 합이다. 이때 각 노드들의 out-edge가 여러 개일 수도 있으므로 각각의 그 개수만큼 나누어 준다
이를 인접행렬 표현식을 통해 간단하게 표현할 수도 있다.

p^{t+1} = (D^{-1}A)^T p^t \ \ \ , \ \ D_{ii} = diag\{d_i^{out}\}

P = D^{-1}A \ \ \ , \ \ p^{t+1} \larr P^Tp^t

D행렬은 각 노드들의 out-degree를 담은 diagonal matrix이고 위 식에서 out-degree를 나누어주기 때문에 역행렬을 취한다.
P는 고정된 행렬이기에 최종적으로 요약하면 다음과 같이 나타낼 수 있을 것이다.
Random walk만 사용하였을 때의 단점은 out-degree가 0인 노드에서는 다른 페이지로 나갈 방법이 없다. 이는 Strongly하게 연결되어있지 않기에 결국 특정 노드에 고립되는 것이다. 이를 Strongly Connected Component로 만들어주기 위해서는 약간의 추가적인 edge를 만들어주면 되는데 이를 개념적으로 가능하게할 수 있다.

Teleportation

Power Iteration

p^{t+1} \larr \alpha P^Tp^t + (1-\alpha)\frac{e}{n}

일정확률( $\alpha$ )로 그래프의 특정 노드 중 무작위 하나로 순간이동하는 하나 추가하였다. 이를 통해 특정한 노드에 영원히 고립되는 것을 방지할 수 있다.
실제 $\alpha$ 값은 0.85 정도가 사용되고 즉 15% 확률로 무작위 다른 노드로 점프한다는 뜻이다.

Sparse Linear System

(I-\alpha P^T)p = (1-\alpha)\frac{e}{n}

다음과 같이 희소행렬의 선형방정식 형태로 나타낼 수도 있다.

Eigenvalue Problem $(\alpha P^T + (1-\alpha)E)p = \lambda p$

다음과 같이 eigenvalue 문제로 바꾸어 해결할 수 있다.

Markov Chains

조건
- stochastic : 각 확률은 음수가 아니어야하고 각 행의 확률의 합은 1이어야한다.
- 확률이 1을 넘어가면 마르코프체인에 의해 수렴하지 않고 발산할 수도 있음
  - ex) 노드 a가 b,c와 연결된다면 a,b a,c 각각 0.5가 된다
- irreducible : strongly connected graph가 되어 모든 정점을 갈 수 있음을 보장해야한다
  - ex) teleportation으로 가능함
- aperiodic : 주기가 있으면 특정 루프에 갇혀 수렴이 잘 안될 수도 있다.
  - page rank에서는 teleportation이 있기에 특정 루프에 갇히게 될 가능성이 낮다.
위의 조건을 만족하였을 때 일정시간이 지나면 아래와 같이 확률은 특정 값으로 수렴하게 된다.

\lim_{t\rarr \infin} p^{-t} = \bar{\pi}

즉 Random suffer를 무한히 반복한다면 이 값을 수렴할 것이고 이 수렴한 결과를 각 페이지의 가중치라고 생각할 수 있을 것이다.

HITS (Hubs and Authorities)

대규모의 그래프에는 잘 작동하지 않아 널리사용되지는 않지만 굉장히 아이디어가 좋은 알고리즘이다.
pagerank와 달리 총 2개의 점수가 있는데 Authorities는 말 그대로 권위를 나타내는 점수이고 hubs는 연결하는 커넥터 역할을 한다.
Authorities
- 좋은 허브에게 지목을 많이 당하면 권위성이 높다
  $a_i \larr \sum_j A_{ji}h_j$
Hubs
- 권위성이 높은 노드를 많이 지목하면 좋은 허브이다. $h_i \larr \sum_jA_{ij}a_j$
Linear equations $a = \alpha A^Th$ $h = \beta Aa$
Eigenvalue Problem
$(A^TA)a = \lambda a$
$(AA^T)h = \lambda h$
- 비대칭 행렬의 고유값은 음의 고유값 값을 가지게 하고 특정값에 수렴을 보장되지 않기 때문에 transpose와 연산을 통해서 대칭행렬로 만들어주어 고윳값을 구해야한다.

Eigenvalue in PageRank

pagerank와 HITS 모두 공통적으로 다루고있는 eigenvalue를 구하는 문제에 대해서 알아보자
eigenvalue는 선형변환을 하여도 방향이 바뀌지 않고 스칼라의 크기만 바뀌는 값이다.
여기서 가장 중요한 규칙은 우리는 개념적으로 선형변환을 연쇄적으로 계속하며 확률값이 변하지 않을 때까지 반복하는 것이고 그 확률값이 변하지 않도록 하는 축을 찾는 것을 목표로한다.
1. 초기의 p가 존재할 것이고 여기서 특정 P를 계속 곱하더라도 $p = \lambda p$ 로 안정적으로 수렴하도록하는 것을 목표로하고 $\lambda =1$ 일 때 최종적으로 수렴하게된다.
2. $\lambda = 1$ : 수학적으로 확률 행렬에는 람다가 1인 값이 무조건 존재하게되고 이 값이 해가 된다.
3. $\lambda \gt 1$ : 하지만 확률 행렬의 한 행의 확률의 합이 1을 넘지 않으니 람다가 1보다 큰 고윳값은 존재하지 않게된다.
4. $\lambda \lt 1$ : 람다가 1보다 작은 고윳값은 곱을 반복하면 결국 람다가 0에 수렴하며 모든 축이 람다가 1인 축으로 흡수되게 된다
5. 따라서 이 문제를 해결하기 위해 주어진 행렬에서 고윳값 분해를 하여 람다가 1(혹은 1에 가장 가까운 (수치적오차))인 값을 찾아서 그 고윳값에 대한 고유벡터를 구하면 그 값이 해가 된다.