[Network Science]6. Structural Properties of Networks Structural Equivalence
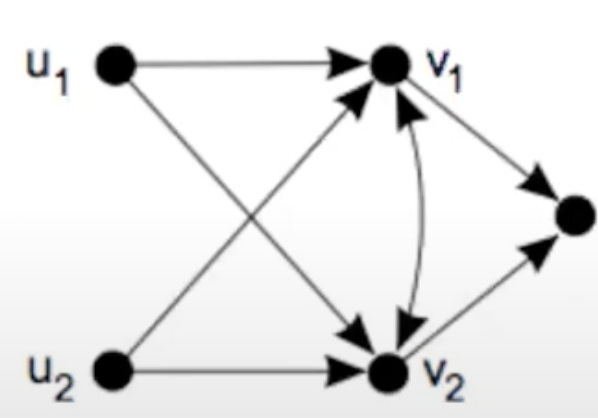
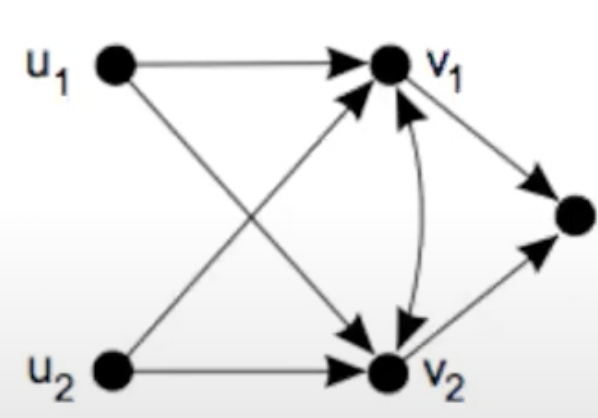
노드의 in-neighbors와 out-neighbors가 완전히 동일하다면 구조적으로 동일하다고 표현할 수 있다.
위 규칙에 따르면 v1과 v2와 같이 서로 연결된 노드 사이에는 다른 이웃이 동일하다고 하여도 동일성을 만족하지 못한다. 따라서 모든 노드에 self-loop를 추가하여 일관성을 부여할 수 있다.
하지만 엄격한 구조적 동등성의 경우 실제 상황에서는 굉장히 드물기 때문에 일반적으로 다른 지표를 사용한다.
Structural Similarity
구조적으로 동일한지 안한지의 이분법적 방식이 아닌 얼마나 유사한지를 측정하는 측정법이다.
진짜 구조만 보고 판단하기에 일반적으로 인접행렬을 이용하여 측정할 수 있고 기준에 따라 측정하는 지표는 아래와 같이 다양하다. 하지만 이 모두 Neighbor 정보를 이용하여 유사성을 측정한다라는 점에서 일맥상통한다.
Jaccard Similarity
J ( v i , v j ) = ∣ N ( v i ) ∩ N ( v j ) ∣ ∣ N ( v i ) ∪ N ( v j ) ∣ J(v_i,v_j) = \frac{|N(v_i)\cap N(v_j) |}{|N(v_i)\cup N(v_j) |} J ( v i , v j ) = ∣ N ( v i ) ∪ N ( v j ) ∣ ∣ N ( v i ) ∩ N ( v j ) ∣ Cosine Silmilarity
σ ( v i , v j ) = c o s ( θ i j ) = ∑ k A i k A j k ∑ A i k 2 ∑ A j k 2 \sigma(v_i,v_j) = cos(\theta_{ij}) = \frac{\sum_k {A_{ik}A_{jk}}}{\sqrt{\sum A^2_{ik}}\sqrt{\sum A^2_{jk}}} σ ( v i , v j ) = c o s ( θ i j ) = ∑ A i k 2 ∑ A j k 2 ∑ k A i k A j k Pearson Correlation Coefficient
r i j = ∑ k ( A i k − ⟨ A i ⟩ ) ( A j k − ⟨ A j ⟩ ) ( A i k − ⟨ A i ⟩ ) 2 ( A j k − ⟨ A j ⟩ ) 2 r_{ij} = \frac{\sum_k (A_{ik}-\langle A_i\rangle)(A_{jk}-\langle A_j\rangle)}{\sqrt{(A_{ik}-\langle A_i\rangle)^2} \sqrt{(A_{jk}-\langle A_j\rangle)^2}} r i j = ( A i k − ⟨ A i ⟩ ) 2 ( A j k − ⟨ A j ⟩ ) 2 ∑ k ( A i k − ⟨ A i ⟩ ) ( A j k − ⟨ A j ⟩ )
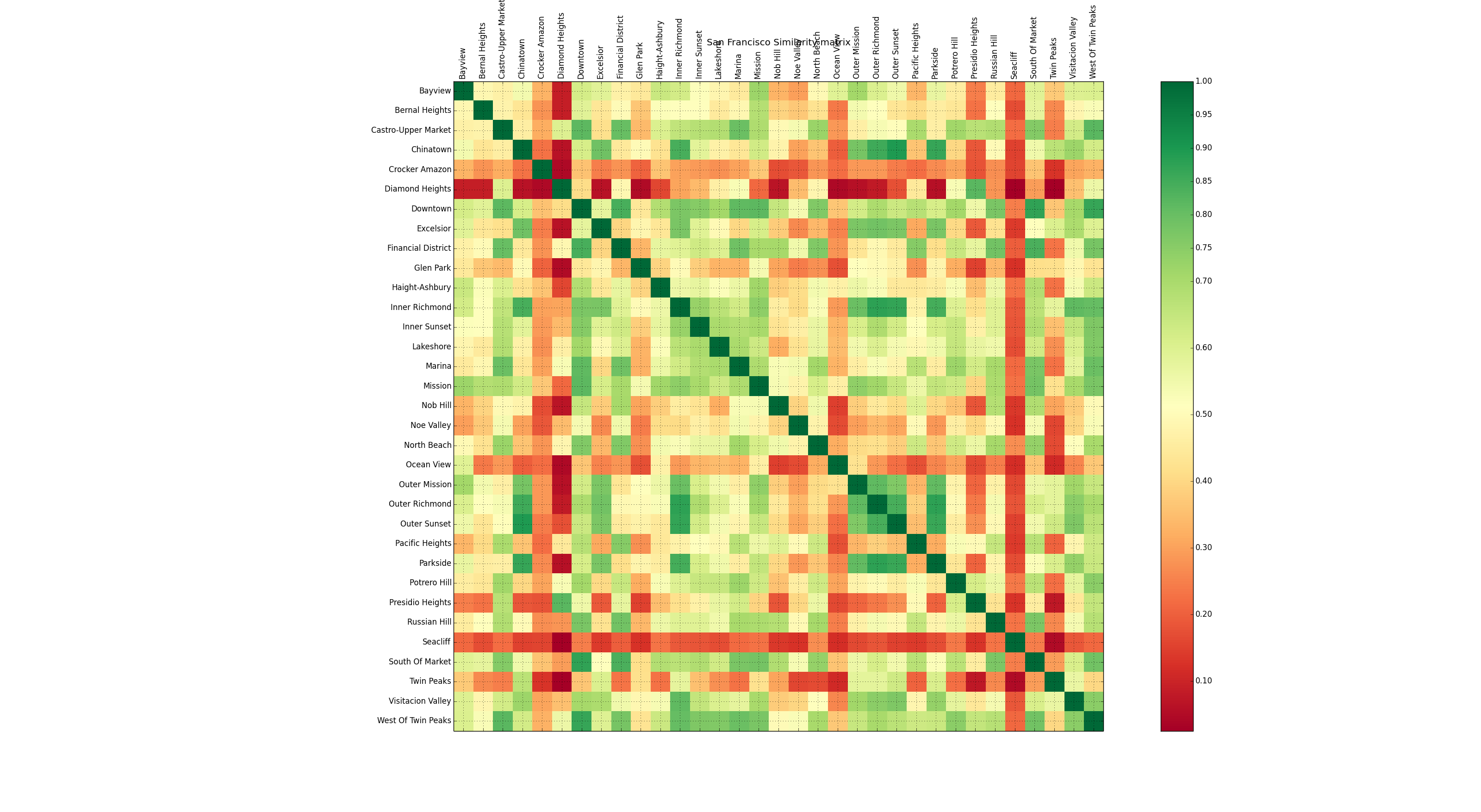
이를 통해 노드 간에 서로 얼마나 유사한지에 대한 Matrix도 얻을 수 있다.
SimRank
s ( a , b ) = C ∣ I ( a ) ∣ ∣ I ( b ) ∣ ∑ i = 1 I ( a ) ∑ j = 1 I ( b ) s ( I i ( a ) , I j ( b ) ) , a ≠ b s(a,b) = \frac{C}{|I(a)||I(b)|} \sum^{I(a)}_{i=1}\sum^{I(b)}_{j=1}s(I_i(a),I_j(b)), \ \ \ a \ne b s ( a , b ) = ∣ I ( a ) ∣ ∣ I ( b ) ∣ C i = 1 ∑ I ( a ) j = 1 ∑ I ( b ) s ( I i ( a ) , I j ( b ) ) , a = b s ( a , a ) = 1 s(a,a) = 1 s ( a , a ) = 1
PageRank 알고리즘처럼 두 노드의 유사성을 측정하기위해서 두 노드의 이웃의 유사성을 재귀적으로 사용한다. 이 때 초기에 같은노드는 유사성을 1로 두고 나머지는 모두 0으로 두게된다.
그 후 반복적인 업데이트를 통해 0이었던 유사도는 점점 늘어나게될 것이고 일정 시간 이후 수렴하는 것을 목표로 한다.
S i j = C k i k j ∑ k , m A k i A m j S k m S_{ij} = \frac{C}{k_ik_j}\sum_{k,m}A_{ki}A_{mj}S_{km} S i j = k i k j C k , m ∑ A k i A m j S k m Degree Correlation
r = c o v v a r = ∑ i j A i j ( k i − ⟨ k ⟩ ) ( k j − ⟨ k ⟩ ) ∑ i j A i j ( k i − ⟨ k ⟩ ) 2 r = \frac{cov}{var} = \frac{\sum_{ij}A_{ij}(k_i-\langle k \rangle)(k_j - \langle k \rangle)}{\sum_{ij}A_{ij}(k_i- \langle k \rangle)^2} r = v a r c o v = ∑ i j A i j ( k i − ⟨ k ⟩ ) 2 ∑ i j A i j ( k i − ⟨ k ⟩ ) ( k j − ⟨ k ⟩ )
서로 인접한 노드 간의 상관계수를 구하여 그래프 전체의 상관계수를 구한다.
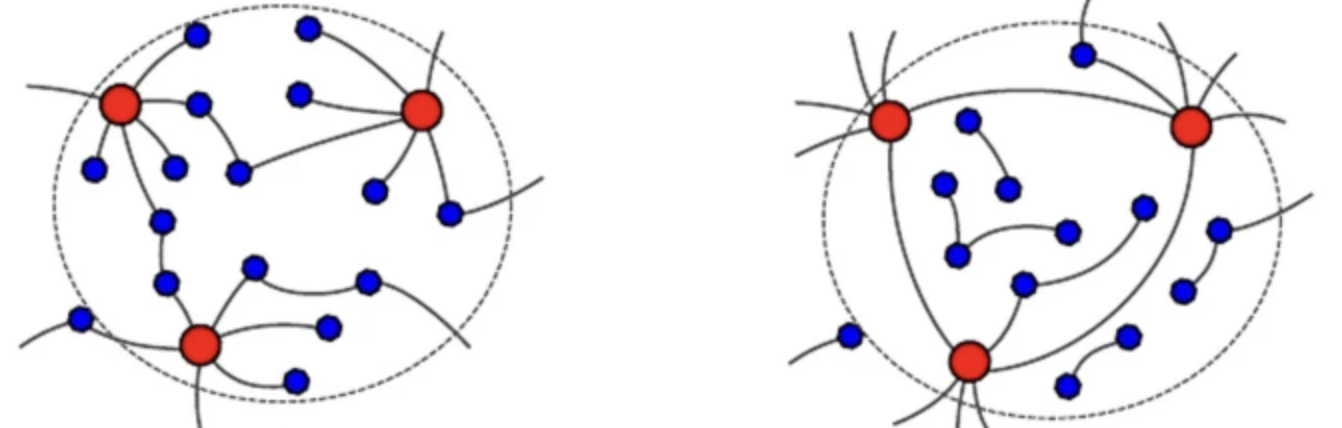
degree가 높은 노드가 높은 노드와 연결될 수록 r은 1로 커지고 높은 노드와 낮은 노드가 연결될 수록 r은 -1로 작아진다. 이를 통해 전체 그래프가 degree에 대해 동질성을 가지는지 이질성을 가지는지에 대한 평가지표로 사용가능하다.
왼쪽처럼 서로 다른 degree와 연결된 경우 r은 작아지고 오른쪽처럼 서로 비슷한 degree의 노드와 연결된 경우 r은 커지게 된다.
e k , k ′ = m ( k , k ′ ) m e_{k,k^\prime} = \frac{m(k,k^\prime)}{m} e k , k ′ = m m ( k , k ′ )
degree가 k k k k ′ k^\prime k ′
k n n ( k ) = ∑ k ′ k ′ P ( k ′ ∣ k ) P ( k ′ ∣ k ) = e k , k ′ ∑ k ′ e k , k ′ k_{nn}(k) = \sum_{k\prime} k^\prime P(k^\prime|k) \ \ \ \ P(k^\prime|k) = \frac{e_{k,k^\prime}}{\sum_{k^\prime}e_{k,k^\prime}} k n n ( k ) = k ′ ∑ k ′ P ( k ′ ∣ k ) P ( k ′ ∣ k ) = ∑ k ′ e k , k ′ e k , k ′
노드의 degree가 k일 때 neighbor의 degree의 평균을 구하는 공식이다.
조건부확률로 degree가 k인 노드 이웃 중 k ′ k^\prime k ′ k ′ k^\prime k ′
Assortative
위에서 보았듯이 비슷한 유형(차수)의 노드가 서로 연결되는 형태를 Assortative라고 하고 서로 다른 유형의 노드가 연결되는 형태를 Disassortative라고 한다. 이러한 개념을 차수가 아닌 즉 구조적인 관점에서 내용적인 관점으로 전환할 수 있다.
그 노드가 가지고있는 attribute(성별, 연령대 등)에 따라 노드가 서로 비슷하거나 반대되는 것에 연결되는 경향성을 확인할 수 있다.
Assortative mixing
이러한 특성을 측정하기위해 mixing을 사용한다. 얼마나 비슷한 것끼리 연결되어있는지 측정할 수 있다.
Q = m c − ⟨ m c ⟩ m Q = \frac{m_c - \langle m_c \rangle}{m} Q = m m c − ⟨ m c ⟩
전체 그래프에서 같은 클래스끼리 연결된것의 비율을 구한다. 이 때 랜덤그래프에서의 해당 노드들이 연결되는 비율을 빼줌으로써 랜덤할 때의 기대값보다 얼마나 큰지에 대한 측정을 가능하게 한다.
이 식은 Modularity라고 말하며 다시말해 그래프가 같은 집단끼리 얼마나 잘 분류되었는지에 대한 지표이기도 하다.
Q = 1 2 m ∑ i j ( A i j − k i k j 2 m ) δ ( c i , c j ) Q = \frac{1}{2m}\sum_{ij}\left( A_{ij}-\frac{k_ik_j}{2m}\right)\delta(c_i,c_j) Q = 2 m 1 i j ∑ ( A i j − 2 m k i k j ) δ ( c i , c j )
계산식으로 나타내면 다음과 같고 δ ( c i , c j ) \delta(c_i,c_j) δ ( c i , c j )
즉 같은 클래스일 때만 계산을 하게 되는데 이 때 A i j A_{ij} A i j
Q Q m a x = ∑ i j ( A i j − k i k j 2 m ) δ ( c i , c j ) 2 m − ∑ i j k i k j 2 m δ ( c i , c j ) \frac{Q}{Q_{max}} = \frac{\sum_{ij}\left( A_{ij}-\frac{k_ik_j}{2m}\right)\delta(c_i,c_j)}{2m - \sum_{ij}\frac{k_ik_j}{2m}\delta(c_i,c_j)} Q m a x Q = 2 m − ∑ i j 2 m k i k j δ ( c i , c j ) ∑ i j ( A i j − 2 m k i k j ) δ ( c i , c j )
최대로 가능할 때의 Q m a x Q_{max} Q m a x
이는 같은 클래스 인지 아닌지에 대한 범주형 속성일 때 적용가능한 수식이다
r = c o v v a r = ∑ i j A i j ( x i − ⟨ x ⟩ ) ( x j − ⟨ x ⟩ ) ∑ i j A i j ( x i − ⟨ x ⟩ ) 2 = ∑ i j ( A i j − k i k j 2 m ) x i x j ∑ i j ( k i δ i j − k i k j 2 m ) x i x j r = \frac{cov}{var} = \frac{\sum_{ij}A_{ij}(x_i-\langle x \rangle)(x_j-\langle x \rangle)}{\sum_{ij}A_{ij}(x_i-\langle x \rangle)^2} = \frac{\sum_{ij}\left( A_{ij}-\frac{k_ik_j}{2m}\right)x_ix_j}{\sum_{ij}\left( k_i \delta_{ij}-\frac{k_ik_j}{2m}\right) x_ix_j} r = v a r c o v = ∑ i j A i j ( x i − ⟨ x ⟩ ) 2 ∑ i j A i j ( x i − ⟨ x ⟩ ) ( x j − ⟨ x ⟩ ) = ∑ i j ( k i δ i j − 2 m k i k j ) x i x j ∑ i j ( A i j − 2 m k i k j ) x i x j
범주가 아닌 스칼라 값을 다루는 경우 위와 같이 degree coefficient를 다루는 것 처럼 다룰 수 있다.
r = c o v v a r = ∑ i j ( A i j − k i k j 2 m ) k i k j ∑ i j ( k i δ i j − k i k j 2 m ) k i k j r = \frac{cov}{var} = \frac{\sum_{ij}\left( A_{ij}-\frac{k_ik_j}{2m}\right)k_ik_j}{\sum_{ij}\left( k_i \delta_{ij}-\frac{k_ik_j}{2m}\right) k_ik_j} r = v a r c o v = ∑ i j ( k i δ i j − 2 m k i k j ) k i k j ∑ i j ( A i j − 2 m k i k j ) k i k j
추가적으로 위 수식에서 x를 degree로 바꾸어 수식을 다시 전개하면 다음과 같이 바꿀 수 있고
r = S e S 1 − S 2 2 S 3 S 1 − S 2 2 r = \frac{S_eS_1 - S_2^2}{S_3S_1-S^2_2} r = S 3 S 1 − S 2 2 S e S 1 − S 2 2 S 1 = ∑ i k i = 2 m , S 2 = ∑ i k i 2 , S 3 = ∑ i k i 3 , S e = ∑ i j A i j k i k j S_1 = \sum_i k_i = 2m , \ S_2 = \sum_ik^2_i , \ S_3 = \sum_i k_i^3 , \ S_e = \sum_{ij}A_{ij}k_ik_j S 1 = i ∑ k i = 2 m , S 2 = i ∑ k i 2 , S 3 = i ∑ k i 3 , S e = i j ∑ A i j k i k j
위와같은 형태로 수정하여 degree coefficient를 간단하게 구할 수 있다.
Properties of Degree Assortative Graph
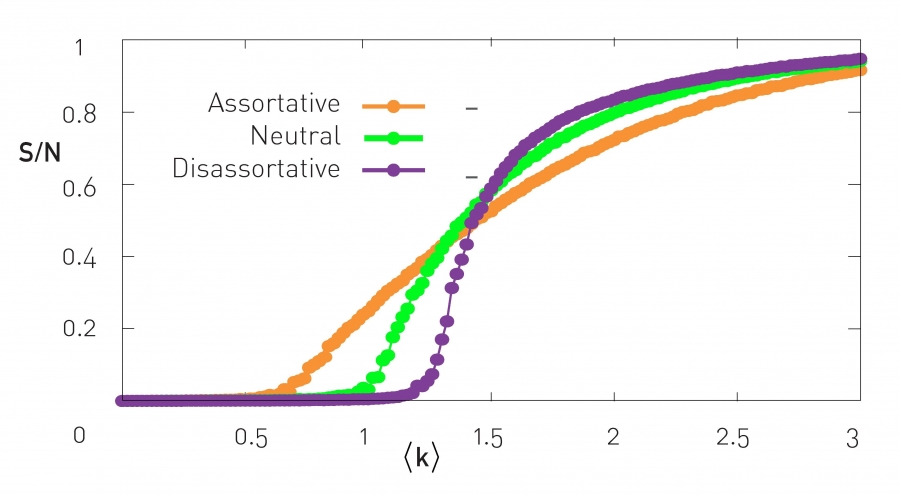
이를 이용하여 그래프의 특성을 파악할 수 있는데 Assortative한 그래프인 경우 Phase Transition이 발생하는 시기가 빠르다. 이는 degree가 큰 노드끼리 빠르게 뭉치는 경향이 있기 때문이다.
하지만 임계치 이후의 증가속도는 Disassortative한 그래프가 더 큰데 이유는 Phase Transition이 발생하기전까지 모아놓았다가 시간이 지나면 연쇄적으로 연결되기에 훨씬 빠르게 연결되는 경향이 있다.
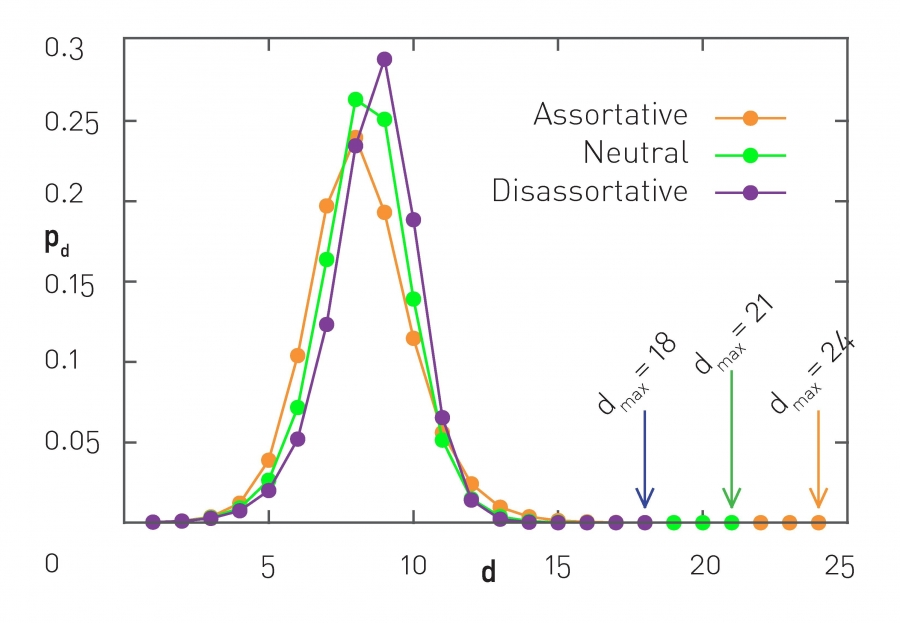
또 다른 특성은 Path Length의 분포이다. Assortative한 그래프는 상대적으로 짧은 path의 길이가 많지만 차수가 낮은 노드는 낮은 노드끼리 연결이 되기에 그 연결이 굉장히 길어지는 구간이 발생할 수 있다. 따라서 결과적으로 diameter는 커지게 된다.
Friendship paradox
“Your friends are more popular than you are”
k n n ( k ) = ∑ k ′ k ′ P ( k ′ ∣ k ) k_{nn}(k) = \sum_{k\prime} k^\prime P(k^\prime|k) k n n ( k ) = k ′ ∑ k ′ P ( k ′ ∣ k )
이전에 우리는 다음과 같은 degree분포를 볼 수 있었고 이것이 correlation이 없는 random graph라고 가정하고 이 paradox를 다루어보면 조건부확률 대신 randomly하게 연결되는 것을 가정할 수 있다.
P ( k ′ ∣ k ) → k ′ P ( k ′ ) ⟨ k ⟩ P(k^\prime|k) \ \ \rarr \ \ \frac{k^\prime P(k^\prime)}{\langle k \rangle} P ( k ′ ∣ k ) → ⟨ k ⟩ k ′ P ( k ′ )
확률은 단순히 k ′ k^\prime k ′
k n n = ∑ k ′ k ′ k ′ p ( k ′ ) ⟨ k ⟩ = ⟨ k 2 ⟩ ⟨ k ⟩ k_{nn} = \sum_{k^\prime}k^\prime\frac{k^\prime p(k^\prime)}{\langle k \rangle} = \frac{\langle k^2 \rangle}{\langle k \rangle} k n n = k ′ ∑ k ′ ⟨ k ⟩ k ′ p ( k ′ ) = ⟨ k ⟩ ⟨ k 2 ⟩
따라서 정리하면 최종적으로 위와 같이 정리할 수 있을 것이다.
Random Network에서 ⟨ k 2 ⟩ = ⟨ k ⟩ ( 1 + ⟨ k ⟩ ) \langle k^2 \rangle = \langle k \rangle(1+\langle k \rangle) ⟨ k 2 ⟩ = ⟨ k ⟩ ( 1 + ⟨ k ⟩ ) k n n = 1 + ⟨ k ⟩ k_{nn} = 1 + \langle k \rangle k n n = 1 + ⟨ k ⟩
만약 scale-free network의 경우에는 ⟨ k 2 ⟩ \lang k^2 \rang ⟨ k 2 ⟩
쉽게 말해 일반적으로 우리가 차수가 굉장히 높은 사람을 한두 명만 만나더라도 그 사람에 의해 내 친구의 평균 수가 엄청나게 올라가게 될 것이다. 이를 통해 역설이 설명가능하다.