Graph Partioning
- 하나의 graph를 여러 개의 작은 subgraph로 분할하는 방법
- 그래프를 분할하는 방법은 총 을 따르기 때문에 NP-hard문제가 될 것이고 정확한 답이 아닌 최적화를 통해 최적인 값을 찾는 휴리스틱 알고리즘을 사용해야한다.
- 가장 기본적인 방식은 Cut을 이용하는 것이다. 즉 서로 다른 집단을 구분할 때 그 집단 사이의 edge를 제거한다고 한다면 제거되는 edge가 최소가 될 수록 서로 동일한 집단에 있다라고 기대할 수 있을 것이다.
Cut
-
Graph cut
- 이 방식은 굉장히 취약점이 많다. Q를 최소화하는 것을 목표로하기에 최솟값은 1이 될 것이고
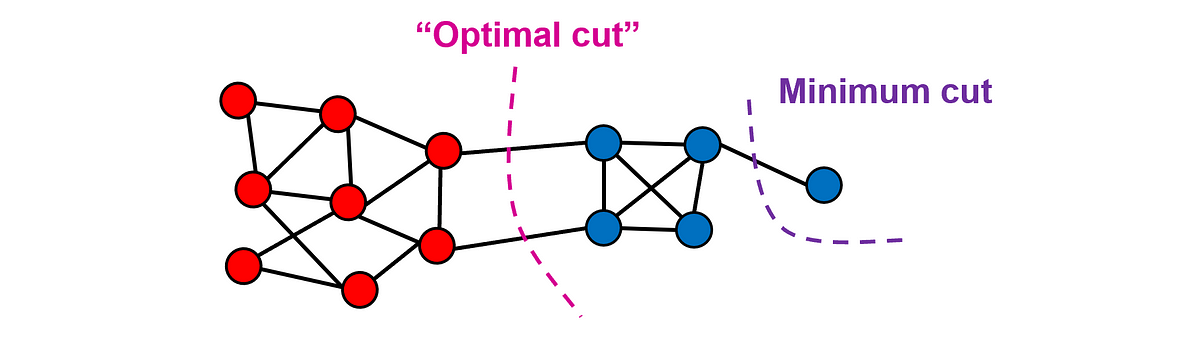
- 위와 같은 상황에서 최적이아니지만 minimum cut을 선택할 것이다. 따라서 일반적으로 이것을 직접적으로 사용하지는 않고 이것을 이용한 다른 방법들을 사용한다
- 이 방식은 굉장히 취약점이 많다. Q를 최소화하는 것을 목표로하기에 최솟값은 1이 될 것이고
-
Ratio cut
- 각 집단에 노드의 개수가 적절하게 분배되도록 가중치를 부여한 방식. 이를 통해 위와 같은 문제를 개선하여 극단적인 최적화를 방지할 수 있음
-
Normalized cut
- Ratio cut보다 일반적으로 더 잘 작동한다. 그 이유는 Ratio cut은 집단 내의 노드의 개수만 고려하기 때문에 그 노드 간의 연결이 다소 약하더라도 하나의 집단으로 묶어버릴 수도 있다
- Normalized cut은 이러한 경우를 막기위해 추가적으로 각 집단 내의 연결성도 반영한 최적화 방식이라고 볼 수 있다.
- 또한 edge의 neighbor를 이용하기 때문에 adjacency matrix로 표현하기에도 매우 좋다
-
Quotient cut
- 굉장히 좋은 방식이지만 실제로는 잘 사용되지는 않음. min을 사용하기 때문에 미분이 불가능함
Karger’s Algorithm
- 이 방식은 가장 기본적인 Graph cut을 최적화 함수로 사용하는 방식이다.
Edge Contraction
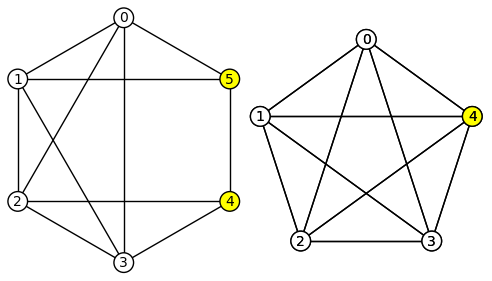
- Edge Contraction은 서로 다른 두 노드 사이의 edge를 자르며 두 노드를 하나로 합치는 것이다.
- 물론 이 때 두 노드의 neighbor들도 하나로 합치게된다. 1개로 만든다는 뜻이 아니고 서로 다른 노드 A,B가 1개의 이웃 C를 모두 가리키고 있다면 합쳐진 노드는 노드 C에 대해 2개의 edge를 가지고 있을 것이다.
Algorithm
- N개의 노드를 가지는 Graph가 주어진다
- Edge Contraction을 N-2번 반복하면 최종적으로는 2개의 Node와 그 사이에 연결된 여러 개의 edge가 존재할 것이다.
- 이 때 그 사이에 연결된 edge가 서로 다른 두 집합 사이의 연결 혹은 라고 생각할 수 있다.

- 하지만 이 알고리즘을 실행시키고 나서 얻은 값이 최소의 값을 가질 확률은 이다. 즉 굉장히 낮다고 말할 수 있고 따라서 우리는 이 알고리즘을 여러 번 반복시켜 얻은 결과 중 가장 작은 결과를 채택하면 최소의 값을 가질 확률은 올라가게 될 것이다.
Time Complexity
- 가장 먼저 Karger’s Algorithm은 한번 실행시키는데 을 필요로한다.
- k번 반복했을 때 실패확률이 굉장히 작아지려면 얼마나 반복해야하나
- 다음과 같이 증명가능하고 즉 번 실행한다면 거의 항상 최적의 값을 찾을 수 있다.
- 전체적인 시간복잡도는 이 되게 된다.
Linear algebra of graph cut
- 이전에는 graph cut을 단순히 시각적인 개수의 형태로 바라보았다면 여기서는 선형대수의 측면에서 바라볼 수 있다.
- 각각의 와 로 그룹이 나누어졌다고 가정하였을 때 이런식으로 각 node에 대한 벡터를 표현할 수 있을 것이다
- 이를 이용하여 를 구해보면
-
처음을 보면 는 잘라야할 edge의 개수이다. 서로 다른 집합끼리 연결된 edge는 1의 값을 서로 같은 집합의 edge는 0의 값을 가져야할 것이고 이를 위한 수식이 다음에 오는 이다.
-
여기서는 edge의 집합을 사용하였지만 확장하여 adjacency matrix를 사용하면 다음과 같이 나타낼 수 있고 edge가 상호 연결되어있기에 1/2을 더 곱해주고 1/8로 사용한다.
-
이를 전개하고 크로네커 델타 표기법을 사용하여 조금 수정하면
여기까지 올 수 있다. -
이를 차수 행렬로 표현하면 로 유도가능하다.
-
다음의 형태를 최종적으로 라플라시안 행렬의 형태로 나타내어 사용할 수 있다.
Laplacian matrix
- 라플라시안 행렬에 대해 잠깐 보고 가자면
- 구성
- 대각 성분은 각 노드의 degree가 된다
- 인접한 노드가 있는 곳에는 -1이 된다.
- 나머지는 0으로 채워진다.
- 특징
- symmetric한 구조를 가지고있다.
- 각 row, column의 합은 0이 된다.
- 그래프를 다룰 때 유용하게 사용되는 matrix이다.
Spetral method
- 위에서 우리는 최종적으로 다음과 같은 식을 유도할 수 있었다.
- 이 식을 가장 작게 만드는 즉 최적화를 하여 cut을 진행할 수 있다.
- 추가적으로 각 그룹간의 균형있는 결과를 위해 의 규제항을 추가하여 각 그룹의 노드의 개수가 어느 정도 일정하도록 조정한다. 완전히 균형이 맞을 때, 각 그룹의 노드의 개수가 맞을 때 다음 항은 0이 될 것이다.
- 하지만 잘 생각해보면 우리가 가지고 있는 값들은 Q(s), 그리고 규제항 모두 정수 값 들이다. 즉, 우리가 아는 것처럼 최적화하는 방법은 쉽지 않고 시뮬레이션을 돌려보아야 하는데 그것은 NP-hard이기 때문에 다른 조치가 필요하다.
- 따라서 우리는 로 바꾸어 최적화 문제를 풀 것이고 실수값의 답이 나온다면 최종적으로 를 이용해 정수값으로 변환하여 출력할 것이다.
- 이때 이라는 제약조건이 하나 더 추가된다.
라그랑주 승수법
- 이 제약 조건을 추가하여 라그랑주 승수법을 사용할 수 있다.
Eigenvalue
- 미분하면 다음과 같은 형태로 나오게되고 이는 L이 주어졌을 때의 eigenvalue 문제의 형태와 같다
- 이때 eigenvector 와 eigenvalue 를 찾아 대입하면 다음과 같이 정리된다.
Solution
- 이때 라플라시안 행렬의 특징 중 하나는 가장 작은 eigenvalue의 값은 이고 이 때 eigenvector는 라는 것이 자명하다는 것이다. 그 이유는 이전에 보았듯이 라플라시안 행렬의 행의 합이 1이되는 것 때문이다.
- 따라서 가장 작은 eigenvector의 값은 의 값을 만족시키지 못하기에 우리는 이 문제를 풀기 위해 두번째로 작은 eigenvalue에 해당하는 eigenvector를 이용할 것이다.
- 따라서 이 식을 풀게되면 라는 eigenvector가 나오게 될 것이고 실제로는
다음과 같이 변형하여 출력한다. - 추가적으로 를 통해 정규화하여 사용할 수 있다.
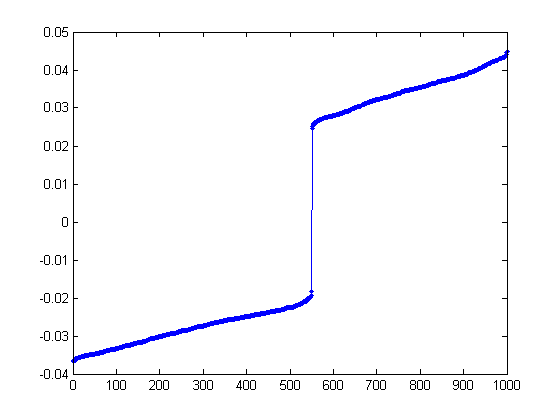
- 이렇게 구해진 x의 값들을 정렬해보면 다음과 같은 모습을 볼 수 있고 0을 기준으로 두개의 그룹으로 분할할 수 있다는 것을 볼 수 있다.
Recursive Partitioning
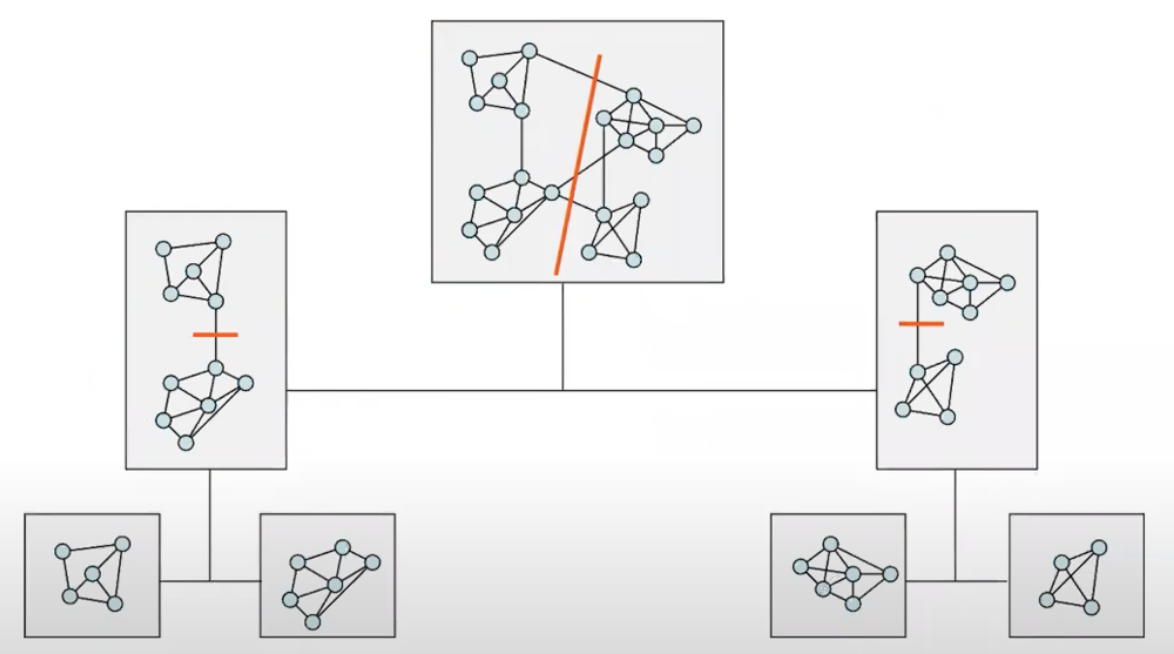
- 다음과 같이 재귀적으로 2그룹씩 그래프를 분할하며 밀도가 굉장히 높아질 때까지 반복하는 방법을 사용하여 여러 그룹으로 나눌 수 있다.
Multilevel Spectral
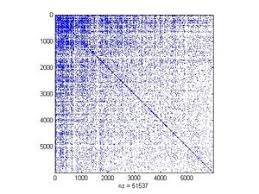
- 맨 처음 다음과 같이 adjacency matrix가 주어졌다고 가정하고 이를 Spectral Method를 사용한 후 eigenvector에 대해 정렬해본다면
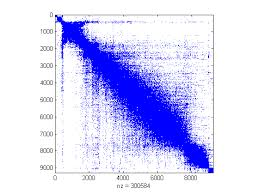
- 위와 같이 조금 군집이 보일 것이다. 만약 오른쪽 아래처럼 군집이 안보이는 곳이 있다면 해당 구역에 대해서만 또 Spectral Method를 적용한다면

- 최종적으로 다음과 같이 여러 군집을 발견할 수 있을 것이다. 이처럼 Spectral Method를 여러 번 사용하고 시각화를 통해 군집을 찾아내는 방법은 대규모 그래프에서 굉장히 유용한 방법이다.
