[Network Science]8. Community Detection

YongUk·2025년 2월 9일

GNN Graph network science

Graph Theory

목록 보기

10/17

Community Detection

같은 그룹끼리는 edge가 많이 연결되어야하고 상대적으로 다른 그룹끼리는 edge가 적게 연결되어야한다.
조금 더 정확하게 graph의 평균 edge보다 그룹내에는 더 많은 edge가 존재해야하고 서로 다른 그룹끼리는 edge가 적게 존재해야한다.

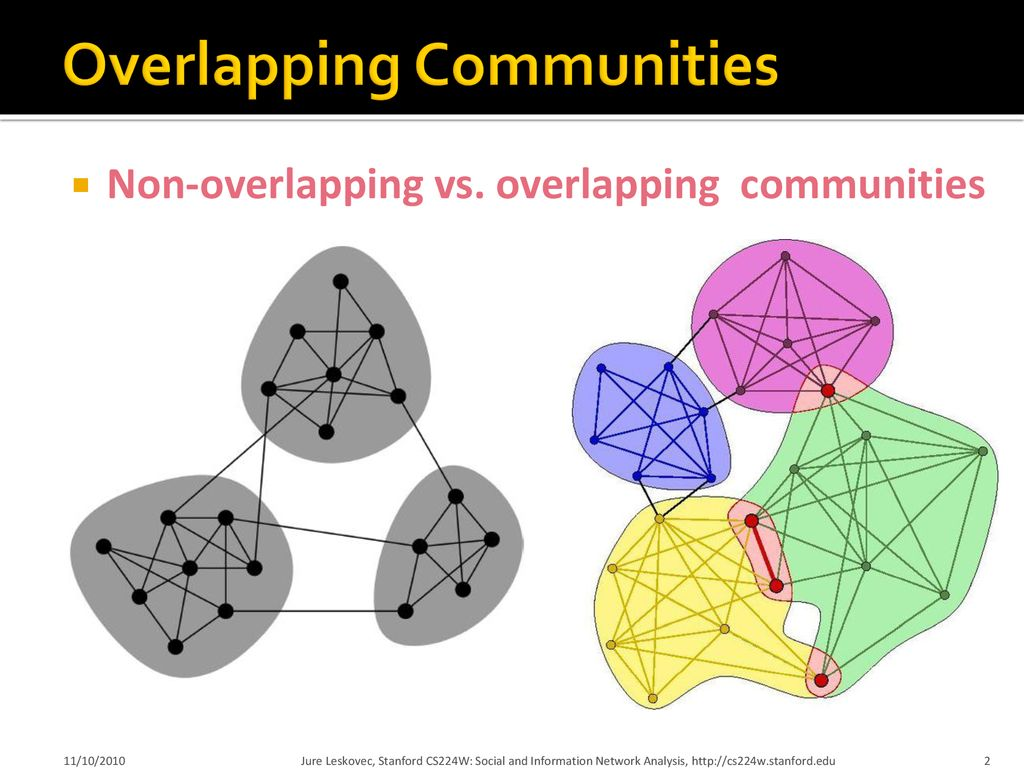
Overlapping & Non-overlapping community

하나의 노드가 여러개의 community에 속할 수 있는 경우에는 overlapping community라고 하고 노드가 한 개의 community에만 존재하는 경우에 non-overlapping community라고 말할 수 있다.

density

\rho = \frac{m}{n(n-1)/2}

그래프의 밀도 혹은 평균 연결 정도를 계산할 수 있다.

\delta_{int} = \frac{m_s}{n_s(n_s-1)/2} \ \ \ \ \ , \ \ \ \ \ \delta_{ext} = \frac{m_{est}}{n_s(n-n_s)}

그래프의 내부의 연결 강도와 외부와의 연결강도를 계산할 수 있는데 내부 강도는 일반적으로 그래프의 밀도보다는 높아야하고 외부 강도는 그래프의 밀도보다 낮아야한다.

modularity

density는 community를 탐지하기에는 좋은 지표가 아니다. 따라서 더 성능 좋고 대중적인 modularity를 사용할 수 있다.
modularity는 현재 그래프와 random graph를 비교하는 것으로 random graph에는 community가 없다고 가정을 하고 그것에 비해 얼마나 잘 community가 이루어졌는지에 대해 계산한다.

Q =\frac{1}{2m}\sum_{ij}\left(A_{ij}-\frac{k_ik_j}{2m}\right)\delta(c_i,c_j)

이전에 위와 같은 modularity 공식을 한번 보았다. 여기서는 편의성을 위해 위 식을 조금 수정하여 사용할 것이다.

Q = \sum_u\left(\frac{m_u}{m}-\left(\frac{k_u}{2m}\right)^2\right)

조금 보정한 식이고 위 식은 특이하게 community 개수가 1개 일 때는 0의 값을 가지게 된다. 또한 위 식은 -1/2에서 1의 값을 가질 수 있고 커짐에 따라 상대적으로 community detection이 잘 이루어졌다고 판단할 수 있다. 조금 이상하게 보이지만 일반적으로 잘 작동한다.

Graph Partitioning

graph partitioning을 통해 community detection을 수행할 수 있는데 먼저 둘의 차이를 먼저 보자
- Graph partitioning : 그래프를 최소한의 edge를 제거하여 여러 개의 subgraph로 만듬
- Community Detection : 그래프를 비슷한 특성이 있는 집단끼리 나눔
즉 Graph partitioning은 구조적인 연결을 중시한다면 community detection은 이보다는 조금 더 집단 간의 연결성을 중시한다고 표현할 수 있다.
이러한 Graph partitioning을 community detection에 사용할 수 있는데 multilevel partitioning을 통해 그래프를 계속해서 분할해 나가며 modularity가 가장 높았던 분할 지점을 선택하여 community를 찾아낼 수 있을 것이다.

Heuristic Approach

Graph Partitioning과 같이 정확한 community를 찾아내기 위해서는 NP-hard 문제가 될 것이고 대규모의 그래프에서는 실제로 정확한 값을 찾는 것은 불가능하다. 따라서 여기서 또한 최적의 값을 찾는것을 목표로하고 여기서 최적이란 일반적으로 modularity가 높은 것을 말한다.

Edge Betweenness

이전에 나온 노드 중심성 중 하나인 Betweenness Centrality의 개념을 사용한다

C_B(e) = \sum_{s \ne t} \frac{\sigma_{st}(e)}{\sigma_{st}}

서로 다른 노드의 최단거리에 현재 edge가 얼마나 많이 놓여있는지를 구하는 것이다.
이 중심성 지표를 이용하여 지표가 큰 edge를 순차적으로 제거해 나가는 방식이다. betweenness centrality가 높다라는 것은 서로 다른 community들의 징검다리 역할을 한다라는 것에서 나오는 아이디어이다.
알고리즘
1. $C_B(e)$ 를 모든 edge에 대해 구한다
2. 가장 중심성이 높은 edge를 제거한다
3. 위 2개의 단계를 반복한다.
4. modularity가 가장 높았던 시간의 값을 선택할 수 있다.
매 step마다 Betweenness Centrality를 계산해야하기 때문에 비용이 크다는 것이 큰 단점이다. 따라서 큰 네트워크에서 적용시키에는 무리가 있다.

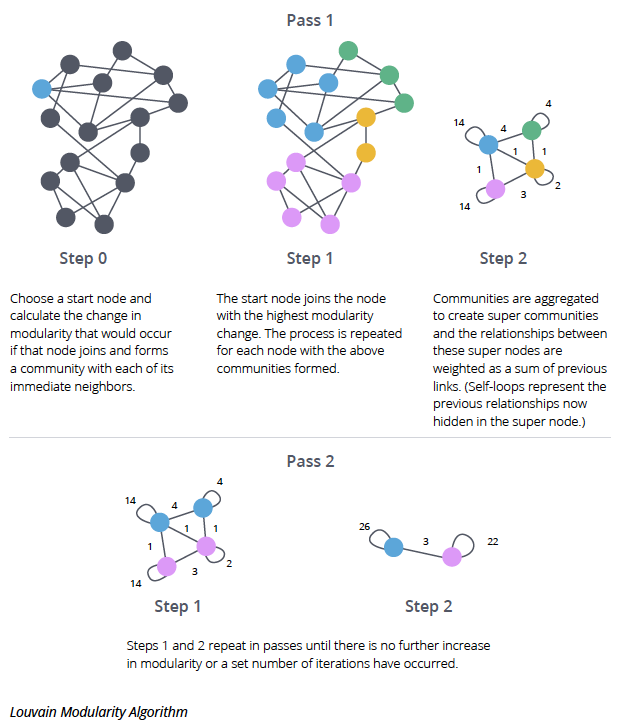
Louvain Algorithm

일종의 그리디 알고리즘으로 community detection을 수행한다.
또한 위 알고리즘의 단점을 보완하여 큰 그래프에서도 잘 작동하는 알고리즘이다.
알고리즘
1. 모든 노드는 자신의 커뮤니티를 가지고 시작한다. 즉 N개의 노드가 있다면 N개의 커뮤니티로 시작하는 것이다.
2. 모든 노드들은 각 스텝마다 이웃한 다른 커뮤니티에 흡수될지 되지않을지를 결정한다. 이때 기준은 modularity이고 이웃에 흡수되었을 때 modularity가 커진다면 흡수가 되고 그렇지 않다면 흡수되지 않는다. 또한 modularity가 커지는 이웃이 여러 개라면 최대인 경우를 선택한다. 이것이 그리디 알고리즘인 이유이다.
3. 한 노드가 다른 노드에 흡수되면 하나의 super node를 생성하고 해당 노드들 사이에 있던 edge들은 self-loop로 들어가게된다.
4. 위 과정을 modularity가 증가하지 않을 때까지 반복한다.

Hierarchical Clustering

개체들을 유사한 그룹으로 묶으며 계층적 트리 구조를 형성하는 기법이다.

Ravasz Algorithm

알고리즘
1. Similarity Matrix를 정의한다
  
  $x_{ij} = \frac{J(i,j)}{min(k_i,k_j)+1-\theta(A_{ij})}$
  - Ravasz 알고리즘에서는 다음과 같이 정의하였다.
  - $J(i,j)$ : 서로 공유하는 neighbor의 수
  - $\theta(A_{ij})$ : 서로 직접 연결되어있으면 1 아니면 0 (분모 보정용)
2. 각각의 노드들을 가장 유사한 노드들과 community로 묶는다. 이후에는 community들끼리의 유사도를 판단하여 비슷한 community끼리 묶는다.
  - 이 때 community의 유사도는 community 내부의 노드들의 유사도의 평균을 사용한다
  - 다른 방법도 있지만 ravasz algorithm에서는 평균을 사용한다
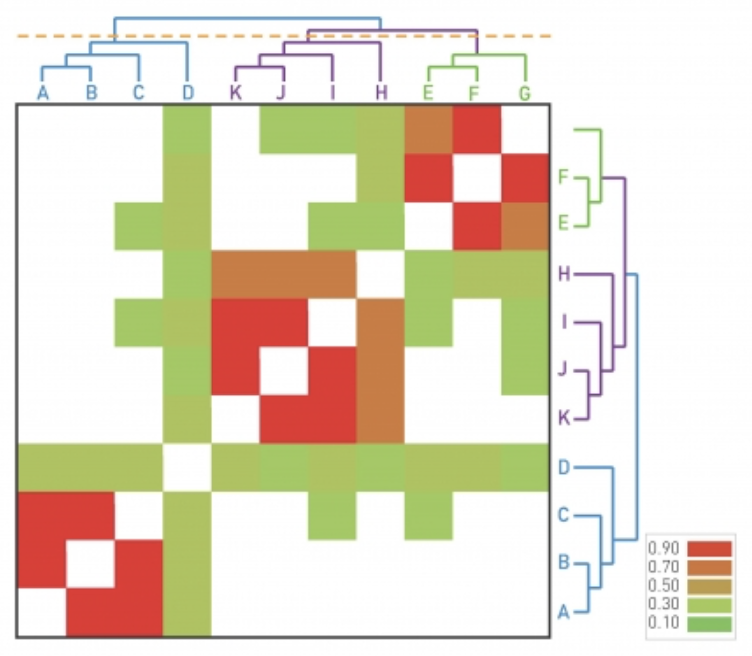
3. 이렇게 나온 결과를 다음과 같이 덴드로그램으로 표현한 후 modularity를 통해 적절한 분할지점을 찾는다.
하지만 모든 노드간의 유사도를 구하는 과정에서 비용이 많이 들기 때문에 대규모의 그래프에는 적합하지 않다.

Random Walk

임의 보행 기법을 기반으로 하며 무작위로 걸었을때 같은 군집 안을 많이 걸어다닐 것이라는 추측을 기반으로 하는 기법이다.
어떤 특정 노드에서 시작하여 Random walk를 하였을 때 주로 거쳐가는 노드들을 하나의 community로 묶을 수 있다.

Walktrap community detection

P = D^{-1}A

pagerank알고리즘과 동일하게 다음과 같은 공식을 사용할 수 있고 이 때 $P^t_{ij}$ 가 높다면 같은 community에 속한다고 말할 수 있다.
i,j가 같은 community에 존재한다면 k에 도달할 확률이 비슷할 것이다라는 것을 전제로하며 $P^t_{ik}$ 와 $P^t_{jk}$ 가 비슷하다면 i,j를 하나의 community로 병합한다.
이 때 둘의 비슷한 정도는 다음과 같이 쉽게 계산할 수 있다.

r_{ij}(t) = \sqrt{\sum_{k=1}^n \frac{P^t_{ik}-P^t_{jk})^2}{d(k)}} = \|D^{-1/2}P^t_i-D^{-1/2}P^t_j\|

이렇게 노드간의 거리를 구한 후 가까운 노드끼리 계층적으로 합하여 덴드로그램을 형성할 수 있다.

Walktrap Simluation

위의 식을 이용하여 행렬곱셈을 할 경우 복잡도가 크기 때문에 적절한 시뮬레이션을 통해서 구할 수도 있다.
k번의 simulation을 통해 i노드에서 k노드에 도달한 횟수 $N_{ik}$ 를 구하고 이를 $k$ 로 나누면 평균 도달 거리로 근사할 것을 될 것을 기대한다. $P^t_{ik} \approx \frac{N_{ik}}{K}$

Overlapping Community detection

이전까지 본 방식은 모두 겹치지 않는 Non-overlapping Community에서 적용가능한 알고리즘들이었다. 하지만 이 방식을 Overlapping Community에도 적용할 수는 없다.

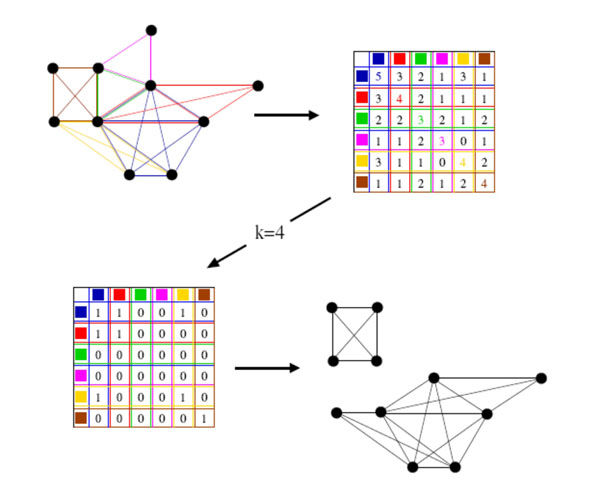
k-clique algorithm

알고리즘
1. 그래프에서 모든 clique를 찾는다.
2. 우리가 설정한 k에 따라 각각의 clique들이 k-1개의 노드를 공유하면 인접한것으로 아니면 인접하지 않은 것으로 표기한다.
3. 인접한 clique들은 하나의 큰 community로 묶는다.
이때 우리가 정한 k에 따라 다른 결과가 나올 수 있어 여러 개의 k를 시도하는 것이 좋다
그래프 내에서 clique를 찾는 것은 매우 비용이 크므로 작은 그래프에서만 작동한다.