범주형 자료분석

---

1. 적합성 검정 : 하나의 변수에 대해 우리가 기대하는 분포를 따르는지 여부를 검정한다. 즉 기대하는 값과 실제값이 같은지 예측하는 것이다.
2. 동질성 검정 : 두 범주형 변수 사이에서 같은 확률분포를 가지는지 즉 그룹들이 동질한지에 대해 검정하는 것이다.
3. 독립성 검정 : 두 범주형 변수 사이에 상관관계가 있는지를 검정하는 것이다. 즉 표본들이 관찰값에 영향을 주는지 혹은 독립인지 검정하는 것

• 카이제곱검정을 이용한다.
  

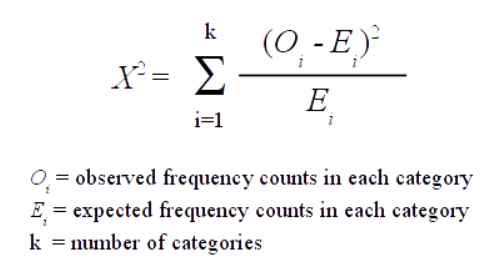
적합성 검정

---

검정통계량

---

$X^2 = \sum_i\frac{(n_i-nP_{i0})^2}{nP_{i0}}=\sum_i\frac{(O_i-E_i)^2}{E_i}$~$X^2(k-1)$

• $O_i$ : 관측도수
• $E_i$ : $H_0$하에서 기대도수

동질성 검정, 독립성 검정

---

검정통계량

---

$X^2 =\sum_i\sum_j\frac{(O_{ij}-\hat E_{ij})^2}{\hat E_{ij}}=\sum_i\sum_j\frac{(n_{ij}-\frac{n_{i+}n_{+j}}{n})^2}{\frac{n_{i+}n_{+j}}{n}}$~$X^2((r-1)(c-1))$

• $O_i$ : 관측도수
• $E_i$ : $H_0$하에서 기대도수

해석

---

독립성검정과 동질성 검정은 검정통계량 식은 같지만 해석하는 부분에는 차이가 있음.
동질성검정 같은 경우 각 확률분포가 같다라는 귀무가설을 세우기에 받아들이게되면 확률분포가 차이가 없다라는 결론을 내린다. 하지만 독립성 검정에서는 이를 보고 관측값은 그룹에 종류에 연관되어있지않다(독립적이다)라는 결론을 내린다. 예를 들어 남자 여자의 흡연비율이 각각 50%로 같다라면 동질성 검정에서 확률분포가 같다라는 결론을 내리고 독립성 검정에서는 이는 성별과는 연관이 없다 독립적이다 라는 결론을 내리게 된다. 반대로 10% 90%로 크게 나뉜다면 동질성은 없고 성별과는 연관성이 있다라는 결론을 내리게 된다.