분산분석(ANOVA)

---

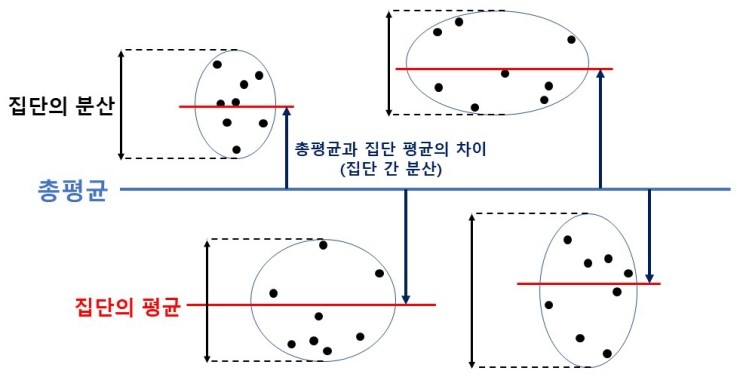
• 여러 개의 다른 모집단의 평균, 분산값을 비교하는 분석기법
• ANOVA의 결과값은 F 통계량이다.
• t-검정의 경우 1-2개의 표본만 비교할 수 있었지만 F-검정의 경우 여러개를 비교할 수 있다.

일원배치 분산기법(one-way ANOVA)

---

• 독립변수 : 이산형, 범주형 변수만 가능
• 종속변수 : 연속형 변수만 가능

모형

---

$Y_{ij} = \mu_i+\epsilon_{ij}$

• i와 j는 각각 그룹과 그 그룹에서 몇번째 표본인지 알려준다.
• $\mu_i$는 i번째 그룹의 평균 값이다
• $\epsilon$은 오차로서 서로 독립이면 정규분포 $N(0,\sigma^2)$를 따른다

관측값 분해

---

$Y_{ij}-\bar Y = (\bar Y_i - \bar Y)+(Y_{ij}-\bar Y_i)$

• $(\bar Y_i - \bar Y)$ : i에서의 측정값의 평균과 전체 평균의 차이 / 쉽게말해 이 그룹의 수준을 보여주는 편차
• $(Y_{ij}-\bar Y_i)$ : 측정값과 그룹의 평균의 차이, i그룹의 정보만으로는 설명할 수 없는 편차

변동의 제곱합

---

• $\sum_i\sum_j(Y_{ij}-\bar Y)^2$ : 총제곱합(SST)
• $\sum_in_i(\bar Y_i - \bar Y)^2$ : 처리제곱합(SStr)
• $\sum_i\sum_j(Y_{ij}-\bar Y_i)^2$ : 오차제곱합(SSE)
• $SSE = SST - SStr$ 을 이용하여 해결

  간편계산식
  $SST = \sum_i\sum_j{y_{ij}}^2-n\bar y^2$
  $SStr = \sum_in_i{\bar y_i}^2-n{\bar y}^2$

자유도

---

• $SST : n-1$
• $SSE : n-k$
• $SStr : k-1$

• $MSE = \frac{SSE}{\sum_{i=1}^kn_i-k}$ : 평균오차제곱

• $Mstr = \frac{SStr}{k-1}$ : 평균처리제곱

분산분석 모형 추론

---

• $H_0$ : k개의 모집단의 모평균의 차이가 없다
• $H_1$ : 모집단의 모든 모평균이 같지는 않다(하나 이상은 차이가난다)
• 모집단의 평균들이 비슷하다면 전체 평균과 모평균들의 차이가 적은 것이라 볼 수 있고 처리제곱합이 작아지지만 평균들이 비슷하지 않다면 처리제곱합은 커지게 된다.
• $F = \frac{Mstr}{MSE} ~ F(k-1,n-k)$
• $F$값이 크단말은 평균간의 차이가 난다는 의미이고 귀무가설을 기각할 확률이 높아진다