
다이나믹 프로그래밍?
다이나믹 프로그래밍, 줄여서 dp라고도 부르는 이 말은 알고리즘 문제를 풀때 최소한 한번쯤은 들어봤을만한 말이다. 필자의 경우는 피보나치 관련해서 백준 문제를 풀다가 막혀서 질문 게시판에서 처음으로 접한 단어이다. 막상 찾아보니 개념 자체는 그렇게 어렵지 않았다. 그냥 한번 계산한 결과는 저장해뒀다가 나중에 다시 써먹는 것. 똑같은 일 두번 하는거 싫어하는 스타일이라고 보면 된다.
dp는 왜 쓰는걸까?
음..필자의 현재 백준 티어는 실버 2지만, 한창 브론즈였던 시절에는 시간 복잡도가 그렇게 중요하지 않았다. 그냥 문제 그대로 해석해서 코드로 표현하면 그게 정답이고 그게 문제를 푸는 방법이였다. 하지만 티어가 올라가고 문제 난이도가 높아지면서 점점 시간 초과가 많이 생기기 시작했고, 왜 안풀릴까 생각하며 슬럼프에도 빠지기 시작했다. 본론으로 돌아와서,, dp는 처음에 말했던 것처럼 '한번 계산한 결과는 저장했다가 나중에 다시 써먹는 것'이다.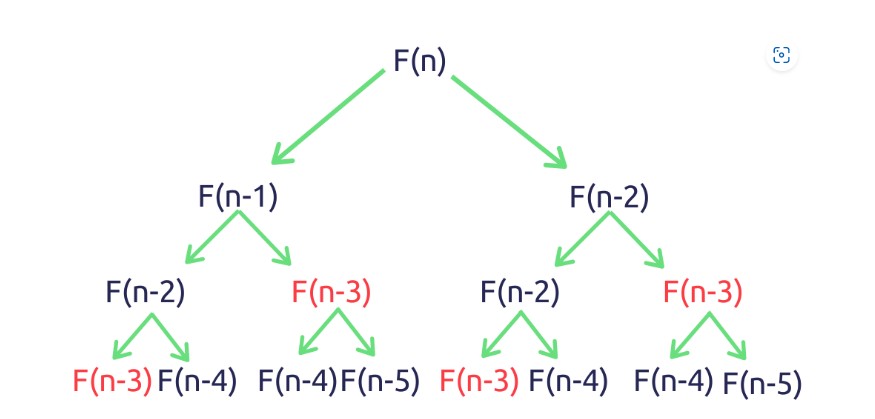
피보나치 수열을 예시로 들자면 문제를 쪼개면서 중복이 되는 계산들이 점점 보이기 시작한다. "F(n-3)은 아까도 했는데 또 해?" 사람이 풀어도 귀찮은데 컴퓨터는 오죽할까,, 그래서 한 번 계산한 결과를 저장해두고 다시 써먹으면 굳이 계산을 두번 세번 할일이 없어서 시간 복잡도 면에서 이득을 볼 수 있다.
그래서 dp 쓰면 얼마나 좋은데?
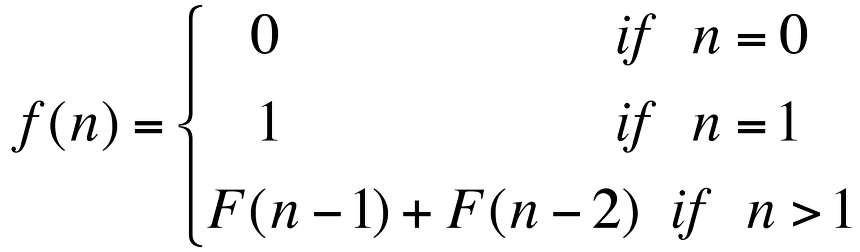
피보나치 함수의 점화식이다. 0일땐 0, 1일땐 1, 2 이상부터는 n 전수와 전전 수를 더한 값이 구하고자 하는 피보나치 수이다. 10번째 피보나치 수를 구하고 싶다면 9와 8의 피보나치, 다시 8, 7과 7, 6... 내려가다 보면 1인 순간일때 1부터 다시 더해가며 쌓아가는 것이다. 이 식을 코드로 표현하면 다음과 같다.
int fibo(int n){
if (n == 0) return 0;
else if (n == 1) return 1;
else return fibo(n-1) + fibo(n-2);
}함수를 한번 호출할때마다 두개씩 쪼개져서 재호출됨으로 빅오 표기법으로는 O(2^n)이다. 그런데 여기서 n으로 50이 들어온다면?
dp를 이용한 코드에서는 12586269025 라는 숫자가 금방 나왔지만 저 코드대로 돌렸더니 냉장고에서 오렌지 주스 한잔 꺼내먹어도 돌아가길래 그냥 꺼버렸다....
말하고자 하는 바는 "dp를 사용하면 이정도로 빠르다!"이니 알아들었으면 됐다.
dp의 조건?
dp는 다음 두가지 조건을 갖추고 있어야 작동한다.
1. 큰 문제를 쪼개었을때 겹치는 작은 문제들이 있는가?
2. 작은 문제에서 푼 정답은 큰 문제에서도 똑같은가?
예시로 자꾸 피보나치 수열만 들먹이는것 같지만,, 피보나치가 설명하기 제일 쉬운것 같아서 계속 주제로 써먹을 예정이다.
f(50)이라는 수는 f(49) + f(48)로 쪼갤수 있고, 또 각각의 수들은 f(48)+f(47), f(47)+f(46)...계속해서 쪼개면서 중복되는 작은 수들이 보인다. ex) f(47) 같은.
두번째, 피보나치 수열에서 어떤 수가 됐던 간에 결국 f(n-x)가 1까지 갈 수 밖에 없다. 결국 f(1) = 1이므로 쪼개서 풀었던 작은 문제의 답이 큰 문제에서도 동일하므로 두번째 조건도 맞아떨어진다.
피보나치 수열이 dp로 풀기 좋은 이유는 위 두가지 때문이다.
기록하기
dp는 한번 계산한 값을 저장해놓고 필요할때 다시 써먹는다고 말했다. 이 행위를 Memoization이라고 부른다. 우리가 8x9를 할때마다 8+8+8+...를 하지 않고 구구단을 외워서 바로 72가 나오는것처럼, dp에서도 계산한 결과를 어딘가에 저장해두어야 한다.
Top-down 방식
하향식이라고도 불리는 이 기법은 위에서 시작해서 끝까지 내려간 다음에 그 결과값을 가지고 재귀적으로 타고 올라간다고 생각하면 된다.
코드로 나타내보면 다음과 같다.
int arr[10000] = {0,};
int fibo(int n) {
if (n <= 1) return n;
else{
if (arr[n] != 0) return arr[n];
arr[n] = fibo(n-1) + fibo(n-2);
return arr[n];
}
}n이 1이 나오면 n을 리턴(1을 리턴) 해주고, 아니면 배열에 저장된 값이 있는지 살펴본 후, 그것도 없으면 함수를 다시 호출하면서 차근차근 내려가며 배열에 하나하나 쌓는 방식이다.
Bottom-up 방식
상향식이라고도 불리는 바텀-업 기법은 가장 작은 문제를 해결하면서 최종적으로 가장 큰 문제를 해결하는 방식이다. 이것 역시 코드로 나타내면 다음과 같다.
int arr[10000] = {0, 1};
int fibo(int n) {
for (int i = 2; i < n + 1; i++) {
arr[i] = arr[i - 1] + arr[i - 2];
}
return arr[n];
}첫번째 피보나치 수는 0, 두번째 피보나치 수는 1이라고 알려주고 for문을 돌려가며 배열에 저장하고, 구하고자 하는 n번째 피보나치 수까지 올라가는 방식이다.
탑다운과 바텀업..누가 더 쎌까?

사실 케바케다. 필자는 바텀-업 방식을 주로 사용하지만 상황에 따라서는 오히려 탑-다운이 빠른 경우도 있다. 다이나믹 프로그래밍은 많이 풀어보고 경험을 쌓는게 더 중요하다고 생각한다.
마무리
정리하는걸 귀찮아하며 살아왔습니다. 하지만 이렇게 공부한 내용을 메모해보니 더 기억에 남는다는 걸 알았고, 앞으로는 배운 내용을 이렇게 글로 정리해서 올려볼 생각입니다. 부족한 점이나 틀린 부분은 댓글로 알려주시면 감사하겠습니다.
