그리디 알고리즘?
Greedy == 탐욕스러운, 욕심 많은
욕심 많은 알고리즘, 한국에서는 탐욕법이라고도 부른다.
그리디 알고리즘(욕심쟁이 알고리즘, Greedy Algorithm)이란 "매 선택에서 지금 이 순간 당장 최적인 답을 선택하여 적합한 결과를 도출하자"라는 모토를 가지는 알고리즘 설계 기법이다.
나무위키에서는 그리디 알고리즘을 이렇게 설명하고 있다.
최적의 답을 선택하는것이 감이 잘 안 올수 있어서 한번 예시를 들어보고자 한다.
그리디한 선택
지금 당신의 눈 앞에 문이 3개가 있다. 문 앞에는 동전 더미, 1만원 권 지폐 몇장, 5만원 다발이 놓여있다. 선택한 문 앞에 있는 돈을 가지고 갈 수 있고, 문 너머에 뭐가 있을지는 모른다. 당신은 어떤 문을 고를 것인가? 동전? 5만원?
아마 보통 사람이라면 5만원 다발이 있는 문을 고를 것이다. 나같아도 5만원 다발이 있는데 눈이 안 돌아갈 수가 없다.

알고보니 문 너머에는 폭탄이 설치돼있어서 여는 순간 죽는 엔딩이였다는거임...
만약 두번째 문을 골랐더라면 5만원권을 엄청 챙겨서 부자가 될 수 있었겠지만, 문 앞에 우리는 그걸 알수 있었을까?
이처럼 각 순간순간마다 최적의 선택을 하는 알고리즘이지만, 그 선택이 무조건 정답이라고 할 수 없는것이 그리디 알고리즘이다.
이러면 얘는 어디에 씀?
방금 예시는 너무 극단적이여서 그렇지 그리디 알고리즘은 사실 꽤나 효율적인 알고리즘이다.
단 아래의 조건을 갖춘 상태에서 그리디 알고리즘을 사용해야 한다.
-
최적 부분 구조를 가지고 있을 때
DP처럼 문제를 작게 쪼개고 쪼갠 문제의 정답이 곧 큰 문제의 정답일 때이다.
DP가 궁금하다면 --> 감히 쪼개? 문제 주제에 뭔데 -
탐욕적 선택 속성을 가지고 있을 때
그리디한 선택이 항상 최적해를 보장할 때이다.
피보나치 수열을 예시로 들어보자면,F₁ = 1
F₂ = 1
Fn = Fn-₁+ Fn-₂ (n>=1)피보나치 수열의 점화식에서 Fn은 Fn-₁ 과 Fn-₂의 합으로 이루어져 있다.
이처럼 전 수와 전전 수에 따라서 Fn이 결정되는데, 이 과정을 거치기 위해서는 F₁과 F₂를 알고 있고, 한단계 한단계 모두 더해서 피보나치 수를 만들어야 하기 때문에 이런 경우는 탐욕적 선택 속성을 가지고 있지 않다고 말한다. 그리디 알고리즘과 dp의 차이점이라고도 할 수 있다.
모든 부분을 탐색하지 않기 때문에 두 조건을 갖춘 상태에서는 준수한 속도를 보여주는 알고리즘이다.
알고리즘 문제에서 그리디를 사용해보자
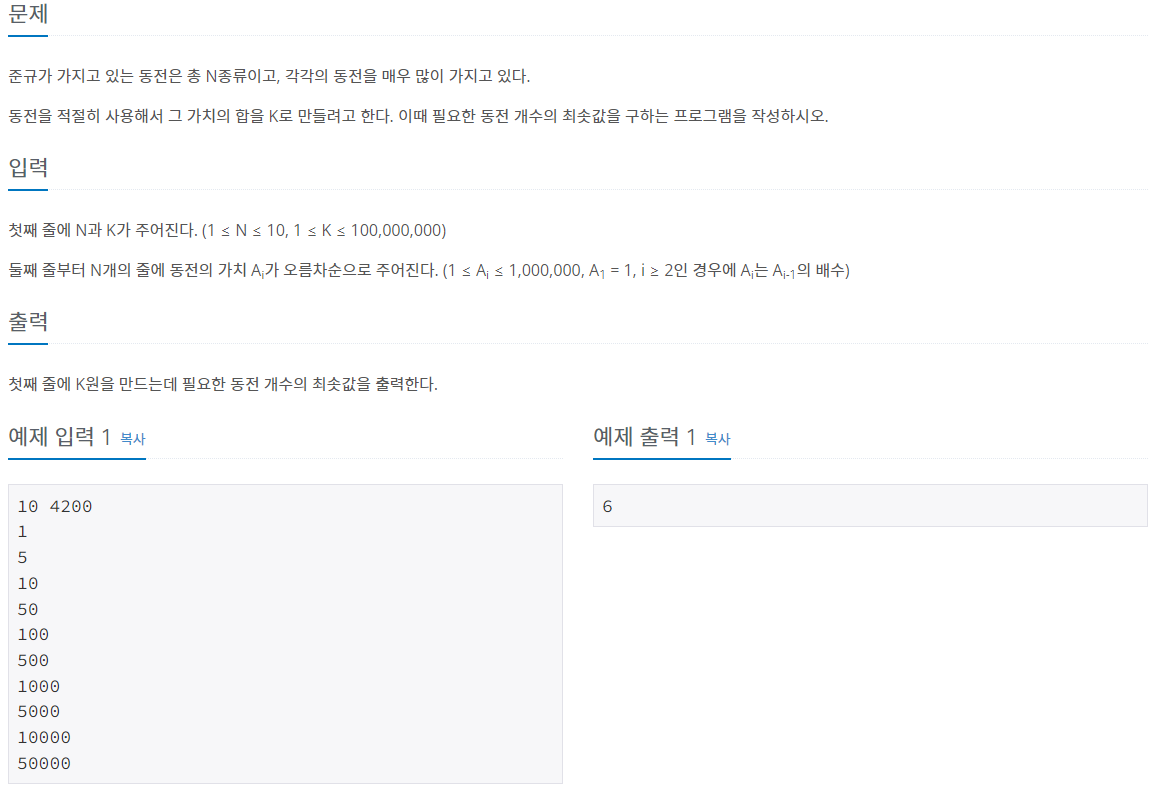
그리디 알고리즘의 대표격인 동전 문제를 풀어보자
문제를 먼저 풀어보고 싶은 사람은 여기로 -->동전 0
n개만큼 동전의 갯수가 주어진다. 이때 각 동전의 가치는 전에 입력한 동전의 가치의 배수이고, 이 동전으로 k원을 만들 때, 동전을 최대한 적게 사용하는 문제이다.
4200원에서 1원을 10번 쓰는것은 10원을 한번 쓰는것과 같고, 10원을 10번 쓰는것은 100원을 한번 쓰는것과 같기 때문에 이 부분에서 최적 부분 구조를 이루고 있다. => 조건 1 성립
4200원에서 1000원을 4번 빼면 2백원이 남고, 이 경우는 100원짜리를 40번 쓰는것과 같다. 고로 굳이 100원을 40번 빼보지 않아도 최적의 해를 구할 수 있다. => 조건 2 성립
언뜻 보면 비슷한 말 같지만 의미 파악을 잘 해야 한다.
문제를 풀어보자면 k보다 작으면서 가장 가까운 수를 빼는것이 그리디한 선택이자 최적해를 구하는 방법이고, 이를 코드로 나타내보면 다음과 같다.
그리디 알고리즘을 사용해 11047번 풀어보기
#include <stdio.h>
int main() {
int n , k, coin[10], index = 0, count = 0;
scanf("%d %d", &n, &k);
for (int i = n - 1; i >= 0; i--) {
scanf("%d", &coin[i]);
}
while (k > 0){
count += k / coin[index];
k %= coin[index];
index++;
}
printf("%d", count);
return 0;
}coin[10]은 동전의 가치를 저장할 배열, count는 우리가 구해야 할 동전의 갯수를 저장할 변수이다.
n - 1 부터 n >= 0까지 입력을 받는 이유는 단순히 처음부터 큰 값으로 뺀 값이 그리디한 선택이므로 빼기 편하게 입력을 받았다. (입력받은 배열을 뒤집었다고 생각하자)
while문을 돌면서 coin[index]만큼 k를 나눠주고 그 몫을 count 변수에 더한다.
index가 0일때부터 시작하면 count = 0 + 4200/50000 이라서 count에는 0이 더해지고, k %= coin[index]도 k = (4200 / 50000 의 나머지) = 0 이여서 k값도 그대로이다.
결국 k보다 작은 수가 나오기 전까지는 index만 늘어나면서 while문을 돌린다.
index가 3이 되는 순간 count = 0 + 4200 / 1000 = 0 + 4 = 4, count는 4가 된다.
4200 / 1000은 4200에서 1000을 4번 뺀 것과 마찬가지이므로 4가 더해지고, 그만큼 k에서 빼줘야 하니까 k %= 1000을 하면 4200 - 4000 = 200 이 된다.
다시 500.. 100이 되면 count = 4 + 200 / 100 = 4 + 2 = 6이 되고, k = 200 % 100 = 0이 되서 while 문이 끝나고 6을 출력하는것이다.
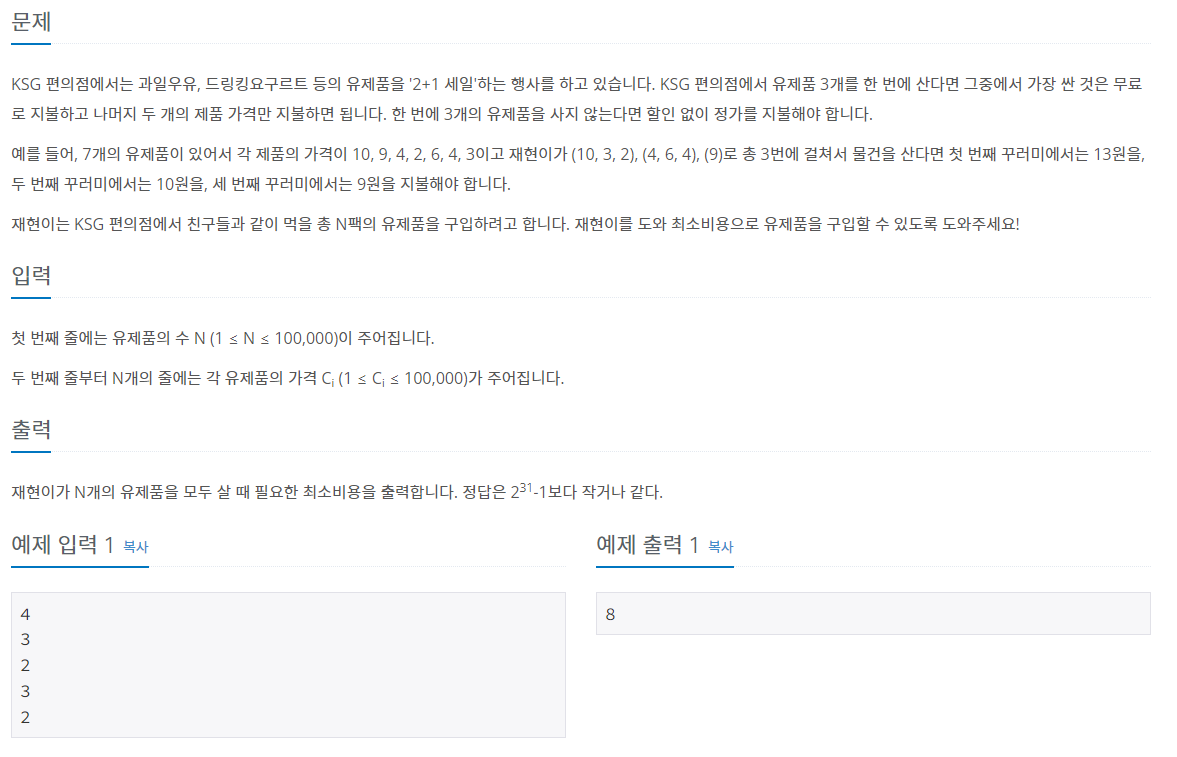
그리디 알고리즘을 사용해 11508번 풀어보기
문제를 먼저 풀어보고 싶은 사람은 여기로 -->2 + 1 세일
유제품 수 n이 주어지고, n개의 유제품들 중에서 3개를 고른 후 그중 하나는 무료로, 두개는 돈을 주고 구매할 때, n개 모두 살때 최소비용을 구하는 문제이다. 이때 무료로 지불하는 금액은 가장 싼 유제품의 금액이다.
그리디하게 생각해보면 비용을 제일 적게 만드는 방법은 가장 가격이 높은 유제품을 무료로 지불하는 것이다. == 정렬을 시켜서 3개씩 묶는다.
10, 9, 4, 2, 6, 4, 3을 예로 들면 정렬 후에는 2, 3, 4, 4, 6, 9, 10이고,
이는 [2], [3, 4, 4], [6, 9, 10], 2 + 8 + 19 = 29원이다. (최소 비용)
필자가 쓴 코드는 다음과 같다.
#include <stdio.h>
#include <stdlib.h>
int comp(const void *a, const void *b) {
return *(int *) a - *(int *) b;
}
int main() {
int n, arr[100000], sum = 0;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &arr[i]);
}
qsort(arr, n, sizeof(int), comp);
n--;
while (n > 1) {
sum += arr[n] + arr[n - 1];
n -= 3;
}
while (n >= 0) {
sum += arr[n];
n--;
}
printf("%d", sum);
return 0;
}qsort를 활용해 배열의 값을 정렬하고, 뒤에서부터 큰 값 3개씩 묶어서 sum에 더해준다. 이때 가장 싼 유제품이 무료이므로 sum += arr[n] + arr[n-1] 까지만 해준다.
그 후에 n -= 3을 통해 3개씩 제거하면서 내려간다.
while문이 1부터 멈추는 이유는 3개씩 묶이지 않는 상황을 피하기 위함이다. 만약 8개를 구매한다면?
배열은 0번째 인덱스부터 시작하니까 가장 큰 값이 있는 인덱스 7부터 시작해서 7-> 4-> 1에서 멈춘다.
남은 두 유제품은 다음 while문에서 arr[0]까지 가격을 더해주면 최소 비용이 완성된다.
마무리
필자를 처음에 그리디 알고리즘을 접하고 문제를 풀었을 때 이런 생각이 들곤 했다.
"너무 내 멋대로 푸는거 아닌가..?"
"이걸 알고리즘이라고 할 수 있나?"
사실 앞서 풀어본 두 문제도 형식이 정해져 있지는 않다.
정형화된 방법이 있는 dp와는 다르게 뭔가 딱히 "이런 방식이 있다~" 같은게 없어서 이해하는데 좀 어려울 수 있지만, 그리디는 결국 상황에 따라 최대한 이득을 볼 수 있는 구조로 그리디한 사고방식을 기르는게 중요하다는걸 말하고 싶다.




This article is really amazing. Thanks for the sharing.
GMGlobalConnect VSP