파스칼의 어마무시한 삼각형

생김새

'파스칼의 삼각형' 이란 단어는 언뜻 봐서 우리에게 공포감을 조성할 수 있다. 처음 들었을땐 엄청 어려운 개념인가 했지만 사실 우리는 어릴때 파스칼의 삼각형을 배우고 왔다.

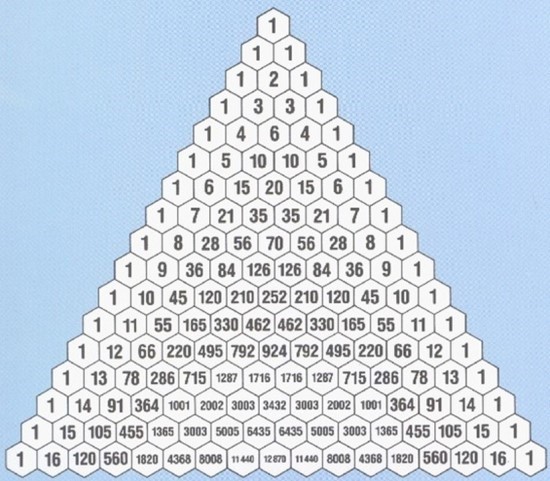
얘가 걔다. 초등학교 4학년쯤 배웠던거 같은데 나름 알고 나니 전혀 무섭지 않다. 어렸을 때는 규칙 찾기 느낌으로 수업을 들었었지만, 지금은 조합을 섞어서 한번 알아보고자 한다.

성질

각 행의 숫자들을 모두 더하면 2의 제곱수가 된다.

1행 : 1 + 1 = 2 ^ 1
2행 : 1 + 2 + 1 = 2 ^ 2
3행 : 1 + 3 + 3 + 1 = 2 ^ 3
4행 : 1 + 4 + 6 + 4 + 1 = 2 ^ 4

행이 내려갈수록 점진적으로 지수가 올라가는 규칙이 있다.

양쪽 수를 더한 값이 바로 아래쪽에 있는 숫자가 된다.

ex) 20 + 15 = 35, 15 + 6 = 21

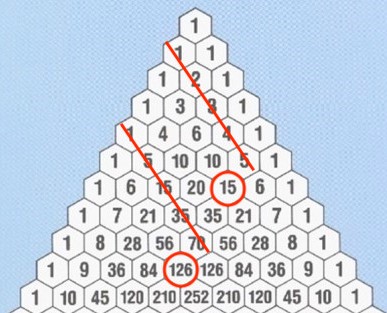
1에서 시작한 대각선의 수의 합은 마지막 수와 접한 수랑 같다.

1 + 2 + 3 + 4 + 5 = 15
1 + 5 + 15 + 35 + 70 = 126
왼쪽에서 타고 내려온 경우에는 마지막 수의 왼쪽으로 접한 수,
반대의 경우는 오른쪽으로 접한 수가 합과 같다.

규칙이 하키 스틱과 닮아서 하키 스틱 패턴이라고도 부른다.

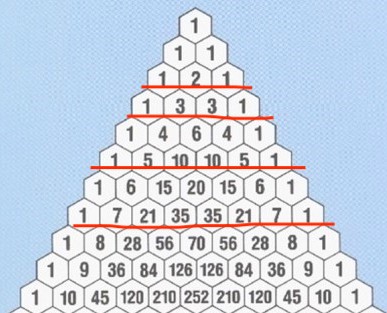
파스칼 삼각형의 소수 열에 있는 숫자들은 각 소수의 배수들이다.

2, 3, 5, 7 부분의 숫자들은 모두 각 수의 배수들이다.

그 외에도 가운데를 기준으로 잘라보면 대칭이 나온다던가, 대각선으로 라인을 타서 보면 삼각수, 사면체수 등이 나온다던가 여러 성질이 있다.

파스칼 삼각형과 조합

파스칼 삼각형의 어느 부분에서든 이 규칙이 통한다. 그렇다면 이걸 조합 측면으로 접근한다면 파스칼 삼각형은

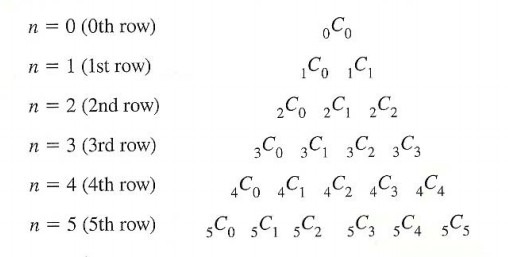
이런 식으로 나타낼 수 있고, 이것은 앞서 나온 규칙을 적용하여

nCr = n-1 C r + n-1 C r-1

위 식이 성립함을 보여준다.

파스칼 삼각형의 양쪽 끝이 모두 1인 이유도 nCn = nC0 = 1 때문인데, 이것은 다음과 같다.

5가지중 5가지를 모두 뽑는 경우의 수는 한가지 밖에 없기 때문에 5C5 = nCn = 1이고,
5가지중 하나도 뽑지 않는 경우도 한가지밖에 없기 때문에 5C0 = nC0 = 1이다.

파스칼 삼각형이 가운데를 기준으로 대칭인 이유도 nCr = nCn-r이기 때문이다.

3C1과 3C2을 예로 들면
3C1 = 3가지중 한개를 뽑는 경우 = 3개
3C2 = 3가지중 두개를 뽑는 경우 = [1, 2], [2, 3], [1, 3] = 3개

좀 이해가 안되는 부분이 있다면 필자가 예전에 쓴 조합 관련 글을 읽어보고 오는걸 추천한다.
--->로또 1등을 할 수 있는 경우의 수

알고리즘 문제에서 파스칼 삼각형을 사용해보자

파스칼 삼각형을 이용하는 백준 11051번 문제를 풀면서 필자의 코드를 이해해보자.

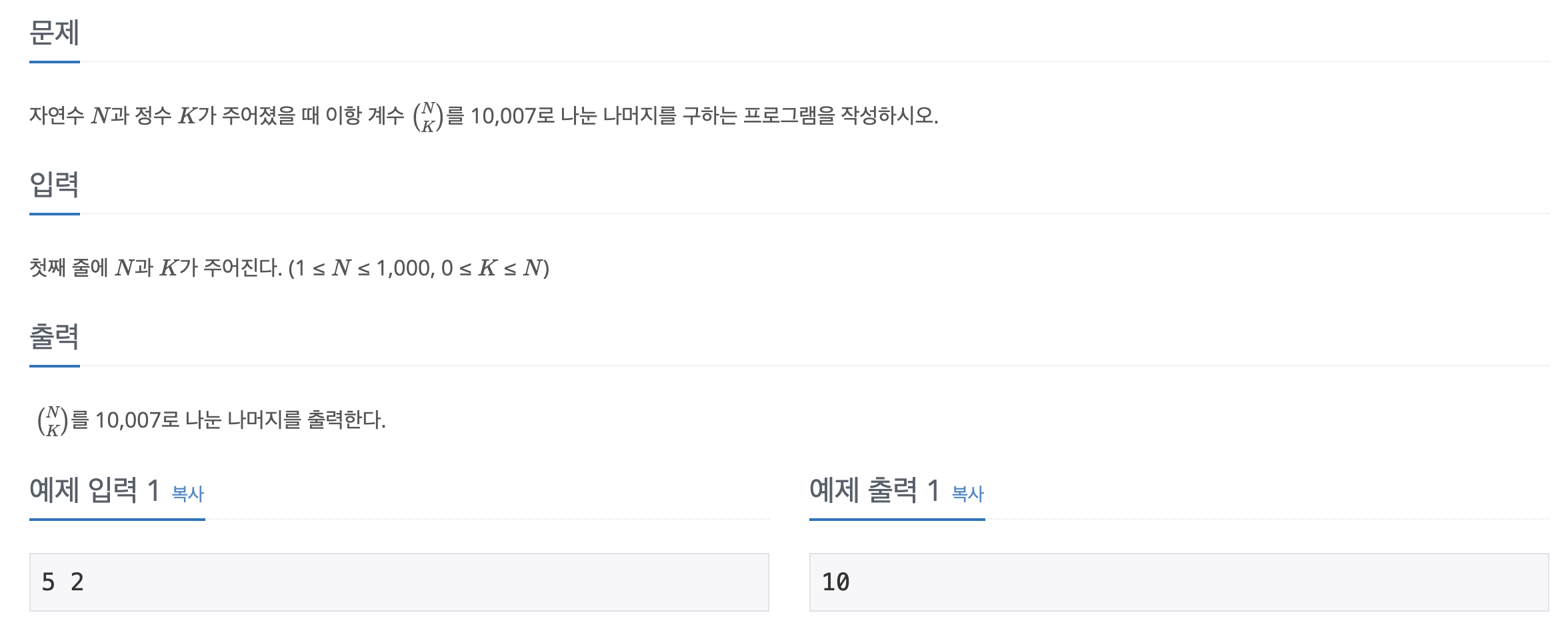
문제를 먼저 풀어보고 싶은 사람은 여기로 --> 11051번: 이항 계수 2

문제에서 어려운 점은 이항 계수를 구했을 때 10007로 나눈 나머지를 구하라는 것이다.
파이썬같이 임의 정밀도를 지원하는 언어를 제외하고는(= 정수형 제한이 없는) 다 구한 후 10007로 나누기 전에 이미 숫자 범위가 long long int를 한참 초과해버린다.
이 문제를 해결하기 위해 파스칼 삼각형은 dp로 구현하면서, 미리미리 10007로 나눈 나머지를 저장해두며 top-down 방식으로 숫자를 찾아나가도록 설계했다.

dp에 대한 자세한 설명이 궁금하다면 ----> 감히 쪼개? 문제 주제에 뭔데?

파스칼 삼각형을 dp로 나타내는 방법은 삼각형을 왼쪽으로 싹 다 밀면

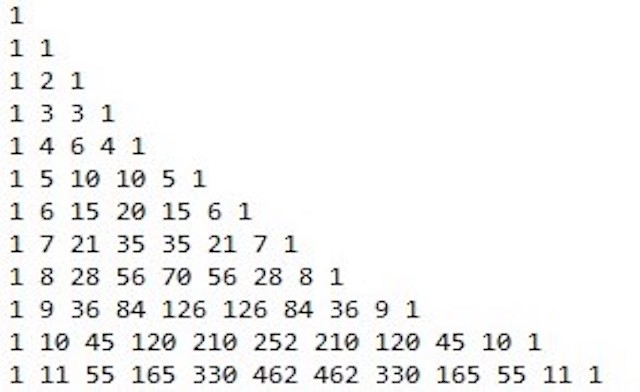
이렇게 나오고, 2차원 배열을 만들어서 각각 저장하면 된다.
nCn = nC0 = 1을 함수의 종료 조건으로 잡고, 배열에 nCr = n-1 C r + n-1 C r-1을 넣어주면서 재귀호출을 하면 n과 k의 이항계수를 구할 수 있다.

top-down 방식으로 11051번 풀어보기

#include <stdio.h>

int arr[1001][1001];

int topDown(int n, int k) {
    if (n == k || k == 0) return 1;
    else {
        if (arr[n][k] != 0) return arr[n][k];
        arr[n][k] = (topDown(n - 1, k) + topDown(n - 1, k - 1)) % 10007;
        return arr[n][k];
    }
}

int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    printf("%d\n", topDown(n, k));
    return 0;
}

if문에 1을 리턴하도록 종료조건을 달아서 삼각형의 맨 바깥쪽을 1로 만들어주고, 이항계수 공식을 이용해 arr[n][k]에 넣어주고 10007로 나눈 나머지를 넣어주면 손쉽게 문제를 해결할 수 있다.

bottom-up 방식으로 11051번 풀어보기

혹시라도 바텀업 방식이 궁금한 사람들을 위해 한번 코드를 짜보았다.

#include <stdio.h>

int arr[1001][1001];


int bottomUp(int n, int k) {
    arr[0][0] = 1;
    arr[1][0] = 1;
    arr[1][1] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= i; j++) {
            if (j == 0 || i == j) arr[i][j] = 1;
            else arr[i][j] = (arr[i - 1][j] + arr[i - 1][j - 1]) % 10007;
        }
    }
    return arr[n][k];
}

int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    printf("%d\n", bottomUp(n, k));
    return 0;
}

먼저 맨 위에 있는 1들을 초기값으로 지정해주고, for문을 돌면서 파스칼 삼각형을 만들어간다. 두번째 for문이 i까지 도는 이유는

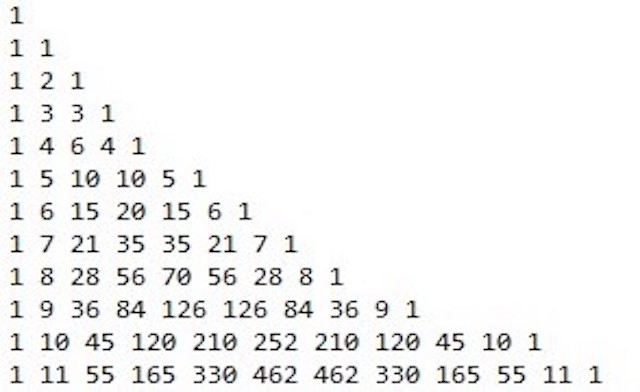
파스칼 삼각형은 i(행)가 증가할수록 j(열)이 길어지기 때문에 i에 비례해서 늘어나도록 적어주고, if문에는 top-down 처럼 nCn = nC0 = 1을 넣어주면 bottom-up 방식의 파스칼 삼각형도 만들 수 있다.

마무리

물론 파스칼 삼각형을 이용하지 않고도 문제를 해결 할 수는 있다. 다만 주제가 파스칼 삼각형인 만큼 얘를 이용해 풀었다는걸 감안하고 봐줬으면 좋겠다.