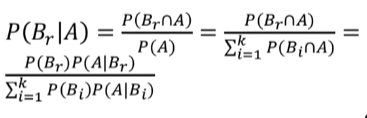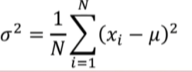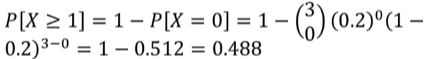TIL#8-1

2주차 Day4

오늘은 확률, 확률분포 가 주를 이룬 강의다

조합(Comination)

(출처:프로그래머스 인공지능 수학 강의 중)

베이즈 정리

확률분포

확률 변수(random variable)

• 랜덤한 실험 결과에 의존하는 실수
  • 즉 표본 공간의 부분 집하에 대응하는 실수
• 주사위 2개를 던지는 실험
  • 주사위 숫자의 합: 하나의 확률변수
  • 주사위 숫자의 차: 하나의 확률변수
  • 두 주사위 숫자 중 같거나 큰 수: 하나의 확률 변수
• 이산확률변수
  • 확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우(ex:주사위, 동전과 예)
• 연속확률변수
  • 셀 수 없는 경우(ex: 학교에서 랜덤하게 선택된 남학생의 키)

이산확률 변수의 확률분포

• 확률변수 X가 x라는 값을 가질 확률
  • P(X = x) = f(x)
  • 확률질량함수
    ex) 확률 변수 X가 가질 수 있는 값:0,2,5
    P(X=x) = f(x) = $\frac{x+1}{10}$
    P(X=0)=0.1, P(X=2)=0.3, P(X=5)=0.6
• 
• 이산확률변수의 분산:
  • 실험을 할 때마다 확률변수의 값이 달라질 수 있음 따라서 변동의 정도인 분산을 계산할수 있음.
    

확률변수 X의 분산: 간편식

$E(X)^2 - {E(x)}^2$

이항분포

• 베르누이 시행
  • 정확하게 2개의 결과만을 가지는 실험(ex:동전던지기)
  • 성공의 확률: p
• 확률변수 X
  • n번의 베르누이 시행에서 성공의 횟수
  • 이항확률변수 라고 함
• 이항분포
  • 이항확률변수의 확률분포
    ex: 어떤 랜덤박스의 뽑기 성공 확률이 0.2 이다.
    3개를 뽑았을 때, 적어도 하나 이상의 성공이 발생할 확률은?
    

#파이썬에서 이항롹률변수의 확률분포 계산하기
form scipy import stats
1-stats.binom.cdf(0, n=3, p=0.2)
==>  0.48799999999 #실행결과

이항분포의 평균, 분산, 표준편차

stats.binom.stats(n=3, p=0.2)
==> (array(0.6, array(0.48)) #으로 출력

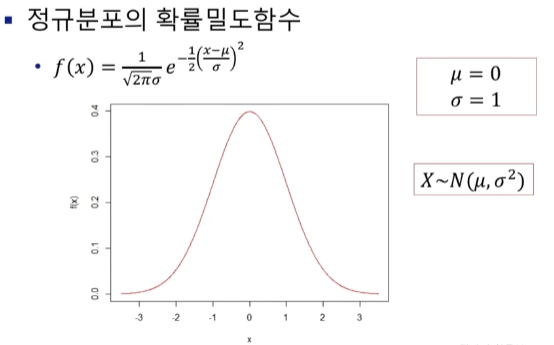
정규분포

• 연속확률 변수의 확률 분포