📍 변분 추정(Variational Inference)
생성형 모델에서는 어떤 관측 데이터 x가 있다고 할 때,
그걸 만든 잠재 변수 z를 찾고 싶습니다.
우리가 하고 싶은 일
Posterior(사후확률)인 p(z | x) 를 구하는 것, 하지만 대부분의 경우 이 확률은 계산이 불가능하거나 너무 복잡합니다.
p(z | x)를 직접 계산할 수 없으니,
대신 계산 가능한 근사 분포 q(z|x) 를 만들고 이걸 학습하자!
즉,q(z | x) ≈ p(z | x) 가 되도록
q를 최적화(함수의 형태를 조정) 하는 방법이 변분 추론(variational inference) 입니다.
우리는 q(z|x)라는 근사 분포를 설계하고,
그게 진짜 분포 p(z|x)와 가깝도록 학습시키고 싶습니다.
1️⃣ 사전확률
사전 확률(pre-priori probability)은 특정 이벤트가 일어나기 전에, 그 이벤트가 일어날 확률을 말합니다. 이러한 확률은 과거의 데이터, 경험, 또는 전문가의 지식을 바탕으로 추정됩니다.( ex. 전체 메일중 20%가 스팸라면, 사전확률은 0.2이다)
2️⃣ 사후 확률
사후 확률(posterior probability)은 새로운 정보나 증거가 주어진 후에, 특정 이벤트가 일어날 확률을 업데이트한 것을 말합니다. 이 확률은 사전 확률에 새로운 증거를 통합하여 계산됩니다.
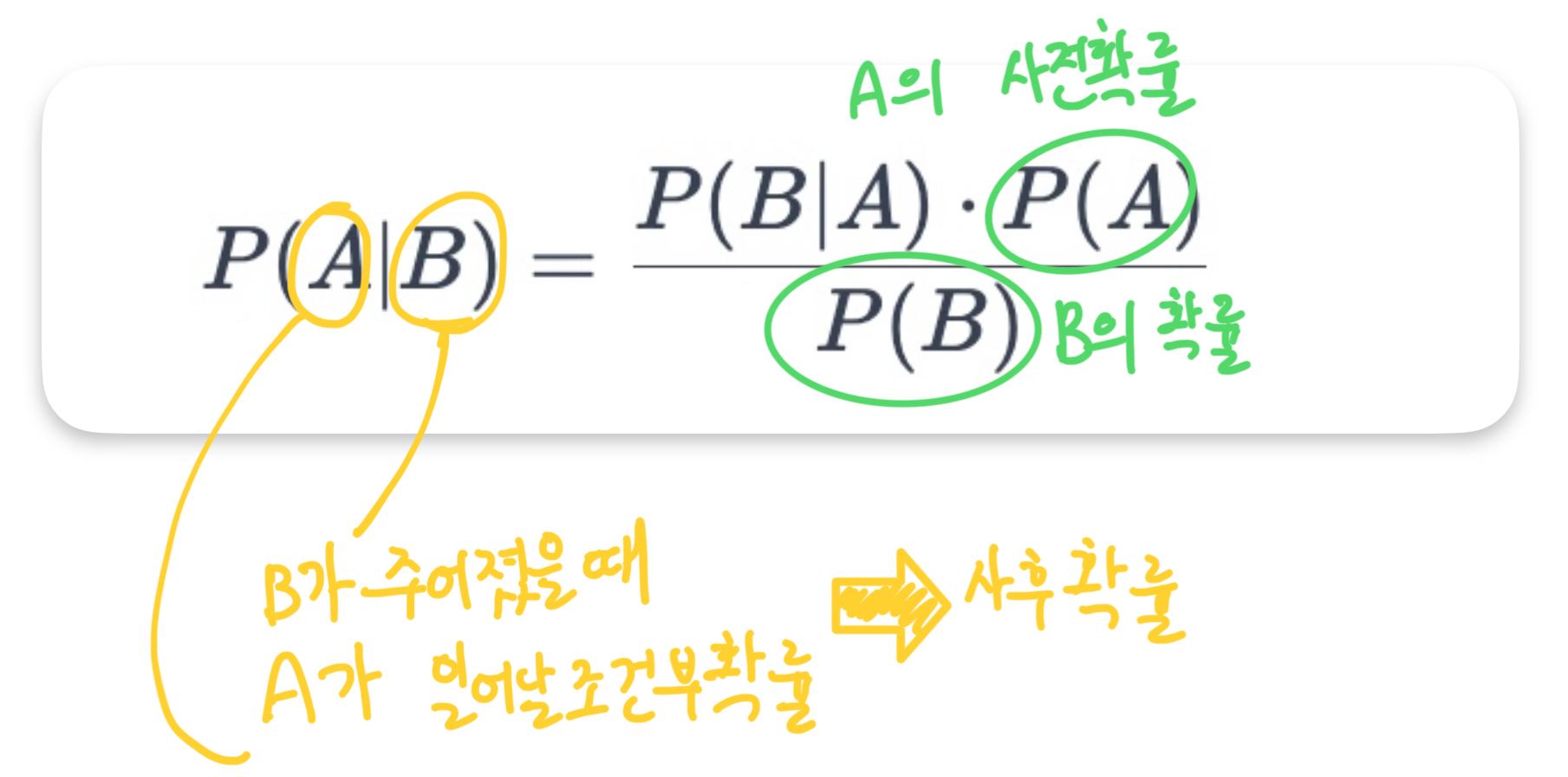
- P(A∣B)
P(A∣B)는 B가 주어졌을 때 A가 일어날 조건부 확률, 즉 사후 확률입니다.- P(B∣A)
P(B∣A)는 A가 주어졌을 때 B가 일어날 조건부 확률,- (A)
P(A)는 A의 사전 확률, 그리고- P(B)
P(B)는 B의 확률입니다.
[참고문헌]