알고리즘에서도 느끼는 거지만 Tree 구조가 정말 중요한 것 같다. 앞으로 랜덤 포레스트의 기본 구성 요소가 결정 트리라고 하니 잘 정리해 보려고 한다!

결정 트리는 분류와 회귀 작업, 다중 출력 작업까지 가능한 ML 알고리즘이다.

🔥6.1~6.2 결정 트리 학습과 시각화, 예측

이해를 위해 모델을 하나 만들어서 예측하는 방법에 대해 알아보았다.

# Train DecisionTreeClassifier on the iris dataset
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier

iris = load_iris(as_frame=True)
X_iris = iris.data[["petal length (cm)", "petal width (cm)"]].values
y_iris = iris.target

tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf .fit(X_iris, y_iris)

아래와 같이 결과가 나왔다.
DecisionTreeClassifier(max_depth=2, random_state=42)

from sklearn.tree import export_graphviz

export_graphviz(tree_clf, 
                out_file="iris_tree.dot", 
                feature_names=["꽃잎 길이(cm)", "꽃잎 너비 (cm)"],
                class_names=iris.target_names,
               rounded=True,
               filled=True)

from graphviz import Source

Source.from_file("iris_tree.dot")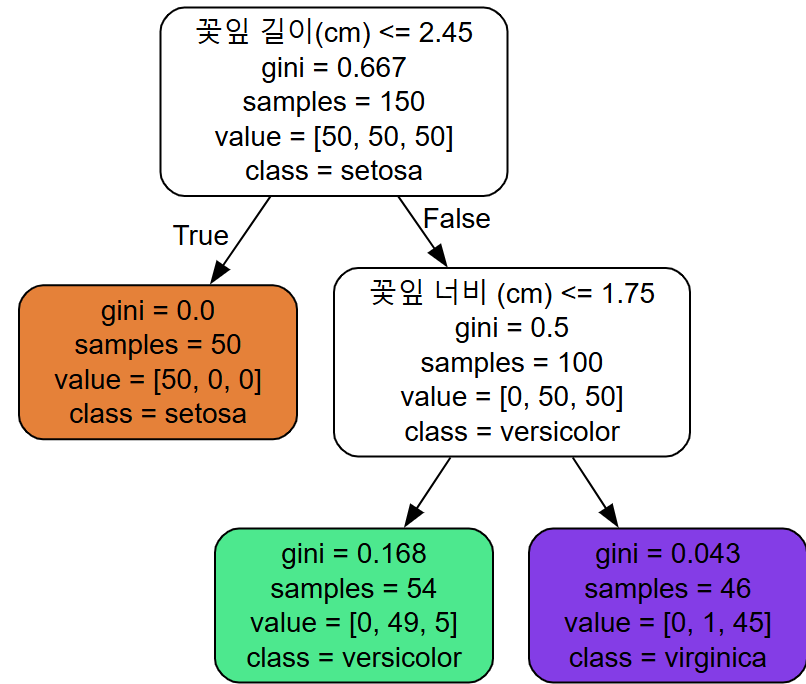

결과로 나온 트리의 구조를 보면, 트리가 어떻게 예측을 하는 지 알 수 있다.

ex) 깊이 2의 왼쪽 노드
value값이 뜻 하는 것
Iris-Setosa : 0% (0/54)
Iris-Versicolor : 90.7%(49/54)
Iris-Virginica : 9.3%(5/54)

만약 클래스를 예측한다면? → 가장 확률(90.7%) 높은 Iris-Versicolor 출력

지니 불순도

한 노드의 모든 샘플이 같은 클래스에 속해 있다면 이 노드는 순수(gini=0) 하다고 한다.

$G_i$는 $i$번째 노드의 지니 불순도
$p_{i,k}$는 $i$번째 노드에 있는 훈련 샘플 중 클래스 $k$에 속한 샘플의 비율

엔트로피

모든 메시지가 동일할 때 엔트로피=0
메시지의 평균 정보량을 측정하는 섀넌의 정보이론도 이에 해당

DecisionTreeClassifier 클래스는 지니 불순도 사용
❗다만❗ criterion="entropy" 로 지정하여 엔트로피 불순도 사용 가능

지니 불순도 vs 엔트로피

실제로는 큰 차이가 없다고 한다.
지니 불순도 특징 : 계산이 더 빠름, 단 빈도 높은 클래스를 한쪽 branch로 고립시키는 경향 있음.
엔트로피 특징 : 조금 더 균형 잡힌 트리를 만듦
→ Sebastian Raschka 분석

🔥6.4 CART 훈련 알고리즘

• 훈련 세트를 하나의 특성 $k$와 임곗값 $t_k$를 사용해 두 개의 서브셋으로 나눈다.

  • 이 때 가중치가 적용된 가장 순수한 서브셋으로 나눌 수 있는 $(k, t_k)$ 쌍을 찾는다
  • 이 쌍을 구하기 위해 최소화해야 하는 비용 함수
    $J(k, t_k) = \frac{m_{left}}{m}G_{left}+\frac{m_{right}}{m}G_{right}$
    $G_{left/right}$ : 왼쪽 / 오른쪽 서브셋의 불순도
    $m_{left/right}$ : 왼쪽 / 오른쪽 서브셋의 불순도

• 최대 깊이(max_depth)가 되거나 불순도를 줄이는 분할을 찾을 수 없을 때 멈추게 된다.

🔥6.5 계산 복잡도

• 예측을 위해서는 결정 트리의 루트 노드~리프 노드까지 탐색
  → 트리는 균형을 이루므로 결정 트리를 탐색하기 위해서는 $O(log_2(m))$개의 노드를 거쳐야 한다.

• 이때 각 노드의 하나의 특성값만 확인
  → 예측에 필요한 전체 복잡도는 특성과 무관하게 $O(log_2(m))$
  → 데이터가 많아져도 빠른 시간안에 가능!

• 각 노드에서 훈련 샘플의 모든 특성을 비교

  • 이때 max_features가 지정되어 있다면 이 값까지만
    → 훈련 복잡도 : $O(n \times mlog_2(m))$

🔥6.7 규제 매개변수

비파라미터 모델(nonparameter model) : 과대적합 ↑ 과소적합 ↓
훈련 데이터 제약 거의 X, 훈련되기 전에 파라미터 수 결정 X
→ 비파라미터 모델로 분류

파라미터 모델(parameter model) : 과대적합 ↓ 과소적합 ↑
파라미터 수 이미 결정 (자유도 제한)

결정 트리는 비파라미터 모델이기에 어느 정도 자유도를 제한할 필요가 있다. 이를 위해 규제 매개변수가 존재한다. 사이킷런에서는 기본값은 제한이 없다.

🔥DecisionTreeClassifier🔥

규제를 증가시키는 법
min_ : 매개변수 증가 max_: 매개변수 감소

class sklearn.tree.DecisionTreeClassifier(*, 
criterion='gini', splitter='best', max_depth=None,
min_samples_split=2, min_samples_leaf=1, 
min_weight_fraction_leaf=0.0, max_features=None, 
random_state=None, max_leaf_nodes=None, 
min_impurity_decrease=0.0, class_weight=None, ccp_alpha=0.0, 
monotonic_cst=None)[source]

위는 함수의 기본값이다. 자료는 사이킷런 공식 문서 참고

중요한 매개변수를 몇 개 살펴보자(여기 코드에 적힌 숫자는 모두 기본값이다)
criterion='gini' : {“gini”, “entropy”, “log_loss”}
: 분할의 품질을 측정, 즉 어떤 기준으로 데이터를 나누었을 때 그 분할이 얼마나 좋은지를 평가

min_samples_split=2:
: 분할되기 위해 노드가 가져 하는 최소 샘플 수

max_depth=None : {int}

• None : 분할의 깊이 제한이 없음
  • 각 리프 노드가 순수
  • 남은 샘플 수가 min_samples_split보다 적어 더 이상 나눌 수 없을 때까지 트리를 확장
  • 트리 성장을 제한하지 않기에 과대적합 가능성 ↑
• int : 해당 숫자까지 깊이 제한

min_samples_leaf=1:{int or float}
:리프 노드가 생성되기 위해 가지고 있어야 할 최소 샘플 수

정수값이면 해당 값을 최솟값으로,

If float, then min_samples_split is a fraction and ceil(min_samples_split * n_samples) are the minimum number of samples for each split.

실수값이면 전체 샘플 수(n_samples)에 대한 비율로 해석한다.
ceil(min_samples_split * n_samples) 값이 해당 분할을 진행하기 위해 필요한 최소 샘플 수가 되며, 여기서 ceil 함수는 올림 함수다.

min_weight_fraction_leaf=0.0
: min_samples_leaf=1와 같지만 가중치가 부여된 전체 샘플 수에서의 비율

직접 규제 해보기

from sklearn.datasets import make_moons

X_moons, y_moons = make_moons(n_samples=150,noise=0.2,random_state=42)

tree_clf1 = DecisionTreeClassifier(random_state=42)
tree_clf2 = DecisionTreeClassifier(min_samples_leaf=5, random_state=42)
tree_clf1.fit(X_moons, y_moons) # 규제 X
tree_clf2.fit(X_moons, y_moons) # 규제 O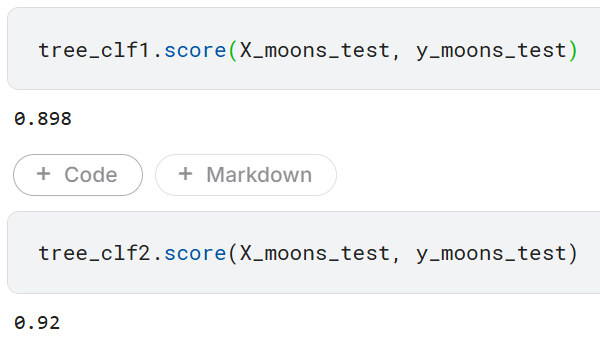

규제를 가하지 않은 tree_clf1의 정확도(0.898)가 규제를 가한 모델 tree_clf2 보다 정확도(0.92)가 낮게 측정되는 것을 볼 수 있다.

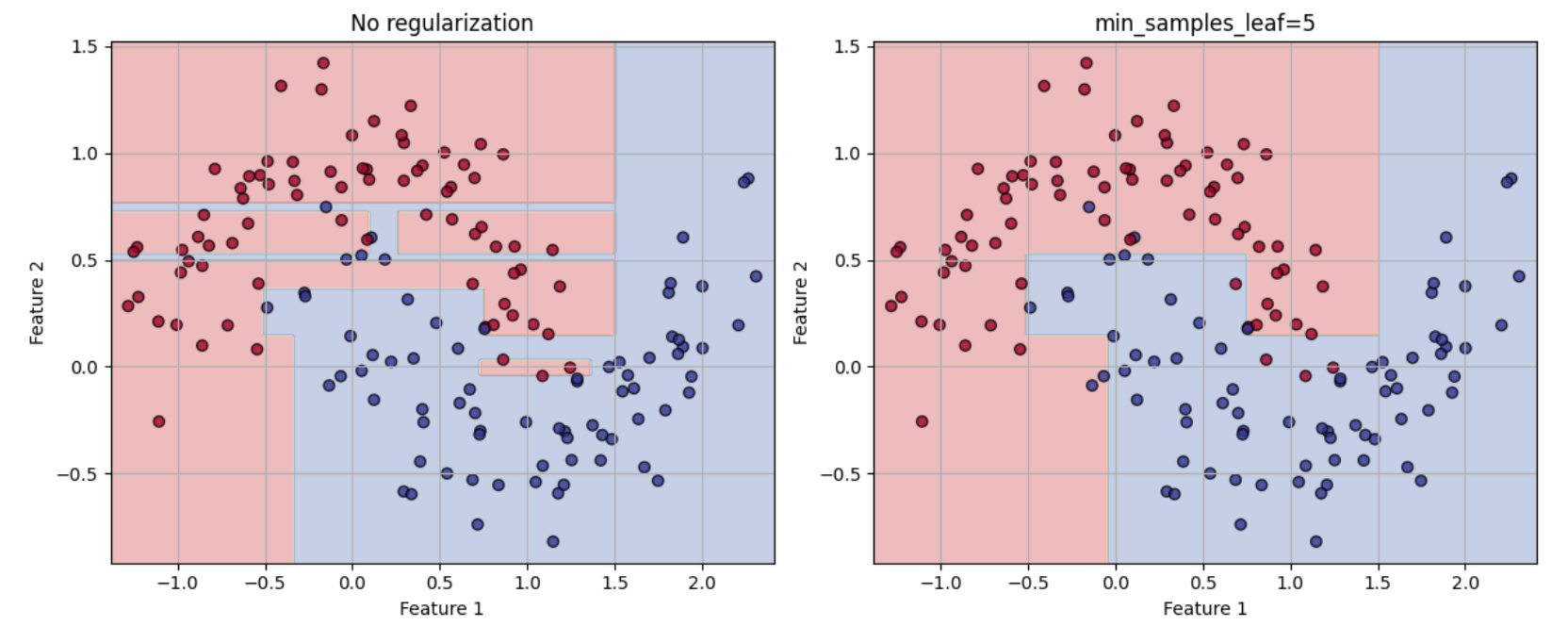
결정 경계를 실제로 그려보면 규제를 가한 모델이 더 일반화가 잘 되는 것을 볼 수 있다.

🔥6.8 회귀

sklearn의 DecisionTreeRegressor를 사용해서 2차 함수 형태의 데이터셋에서 max_depth=2 설정으로 회귀 트리를 만들어 보았다.

import numpy as np
from sklearn.tree import DecisionTreeRegressor

np.random.seed(42)
X_quad = np.random.rand(200, 1)
y_quad = X_quad**2+0.025*np.random.randn(200, 1)
tree_reg = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg.fit(X_quad, y_quad)

최소화해야 하는 CART 비용 함수

여기서

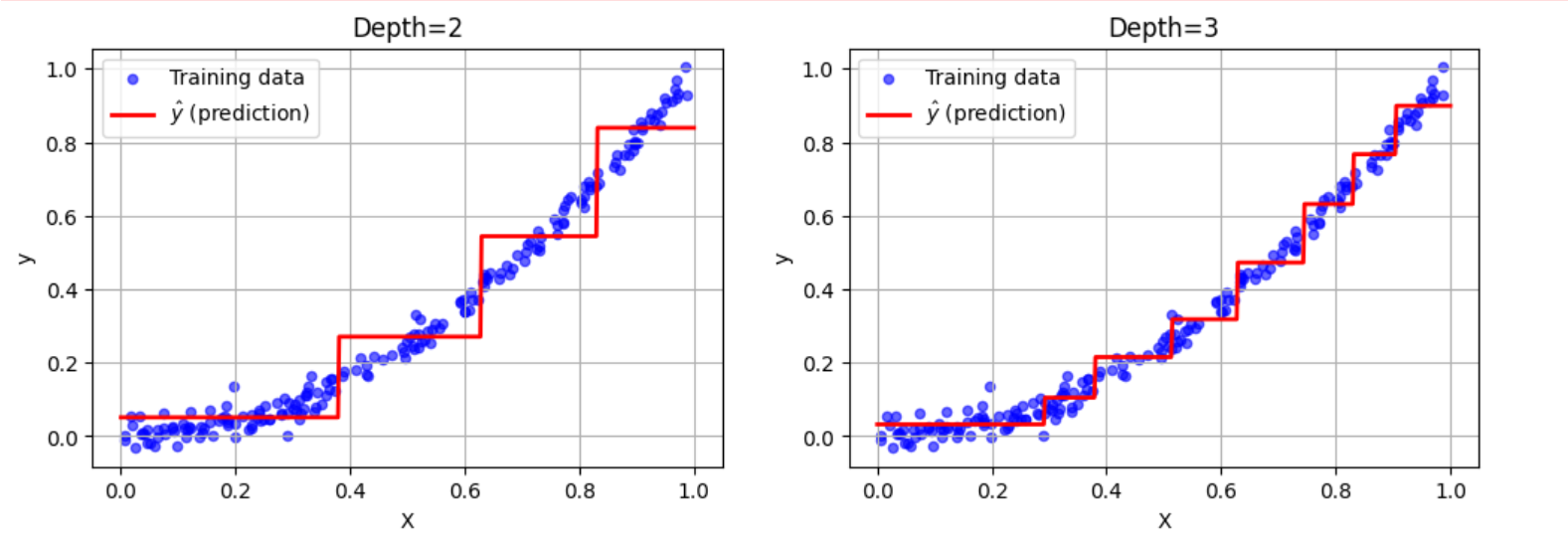
각 영역의 예측값은 항상 그 영역에 있는 타깃값의 평균이 된다. 알고리즘은 가능한 한 많은 샘플이 가까이 있도록 영역을 분할한다.

분류에서도 회귀 작업과 같이 결정 트리가 과대적합되기 쉽다는 것을 알 수 있다.

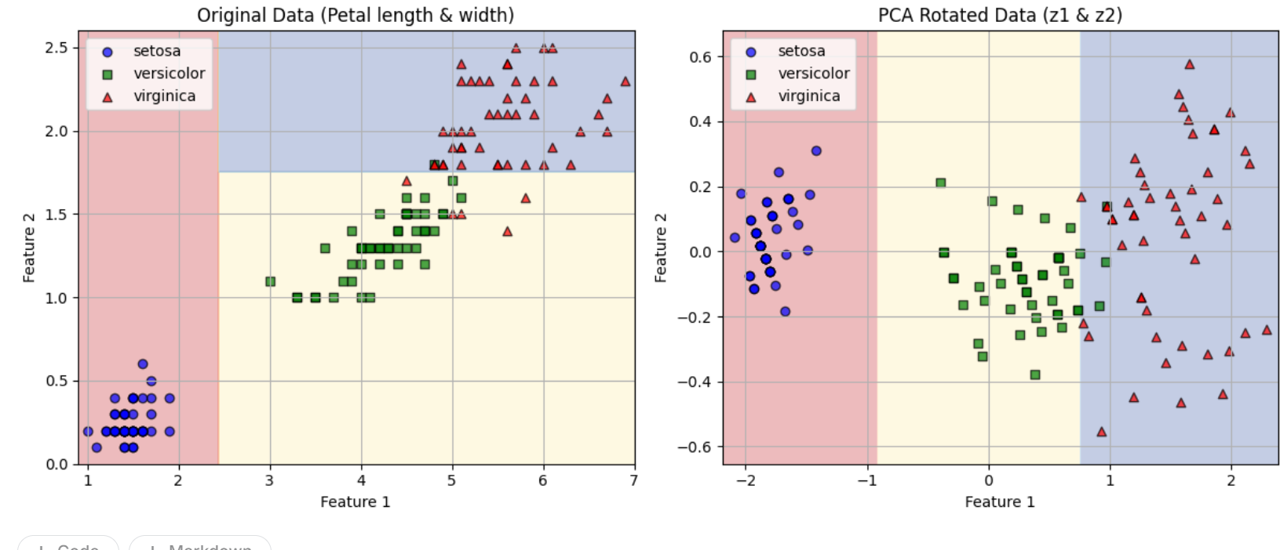
🔥6.9 축 방향에 대한 민감성

결정 트리는 계단 모양의 결정 경계를 만든다. (즉 모든 분할은 축에 수직이다.)
그래서 데이터 방향에 민감하다.

예를 들어 선형으로 구분될 수 있는 데이터셋을 보면,
만약 데이터를 45도 회전할 시, 트리의 경계가 구불구불해진다고 한다.
모두 완벽하게 학습하지만, 하나의 모델은 일반화가 잘 되지 않을 수 있다는 것이다...!

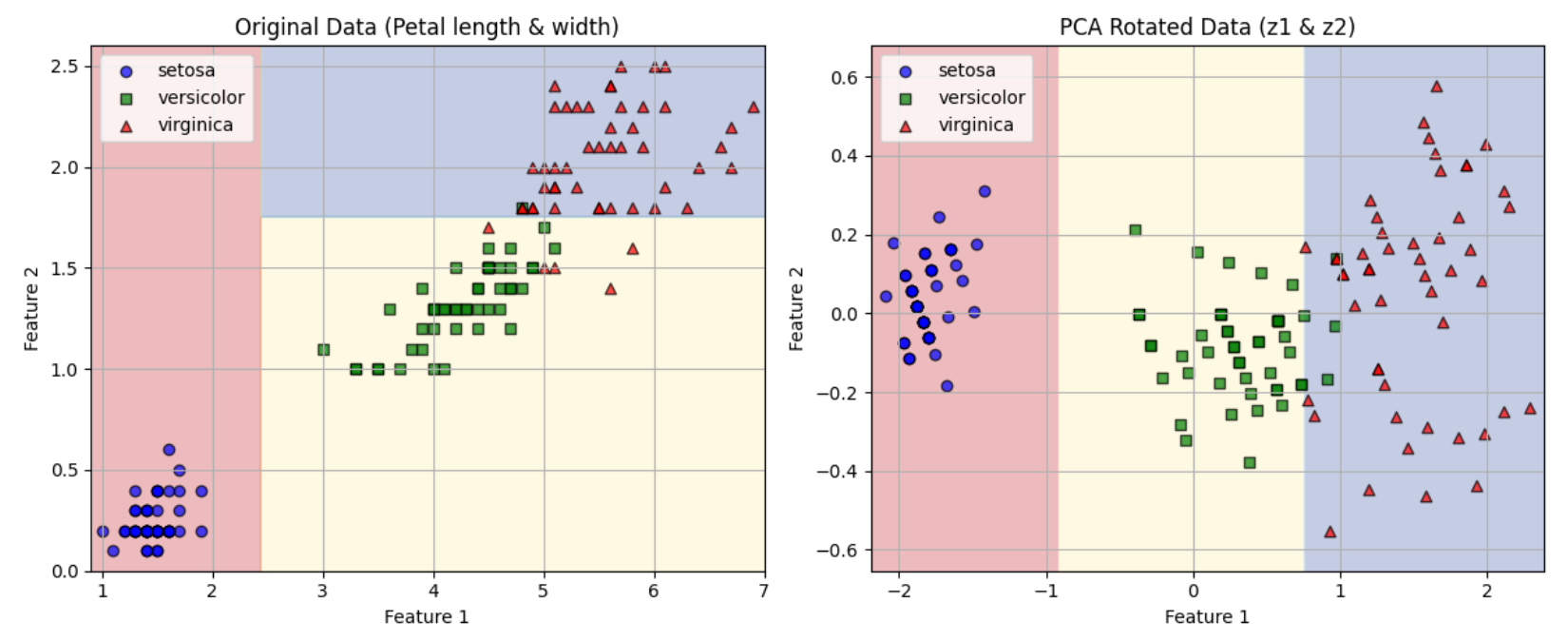
해결책 : PCA 변환 적용 (principal component analysis)

데이터를 회전하여 결정 트리를 더 쉽게 만든다

직접 해보기

from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

pca_pipeline = make_pipeline(StandardScaler(), PCA())
X_iris_rotated = pca_pipeline.fit_transform(X_iris)
tree_clf_pca = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf_pca.fit(X_iris_rotated, y_iris)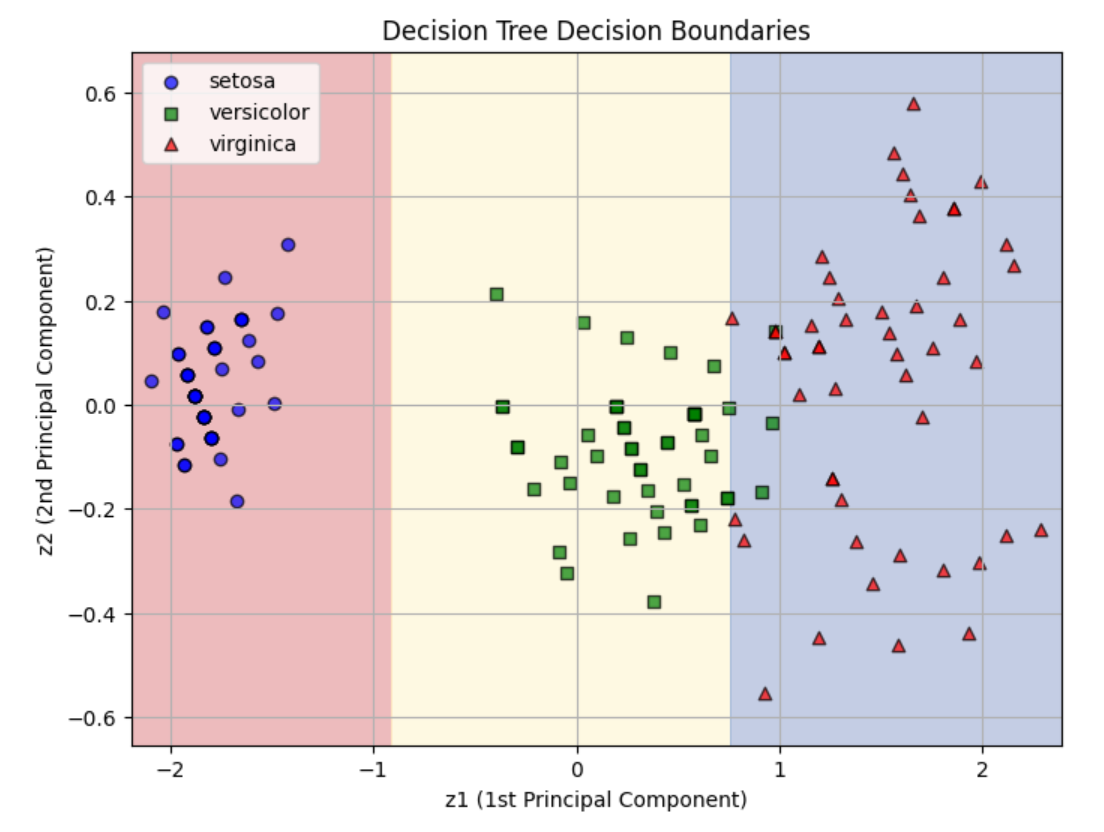

PCA 회전한 붓꽃 데이터셋에 대한 결정 트리의 경계

🔥6.10 결정 트리의 분산 문제

결정 트리의 주요 문제 : ❗분산이 상당히 크다는 것!❗

이는 하이퍼파라미터나 데이터를 조금만 변경해도 매우 다른 모델이 생성될 수 있다는 것을 뜻한다. 이 훈련 알고리즘은 확률적이므로 동일한 결정 트리를 재훈련하더라도 (random_state 매개변수를 설정하지 않는 한) 매우 다른 모델이 생성될 수 있다.

어떻게 해결하지? ❗여러 결정 트리❗를 이용하자!

여러 결정 트리의 예측을 평균하면 분산을 크게 줄일 수 있고, 이러한 결정 트리의 앙상블이 그 유명한 ❗랜덤 포레스트❗이다. 현재 사용 가능한 가장 강력한 종류의 모델이다.

참고 도서 : 핸즈온 머신러닝 3판