[250326수169H] 머신러닝 이론 (1) 지도학습

윤승호·2025년 3월 26일

비전공자 부트캠프 생존기

목록 보기

13/169

수학 지식이 중학교에 머물러 있다 보니 선형대수학 이론을 도무지 이해할 수가 없다. 시그마, 세타, 로그, 람다 등 태어나서 처음 들어본다. 오죽하면 수업 중간중간 나오는 파이썬 코드가 반가울 지경이다. 다 이해하고 넘어가기보다는 추후 실습을 하며 그때그때 참고하는 식으로 해야겠다. 계속하다 보면 답이 나오겠지!

학습시간 09:00~01:00(당일16H/누적169H)

1. 오늘 깨달은 것

사실 인풋이 너무 많아서 뭘 깨달을 여유조차 없었다. 굳이 몇 개 적자면 아래와 같다.

시그마가 뭔지 알게 됐다.

시그마는 1부터 특정 숫자까지 더하는 것

선형과 비선형의 차이에 대해 알게 됐다.

선형은 직선, 비선형은 곡선으로 나타난다.
선형은 중첩의 원리가 반드시 적용되어야 한다.

로지스틱 회귀모델은 비선형처럼 생겼는데 선형 모델이라는 것을 알게 됐다.

모델 자체는 선형이지만, 값을 분류하기 위해 시그모이드 함수를 활성화 함수로 사용하기 때문이다

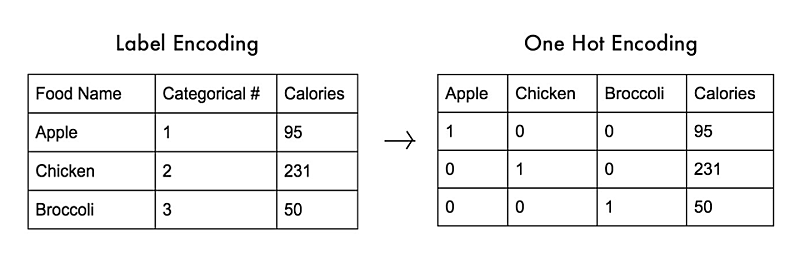
범주형 데이터를 전처리 할 수 있음을 알게 됐다.

원핫 인코딩을 통해 수치로 변환하면 모델에 적용 가능하다.

2. 머신러닝 이론

(1) 정의

일단, 인공지능은 규칙기반과 학습기반 두 종류가 있다.

규칙기반 = 사람이 알고리즘 설계(예전 방식)
학습기반 = 알고리즘 스스로 학습(최근 방식)

머신러닝은 학습기반 인공지능의 방법론이다. 보다 자세히 말하면, 데이터를 학습하고 새로운 데이터를 일반화 하여 명시적인 지시 없이 작업을 수행하는 알고리즘을 개발하는 학문이다.

즉, 데이터의 규칙(모델)을 찾는(학습하는) 기술이다.

모델 학습 = 데이터 규칙성을 찾기

머신러닝의 목표는 데이터를 기반으로 예측 모델을 만드는 것이다.

기계가 학습한다는 것은, 프로그램이 특정 작업(Task)를 하는 데 있어서 경험(Experience)을 통해 성능(Performance)을 향상시키는 과정이다.

(2) 머신러닝의 종류

A. Supervised Learning(지도학습)

정답(Y값, 라벨)이 있는 데이터
Regression(회귀) = 연속형 데이터 예측
Classification(분류) = 범주형 데이터 예측

B. Unsupervised Learning(비지도학습)

정답(Y값, 라벨)이 없는 데이터,
Clustering(군집화) = X간 그룹 파악
- 마케팅 고객 그룹화 등에 사용
Transformation(특성화) = X간 특성 파악
- 데이터 차원 축소 등에 사용

C. Semi-Supervised Learning(반지도학습)

정답(Y값, 라벨)이 부분적으로 있는 데이터

D. Reinforcement Learning(강화학습)

보상을 최대화하는 행동을 찾는 방법
- 알파고에 사용한 기술

(3) 모델은 어떻게 찾을까?

일단, 여기서 모델이란 예측값을 만드는 함수다. 제곱의 합(예측값과 실제값의 차이)을 최소화하는 방향으로 찾는다. cost가 낮은 hypothesis가 좋은 모델이다. 데이터에 맞는 모델은 여러 개 있을 수 있다.

hypothesis = 가설함수
cost = 평가지표

컴퓨터는 데이터로부터 모델을 구성하고 있는 Weight와 Bias를 학습한다.

weight = 함수의 계수
bias는 = 함수의 절편

(4) 컴퓨터가 어떻게 학습을?

A. 전반적인 순서
weight 초기값 랜덤 설정 → cost(예측값과 실제값이 차이) 측정 → 기울기를 파악 → cost를 줄이는 방향으로 weight 조정 → 반복

보통 기울기값이 weight값보다 크기 때문에 learning rate를 곱해서 조정한다.

기울기(Gradient) = 델타(cost, y) / 델타(weight, x)
weight = weight - learning rate * Gradient

B. 경사하강법(Gradient Descent Algorithm)

기울기를 계산하여 움직이는 방법이다.
기울기가 0인 지점이 최적의 weight다.

C. 교차검증(Cross Validation)
데이터를 여러 개의 그룹으로 나누어 검증하는 방법이다.

1단계: 훈련세트를 사용해 모델 학습
2단계: 검증세트를 사용해 모델 평가
3단계: 하이퍼 파라미터 조정
4단계: 테스트세트를 사용해 모델 평가

(5) 데이터 스케일링

데이터 스케일링은 데이터의 범위를 조정하는 것이다. 범위가 다르면 아래와 같은 문제가 발생할 수 있다.

모델의 성능이 떨어질 수 있다.
모델의 학습이 느려질 수 있다.
모델의 예측이 부정확해질 수 있다.

스케일링 종류는 아래와 같다.

표준화(Standardization)
정규화(Normalization)
차원 축소(Dimensionality Reduction)
로버스트 스케일링(Robust Scaling)

(6) 원핫 인코딩

범주형 데이터를 무작정 수치로 변환하면 제대로된 모델을 만들 수 없다. 예를 들어, 혈액형을 수치로 변환하면 크고 작다의 개념이 생겨버린다. 그래서 원핫 인코딩(One-Hot Encoding)을 해준다. 범주가 100개면 100개의 컬럼을 만들어야 한다.

(7) 모델 평가 지표

정확도(Accuracy)
오차행렬(Confusion Matrix)
정밀도(Precision)
재현율(Recall)
F1 스코어(F1 Score)
ROC AUC곡선(ROC AUC Curve)

3. 회귀 모델 종류

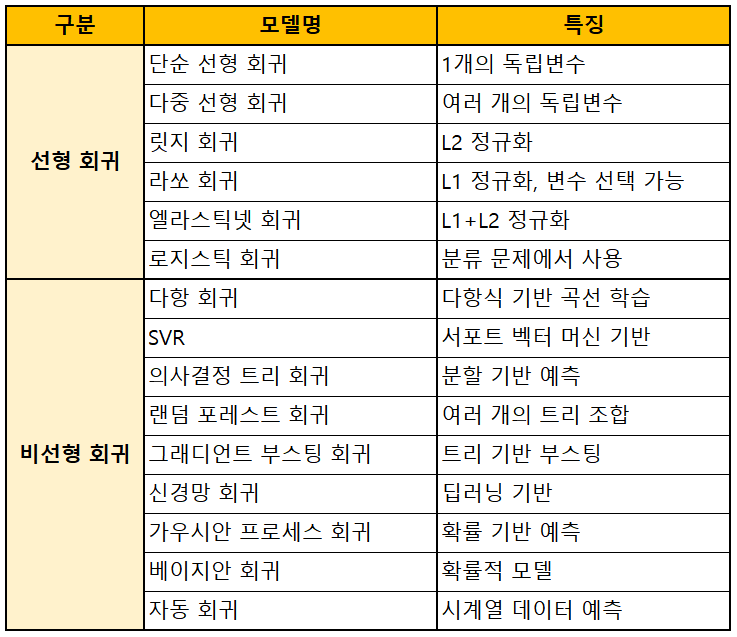
(1) 선형 회귀 모델

출력값이 직선으로 표현되는 회귀 모델.

선형 회귀 (Simple Linear Regression): 하나의 독립변수(𝑥)를 이용하여 종속변수(𝑦)를 예측하는 가장 기본적인 회귀 모델.
다중 선형 회귀 (Multiple Linear Regression): 여러 개의 독립변수(𝑥₁, 𝑥₂, ...)를 이용하여 종속변수(𝑦)를 예측.
릿지 회귀 (Ridge Regression): L2 정규화를 추가하여 모델의 가중치 크기를 줄여 과적합을 방지.
라쏘 회귀 (Lasso Regression): L1 정규화를 추가하여 일부 가중치를 0으로 만들어 변수 선택 효과를 가짐.
엘라스틱넷 회귀 (Elastic Net Regression): 릿지와 라쏘의 조합으로, 두 정규화 효과를 모두 적용.
로지스틱 회귀 (Logistic Regression): 분류 문제에서 사용되지만, 입력 변수로 선형 조합을 사용하기 때문에 선형 모델로 간주됨. 활성화 함수로 시그모이드 함수를 사용하면 확률 값(0~1)을 출력 가능.
다항 로지스틱 회귀 (Multinomial Logistic Regression): 3개 이상의 클래스를 예측.

★ 로지스틱 회귀에 사용 가능한 활성화 함수는 시그모이드, 하드 시그모이드, 탄젠트 하이퍼볼릭, probit 함수 등이 있다.

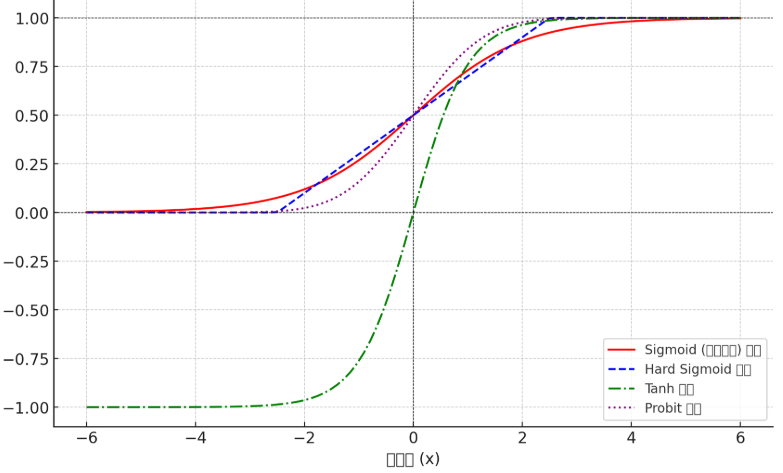
시그모이드(Sigmoid) 함수: 로지스틱 회귀에서 가장 많이 사용되는 함수로, 0과 1 사이의 값을 출력한다.
하드 시그모이드(Hard Sigmoid) 함수: 시그모이드 함수에서 복잡도를 낮추고 연산을 더 쉽게 만든 대체 함수다
탄젠트 하이퍼볼릭(Tanh) 함수: -1과 1 사이의 값을 출력하며, 시그모이드보다 중심이 0에 가까워 학습이 빠를 수 있다.
Probit 함수: 정규 누적 분포 함수(CDF)로 확률을 모델링할 때 사용된다.

(2) 비선형 회귀 모델

출력값이 곡선으로 표현되는 회귀 모델.

다항 회귀 (Polynomial Regression): 입력 변수의 거듭제곱(𝑥², 𝑥³ 등)을 포함하여 곡선을 학습하는 회귀 모델. 입력 변수는 선형이지만, 변형을 통해 비선형 관계를 학습.
일반화 가법 모델 (Generalized Additive Models, GAMs): 여러 개의 비선형 함수를 조합하여 예측.
서포트 벡터 회귀 (Support Vector Regression, SVR): 서포트 벡터 머신(SVM)을 회귀 문제에 적용. 비선형 커널을 사용하여 복잡한 패턴을 학습 가능.
의사결정 회귀 트리 (Decision Tree Regression): 데이터를 여러 개의 구간으로 나누고 각 구간별 평균 값을 예측. 선형 모델과 달리, 계단식 함수 형태를 띔.
랜덤 포레스트 회귀 (Random Forest Regression): 여러 개의 의사결정 트리를 조합하여 예측 성능을 향상.
그래디언트 부스팅 회귀 (Gradient Boosting Regression): 여러 개의 약한 의사결정 트리를 순차적으로 학습하여 성능을 개선. XGBoost, LightGBM, CatBoost 등 여러 가지 변형이 존재.
신경망 회귀 (Neural Network Regression): 인공 신경망(ANN, DNN, CNN, RNN 등)을 활용한 복잡한 비선형 회귀 모델.
가우시안 프로세스 회귀 (Gaussian Process Regression, GPR): 확률적 방법을 사용하여 예측값과 불확실성을 함께 추정.
베이지안 회귀 (Bayesian Regression): 베이지안 확률 모델을 기반으로 한 회귀 모델. 베이지안 릿지 회귀, 베이지안 정규 회귀 등이 존재.
자동 회귀 (Auto Regression, AR): 시계열 데이터에서 과거 값을 이용하여 미래 값을 예측.

4. 선형과 비선형의 차이점

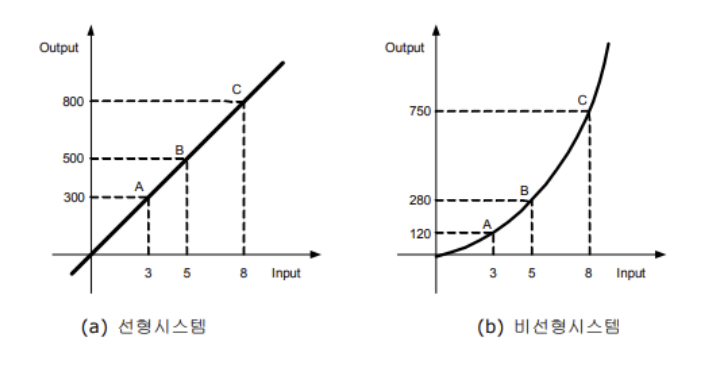
(1) 선형 모델 특징

변수(특징, 입력값)와 출력값 사이의 관계가 직선 또는 평면으로 나타난다.
수식이 일차식(덧셈과 곱셈만 포함)으로 구성된다.
입력값이 변할 때 일정한 비율로 결과값이 변한다.
예) 다중 선형 회귀

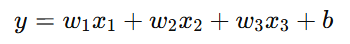
(2) 비선형 모델 특징

변수와 출력값 사이의 관계가 곡선 또는 복잡한 형태로 나타난다.
수식에 제곱, 루트, 로그, 지수, 곱셈 연산 등이 포함될 수 있다.
입력값이 변할 때 일정한 비율이 아니라 비례하지 않는 변화를 보인다.
예) 다항 회귀

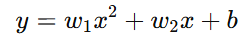
(3) 선형과 중첩의 원리

A. 중첩의 원리 설명

어떤 수식을 선형이라 부르기 위해서는 반드시 중첩의 원리(superposition principle)가 적용되어야 한다.

예를 들어, 직선의 방정식 y=ax를 고려해보자.

서로 다른 입력값인 x1과 x2를 함수에 대입했을 때 구해지는 함수값은 각각 ax1과 ax2이다.

이 때, x1+x2의 함수값은 a(x1+x2)로 x1과 x2의 함수값을 각각 구하고 더해준 ax1+ax2값과 동일하다.

너무나 당연한 말처럼 보이지만, 이것이 대단히 중요하고 유용한 중첩의 원리이다.

비선형문제는 이런 논리가 통하지 않게된다. 결과값이 입력값에 전혀 상관없어 보일만큼 전혀 예측이 불가능한 해가 나오기도 하는 것이 비선형 문제인 것이다.

(출처: https://sdolnote.tistory.com/entry/Linearity)

B. 중첩의 원리 예시

★ "더하는 순서와 방식"에 상관없이 결과가 같으면 선형이다!

예를 들어, 시급이 10,000원이라 가정해보자.
2시간 근무 → 10,000 × 2 = 20,000원
4시간 근무 → 10,000 × 4 = 40,000원

그럼 2시간 + 4시간 일하면?
곱하고 더하기 → 20,000 + 40,000 = 60,000원
더하고 곱하기 → 10,000 × (2+4) = 60,000원

= 결과가 같다.

★ "더하는 순서와 방식"에 따라 결과가 바뀌면 비선형이다!

이번엔 2시간 이상부터 시급이 2배가 된다고 가정해보자.
2시간 근무 → 10,000 × 2 = 20,000원
4시간 근무 → 20,000 × 4 = 80,000원

그럼 2시간 + 4시간 일하면?
곱하고 더하기 → 20,000 + 80,000 = 100,000원
더하고 곱하기 → 20,000 × (2+4) = 120,000원

= 결과가 다르다.

(4) 모델 모습 예시

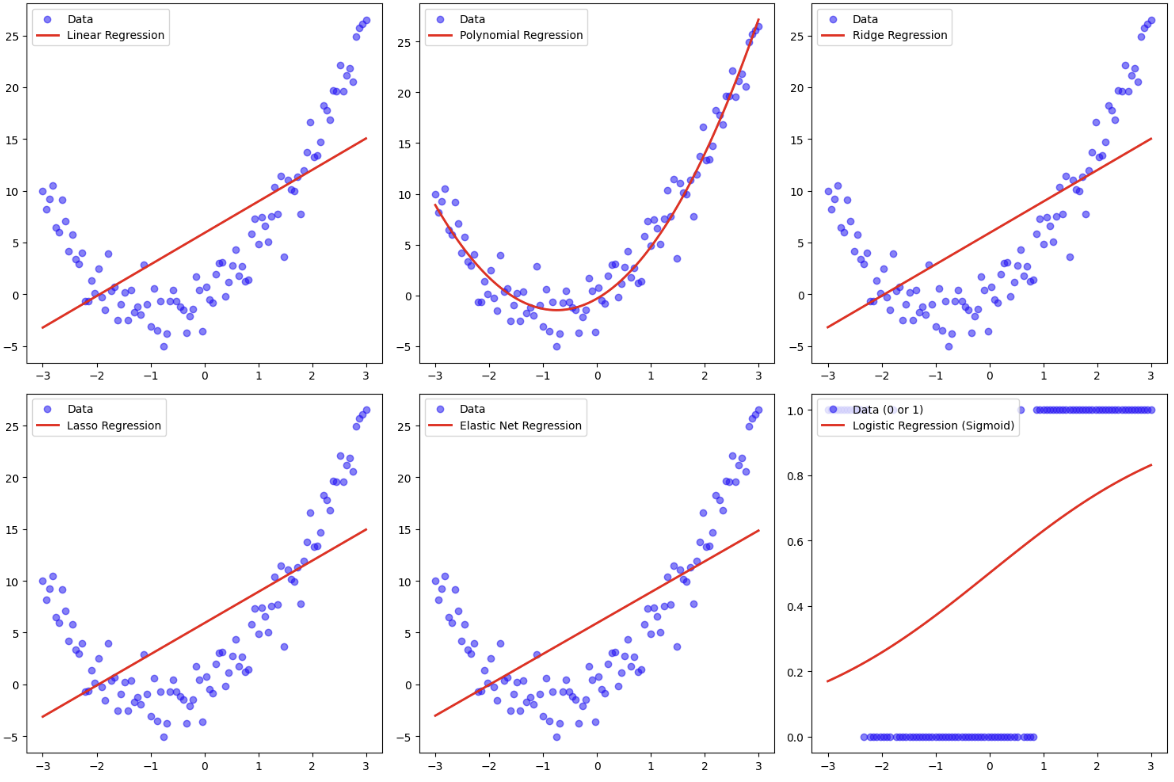
GPT 도움을 받아 아래 코드를 사용했다.

from sklearn.linear_model import Ridge, Lasso, ElasticNet, LogisticRegression

# 데이터 생성 (비선형 형태)
np.random.seed(42)
X = np.linspace(-3, 3, 100).reshape(-1, 1)
y = 2 * X**2 + 3 * X + np.random.randn(100, 1) * 2  # 2차 함수 + 노이즈

# 로지스틱 회귀를 위한 이진 분류 데이터 생성
y_binary = (y > np.median(y)).astype(int).ravel()  # 중앙값 기준으로 0과 1로 분류

# 모델 학습
linear_model = LinearRegression().fit(X, y)  # 다중선형회귀
poly_features = PolynomialFeatures(degree=2).fit_transform(X)
poly_model = LinearRegression().fit(poly_features, y)  # 다항회귀
ridge_model = Ridge(alpha=1).fit(X, y)  # 릿지 회귀
lasso_model = Lasso(alpha=0.1).fit(X, y)  # 라쏘 회귀
elasticnet_model = ElasticNet(alpha=0.1, l1_ratio=0.5).fit(X, y)  # 엘라스틱넷 회귀
logistic_model = LogisticRegression().fit(X, y_binary)  # 로지스틱 회귀

# 예측값 계산
y_pred_linear = linear_model.predict(X)
y_pred_poly = poly_model.predict(poly_features)
y_pred_ridge = ridge_model.predict(X)
y_pred_lasso = lasso_model.predict(X)
y_pred_elasticnet = elasticnet_model.predict(X)
y_pred_logistic = logistic_model.predict(X)

# 그래프 그리기
fig, axes = plt.subplots(2, 3, figsize=(15, 10))

# 다중선형회귀
axes[0, 0].scatter(X, y, color='blue', alpha=0.5, label="Data")
axes[0, 0].plot(X, y_pred_linear, color='red', linewidth=2, label="Linear Regression")
axes[0, 0].legend()

# 다항회귀
axes[0, 1].scatter(X, y, color='blue', alpha=0.5, label="Data")
axes[0, 1].plot(X, y_pred_poly, color='red', linewidth=2, label="Polynomial Regression")
axes[0, 1].legend()

# 릿지 회귀
axes[0, 2].scatter(X, y, color='blue', alpha=0.5, label="Data")
axes[0, 2].plot(X, y_pred_ridge, color='red', linewidth=2, label="Ridge Regression")
axes[0, 2].legend()

# 라쏘 회귀
axes[1, 0].scatter(X, y, color='blue', alpha=0.5, label="Data")
axes[1, 0].plot(X, y_pred_lasso, color='red', linewidth=2, label="Lasso Regression")
axes[1, 0].legend()

# 엘라스틱넷 회귀
axes[1, 1].scatter(X, y, color='blue', alpha=0.5, label="Data")
axes[1, 1].plot(X, y_pred_elasticnet, color='red', linewidth=2, label="Elastic Net Regression")
axes[1, 1].legend()

# 로지스틱 회귀 (시그모이드 곡선)
X_range = np.linspace(-3, 3, 100).reshape(-1, 1)
y_prob = logistic_model.predict_proba(X_range)[:, 1]  # 클래스 1에 대한 확률

axes[1, 2].scatter(X, y_binary, color='blue', alpha=0.5, label="Data (0 or 1)")
axes[1, 2].plot(X_range, y_prob, color='red', linewidth=2, label="Logistic Regression (Sigmoid)")
axes[1, 2].legend()

plt.tight_layout()
plt.show()

윤승호

나는 AI 엔지니어가 된다.

이전 포스트

[250325화153H] 호텔 데이터 전처리 (3)

다음 포스트