지옥 같은 하루. 아무래도 이 포스팅은 두고두고 찾아볼 것 같다. 제목에 별도 달았음.

학습시간 09:00~01:00(당일16H/누적185H)

◆ 오늘 깨달은 것

무엇을 깨달았는지 기억나지 않을 때도 있다는 것을 깨달았다.

◆ sklearn

# 데이터 분할 및 샘플링
from sklearn.model_selection import train_test_split, cross_val_score, KFold, GridSearchCV

# 전처리 (스케일링, 인코딩, 변환 등)
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler, OneHotEncoder, LabelEncoder, PolynomialFeatures

# 회귀 모델
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet

# 분류 모델
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeClassifier

# 회귀 평가 지표
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score

# 분류 평가 지표
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, confusion_matrix, classification_report

# PCA (차원 축소)
from sklearn.decomposition import PCA

# K-Means (군집화)
from sklearn.cluster import KMeans

◆ 지도 학습

→ 관례적으로 X와 W는 대문자, y와 b는 소문자를 사용
→ 대문자 X는 행렬을 의미하고 소문자 y는 벡터를 나타내기 때문
→ 머신러닝에서는 X(특징)와 y(타겟) 표기법이 전통적인 규칙
→ X는 입력 데이터(특징 행렬), W는 가중치(Weight), b는 절편(Bias), y는 보통 타겟 값 또는 정답

1. 데이터 로드 및 확인

df = pd.read_csv('data/boston.csv')
df.head()

2. 원핫인코딩(필요시)

df_encoded = pd.get_dummies(df, columns=['A']).replace({False:0, True:1})

→ A열을 0과 1로 이루어진 열로 변환
→ 원핫인코딩 시 df_encoded로 저장

X = df_encoded.drop(['A'], axis=1)
y = df_encoded['A']

3. 변수(X, y) 선언

방법1. y열이 중간에 있을 경우

X = df.drop(['A'], axis=1)
y = df.['A']

방법2. y열이 맨 오른쪽일 경우

X = df[df.columns[:-1]]
y = df[df.columns[-1]]

→ X는 독립변수(문제), y는 종속변수(정답)

4. 스케일링(표준화)

from sklearn.preprocessing import StandardScaler
ss = StandardScaler() # 표준화 스케일링 변수 선언
X_scaled = ss.fit_transform(X) # 스케일된 X

→ 데이터를 일정한 범위로 맞추는 것

5. 데이터 스플릿

X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2)

→ 스케일링한 문제(X)와 정답(y)를 기반으로 스플릿
→ train은 학습용, test는 평가용
→ X는 문제, y는 정답
→ test 비율을 20%로 하겠다는 뜻
→ 스플릿 후 차원 확인

X_train.shape, X_test.shape, y_train.shape, y_test.shape

6. 다항식 변환(필요시)

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)

→ degree는 방정식의 차수
→ include_bias는 상수항 포함 여부
→ ★다항식 변환 시 다음 단계에 X_train 대신 X_train_poly를 넣어야 함
→ 차수 확인하고 싶으면 feature_names = poly.get_feature_names_out() 코드 입력

7. 모델 호출

(1) 선형 회귀

from sklearn.linear_model import LinearRegression
lr = LinearRegression()

(2) 로지스틱 회귀

from sklearn.linear_model import LogisticRegression
logr = LogisticRegression(C=10, random_state=20)

→ C는 하이퍼파라미터(정규화 강도, 값 클수록 자유로움)
→ random_state는 랜덤성 제어(항상 같은 데이터 사용)

logr.classes_
for i in logr.predict_proba(X_test)[:10]:
    print(i, np.argmax(i))
pred_test[:10]

→ 이건 뭔지 잘 모르겠음

(3) 확률적 경사하강법(학습 동시 진행)

sc = SGDClassifier(loss='log_loss', max_iter=100, random_state=20)
sc.fit(train_x, train_y)
sc.n_iter_

→ SGD는 Stochastic Gradient Descent 임
→ 배치 경사하강법보다 쉽고 간편하며 빠름
→ loss='logloss'는 로지스틱 회귀를 위한 손실함수
→ loss='hinge'는 힌지 손실 함수(SVM처럼 동작)
→ loss='perceptron'퍼셉트론 손실 함수
→ max_iter는 최대 반복 횟수
→ sc.n_iter은 몇 번 진행했는지 호출

8. 모델 학습

모델변수명.fit(X_train, y_train)

→ 모델에게 문제와 정답 제공
→ 모델이 X와 y사이의 관계를 배움

# 모델 기울기와 절편 확인
모델변수명.coef_, lr.intercept_

→ 반드시 확인할 필요는 없음

9. 정답 예측

pred_train = lr.predict(X_train) # 정답을 아는 문제 예측
pred_test = lr.predict(X_test) # 정답을 모르는 문제 예측

→ y값은 정답이기 때문에 필요가 없음

10. 비교 그래프 생성(필요시)

# DataFrame 생성
df_train = pd.DataFrame({'X': X_train.values.flatten(), 'y_true': y_train, 'y_pred': pred_train})
df_train = df_train.sort_values('X')

# 1행 2열 서브플롯 생성
fig, axes = plt.subplots(1, 2, figsize=(12, 5))  

# 왼쪽 그래프: 원본 데이터 산점도
axes[0].scatter(X, y, color='b')
axes[0].set_title('Original Data')

# 오른쪽 그래프: 다항 회귀 결과
axes[1].scatter(X_train, y_train, color='b')
axes[1].plot(df_train['X'], df_train['y_pred'], color='r')
axes[1].set_title('Polynomial Regression')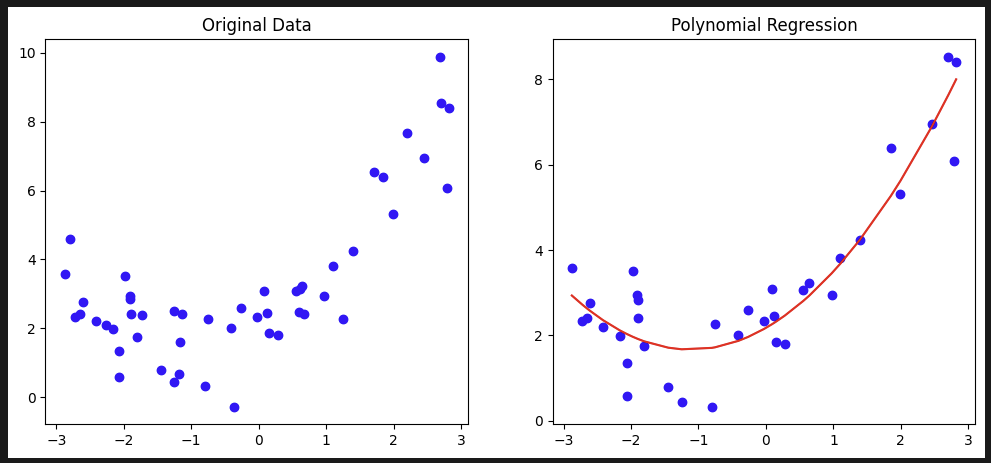

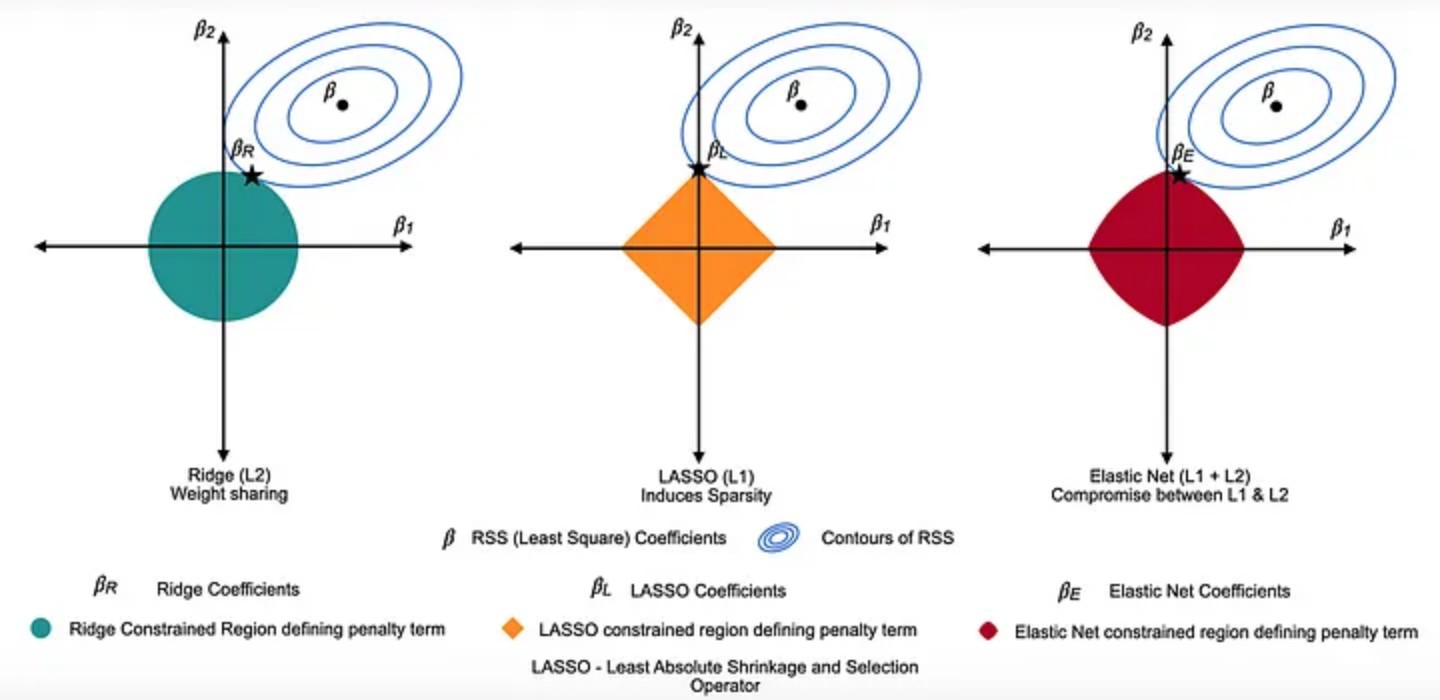
11. Regularization(규제, 정규화)

(1) ridge

''' ridge 정규화 '''
from sklearn.linear_model import Ridge

# 1. 모델 선언
ridge = Ridge(alpha=0.001, max_iter=100, random_state=20)
ridge.get_params()

# 2. 모델 학습
ridge.fit(X_train_poly, y_train)

# 3. 예측
pred_train = ridge.predict(X_train_poly)
pred_test = ridge.predict(X_test_poly)

# 4. DataFrame 생성
df_train = X_train.copy()
df_train['pred_train'] = pred_train
df_train = df_train.sort_values('X')

# 5. 데이터 시각화
plt.scatter(X_train, y_train, color='blue')
plt.plot(df_train['X'], df_train['pred_train'], color='red')
plt.show()

(2) lasso

''' lasso 정규화 '''
from sklearn.linear_model import Lasso

# 1. 모델 선언
lasso = Lasso(alpha=0.001, max_iter=100, random_state=20)
lasso.get_params()

# 2. 모델 학습
lasso.fit(X_train_poly, y_train)

# 3. 예측
pred_train = lasso.predict(X_train_poly)
pred_test = lasso.predict(X_test_poly)

# 4. DataFrame 생성
df_train = X_train.copy()
df_train['pred_train'] = pred_train
df_train = df_train.sort_values('X')

# 5. 데이터 시각화
plt.scatter(X_train, y_train, color='blue')
plt.plot(df_train['X'], df_train['pred_train'], color='red')
plt.show()

(3) elasticnet

''' elasticnet 정규화 '''
from sklearn.linear_model import ElasticNet

# 1. 모델 선언
en = ElasticNet(alpha=0.001, l1_ratio=0.5, max_iter=100, random_state=20)

# 2. 모델 파라미터 확인
en.get_params()

# 3. 모델 학습
en.fit(X_train_poly, y_train)

# 4. 예측
pred_train = en.predict(X_train_poly)
pred_test = en.predict(X_test_poly)

# 5. DataFrame 생성
df_train = X_train.copy()
df_train['pred_train'] = pred_train
df_train = df_train.sort_values('X')

# 6. 데이터 시각화
plt.scatter(X_train, y_train, color='blue')
plt.plot(df_train['X'], df_train['pred_train'], color='red')
plt.show()

12. 성능 평가

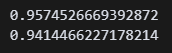
(1) 스코어

print(lr.score(X_train, y_train))
print(lr.score(X_test, y_test))

→ 학습용 데이터와 평가용 데이터 비교
→ 스코어가 1에 가까우면 좋은 모델

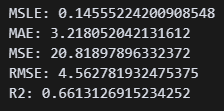
(2) 평가지표

# 평가지표 호출
from sklearn.metrics import (
    mean_squared_error,
    mean_absolute_error,
    mean_squared_log_error,
    root_mean_squared_error,
    r2_score)
    
# 평가 함수 설정
def evaluate(test, pred):
    print(f"MSLE: {mean_squared_log_error(test, pred)}")
    print(f"MAE: {mean_absolute_error(test, pred)}")
    print(f"MSE: {mean_squared_error(test, pred)}")
    print(f"RMSE: {root_mean_squared_error(test, pred)}")
    print(f"R2: {r2_score(test, pred)}")  
    
# 모델 평가
evaluate(y_test, pred_test)

→ 예측한 정답(pred_test)와 실제 정답(y_test)을 확인

(3) 오차행렬

# 매트릭 호출
from sklearn.metrics import (
    accuracy_score, # 정확도
    precision_score, # 정밀도
    recall_score, # 재현율
    f1_score, # F1 점수
    confusion_matrix, # 오차행렬
    classification_report) # 분류 보고서
    
# 매트릭 출력(이진 클래스)
print("Accuracy:", accuracy_score(y_test, pred_test))
print("Precision:", precision_score(y_test, pred_test))
print("Recall:", recall_score(y_test, pred_test))
print("F1 Score:", f1_score(y_test, pred_test))
print("Confusion Matrix:\n", confusion_matrix(y_test, pred_test))
print("Classification Report:\n", classification_report(y_test, pred_test))

# 매트릭 출력(다중 클래스)
print("Accuracy:", accuracy_score(y_test, pred_test))
print("Precision:", precision_score(y_test, pred_test, average='weighted'))
print("Recall:", recall_score(y_test, pred_test, average='weighted'))
print("F1 Score:", f1_score(y_test, pred_test, average='weighted'))
print("Confusion Matrix:\n", confusion_matrix(y_test, pred_test))
print("Classification Report:\n", classification_report(y_test, pred_test))

# 오차행렬 시각화
cm = confusion_matrix(y_test, pred_test)
sns.heatmap(cm, annot=True, cmap='Blues')
plt.xlabel('Actual')
plt.ylabel('Predicted')
plt.show()

◆ 그 외 스킬

이해하지 못했으므로 일단 저장

1. 배치 경사하강법(Batch Gradient Descent)

fit 함수로 학습을 제대로 못할 경우 경사하강법 사용

장점: 모든 데이터를 한 번에 처리하여 정확한 기울기를 계산하므로 수렴이 안정적이고 정확

단점: 데이터셋이 클 경우 메모리 소비가 많고 계산 속도가 느려질 수 있음.

데이터가 많으면 SGD(Stochastic Gradient Descent, 확률적 경사하강법) 사용하는 것이 좋음

# Weight 랜덤 초기화 (X의 열 수에 맞게)
W = np.random.randn(X.shape[1])  
# Bias 랜덤 초기화
b = np.random.randn(1)  

learning_rate = 0.1  # 학습률
epsilon = 1.1  # 오차 허용 범위 (쓰레쉬 홀드)
max_epochs = 500  # 최대 반복 횟수
y_preds = [] # 예측값 저장 리스트

for epoch in range(max_epochs):
    # 예측값 계산
    y_pred = np.dot(X, W) + b
    # 예측값 저장
    y_preds.append(y_pred)
    # MSE (Mean Squared Error) 계산
    mse = np.mean((y_pred - y) ** 2)
    
    # MSE가 epsilon 이하로 내려가면 종료
    if mse <= epsilon:
        print(f"MSE reaches below {epsilon}")
        print(f"MSE: {mse} | epoch: {epoch}")
        break

    # 기울기 계산 (w_gradient)
    w_gradient = (2 / len(X)) * np.dot(X.T, (y_pred - y))
    
    # 절편 계산 (b_gradient)
    b_gradient = (2 / len(X)) * np.sum(y_pred - y)
    
    # Weight와 Bias 업데이트
    W = W - learning_rate * w_gradient
    b = b - learning_rate * b_gradient
    
    # 각 epoch마다 MSE 출력
    print(f"MSE: {mse} | epoch: {epoch}")

2. 그리드 서치

''' Grid Search(그리드 서치)찾는 방법 '''
# 어떤 하이퍼 파라미터가 가장 좋은 성능을 보이는지 찾는 방법
from sklearn.model_selection import GridSearchCV # cross validation을 하는 방법
from sklearn.svm import SVR # 소프트 벡터 머신
from sklearn.datasets import load_diabetes
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split # train_test_split 추가

# 1. 데이터 불러오기
dia = load_diabetes()
X = dia.data
y = dia.target

# 2. 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=20)

# 3. 표준화
ss = StandardScaler()
X_scaled = ss.fit_transform(X_train) # X_train을 표준화해야 함

# 4. SVR 모델 선언
svr = SVR()

# 1. 하이퍼 파라미터 설정
param_grid = {"kernel": ["linear", "poly", "rbf"],
              "gamma": ["scale", "auto"],
              "C": [0.001, 0.01, 0.1, 1, 10]}

# 2. 모델 선언
gridcv = GridSearchCV(estimator=svr, param_grid=param_grid, cv=5, scoring='r2', verbose=10)

# 5. 모델 학습
gridcv.fit(X_scaled, y_train) # 모델 학습 추가

# 6. 결과 확인
cv_results = pd.DataFrame(gridcv.cv_results_)
print(cv_results) # 결과 출력 추가

print(gridcv.best_params_) # 최적의 파라미터 출력 추가

3. 차원축소

''' 차원축소 방법 '''
# 1. 데이터셋 불러오기
wine = pd.read_csv('data/wine.csv')

# 2. 피쳐, 타겟 분리
X = wine[wine.columns[:-1]]
y = wine[wine.columns[-1]]

# 3. 피쳐에 대한 스케일링
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
X_scaled = ss.fit_transform(X)

# 4. 피쳐에 대해 차원축소 진행(2차원)
from sklearn.decomposition import PCA
pca = PCA(n_components=2) # 2차원으로 줄이겠다는 뜻
X_pca = pca.fit_transform(X_scaled)

# 5. 축소된 각 컬럼에 대한 중요도 계산
explained_variance = pca.explained_variance_ratio_
# np.cumsum(explained_variance) 하면 누적된 중요도 나옴
# 0.3619, 0.5540 나옴, 전체의 
# 36% 정도 중요도를 가지고 있고, 전체의 55% 정도 중요도를 가지고 있다는 뜻
wine['Customer_Segment'].value_counts()

# 6. 데이터 시각화 방법 1
wine_class = [1, 2, 3]
for cls in wine_class:
    plt.scatter(X_pca[y==cls, 0], X_pca[y==cls, 1], label=str(cls))
plt.legend()
plt.show()

# 6. 데이터 시각화 방법 2
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
plt.legend()
plt.show()

4. 샘플링

(1) 데이터 생성 및 불균형 확인

from sklearn.datasets import make_classification
from collections import Counter
import matplotlib.pyplot as plt

# 불균형 데이터 생성
x, y = make_classification(
    n_classes=2,  # 클래스 개수 (이진 분류)
    weights=[0.1, 0.9],  # 클래스 불균형 (10:90 비율)
    class_sep=3,  # 클래스 분리 정도
    n_features=20,  # 특성 개수
    n_samples=1000,  # 샘플 개수
    random_state=10  # 랜덤 시드
)

# 클래스 비율 확인
print(Counter(y))  # {0: 100, 1: 900} (불균형 확인)


## 1000개의 샘플 중 클래스 0은 100개, 클래스 1은 900개로 불균형함.

(2) 언더샘플링 (RandomUnderSampler)

from imblearn.under_sampling import RandomUnderSampler

# 랜덤 언더샘플링 수행
rus = RandomUnderSampler(sampling_strategy='auto')
x_rus, y_rus = rus.fit_resample(x, y)

# 샘플링 결과 확인
print(Counter(y_rus))  # {0: 100, 1: 100} (균형 맞춰짐)

# 시각화
plt.scatter(x_rus[:, 0], x_rus[:, 1], c=y_rus)
plt.show()


## 랜덤으로 다수 클래스(1번 클래스) 샘플을 줄여 클래스 균형을 맞춤.

(3) 토믹 샘플링 (Tomek Links)

from imblearn.under_sampling import TomekLinks

# 토믹 샘플링 수행
tl = TomekLinks()
x_tl, y_tl = tl.fit_resample(x, y)

# 샘플링 결과 확인
print(Counter(y_tl))

# 시각화
plt.scatter(x_tl[:, 0], x_tl[:, 1], c=y_tl)
plt.show()


## 토믹 샘플링은 서로 다른 클래스가 가까이 붙어 있는 샘플을 제거하는 방법으로, 경계를 더 명확하게 만듦.

(4) 차원 축소 (PCA) 및 시각화

from sklearn.decomposition import PCA

# PCA 모델 선언 (2차원으로 축소)
pca = PCA(n_components=2)

# 원본 데이터 차원 축소
x_pca = pca.fit_transform(x)

# 시각화
plt.figure(figsize=(24, 6))

plt.subplot(1, 4, 1)
plt.scatter(x_pca[y==0, 0], x_pca[y==0, 1], label='class 0')
plt.scatter(x_pca[y==1, 0], x_pca[y==1, 1], label='class 1')
plt.title('Original')
plt.legend()


## 20차원 데이터를 2차원으로 축소하여 시각화함.

---

이걸 하루에 다 하는 게 맞나?