어제 분류 모델에 이어 회귀 모델까지 성공적으로 구현했다. 차근차근해보니 내가 순서를 잘못 공부했다는 것을 알게 됐다. 내일은 다시 미션 문제를 풀어봐야겠다.

학습시간 22:00~02:00(당일4H/누적214H)

◆ 오늘 깨달은 것

• 라쏘, 릿지, 엘라스틱넷은 선형회귀를 기본적으로 포함하고 있기 때문에 LinearRegression 함수를 호출하지 않아도 된다. 그래서 라쏘 회귀, 릿지 회귀, 엘라스틱넷 회귀라고 부른다.

• 다항식 변환은 스케일링 전에 한다.

• 다중공선성 확인 및 변환은 다항식 변환 후, 스케일링 전에 한다.

◆ 선형회귀 공부

보스턴 집값 예측

1. 데이터 전처리

df = pd.read_csv('data/boston.csv')
df.head()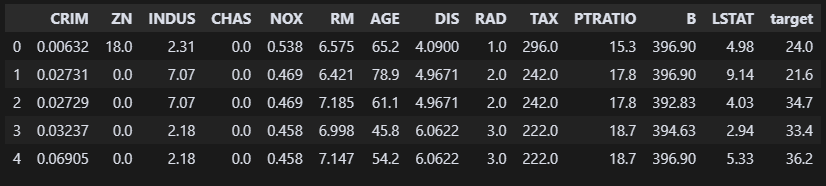

빠르게 데이터 전처리를 진행해 보자! 파일을 확인하니 컬럼이 14개다. 집값은 target이겠지?

df.info()
df.isna().sum()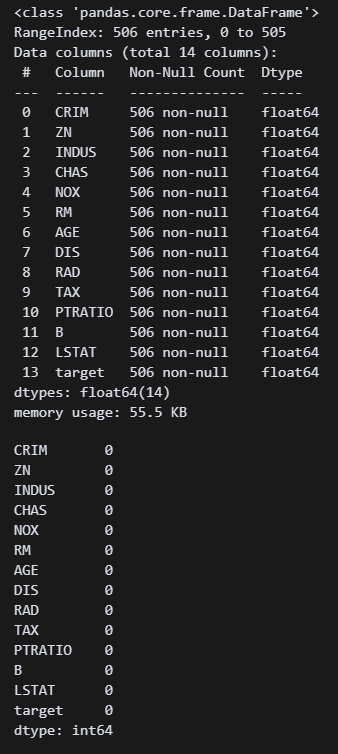

오 뭐야 이거 결측값도 없고 중복값도 없다...?

df.describe().loc[['min', 'mean', '50%', 'max']].T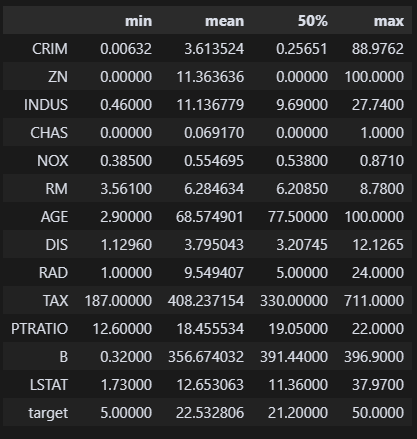

이상치를 확인했다. CRIM 평균이 3.6인데 88.9가 맥스면 조금 이상한 것 같다. ZN도 뭔지는 잘 모르겠지만 mean max 괴리가 있다. 각 컬럼마다 무슨 뜻인지 모르니까 접근하기가 어렵네. 이래서 컬럼명을 잘 지어야 하는 거구나.

df['CRIM'].value_counts()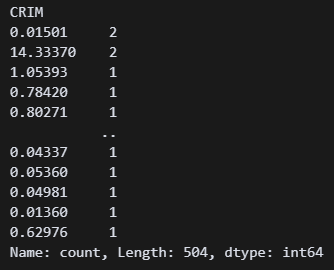

????????? 뭘까 이 수치는.. 어쩌면 CRIM 88.9가 정상일지도 모르겠다는 생각이 들었다.

df['ZN'].value_counts()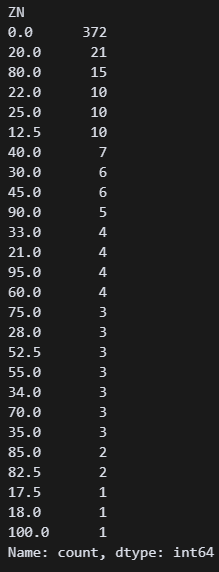

ZN의 의미는 모르겠지만 80이 15개나 있는 것을 봐선 100도 있을 수 있겠다는 생각이 들었다.

sns.heatmap(df.corr(), annot=True, fmt='0.1f')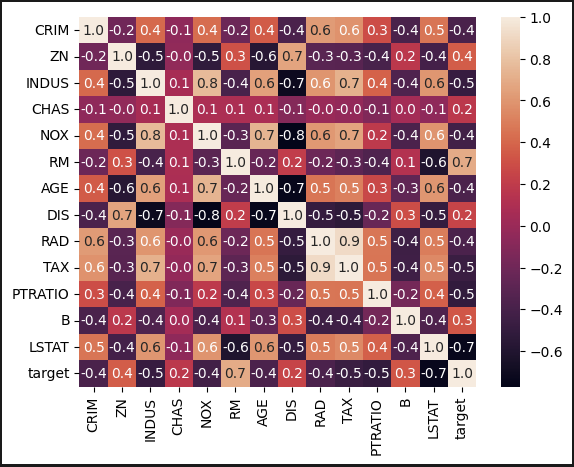

오늘도 상관관계 분석을 메인으로 하는 게 아니기 때문에 디자인은 건들지 않았다. 근데 target과 대부분 관계가 있는 것으로 보인다. CHAS, DIS의 수치가 0.2로 가장 낮다. 도대체 무슨 뜻인까

전처리는 여기까지 하면 될 것 같다.

2. 데이터 스플릿

스플릿 하기 전에 다중공선성을 먼저 확인해야겠다.

from statsmodels.stats.outliers_influence import variance_inflation_factor

VIF = df.astype(float) # 데이터를 float 타입으로 변환
pd.DataFrame(X.columns, columns=["Feature"])["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
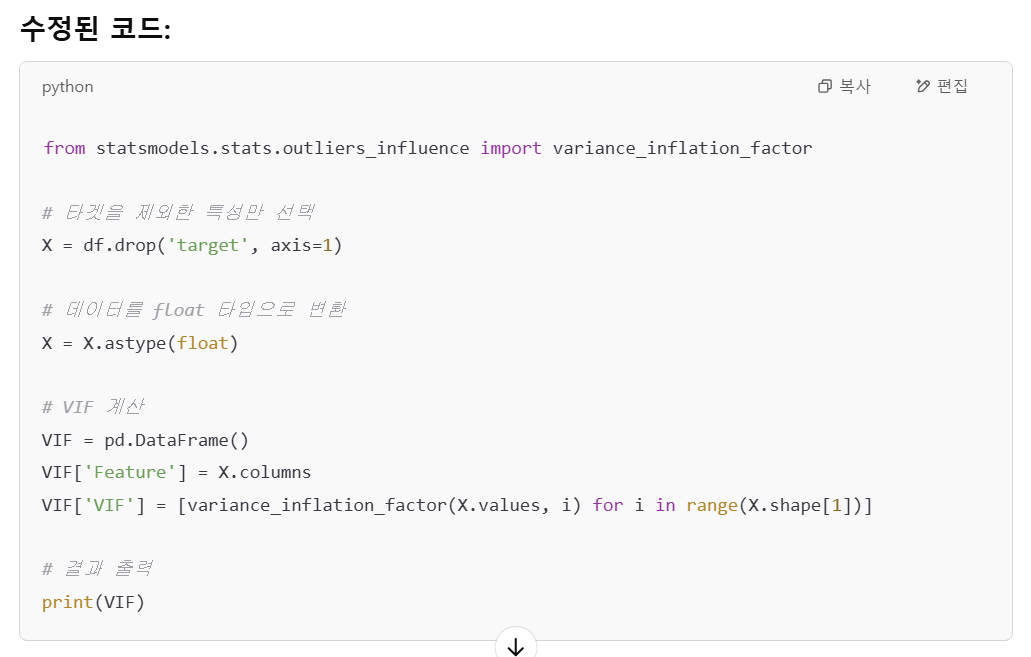
print(VIF) # Variance Inflation Factor

???? 수치가 너무 높은데? 이거 문제가 있는 거 아닌가? 10 이하로 맞춰야 한다고 들었던 것 같은데...

도와줘요 지선생
아하, 데이터를 먼저 독립변수와 종속변수로 나누고 진행해야 한다고 하네.

X = df.drop(columns='target')
y = df['target']

from statsmodels.stats.outliers_influence import variance_inflation_factor

V = df.astype(float)
VIF = pd.DataFrame()
VIF['Feature'] = V.columns
VIF['VIF'] = [variance_inflation_factor(V.values, i) for i in range(V.shape[1])]

print(VIF)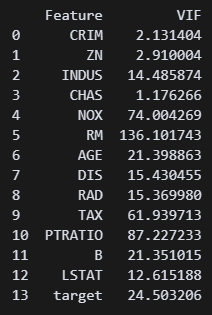

?? 그래도 수치가 너무 높은데 우짜냐 이거

도와줘요 지선생

차원축소나 라쏘 규제를 넣으며 된다고 한다. 차원축소는 아직 이해하지 못했으니 라쏘 정규화를 하고 선형회귀를 해야겠다.
?? 근데 코드가 조금 이상하다. 선형회귀 코드는 없고 라쏘 정규화 코드만 있다?? 라쏘만 해도 선형회귀가 되는 건가? 그리고 다항식 변환을 왜 스케일링보다 먼저 하는 거지?
헐. 라쏘 규제는 기능이 추가된 선형회귀인 거구나! 그래서 라쏘 회귀라고 하는 거구만!!!
오호라! 이제 확실해졌다.
깨달음2
깨달음3
깨달음4
깨달음5

결국 회귀의 순서는 아래와 같다.

• 데이터 스플릿 - 다항식 변환 - 다중공선성 확인 - 스케일링 - 학습

# 1. 데이터 분할
X = df.drop(columns='target')  
y = df['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 2. 다항식 변환 (2차항 생성)
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)

# 3. 다중공선성 확인 (스케일링 전)
vif_data = pd.DataFrame()
vif_data["Feature"] = poly.get_feature_names_out(X.columns)
vif_data["VIF"] = [variance_inflation_factor(X_train_poly, i) for i in range(X_train_poly.shape[1])]
print(vif_data)  # VIF 값 확인

# 4. 다중공선성이 높은 특성 제거 (예: VIF > 10인 경우)
high_vif_features = vif_data[vif_data["VIF"] > 10]["Feature"].values
print(f"VIF 높은 특성 제거: {high_vif_features}")

# 5. 다중공선성이 높은 특성을 제외한 새로운 데이터셋 생성
X_train_poly_df = pd.DataFrame(X_train_poly, columns=poly.get_feature_names_out(X.columns))
X_test_poly_df = pd.DataFrame(X_test_poly, columns=poly.get_feature_names_out(X.columns))

X_train_poly_df = X_train_poly_df.drop(columns=high_vif_features, errors='ignore')
X_test_poly_df = X_test_poly_df.drop(columns=high_vif_features, errors='ignore')

# 6. 스케일링
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train_poly_df)
X_test_scaled = scaler.transform(X_test_poly_df)

이 코드는 저장해 뒀다가 나중에 해봐야겠다. 일단 모델 구현이 먼저니 다중이는 나중에 만나는 것으로.

다시 본론으로 돌아와서,

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=30)

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)

데이터 스플릿 후 다항식으로 변환했다. 일단 2차로 해봐야겠다.

3. 모델 학습

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scl = scaler.fit_transform(X_train)
X_test_scl = scaler.transform(X_test)

from sklearn.linear_model import Lasso
lasso = Lasso(alpha=0.01)
lasso.fit(X_train_scl, y_train)

스케일링 후 라쏘회귀 모델에 학습시켰다. scaler.transform 테스트셋에 _fit 없는 것도 잘 확인했다.

y_train_pred = lasso.predict(X_train_scl)
y_test_pred = lasso.predict(X_test_scl)

제발 잘 예측해주렴!

4. 모델 평가

from sklearn.metrics import accuracy_score, confusion_matrix, classification_report

print("Accuracy_train:", accuracy_score(y_train, y_train_pred))
print("Accuracy_test:", accuracy_score(y_test, y_test_pred))
print("Confusion Matrix:\n", confusion_matrix(y_test, y_test_pred))
print("Classification Report:\n", classification_report(y_test, y_test_pred))

뭐지? 평가지표를 넣었는데 에러가 떴다.

아, 가만 보니까 분류모델 평가용 코드를 넣었다 ㅋ

from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score

print("Train set metrics")
print("Train MAE:", mean_absolute_error(y_train, y_train_pred))
print("Train MSE:", mean_squared_error(y_train, y_train_pred))
print("Train RMSE:", mean_squared_error(y_train, y_train_pred) ** 0.5)
print("Train R2 Score:", r2_score(y_train, y_train_pred))
print("--------------------------------")
print("Test set metrics")
print("Test MAE:", mean_absolute_error(y_test, y_test_pred))
print("Test MSE:", mean_squared_error(y_test, y_test_pred))
print("Test RMSE:", mean_squared_error(y_test, y_test_pred) ** 0.5)
print("Test R2 Score:", r2_score(y_test, y_test_pred))

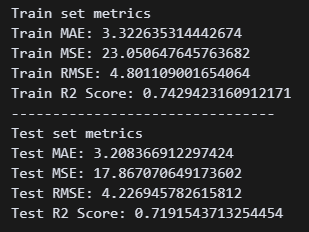오..! 모델이 잘 학습한 것 같다. 이유는 모르겠지만 테스트 셋의 점수가 훨씬 좋다.

from sklearn.model_selection import learning_curve

train_sizes, train_scores, test_scores = learning_curve(lasso, X, y, cv=5)

# 평균 정확도 계산
train_mean = train_scores.mean(axis=1)
test_mean = test_scores.mean(axis=1)

# 그래프 그리기
plt.figure(figsize=(10, 7))
plt.plot(train_sizes, train_mean, color='blue', label='Train Accuracy')
plt.plot(train_sizes, test_mean, color='red', label='Test Accuracy')
plt.title('Learning Curve')
plt.xlabel('Training Size')
plt.ylabel('Accuracy')
plt.legend()
plt.show()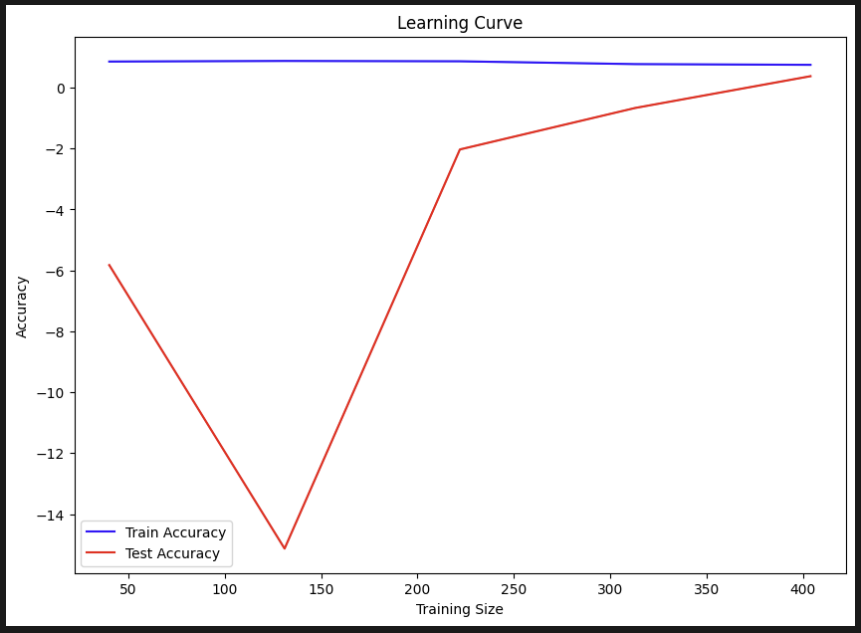

어제 배운 러닝커브를 그대로 사용해봤다. 근데 정확도가 0은 뭔가 조금 이상하다??
아하! 분류는 정확도를 써도 되지만 회귀는 평균오차로 해야한다.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import learning_curve

# 러닝 커브 계산 (MSE 사용)
train_sizes, train_scores, test_scores = learning_curve(
    lasso, X, y, cv=5, scoring="neg_mean_squared_error")

# 평균 및 표준편차 계산
train_mean = -train_scores.mean(axis=1)  # 음수값을 양수로 변환
test_mean = -test_scores.mean(axis=1)    # 음수값을 양수로 변환

# 그래프 그리기
plt.figure(figsize=(10, 7))
plt.plot(train_sizes, train_mean, color='blue', label='Train MSE')
plt.plot(train_sizes, test_mean, color='red', label='Test MSE')

plt.title('Learning Curve (MSE)')
plt.xlabel('Training Size')
plt.ylabel('Mean Squared Error')
plt.legend()
plt.grid()
plt.show()

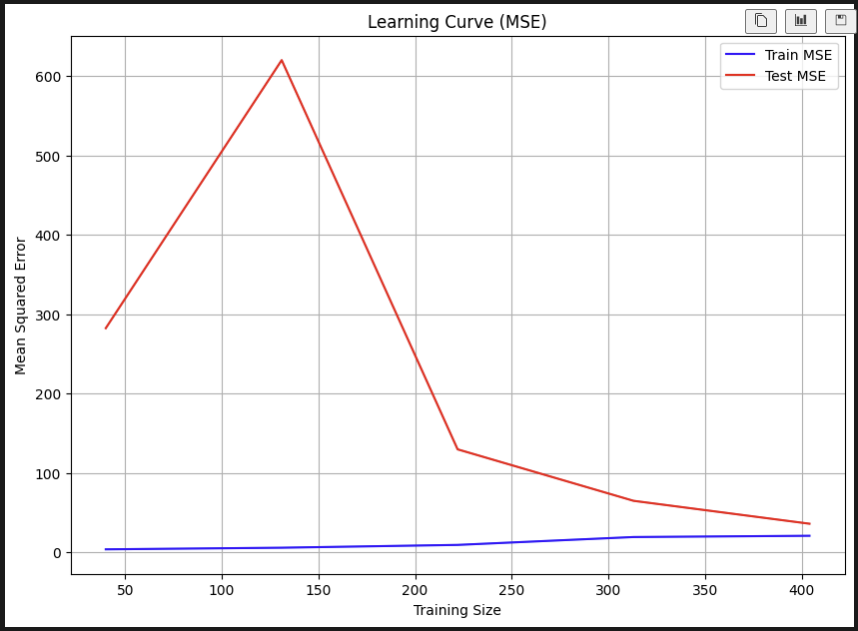오 갈수록 테스트셋의 오차가 줄어드는 게 보인다!

---

고마워요 지선생! 회귀 모델 성공적!