머신러닝은 몸풀기였다.
학습시간 09:00~02:00(당일17H/누적311H)
◆ 학습내용
1. 딥러닝이란?
(1) 딥러닝의 정의
- 뇌의 신경세포(뉴런)를 모방하여 정보를 전달하고 처리
- 인공신경망(Artificial Neural Network)을 여러 층으로 쌓아올린 모델
- 고차원 데이터에서 패턴을 비선형 방식으로 학습하는 체계
- 이미지, 음성, 텍스트 등 고차원 데이터를 비선형 방식으로 학습
- 핵심은 오차 역전파, 적절한 초기화, 하이퍼파라미터 조정, 적절한 손실함수
(2) 퍼셉트론과 딥러닝의 차이점
| 항목 | 퍼셉트론 (고전 모델) | 딥러닝 (현대 모델) |
|---|---|---|
| 출력 방식 | 이진 출력 (0 또는 1) | 확률 출력 (0~1) |
| 활성화 함수 | 계단 함수 | Sigmoid, ReLU 등 |
| 손실 함수 | 틀린 샘플만 학습 | 전체 오차 기반 학습 (Cross Entropy 등) |
| 미분 가능성 | ❌ | ✅ |
| 학습 방법 | 규칙 기반 | 경사하강법 기반 |
| 사용 시기 | 고전 AI | 현대 딥러닝의 핵심 |
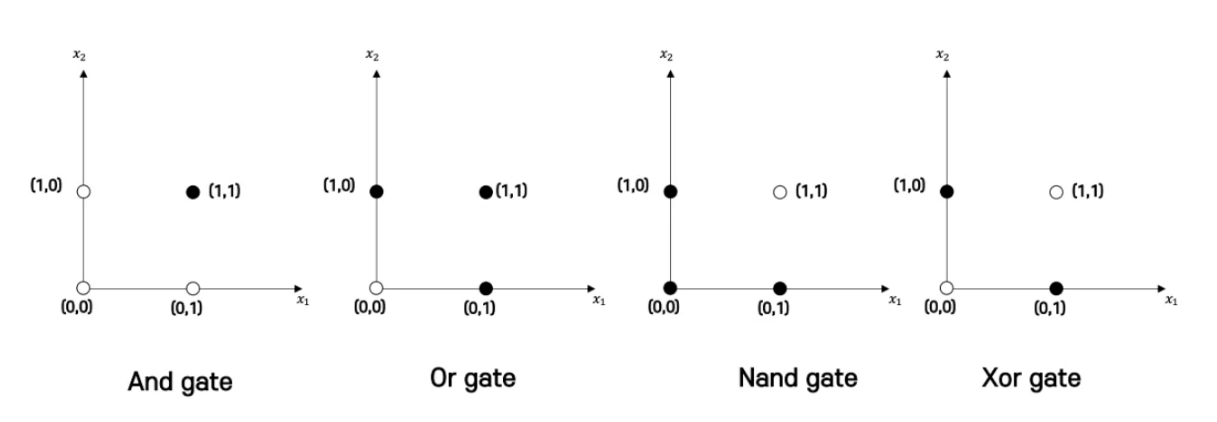퍼셉트론의 한계. Xor 게이트를 구분할 수 없음.
# 퍼셉트론 vs 딥러닝 시각화 (간단한 퍼셉트론 구현)
def perceptron(x, w, b):
output = sum(x_i * w_i for x_i, w_i in zip(x, w)) + b
return 1 if output > 0 else 0
x = [1, 0]
w = [0.5, -0.6]
b = 0.1
print(perceptron(x, w, b)) # 출력: 1 또는 0(3) 딥러닝이 어려운 이유
- 비선형성: 단순한 수학 모델로 예측 불가한 복잡한 구조
- 고차원성: 수많은 파라미터로 인해 탐색 공간이 커짐
- 그래디언트 소실/폭주 문제: 깊은 층에서 오차가 전달되지 않거나 폭발함
- 하이퍼파라미터 민감성: 적절한 설정 없이는 학습 실패 가능성 높음
2. 핵심 용어 정리
| 용어 | 정의 |
|---|---|
| 퍼셉트론 | 입력의 가중합을 계산하고 출력하는 단일 뉴런 모델 |
| 뉴런 (Neuron) | 하나의 계산 단위. 입력 받아 출력 생성 |
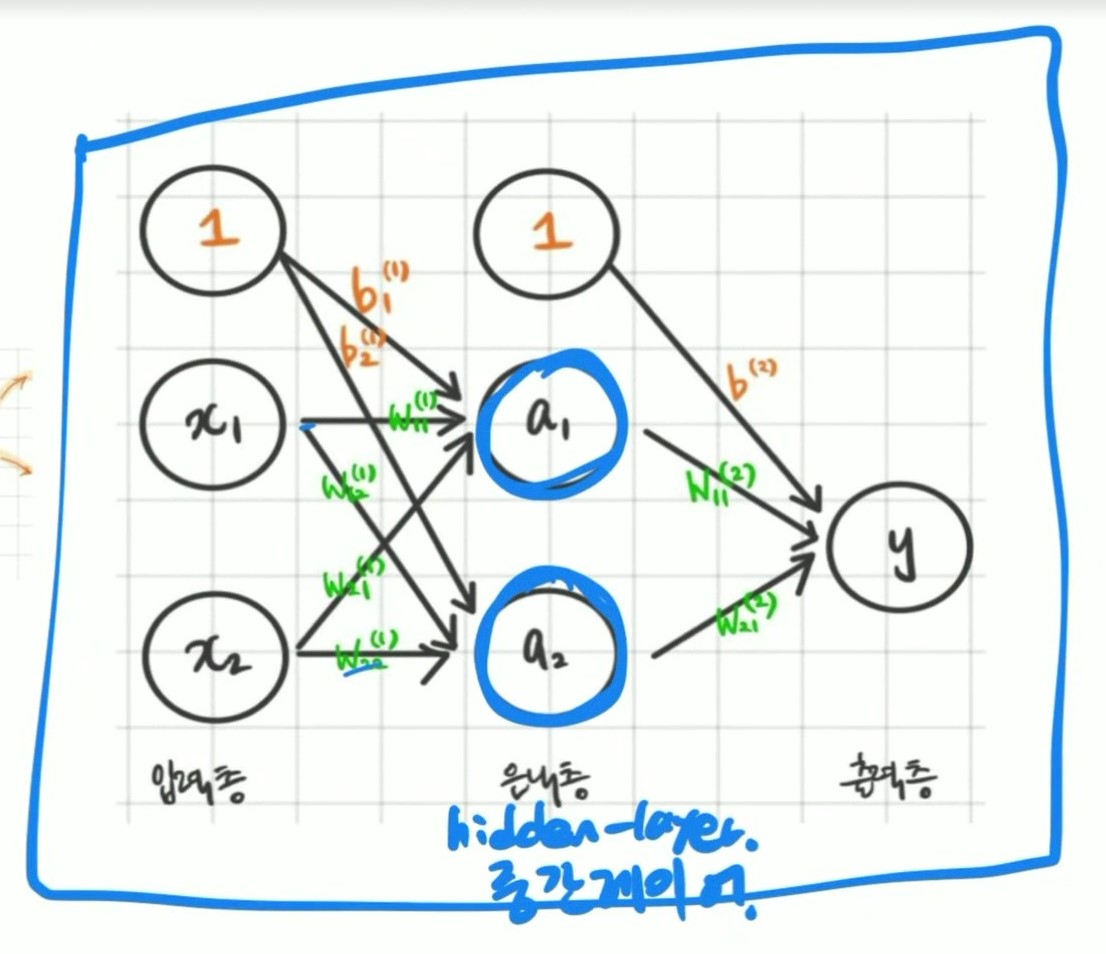
| 레이어 (Layer) | 뉴런들의 집합. 입력층, 은닉층, 출력층으로 구성 |
| 입력층 | 데이터가 처음 들어오는 층 |
| 은닉층 | 내부 연산이 일어나는 중간층 (1개 이상 가능) |
| 출력층 | 예측 결과가 나오는 마지막 층 |
| 순전파 (Forward Propagation) | 입력 → 출력 방향의 연산 흐름 |
| 역전파 (Backpropagation) | 오차를 역으로 전달하여 가중치 수정 |
| 가중치 (Weight) | 입력에 곱해지는 값으로 학습의 핵심 |
| 편향 (Bias) | 뉴런의 출력에 더해지는 상수 |
| 활성화 함수 | 비선형성을 부여해 복잡한 표현 학습 가능 |
| 초기화 (Initialization) | 가중치의 시작값 설정 방식 |
| 출력 함수 | 출력층에서 사용되는 활성화 함수 (e.g., softmax) |
| 손실 함수 (Loss Function) | 예측과 정답의 차이를 수치화한 함수 |
3. 딥러닝 모델 설계 시 고려 사항
(1) 하이퍼파라미터
- 학습률 (Learning Rate)
- 배치 크기 (Batch Size)
- 에폭 수 (Epochs)
- 드롭아웃 비율
(2) 손실 함수 종류
| 함수 | 사용 예시 | 수식 특징 |
|---|---|---|
| MSE | 회귀 | 평균 제곱 오차 |
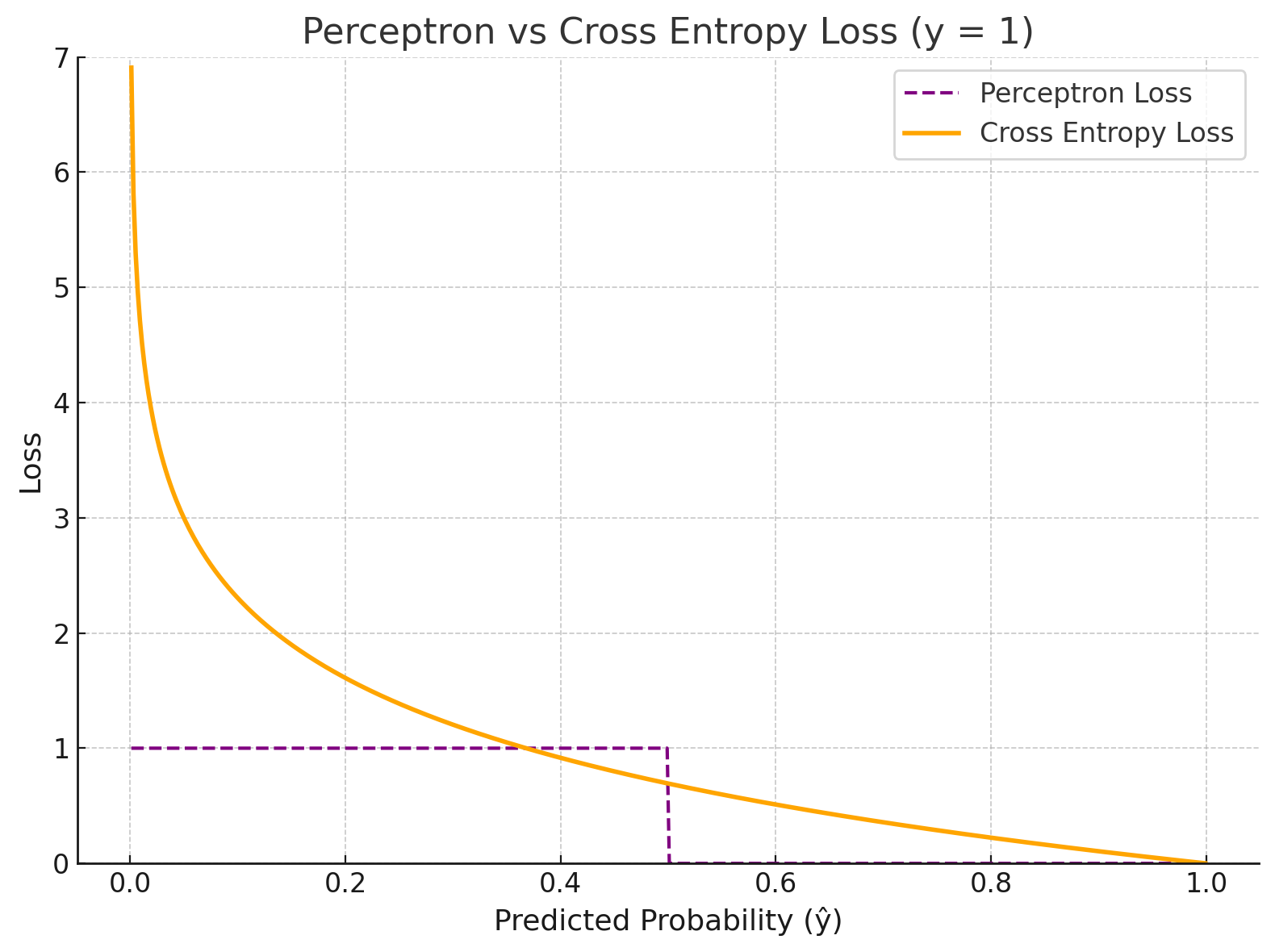
| Binary Cross Entropy | 이진 분류 | -[ylog(y^) + (1-y)log(1-y^)] |
| Categorical Cross Entropy | 다중 분류 | -∑yilog(y^i) |
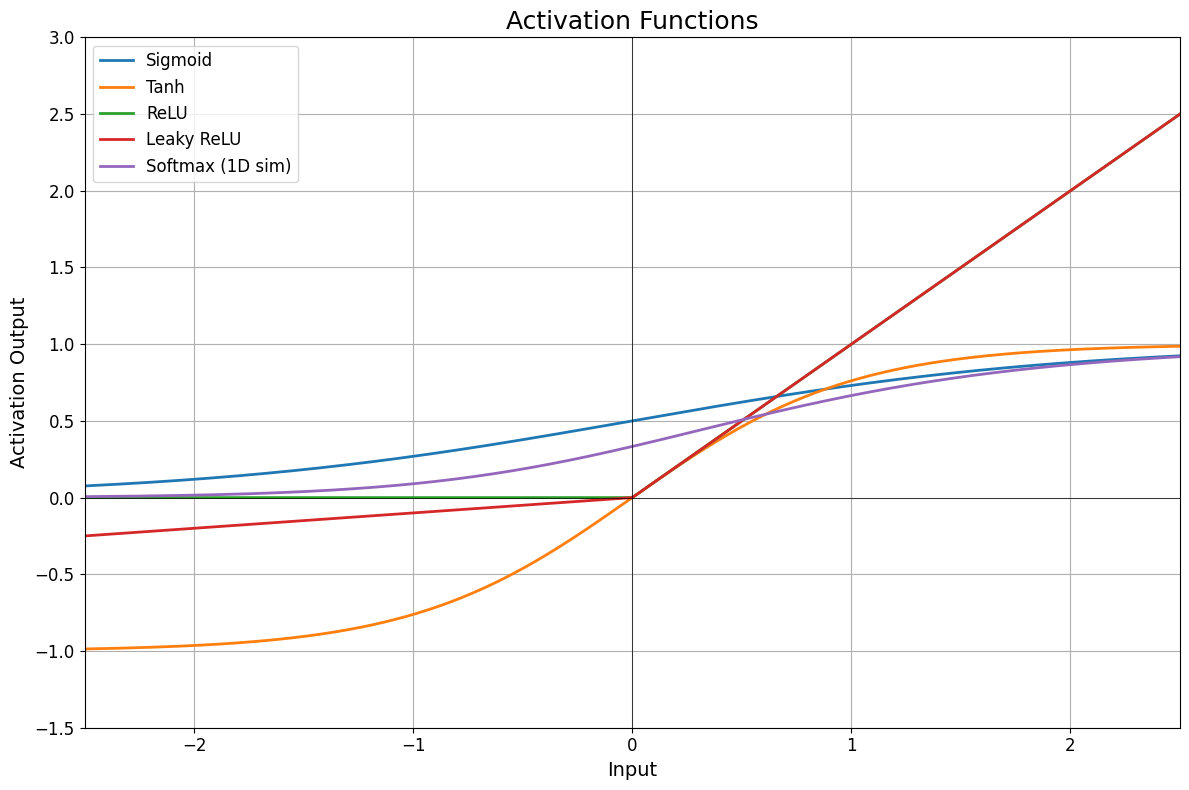
(3) 활성화 함수 종류
| 함수 | 범위 | 특징 | 사용 위치 |
|---|---|---|---|
| Sigmoid | (0, 1) | 확률 해석, gradient vanishing 위험 | 출력층 (이진) |
| Tanh | (-1, 1) | 0 중심, sigmoid보다 낫다 | 은닉층 |
| ReLU | [0, ∞) | 계산 단순, 빠름 | 은닉층 (기본) |
| LeakyReLU | (-∞, ∞) | 죽은 뉴런 문제 완화 | 은닉층 |
| Softmax | (0~1), 합=1 | 전체 클래스 확률화 | 출력층 (다중 분류) |
4. 최적화 알고리즘
(1) 경사하강법 종류
| 이름 | 특징 | 장단점 |
|---|---|---|
| GD | 전체 데이터로 기울기 계산 | 안정적, 느림 |
| SGD | 1개 샘플씩 업데이트 | 빠르지만 불안정 |
| Mini-Batch | N개씩 묶어서 업데이트 | 균형형 |
(2) 대표 옵티마이저
| 이름 | 설명 | 특징 |
|---|---|---|
| Momentum | 과거 기울기 고려 | 진동 완화 |
| RMSProp | 각 파라미터 학습률 다르게 | 수렴 빠름 |
| Adam | Momentum + RMSProp | 안정성 + 속도 최적 |
(3) 정규화/규제화
- Dropout: 일부 뉴런 임의로 꺼 학습 일반화
- L1/L2: 가중치 크기 제한해 과적합 방지
- Early Stopping: 검증 손실 멈추면 조기 종료
5. 오차 역전파 (Backpropagation)
(1) 개념과 원리
- 오차 역전파는 딥러닝 학습의 핵심 알고리즘
- 손실 함수로부터 시작해, 각 층의 파라미터(가중치, 편향)에 대해 손실의 기울기(Gradient)를 계산
- 이 기울기를 이용해 경사하강법으로 파라미터를 업데이트함
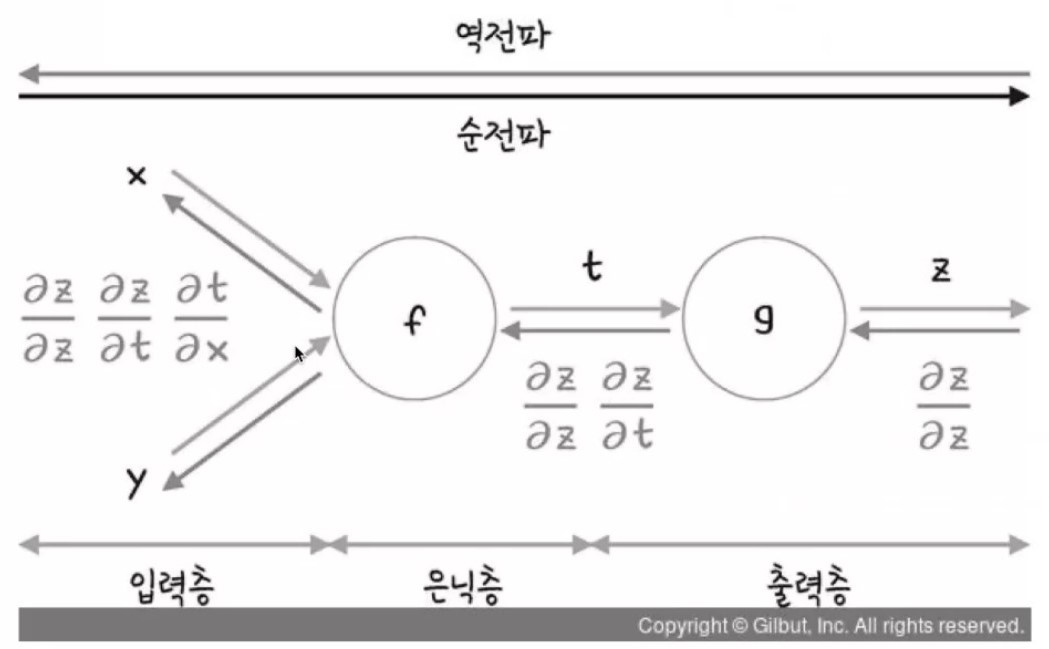
- 체인 룰(연쇄 법칙, Chain Rule)을 기반으로 연속적인 함수의 미분을 층마다 역으로 적용
# 간단한 체인룰 예시
import torch
x = torch.tensor(2.0, requires_grad=True)
y = x**2 + 3*x + 1
y.backward()
print(x.grad) # dy/dx = 2x + 3 = 7이처럼 딥러닝에서는 z → a → y^ → L 형태의 연쇄 함수 구조가 반복되며,
손실 L이 각 가중치 W에 어떻게 영향을 주는지 체인 룰로 추적하게 됨.
(2) 오차 역전파의 주요 단계 요약
| 단계 | 수식 기호 | 의미 |
|---|---|---|
| 1단계 | ∂L/∂ŷ | 출력값이 바뀔 때 손실이 얼마나 변하는가? (손실 함수의 기울기) |
| 2단계 | ∂ŷ/∂z | z값(활성화 전 가중합)이 바뀔 때 출력이 어떻게 변하는가? (활성화 함수의 미분) |
| 3단계 | ∂z/∂W | 가중치 W가 바뀔 때 z가 어떻게 변하는가? (입력 x에 대한 기울기) |
| 🔄 전체 | ∂L/∂W = ∂L/∂ŷ × ∂ŷ/∂z × ∂z/∂W | 체인 룰로 미분을 연결하여 가중치에 대한 손실의 변화율 계산 |
(3) 전체 오차 역전파 루프 예시
# PyTorch 예시 (2층 신경망 역전파)
import torch
import torch.nn as nn
# 입력, 정답
x = torch.tensor([[1.0, 2.0]], requires_grad=True)
y = torch.tensor([[0.0]])
# 간단한 모델 정의
model = nn.Sequential(
nn.Linear(2, 1),
nn.Sigmoid()
)
# 손실 함수 및 옵티마이저
criterion = nn.BCELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
# 순전파 → 손실 계산 → 역전파
output = model(x)
loss = criterion(output, y)
loss.backward() # 여기서 체인 룰로 각 가중치에 대한 ∂L/∂W 계산됨
optimizer.step()(4) 요약
- 오차 역전파는 단순히 "오차를 뒤로 돌려 보내면서" 가중치를 조정하는 방식이 아님
- 정확히는, 각 가중치가 손실에 얼마나 기여했는지를 수학적으로 계산하는 과정
- 이 정보는 결국 모델이 "무엇이 잘못되었는지"를 학습하게 해주는 피드백
"오차 역전파는 딥러닝에게 생각을 가르치는 방식이다."
6. 초기화 방법
(1) 초기화의 필요성
- 딥러닝 학습에서 초기 가중치 설정은 매우 중요함
- 초기 가중치가 부적절하면 아래 문제가 발생:
- Gradient Vanishing: 기울기가 0에 가까워져서 학습이 멈춤
- Gradient Exploding: 기울기가 너무 커져서 발산하며 학습 실패
- 모든 뉴런이 동일한 값으로 초기화되면 대칭성(symmetricity)이 깨지지 않아, 뉴런들이 같은 값만 학습하게 됨 → ❌
(2) 초기화 방식 비교
| 이름 | 수식 기준 | 특징 | 추천 상황 |
|---|---|---|---|
| 0 초기화 | 0 | ❌ 모든 뉴런이 동일하게 학습 | 절대 비추천 |
| 정규분포 랜덤 | N(0,1) | 평균 0, 표준편차 1 | 기본, 하지만 불안정 가능 |
| 균등분포 랜덤 | U(-a, a) | -0.5~0.5 범위 등 | gradient 흐름 불안정 가능 |
| Xavier (Glorot) | 1 / sqrt(n_in) | 입력/출력 수 기반 분산 조절 | sigmoid, tanh 계열에 적합 |
| He 초기화 | 2 / sqrt(n_in) | ReLU 계열에 적합, 큰 분산 | 깊은 네트워크에 안정적 |
| LeCun 초기화 | 1 / sqrt(n_in) | SELU 전용 | 특수 구조에서 사용 |
Xavier, He, LeCun 모두 뉴런의 개수에 따라 분산을 조정하여 gradient 흐름을 조절함.
(3) 코드 예시
import torch.nn as nn
import torch.nn.init as init
layer = nn.Linear(256, 128)
# Xavier 초기화
init.xavier_uniform_(layer.weight)
# He 초기화
init.kaiming_normal_(layer.weight, nonlinearity='relu')(4) 요약
좋은 초기화는 역전파에서 gradient가 사라지지 않도록 한다.
- ReLU → He
- Sigmoid or Tanh → Xavier
- SELU → LeCun
7. 딥러닝 모델 구현 순서
| 단계 | 이름 | 설명 |
|---|---|---|
| 1️⃣ | 데이터 준비 | 전처리, 정규화, 나누기 |
| 2️⃣ | 모델 구조 정의 | 층 수, 뉴런 수, 활성화 함수 설정 |
| 3️⃣ | 하이퍼파라미터 설정 | 학습률, 배치 크기, 에폭수 등 |
| 4️⃣ | 초기화 | Xavier, He 등 |
| 5️⃣ | 손실 함수 설정 | MSE, CrossEntropy 등 |
| 6️⃣ | 옵티마이저 설정 | Adam 등 선택 |
| 7️⃣ | 훈련 루프 | 순전파 → 손실 → 역전파 → 업데이트 |
| 8️⃣ | 평가 | validation, test |
| 9️⃣ | 튜닝 | 하파 조정, 성능 개선 반복 |
머리아파요 강사님 ㅠㅠ
나는 AI 엔지니어가 된다.