Calculus for Machine Learning and Data Science - Week 3

Optimization in Neural Networks

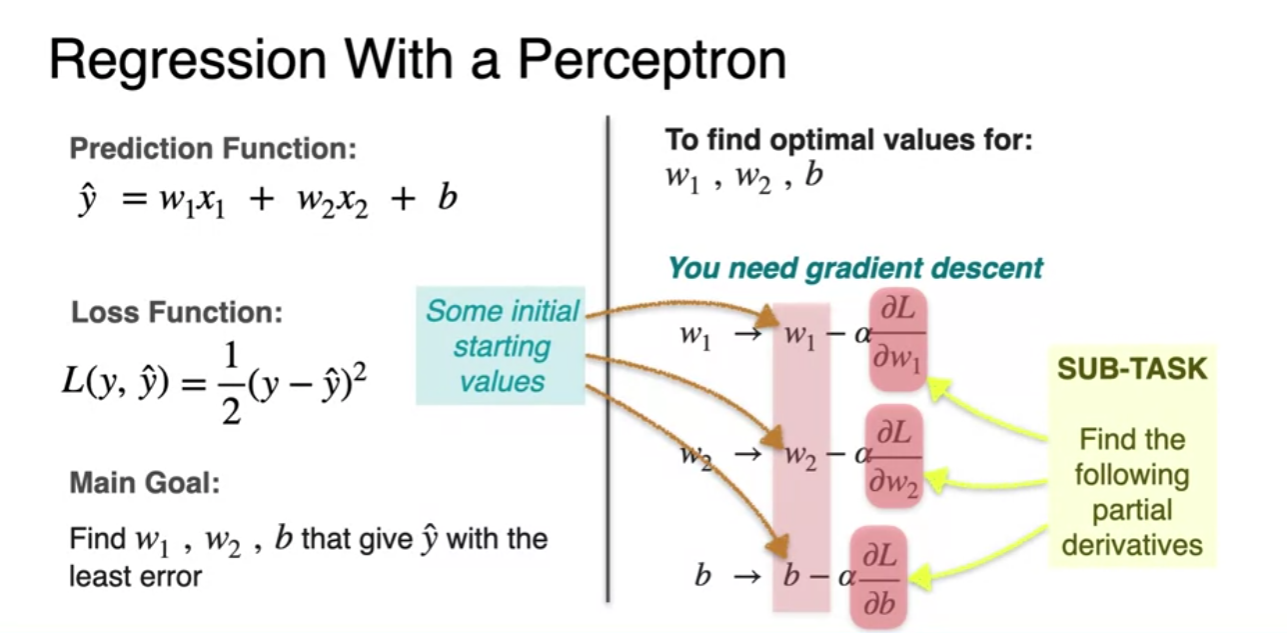
Regression with a perception

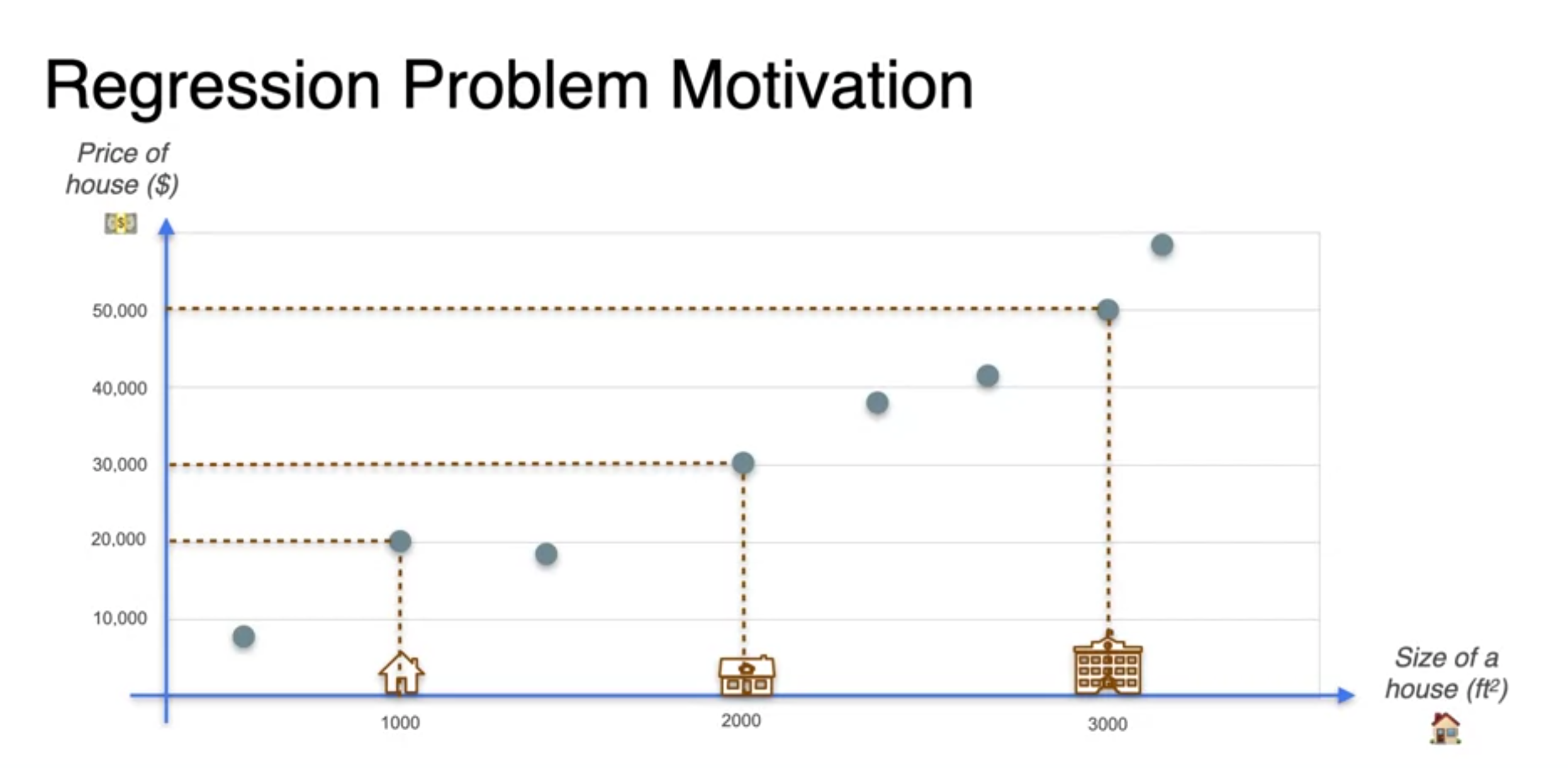
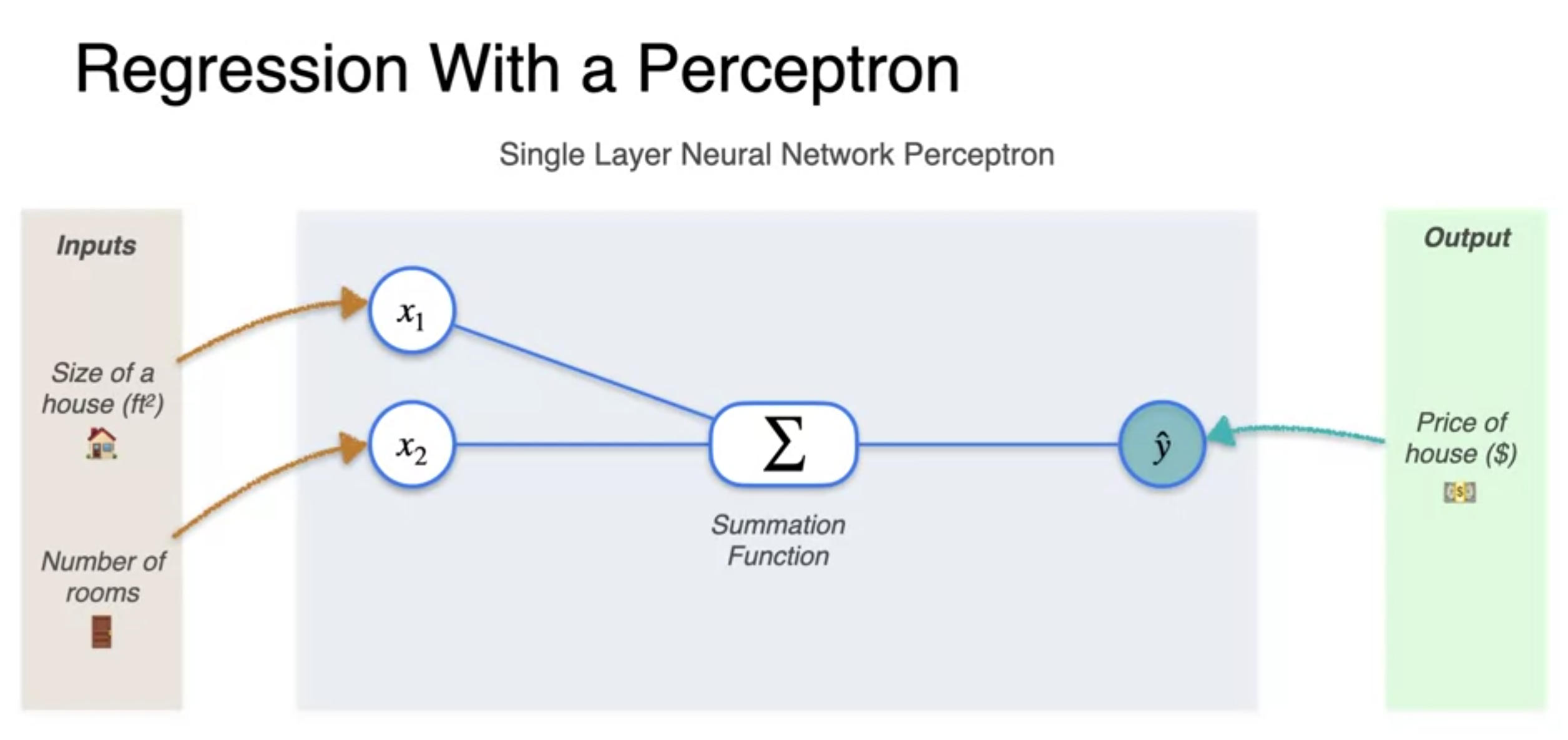
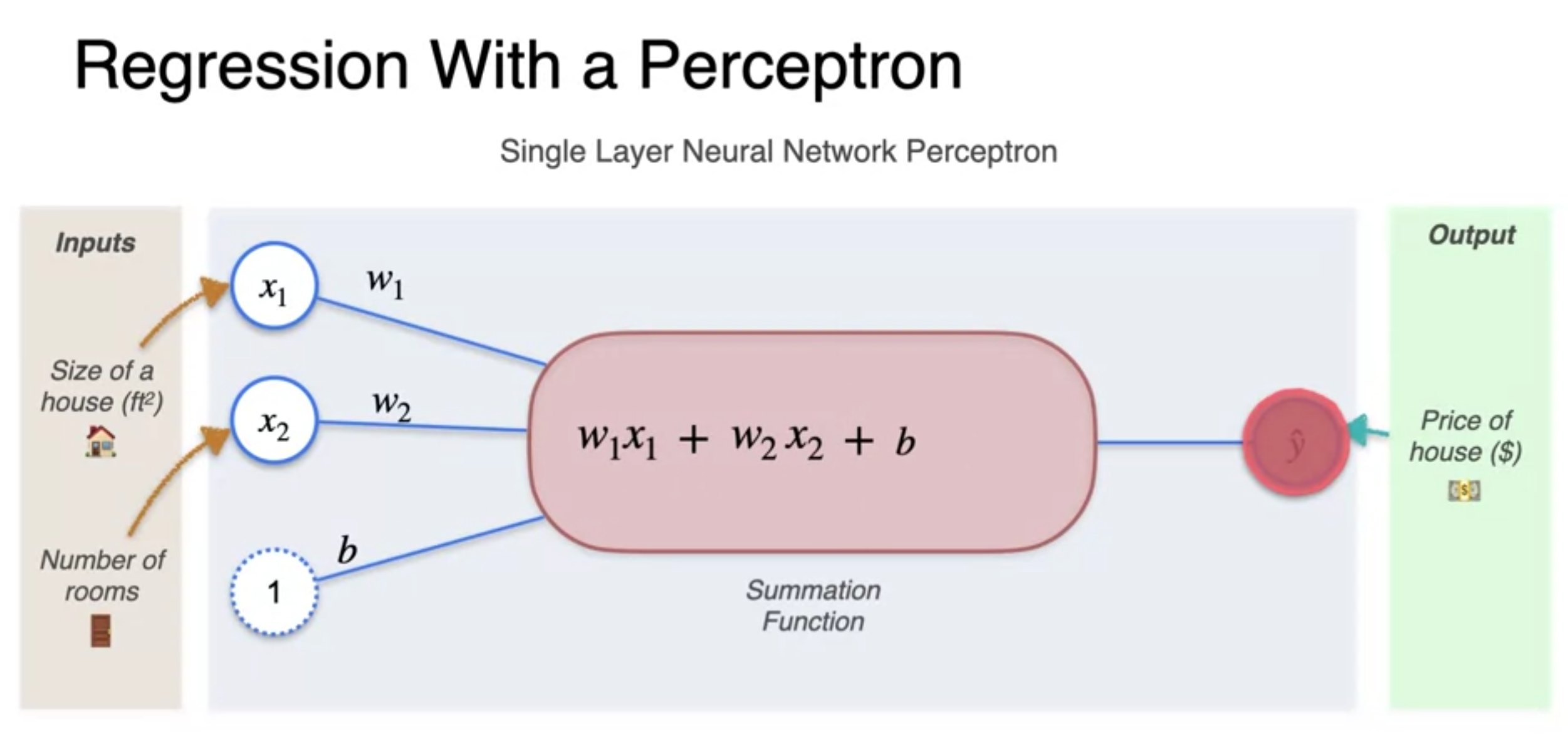
• 신경망(percetptron) : takes some inputs to output we want to predict

Regression with a perceptron - Loss function

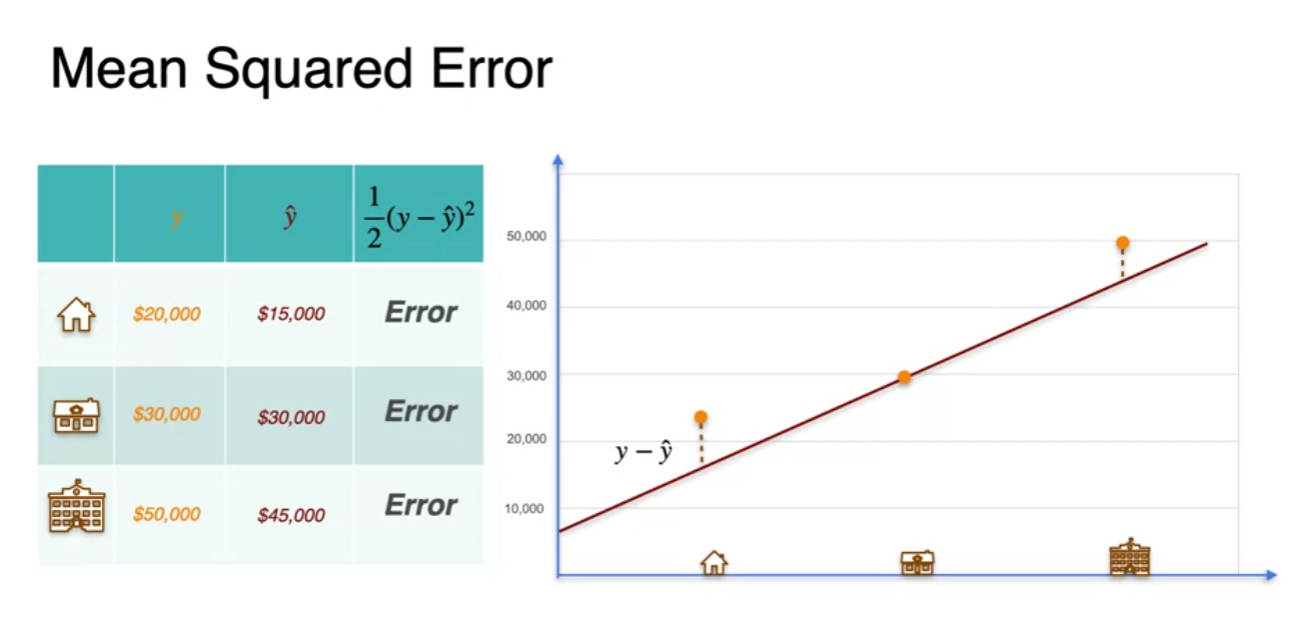
• For handle positive error and negative one same we square the error
• multiplying by half : cosmetic reason(y-y')^2 derivative get a lingering two

Regression with a perceptron - Gradient Descent

Classification with Perceptron

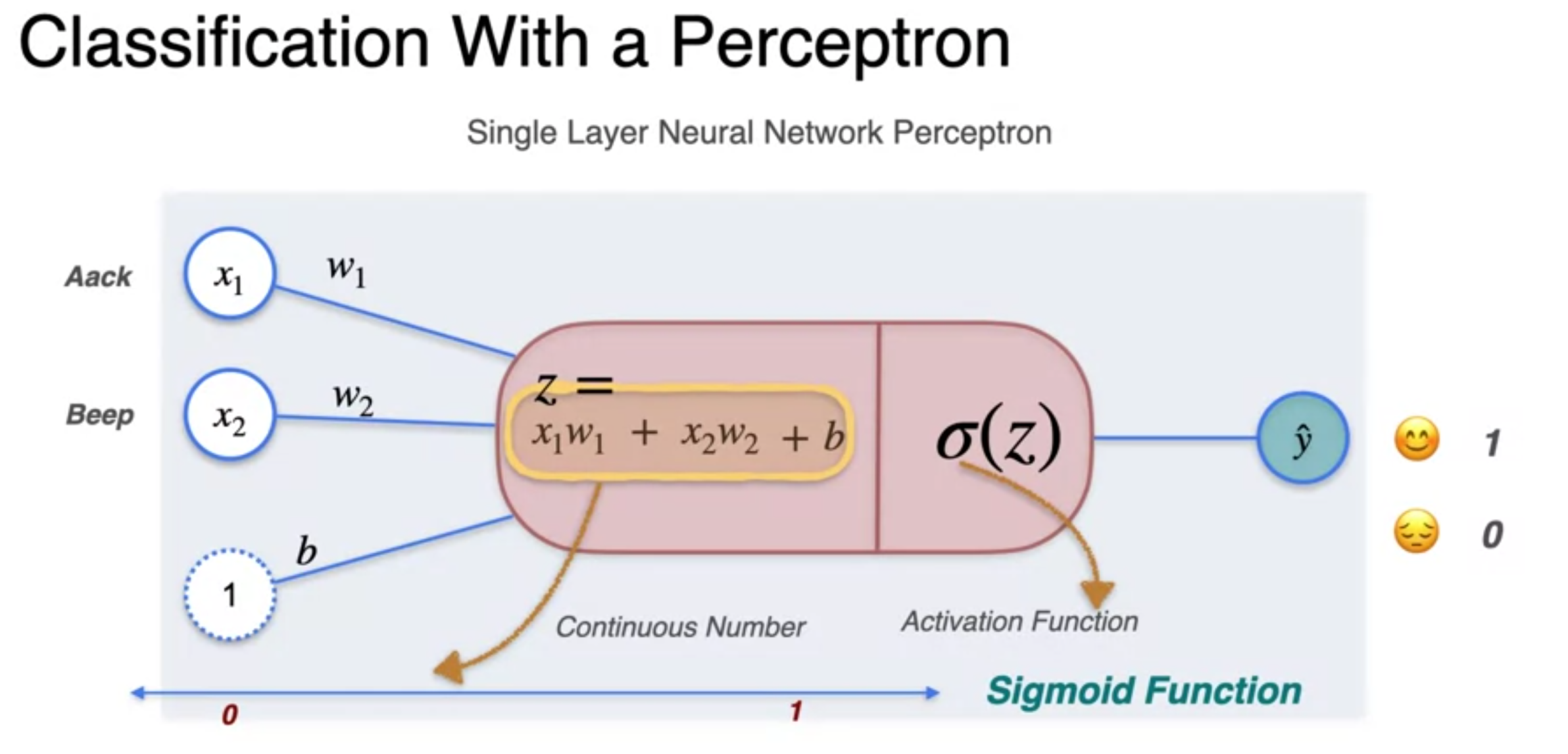
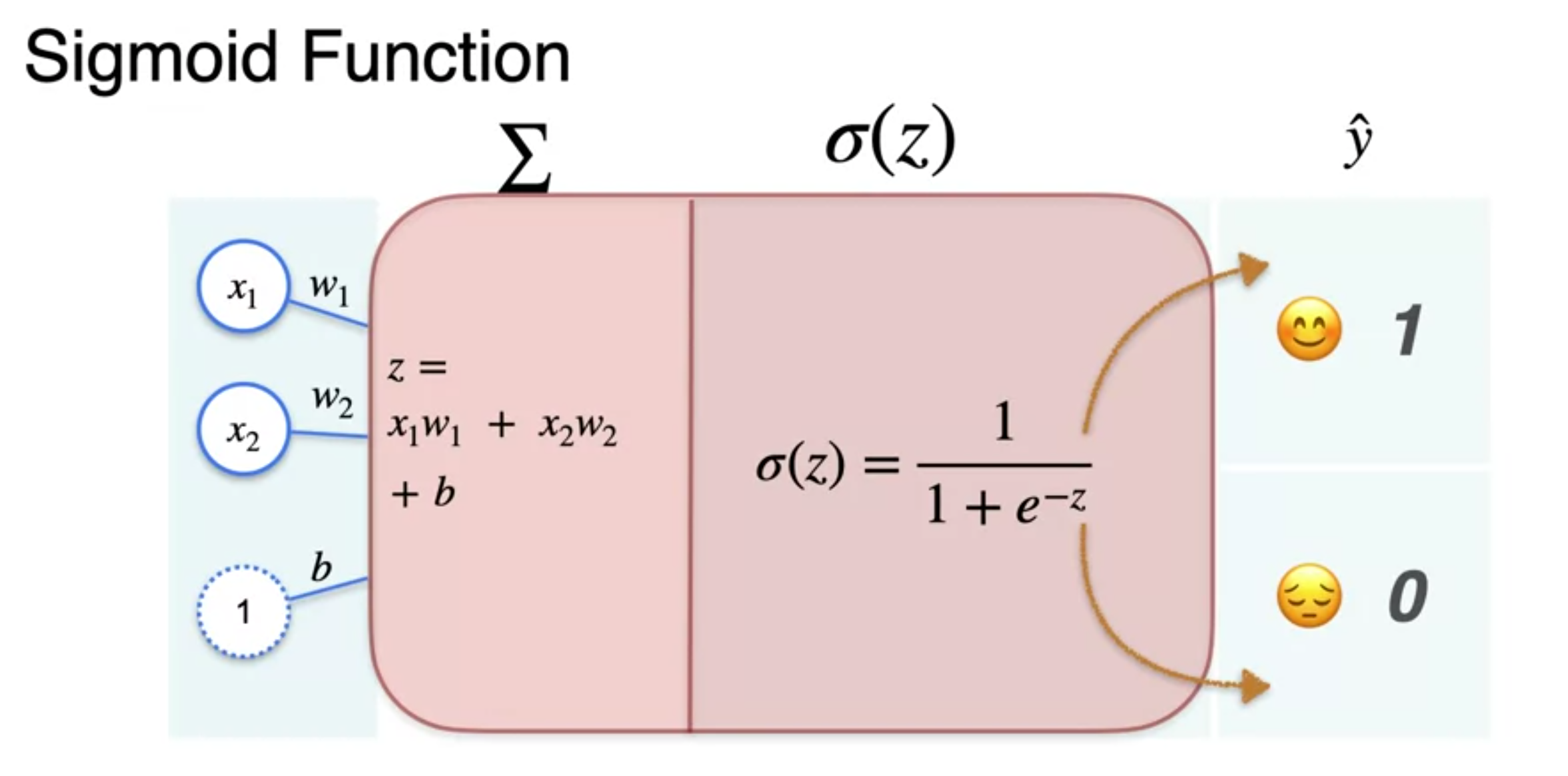
• Activation function : crunch the number interval 1 and 0
  • Sigmoid function : $S(x) = \frac{1}{1 + e^{-x}}$

Classification with Perceptron - The sigmoid function

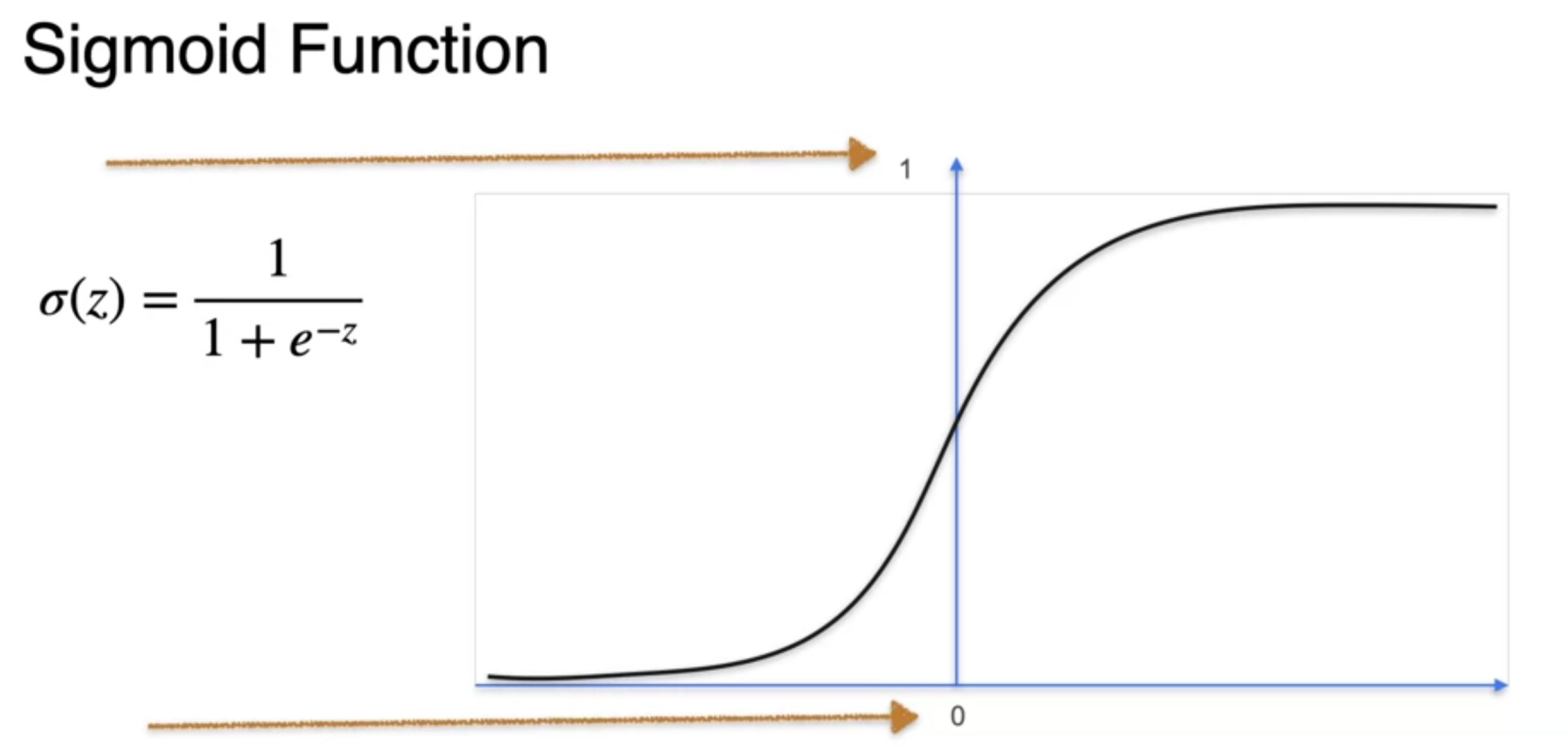
Q. why sigmoid is useful?
A. Its derivatives is really nice

• $\sigma(z) = (1+e^{-z})^{-1}$
  • chain rule $\frac{d}{dz}\sigma(z)$가
  • ${-1}(1+e^{-z})^{-1-1}(\frac{d}{dz}(1+e^{-z}))$

• at the end the derivatives of sigmoid is
  • $\frac{d}{dz}\sigma(z) = \sigma(z)(1-\sigma(z))$
  • It looks beautiful

Classification with Perceptron - Gradient Descent

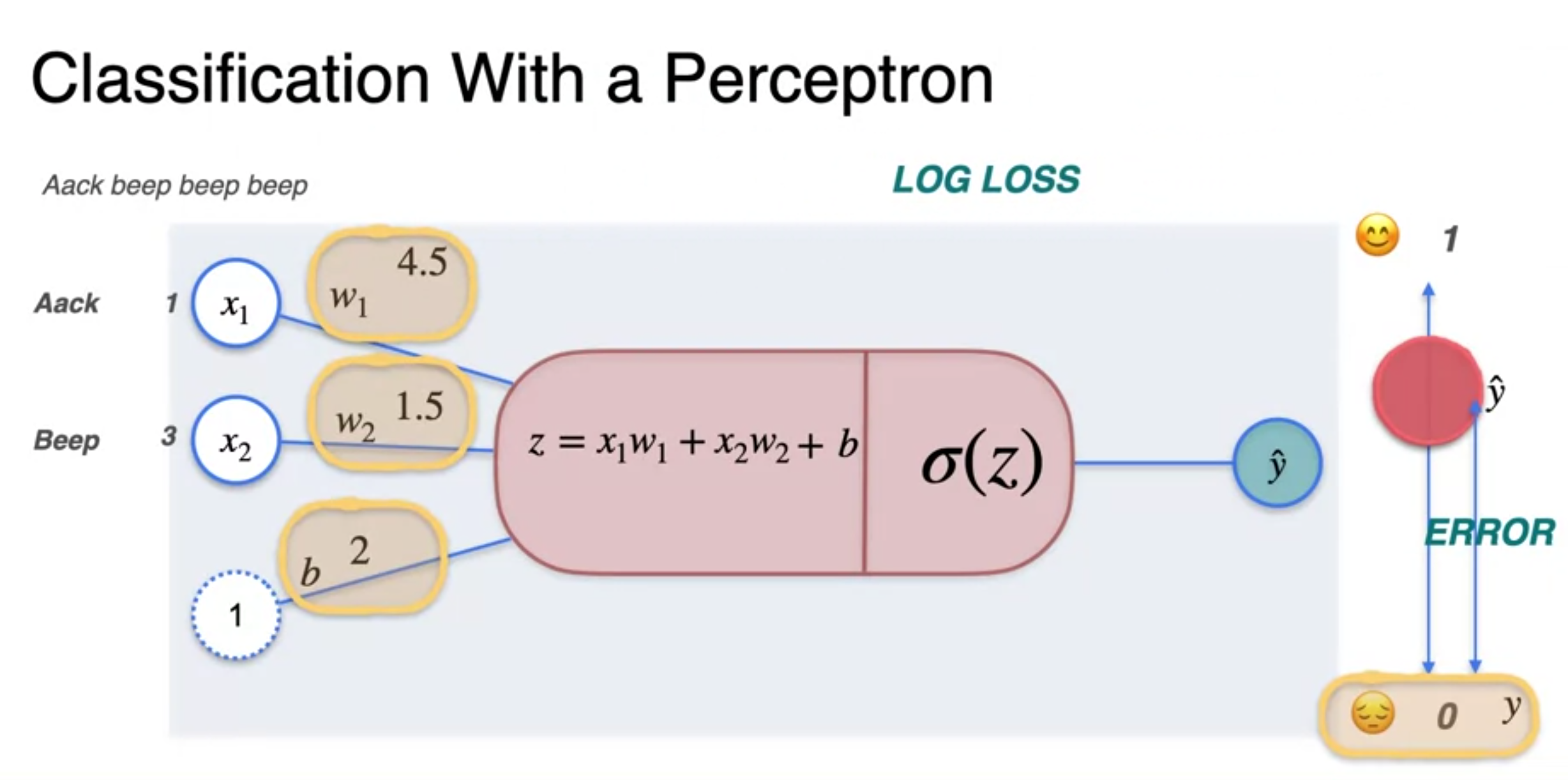
• To get the least log loss(y, y-hat) error
• Gradient descent

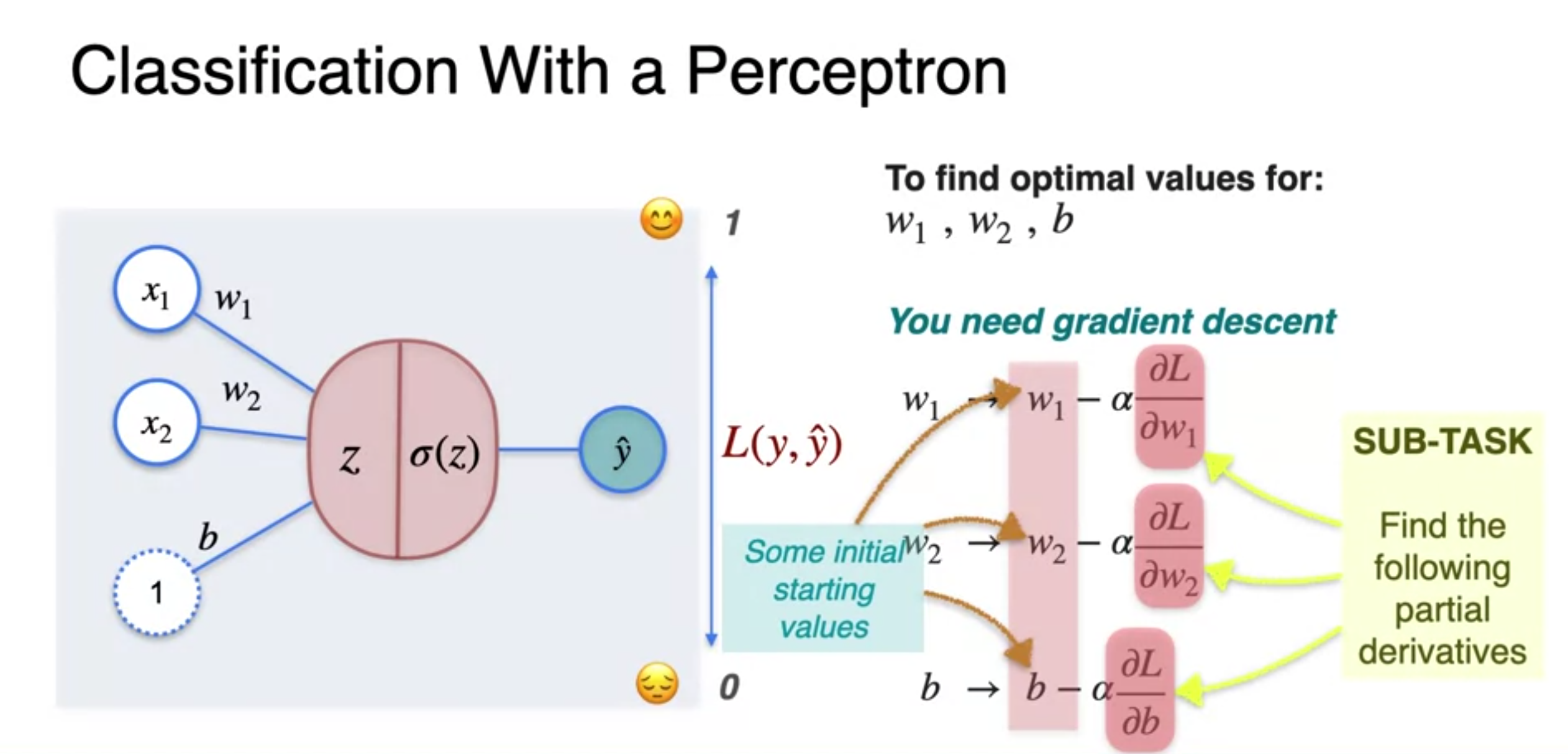
• Starts with arbitrary(random) values for weights and biases

Classification with a Neural Network

• Neural network : a bunch of perceptrons organized in layers

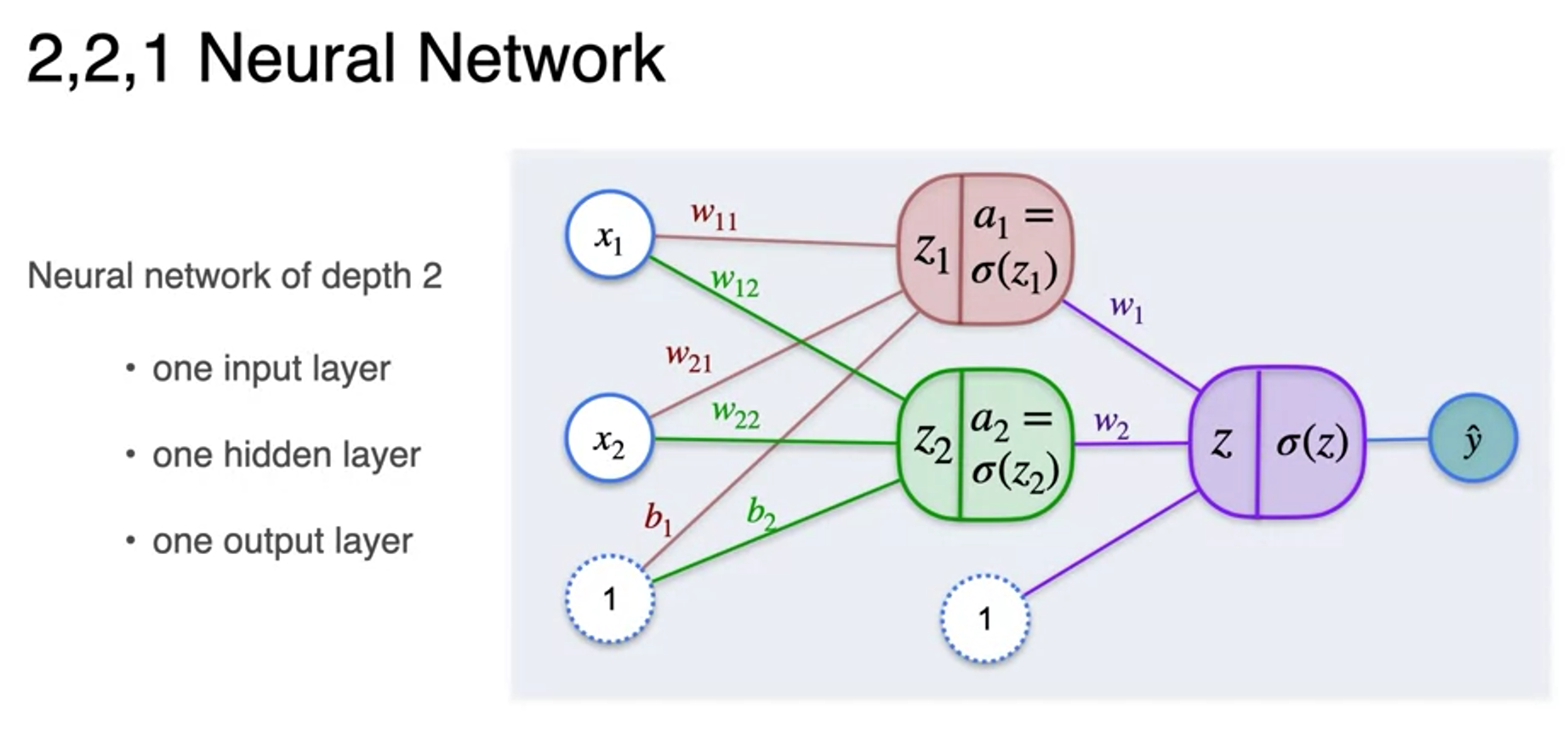
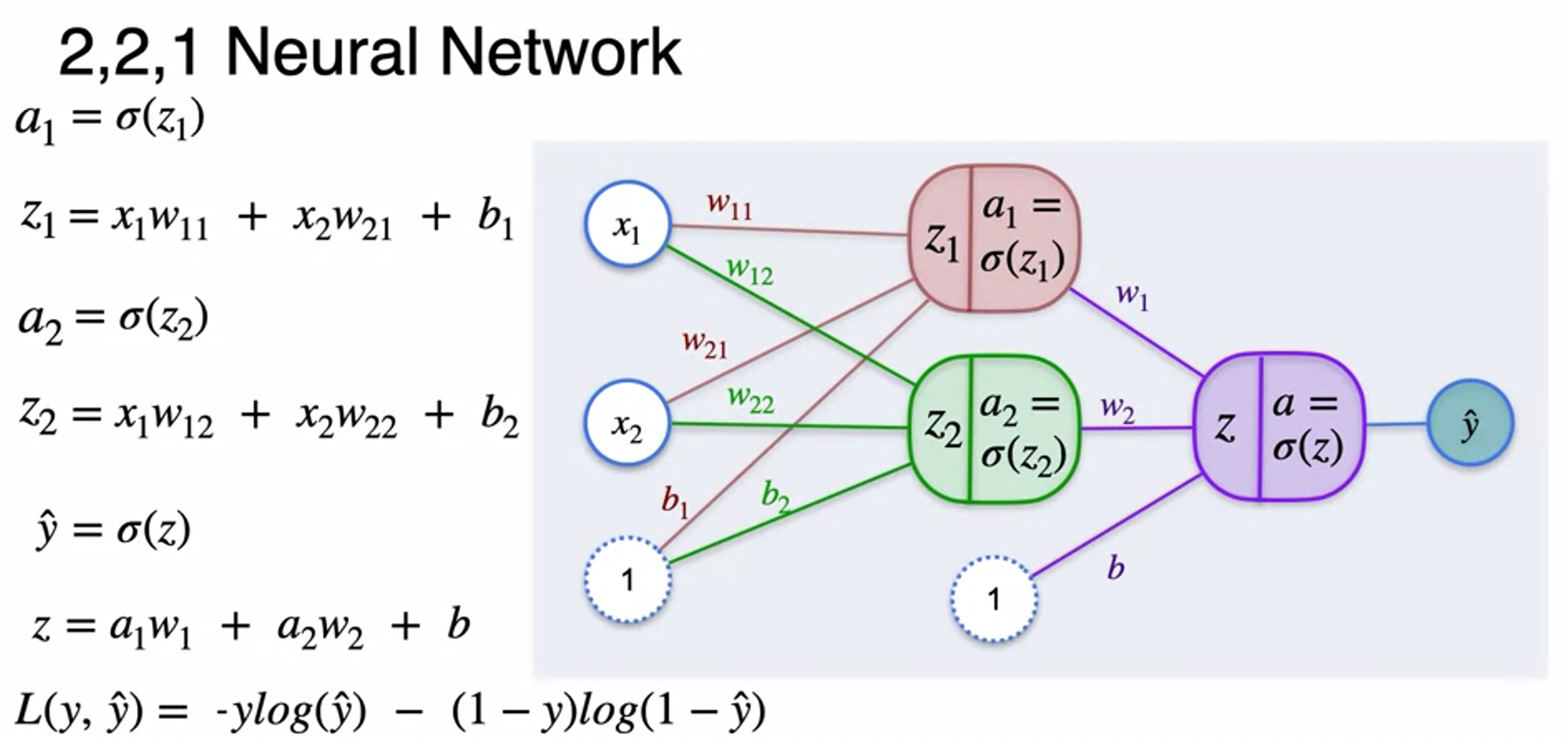
• How neural network calculated

Classification with a Neural Network - Minimizing log-loss

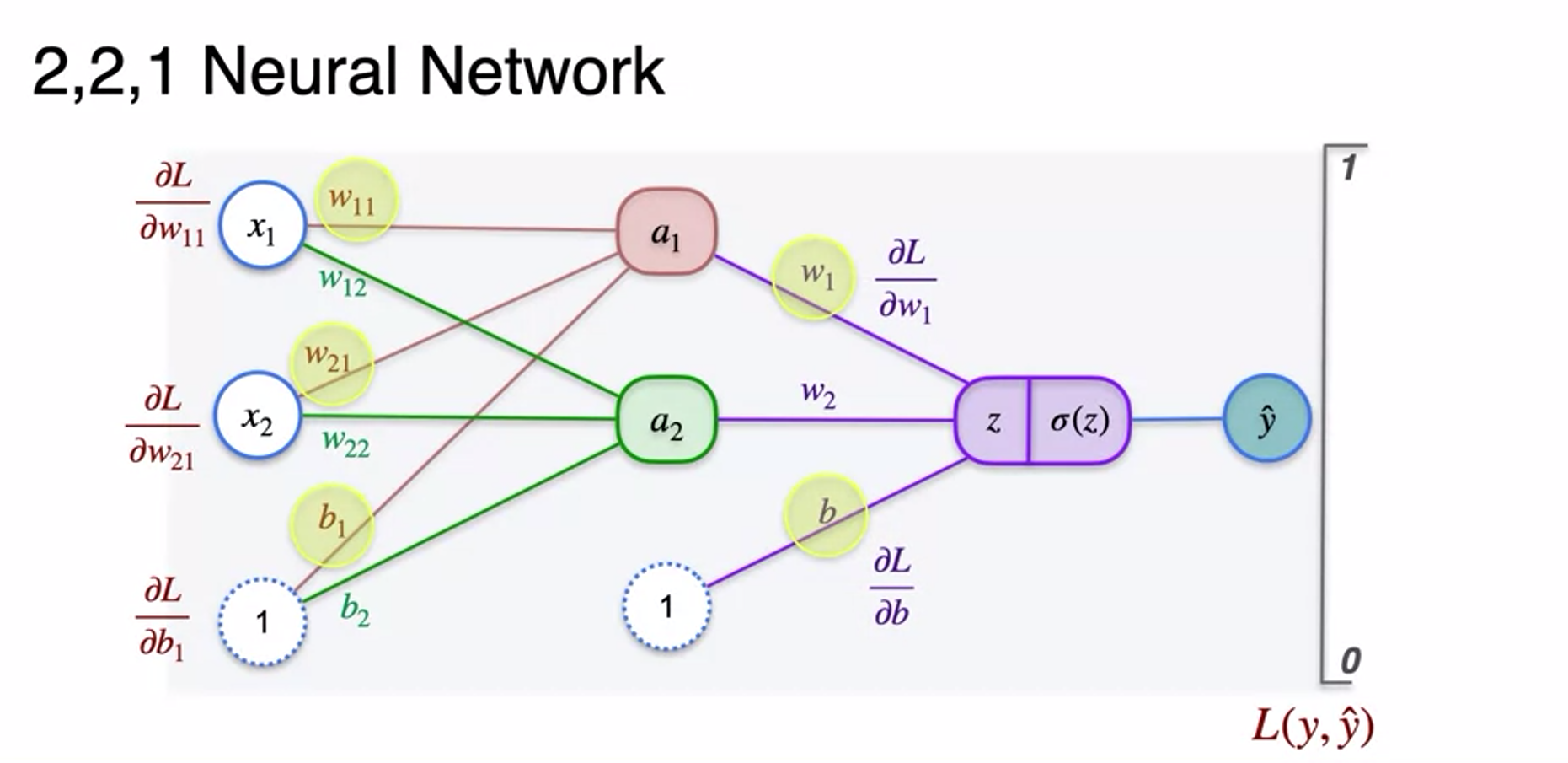
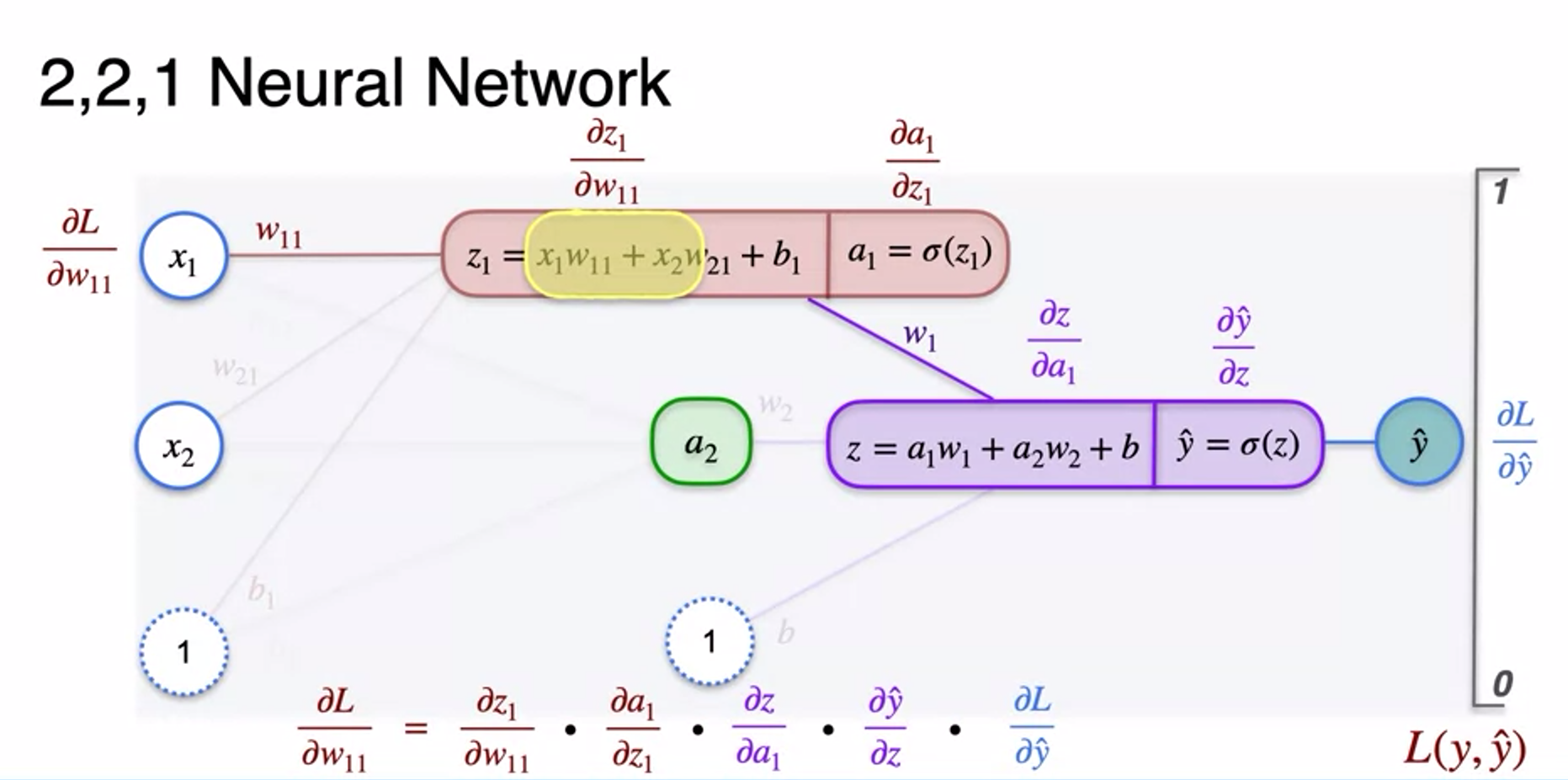
• how to update hidden weight to minimize log-logss

• so as bias

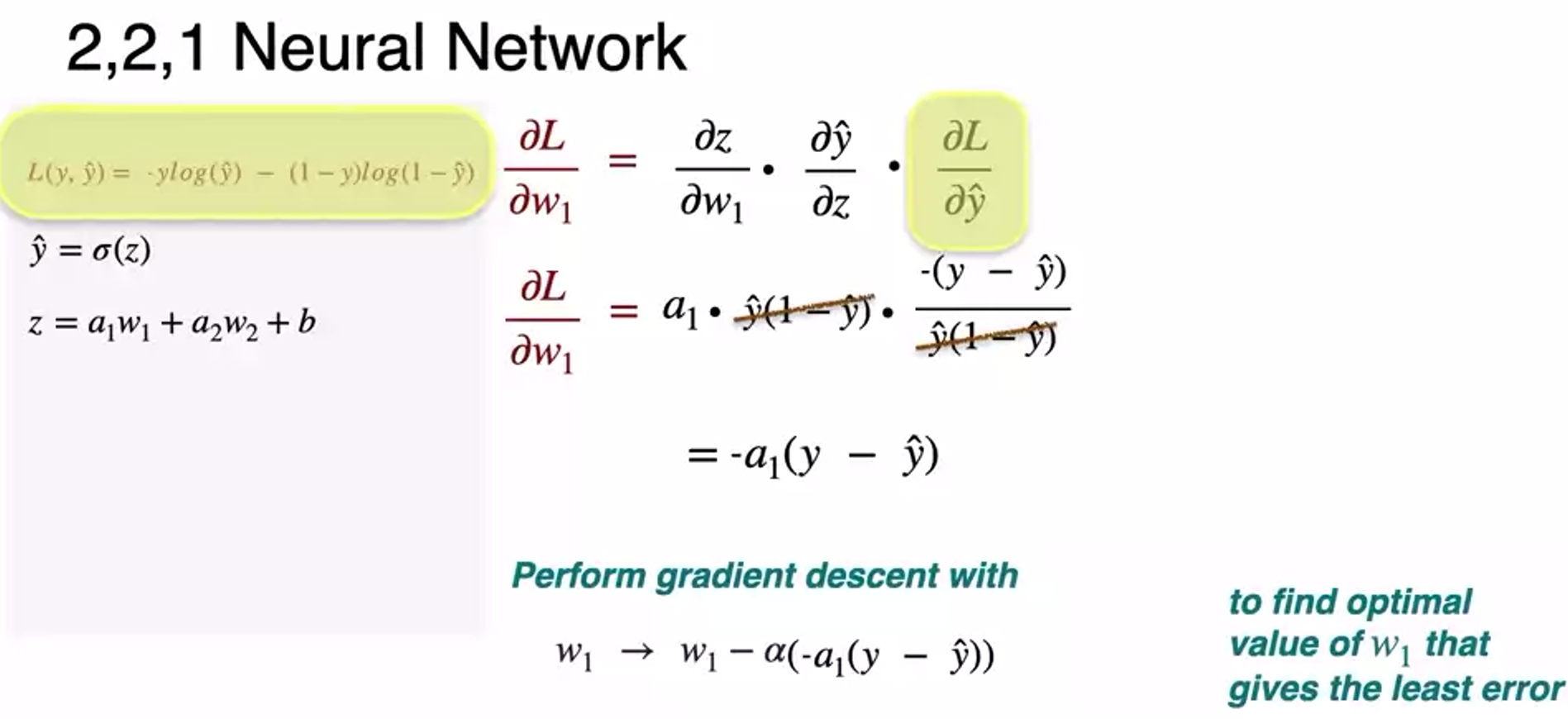
• so as weight

Gradient Descent and Backpropagation

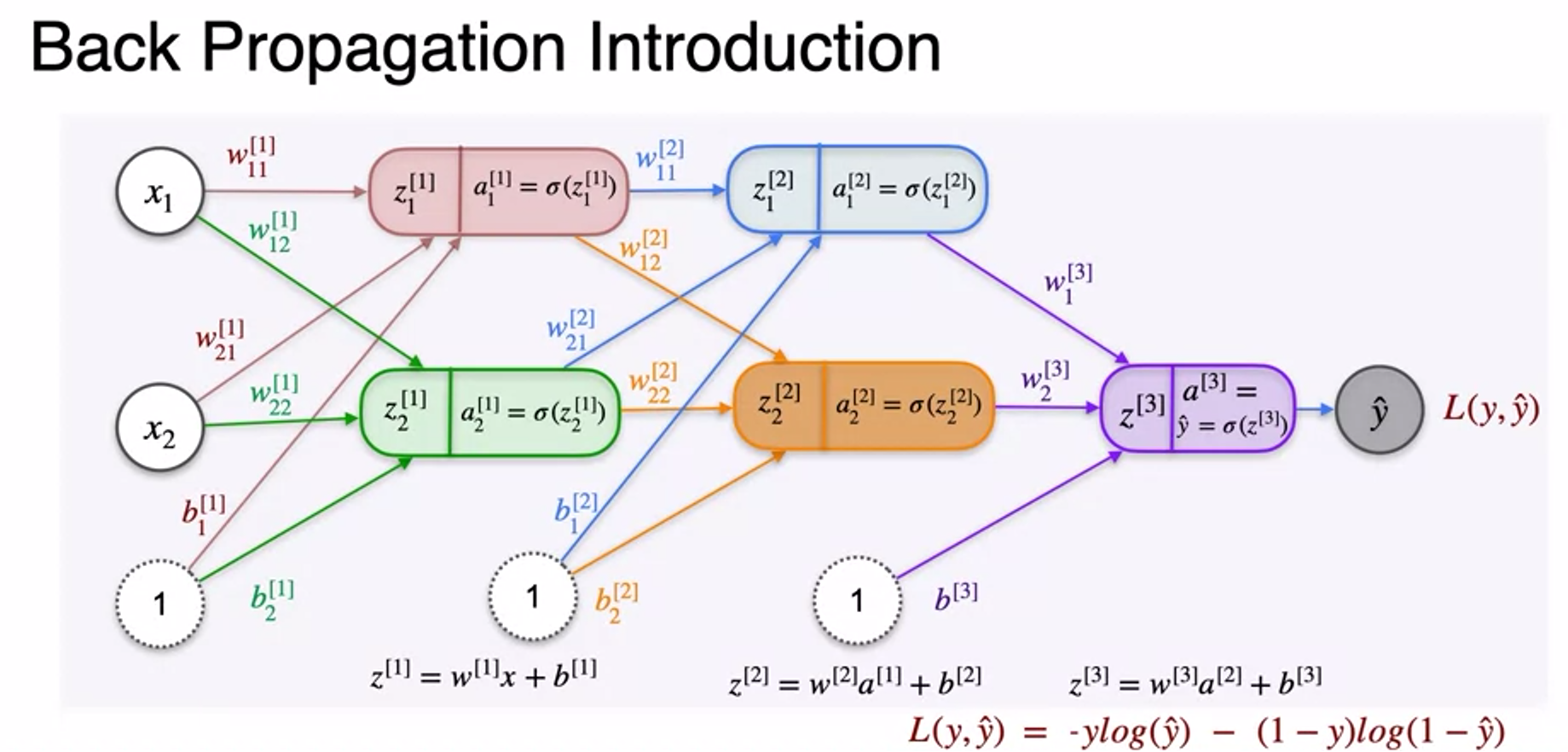
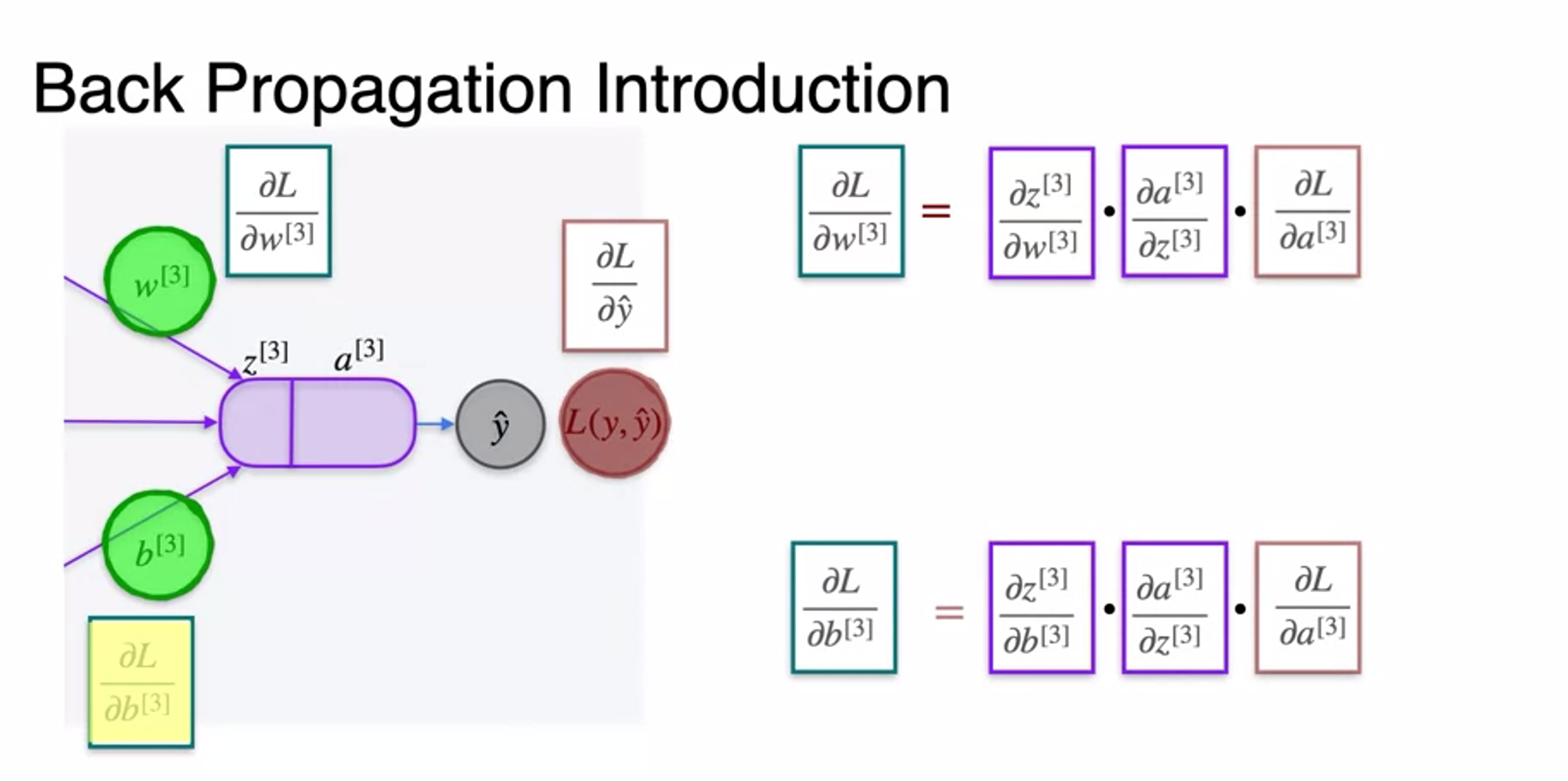
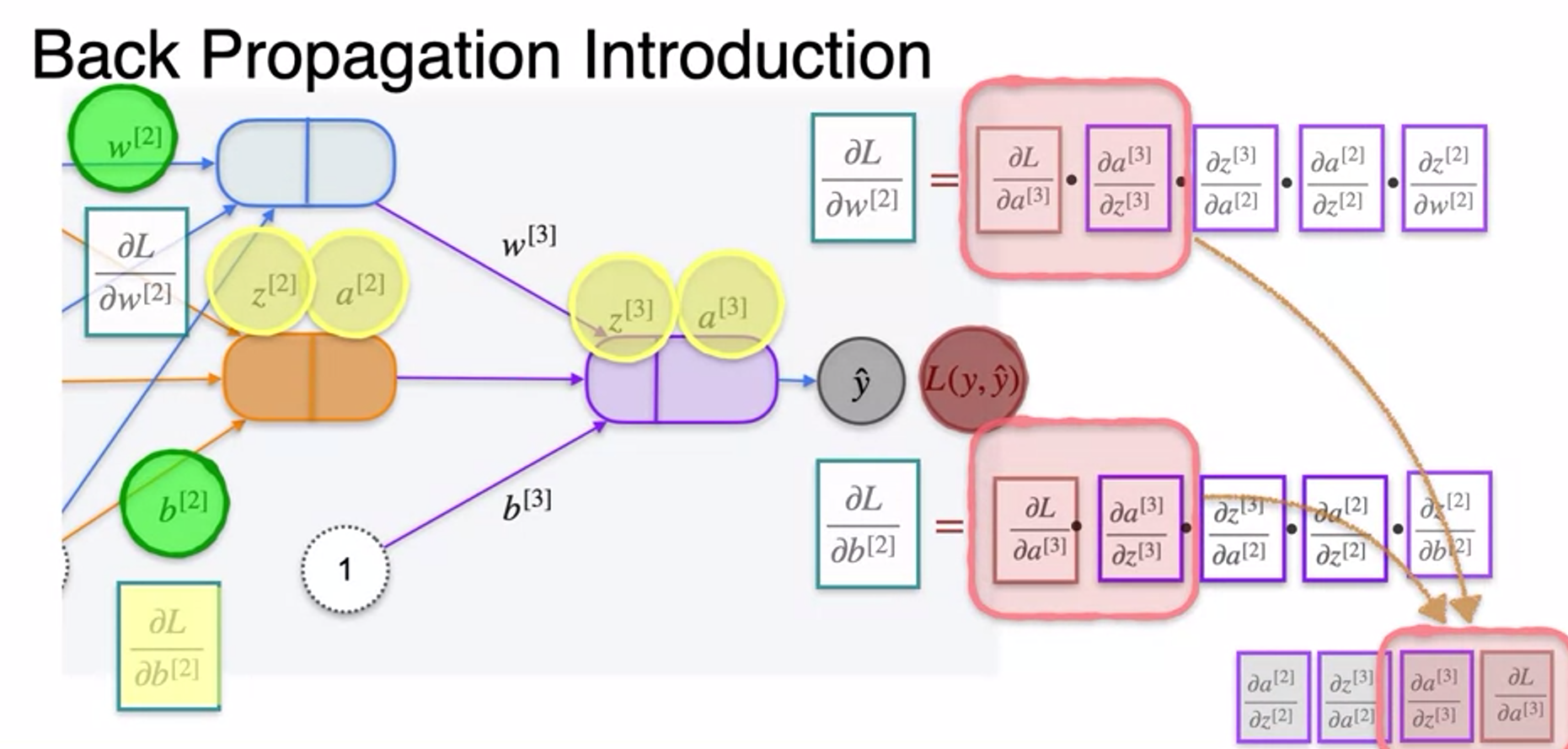
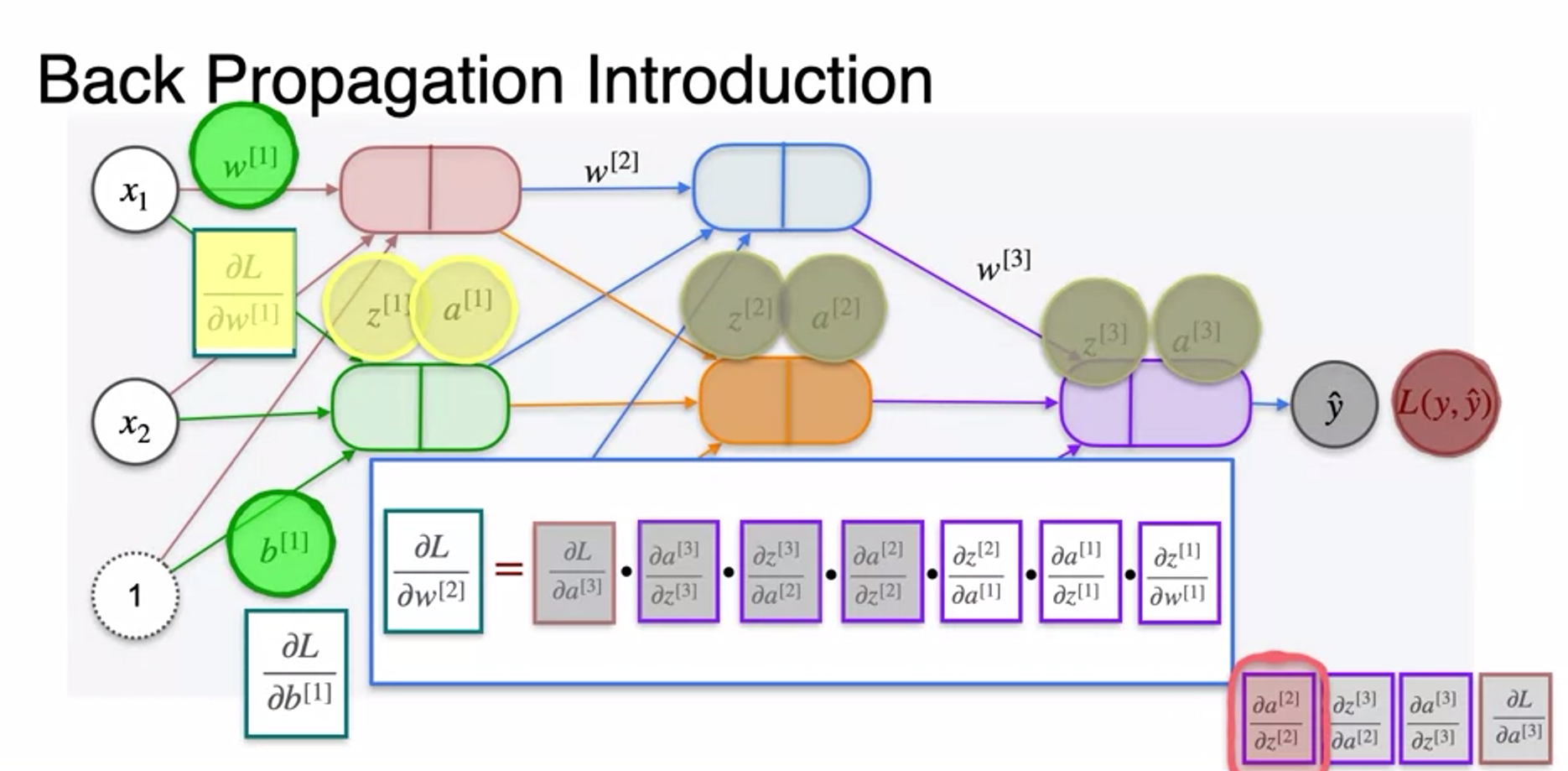
• very long chain rule

Newton's Method

Newton's Method

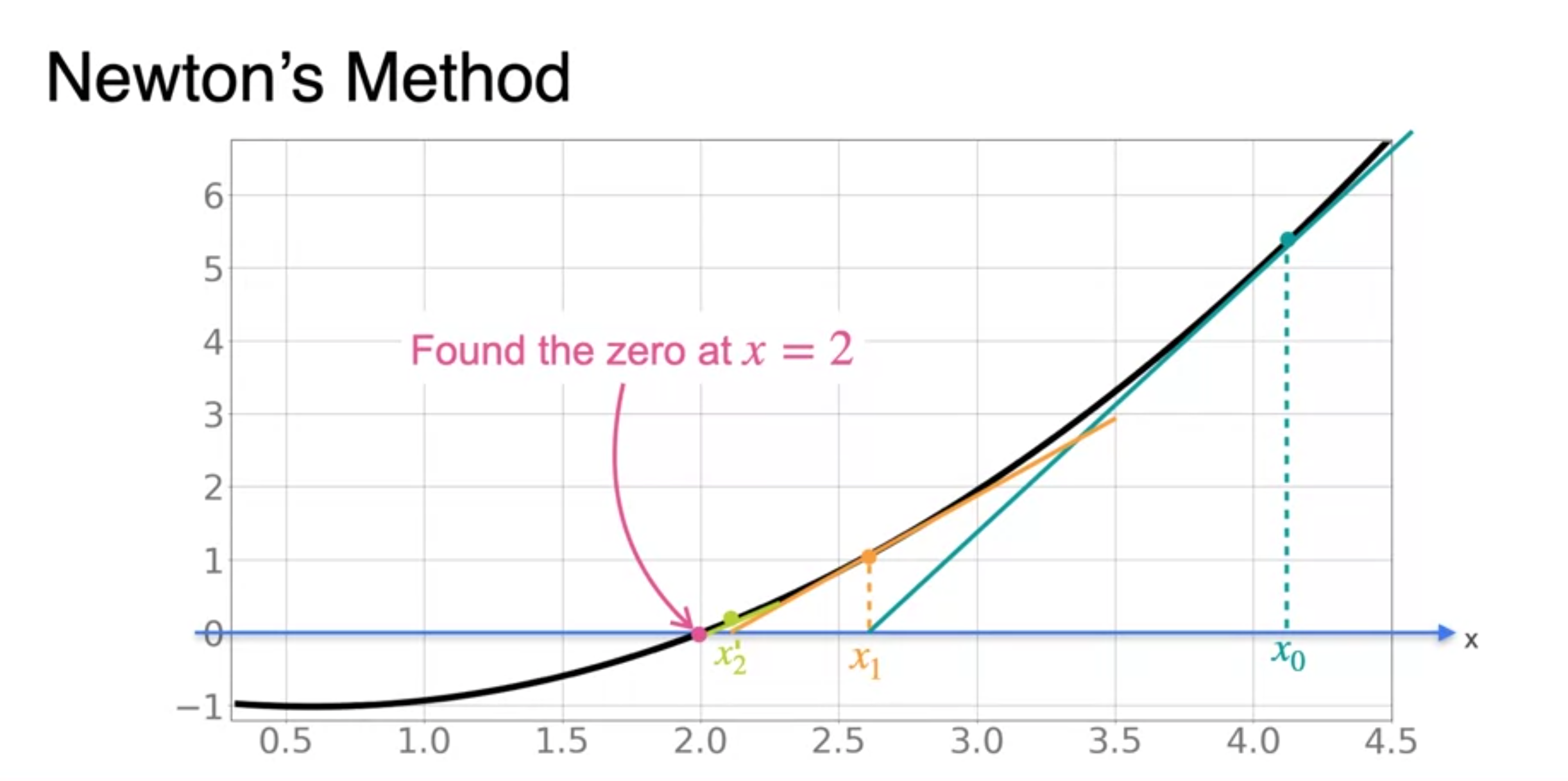
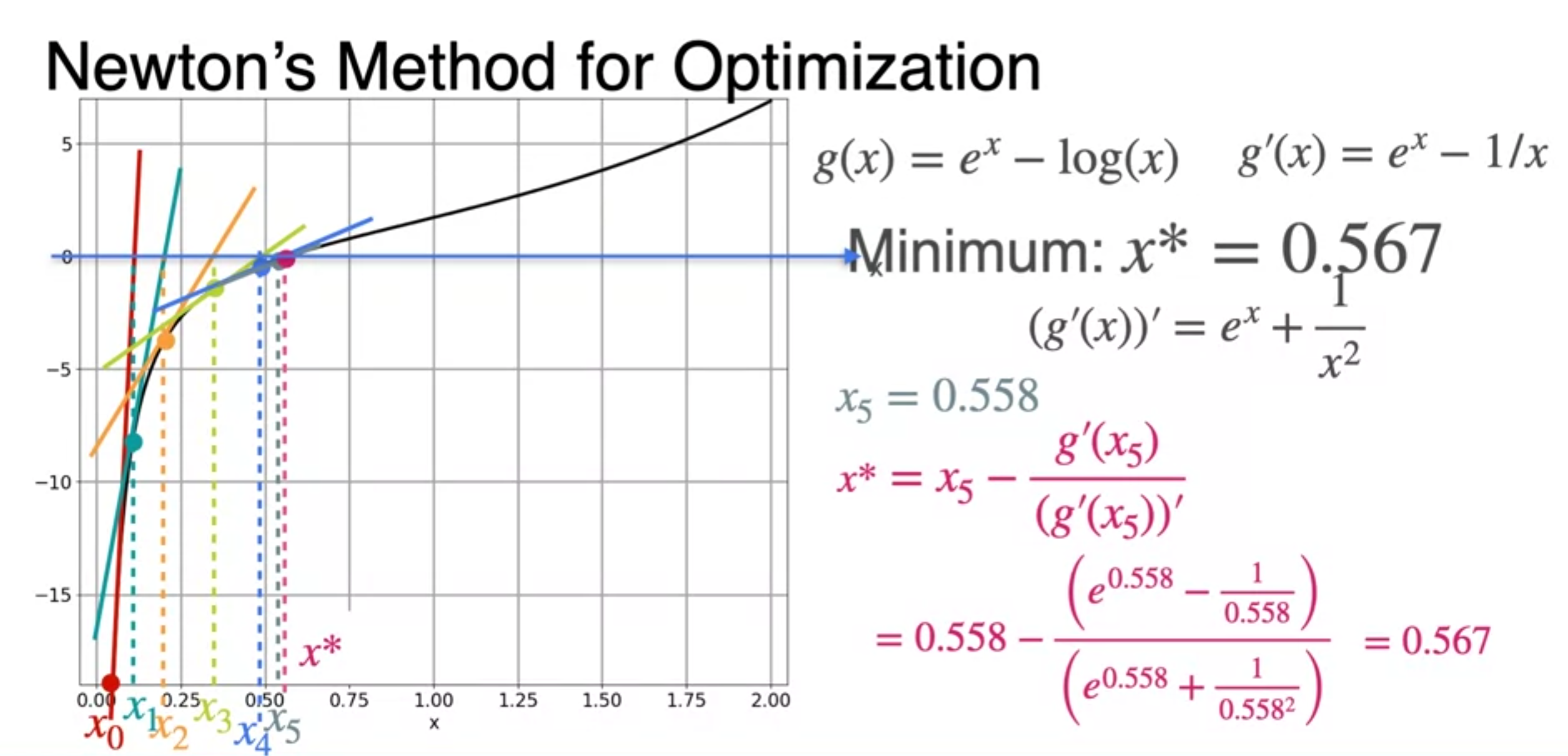
Newton's Method: An example

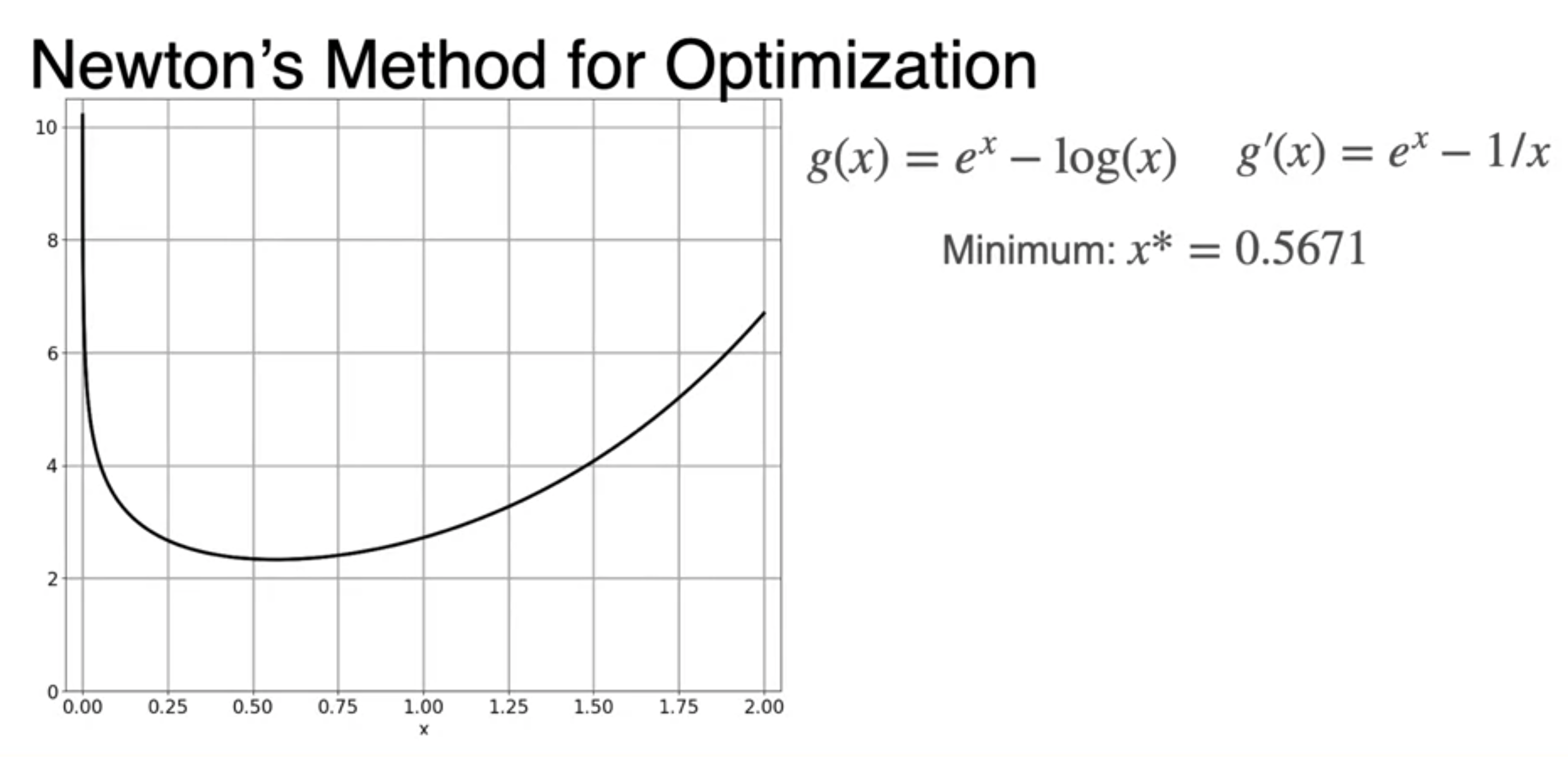
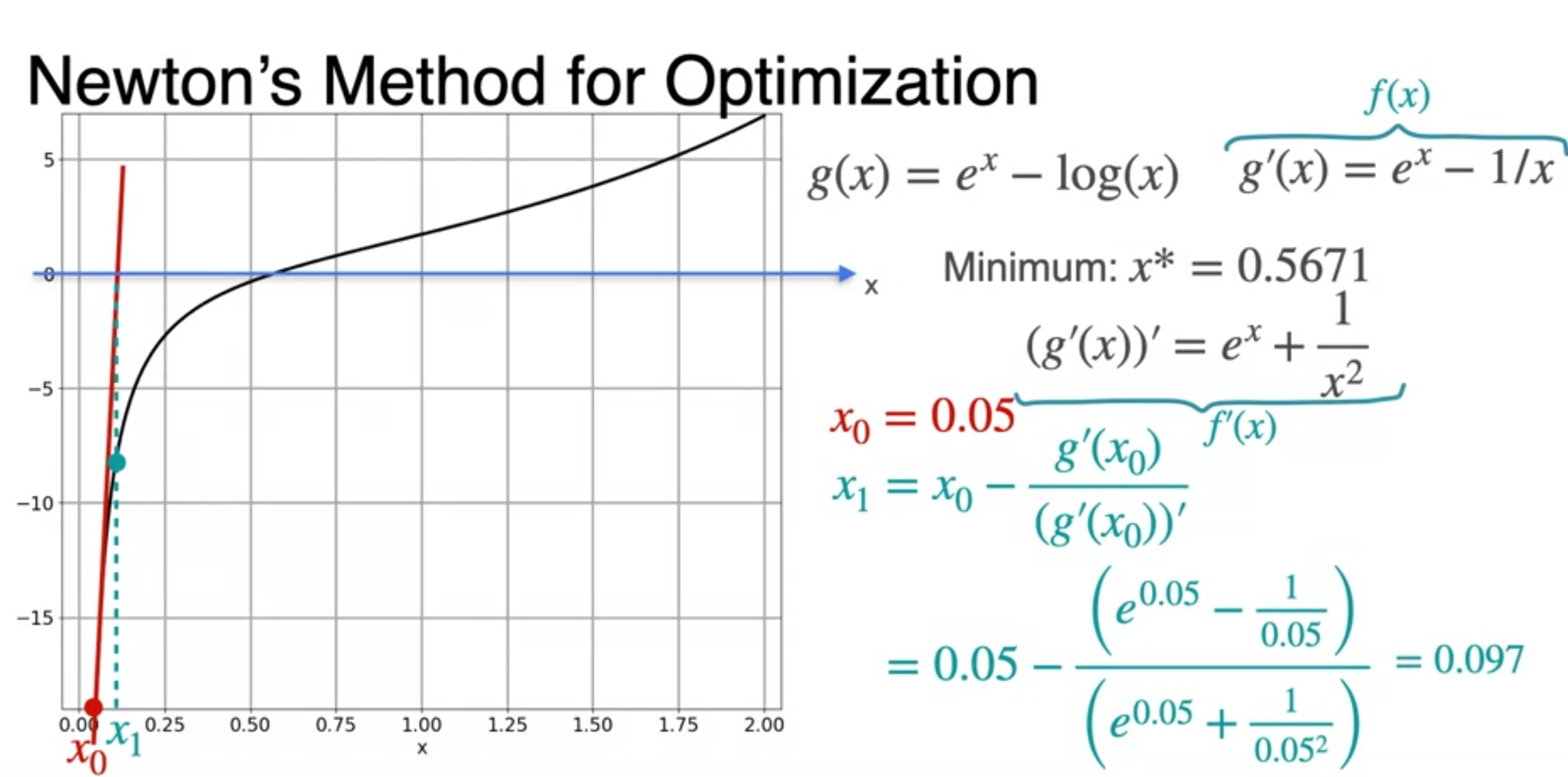
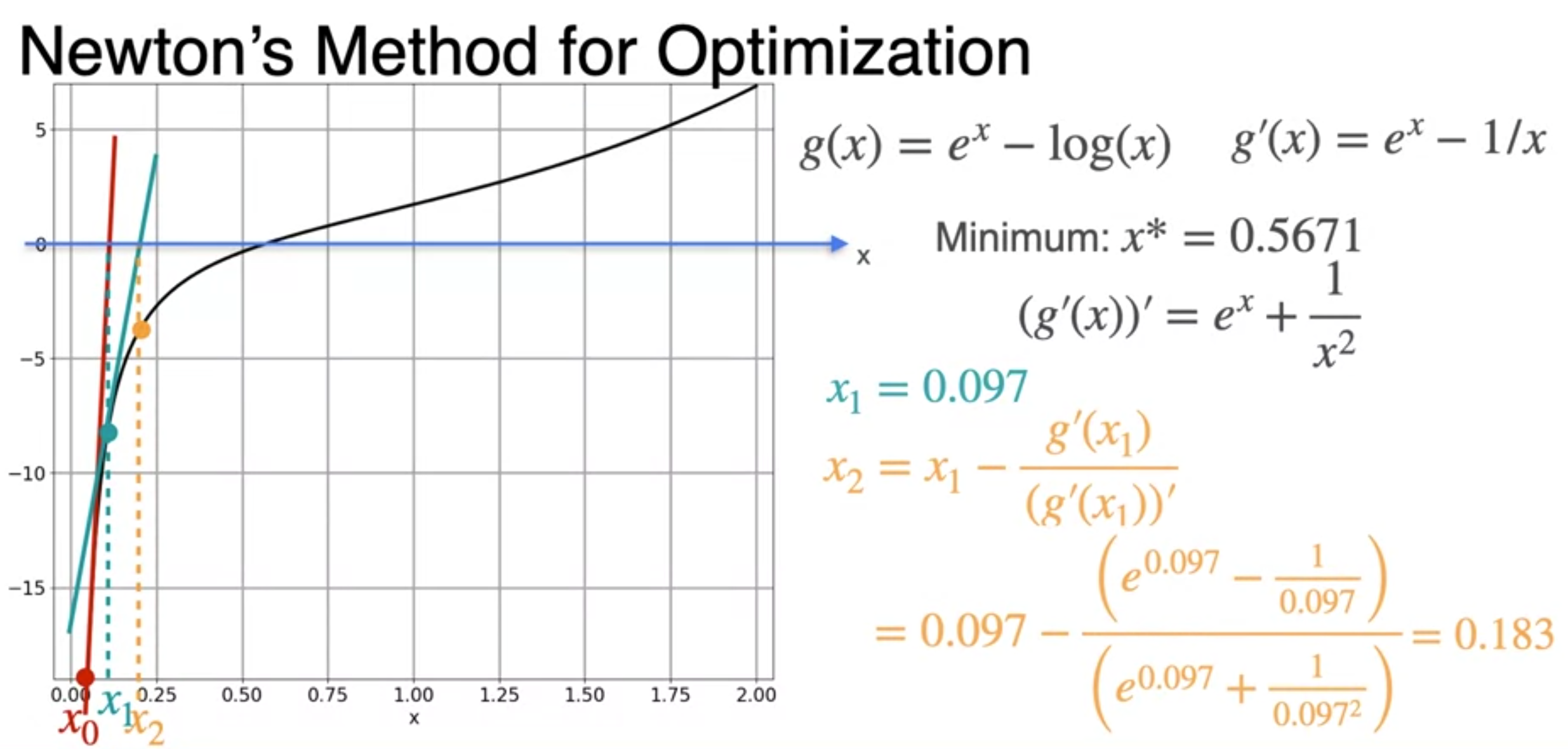
• repeat to the minimum

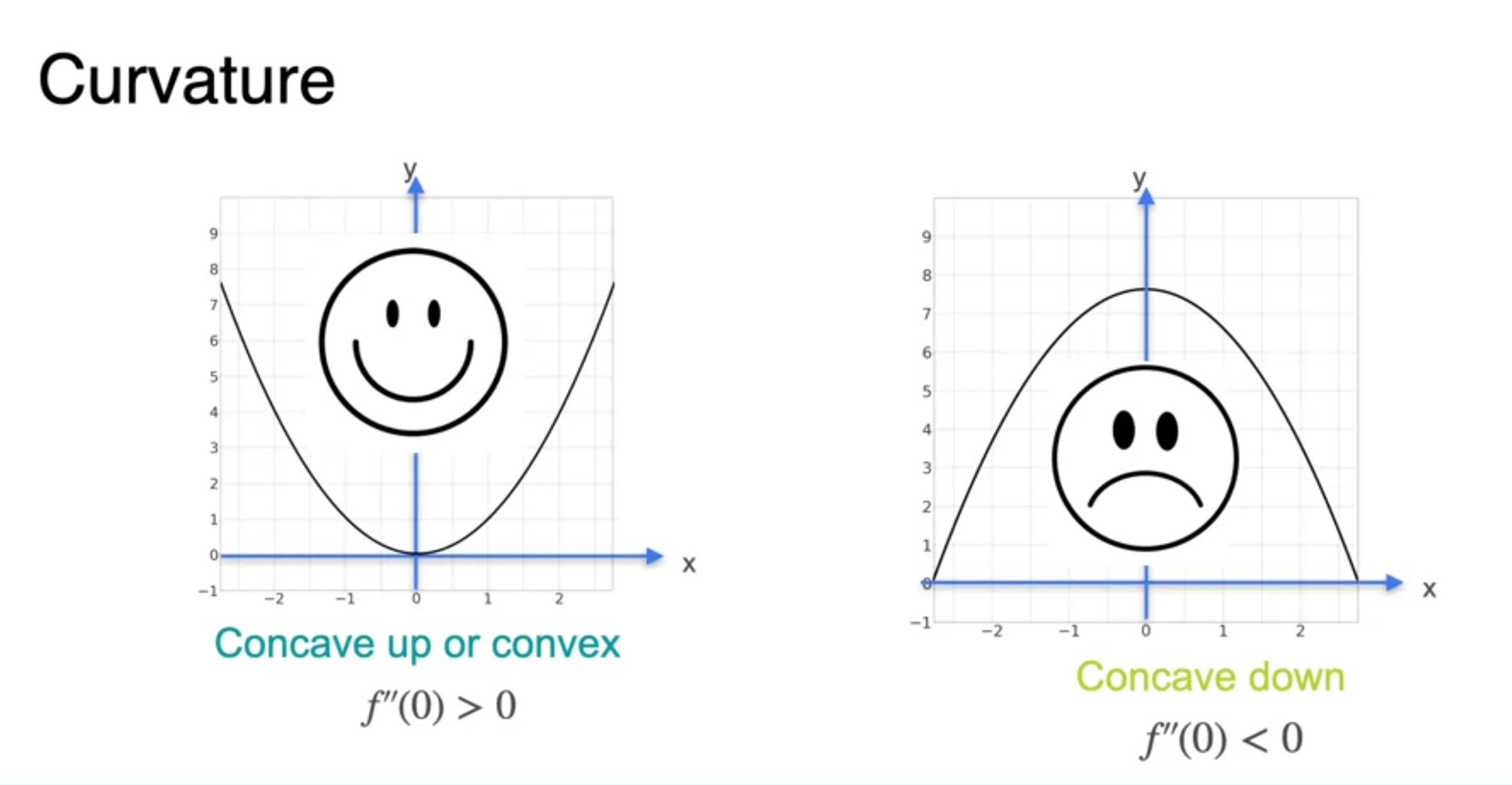
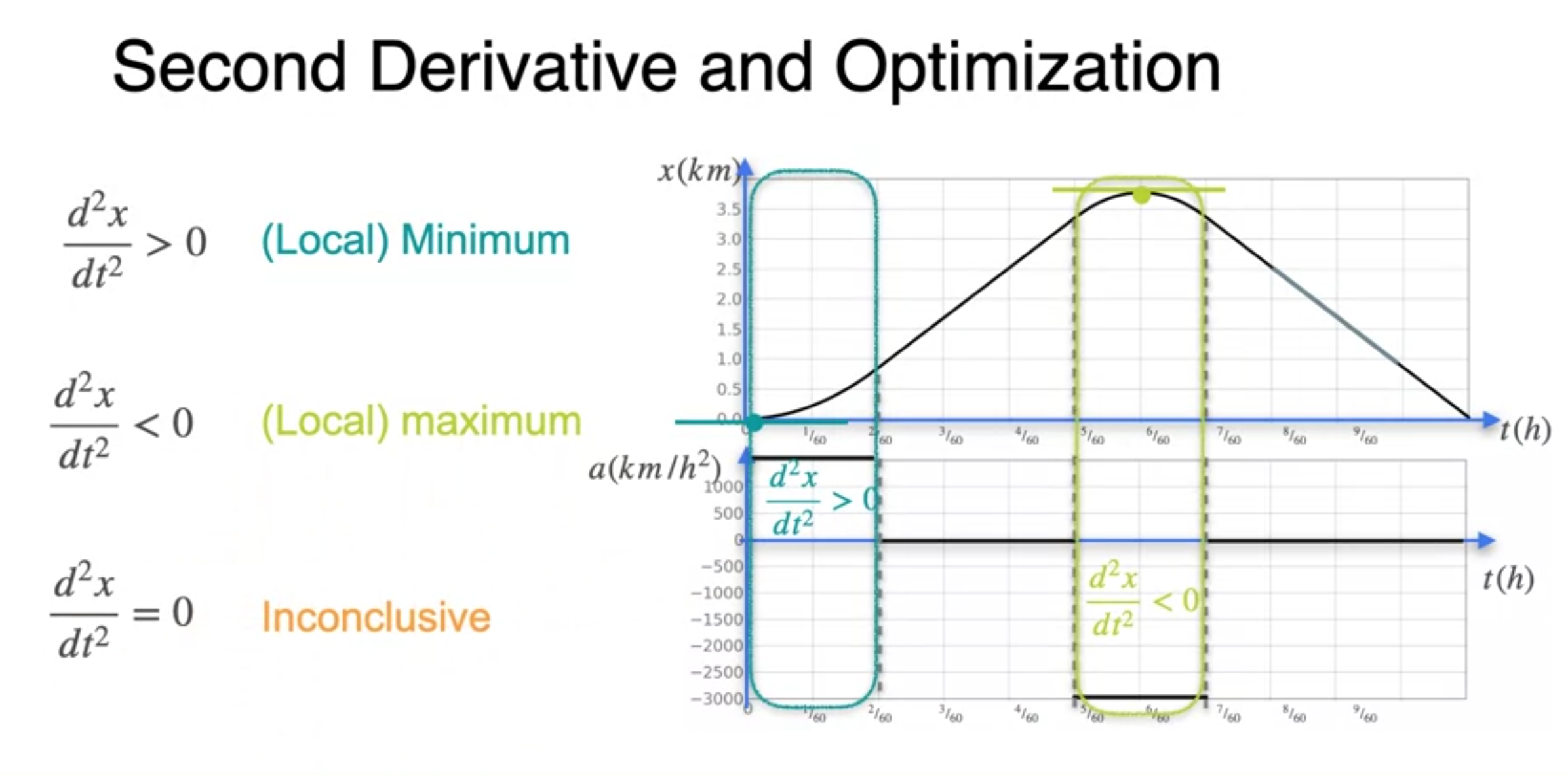
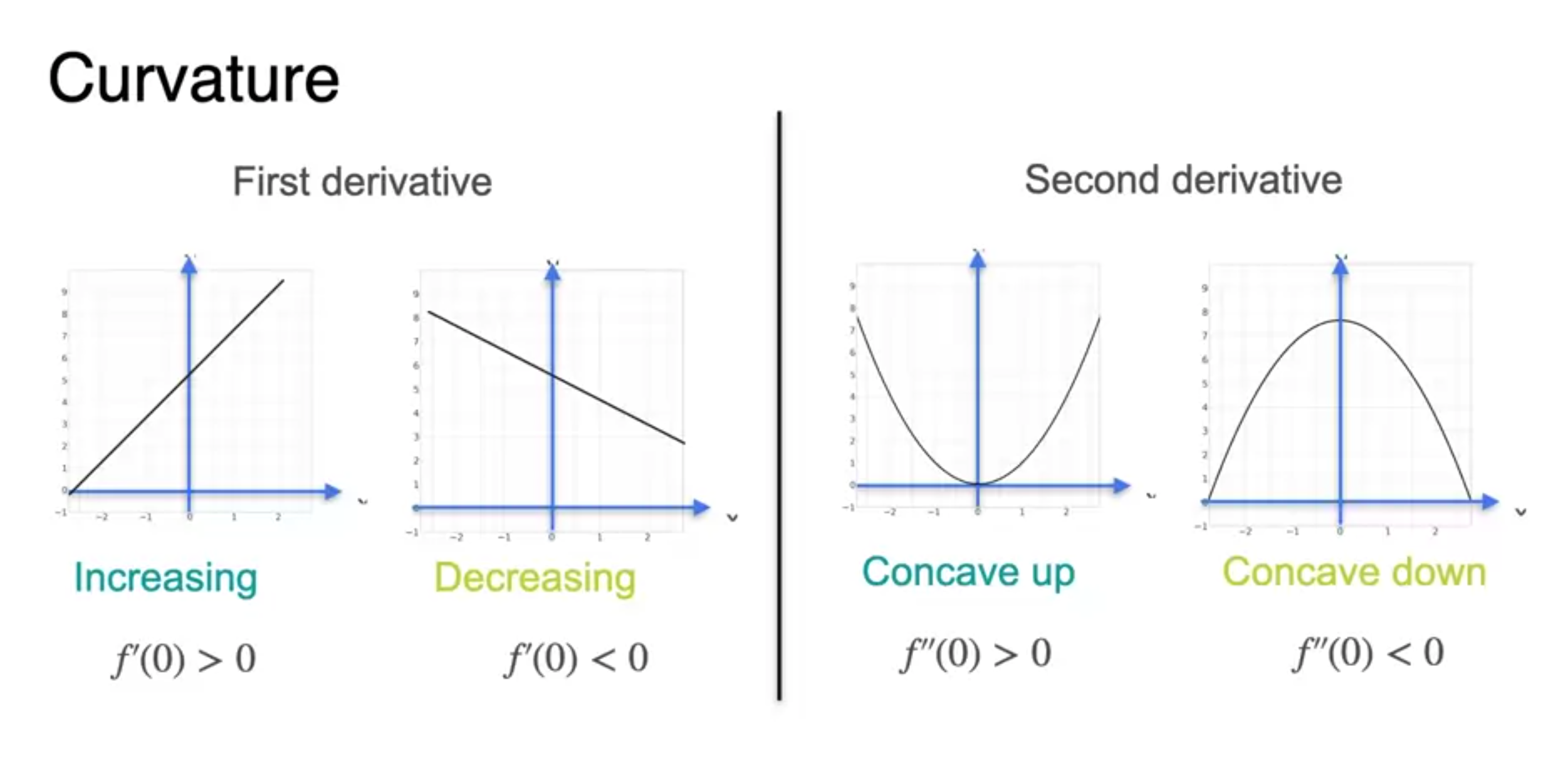
The second derivative

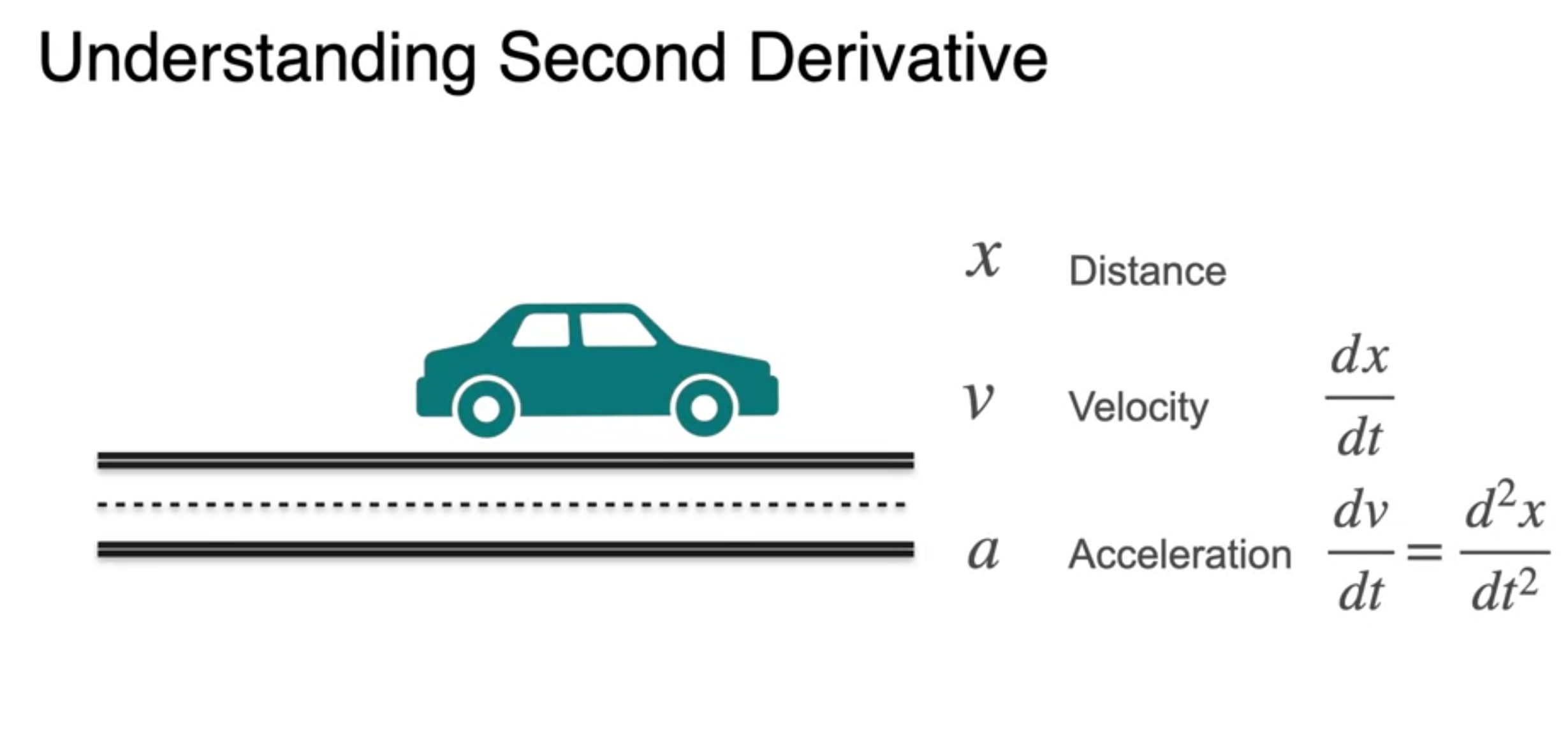
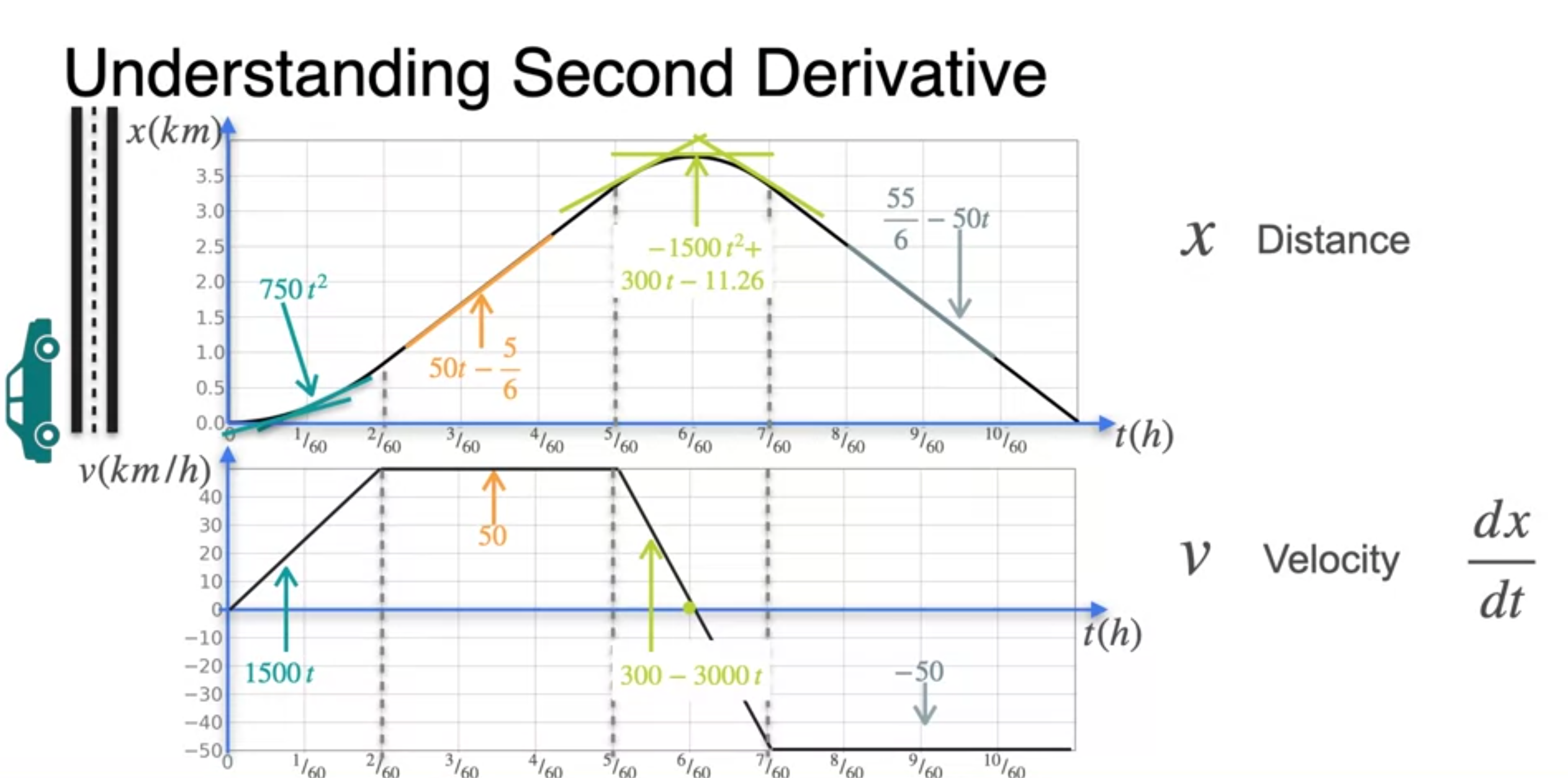
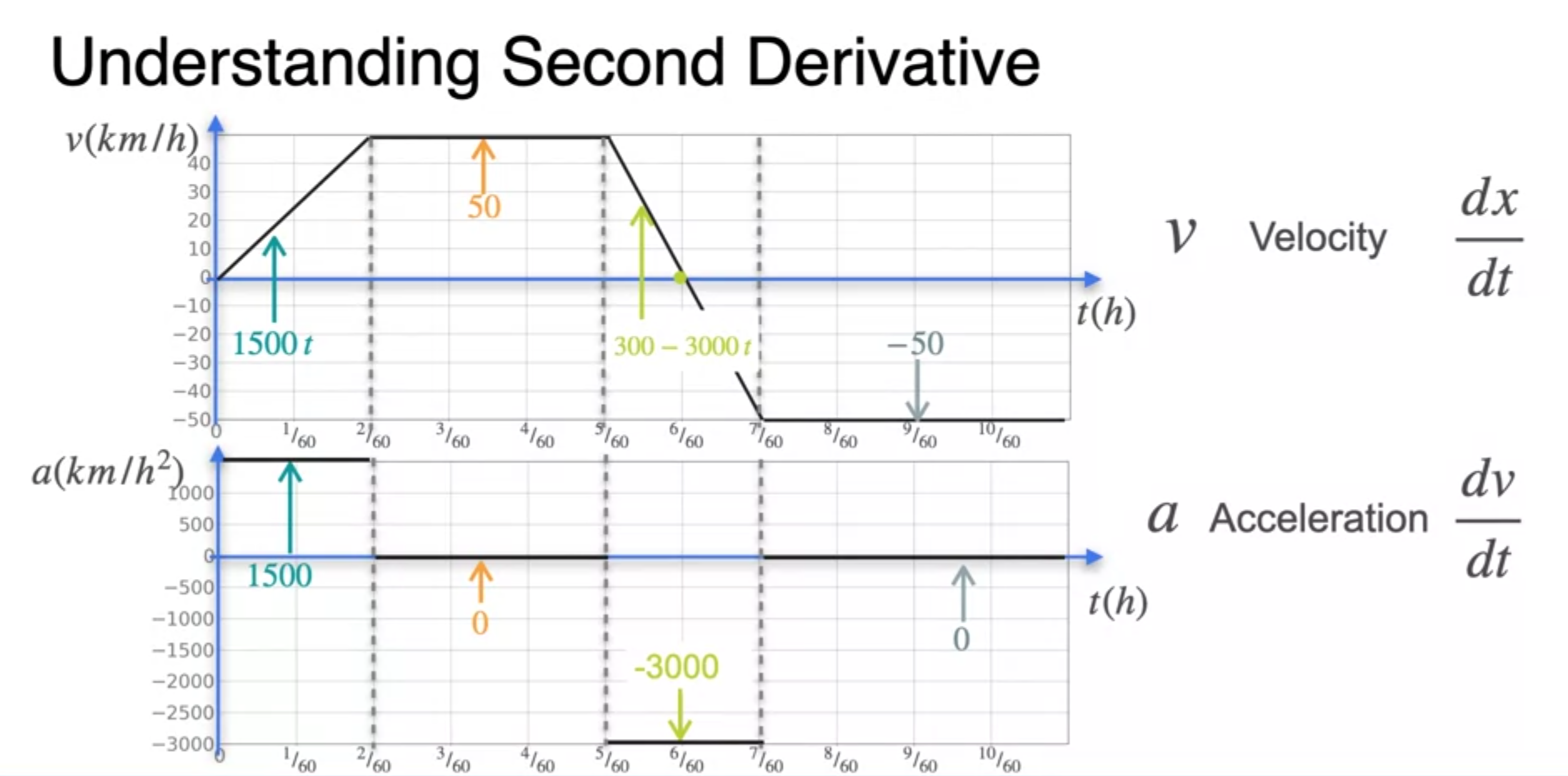
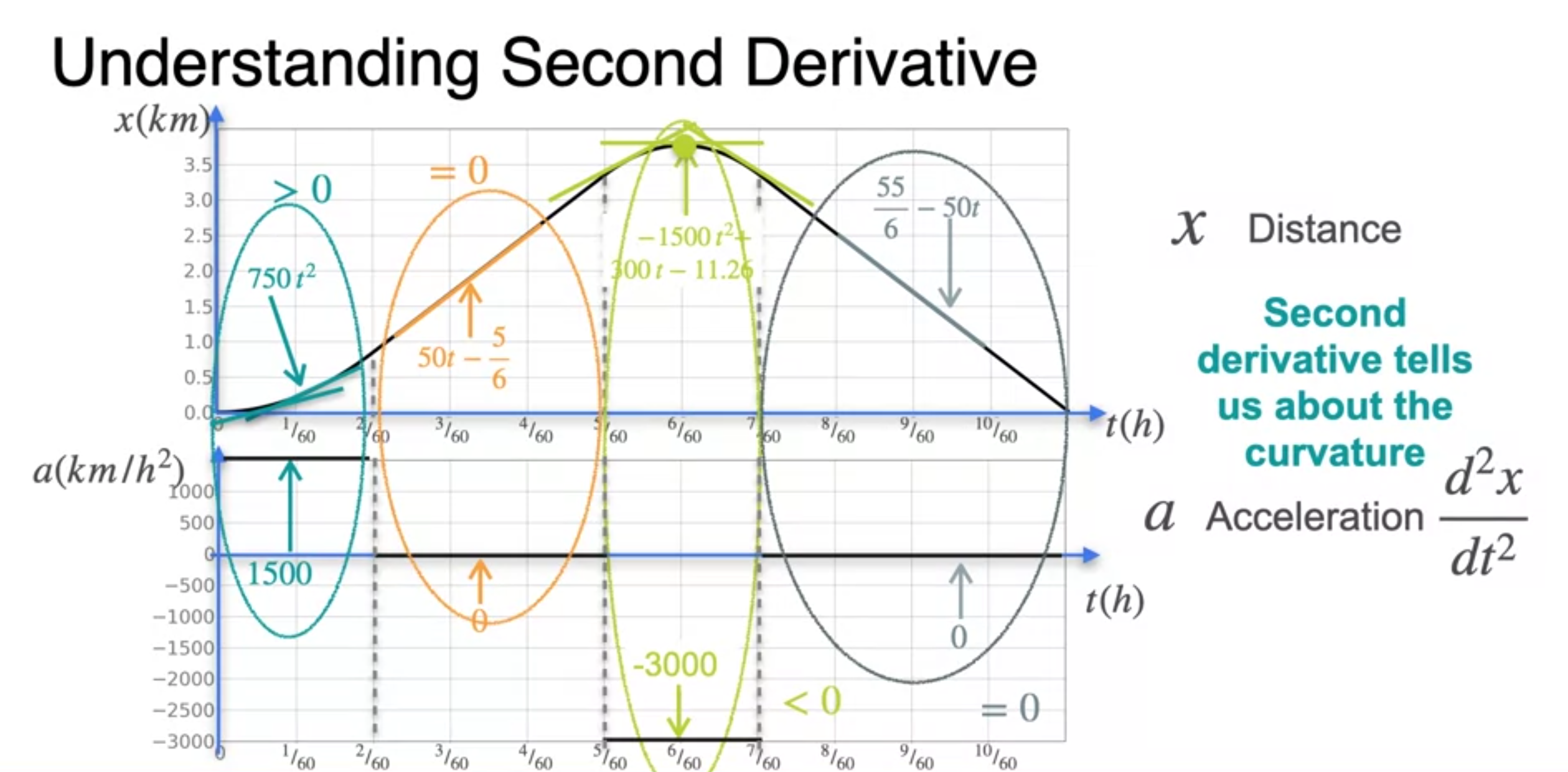
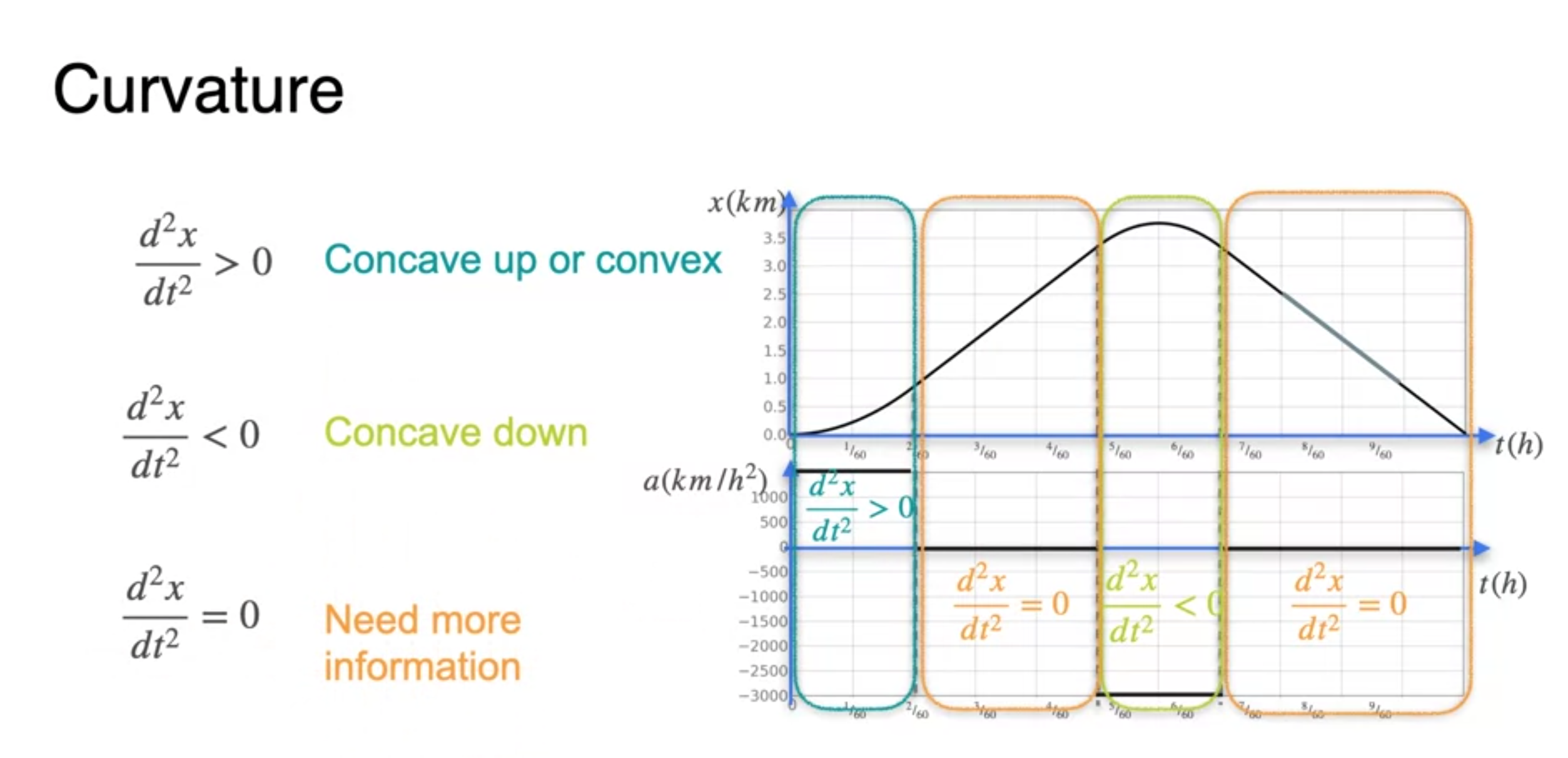
• Curvature(곡률)에 대한 이해

The Hessian

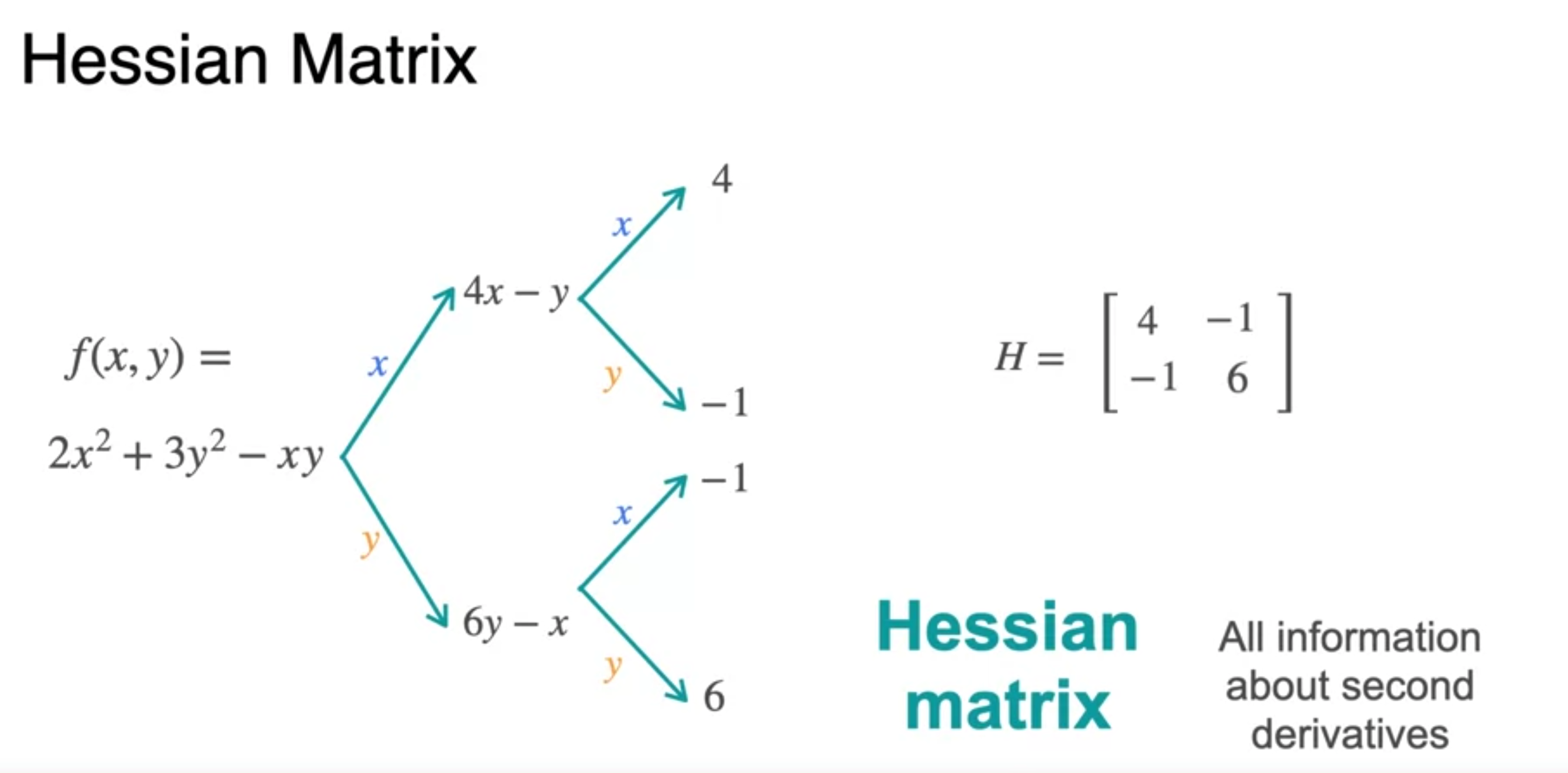
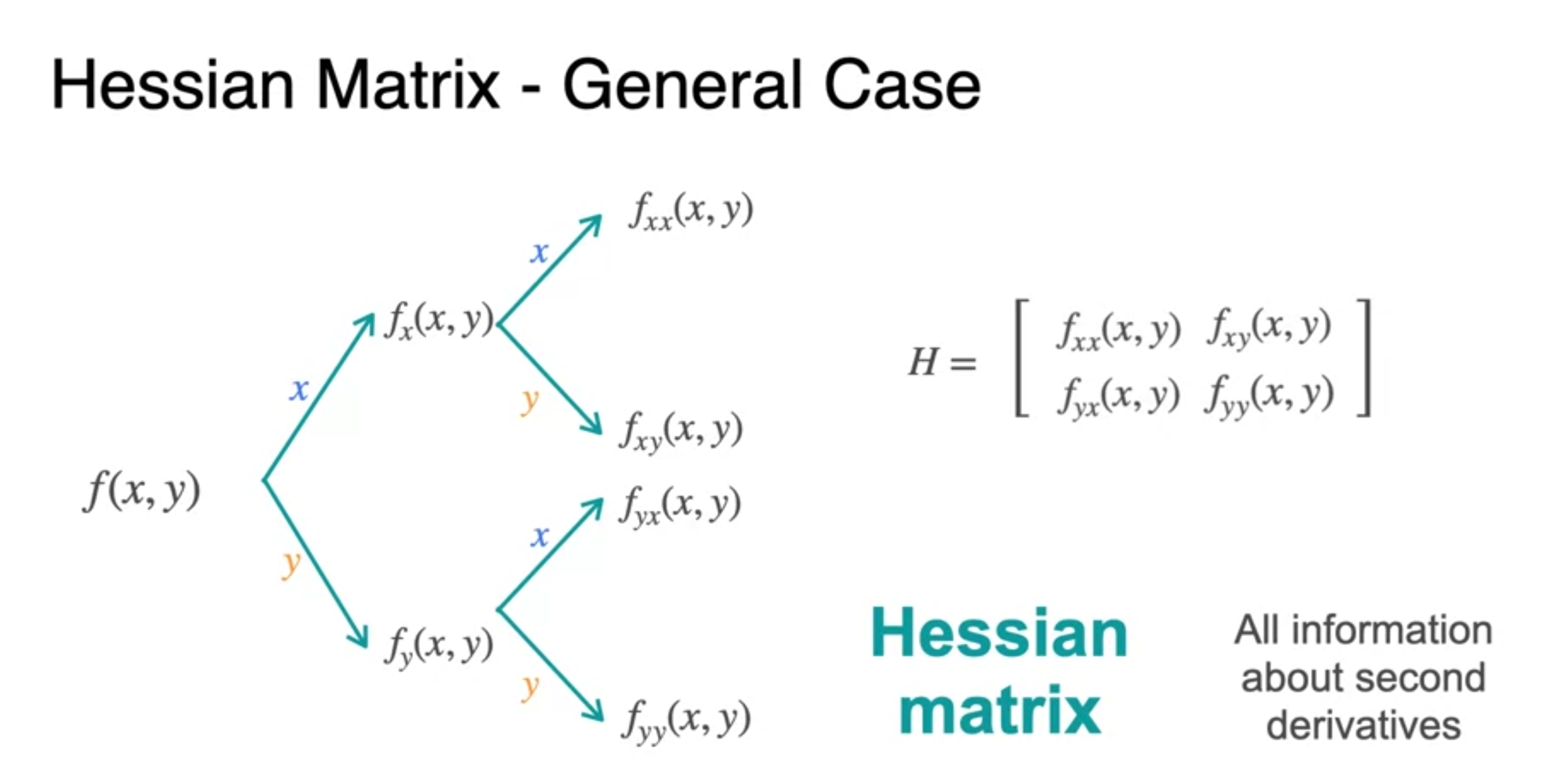
• Hessian은 symmetric하다

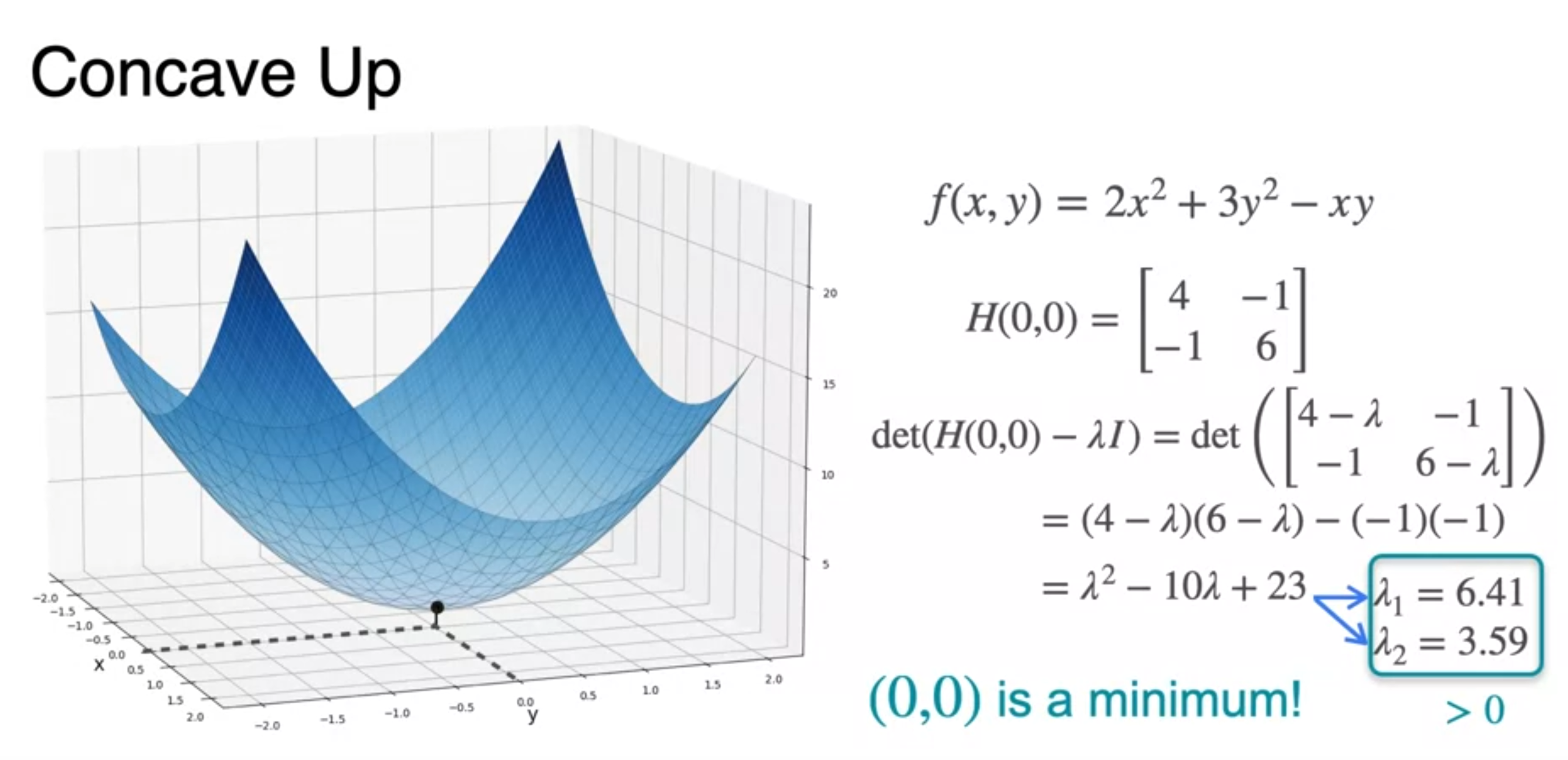
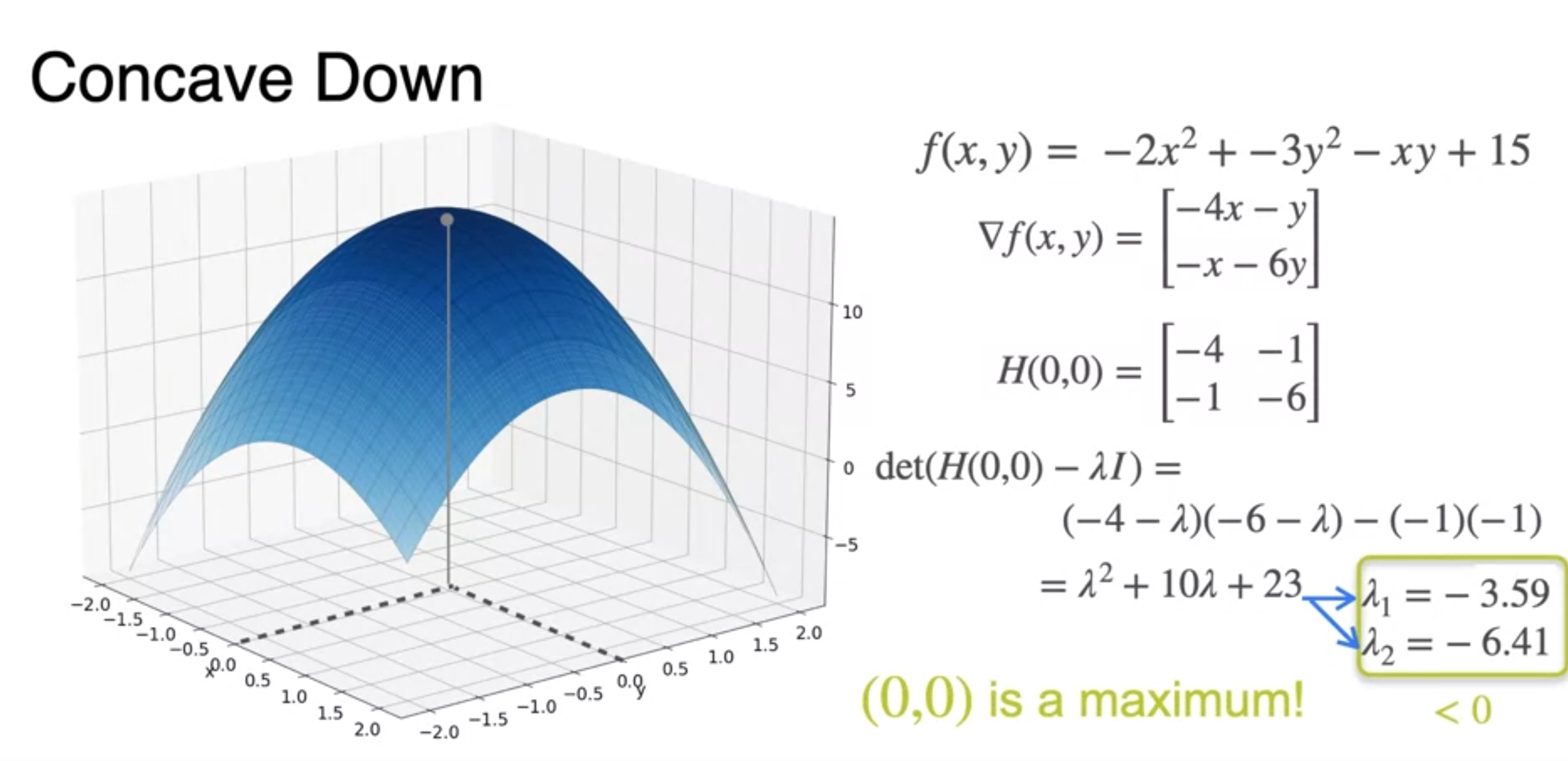
Hessians and concavity

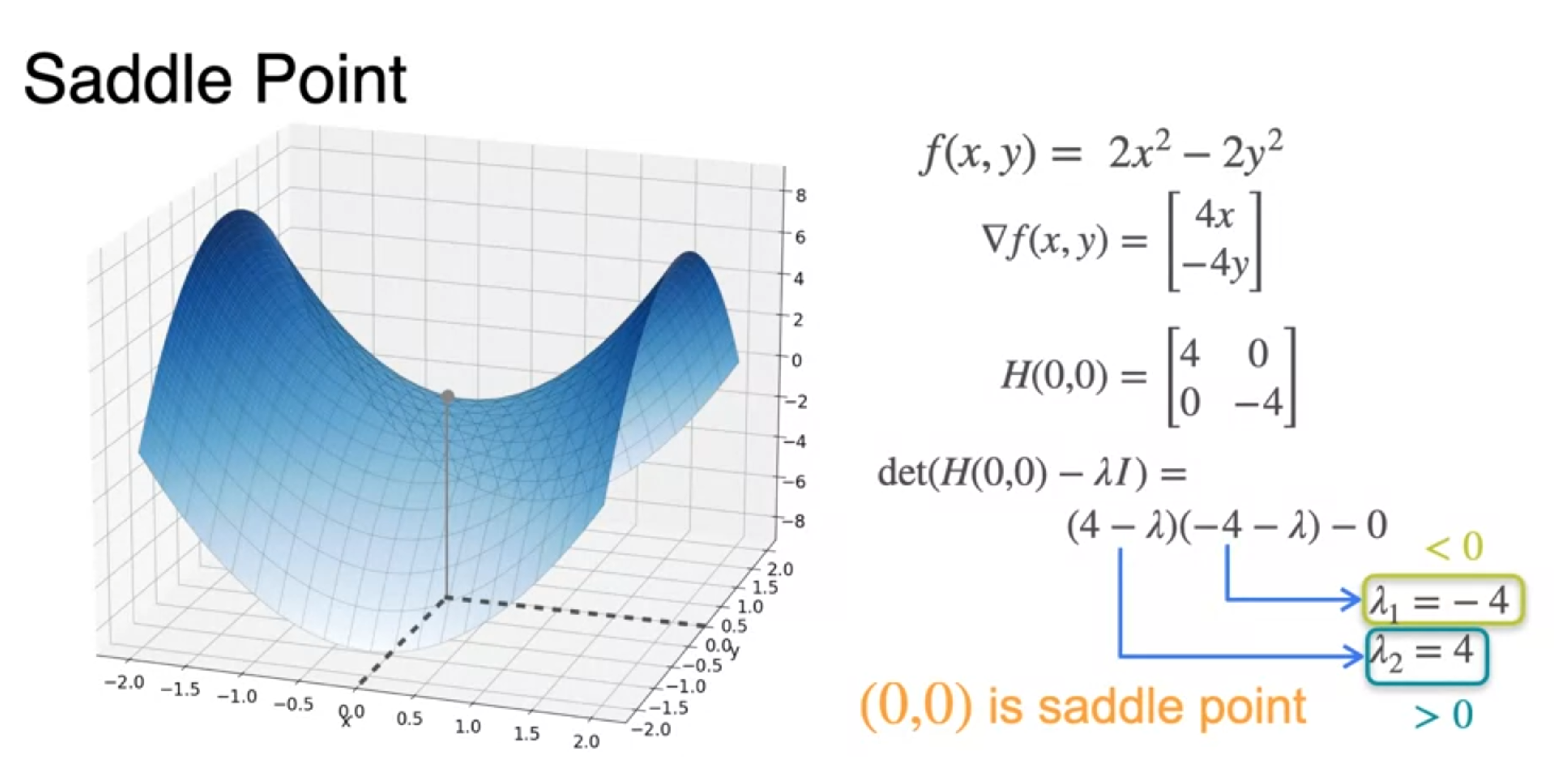
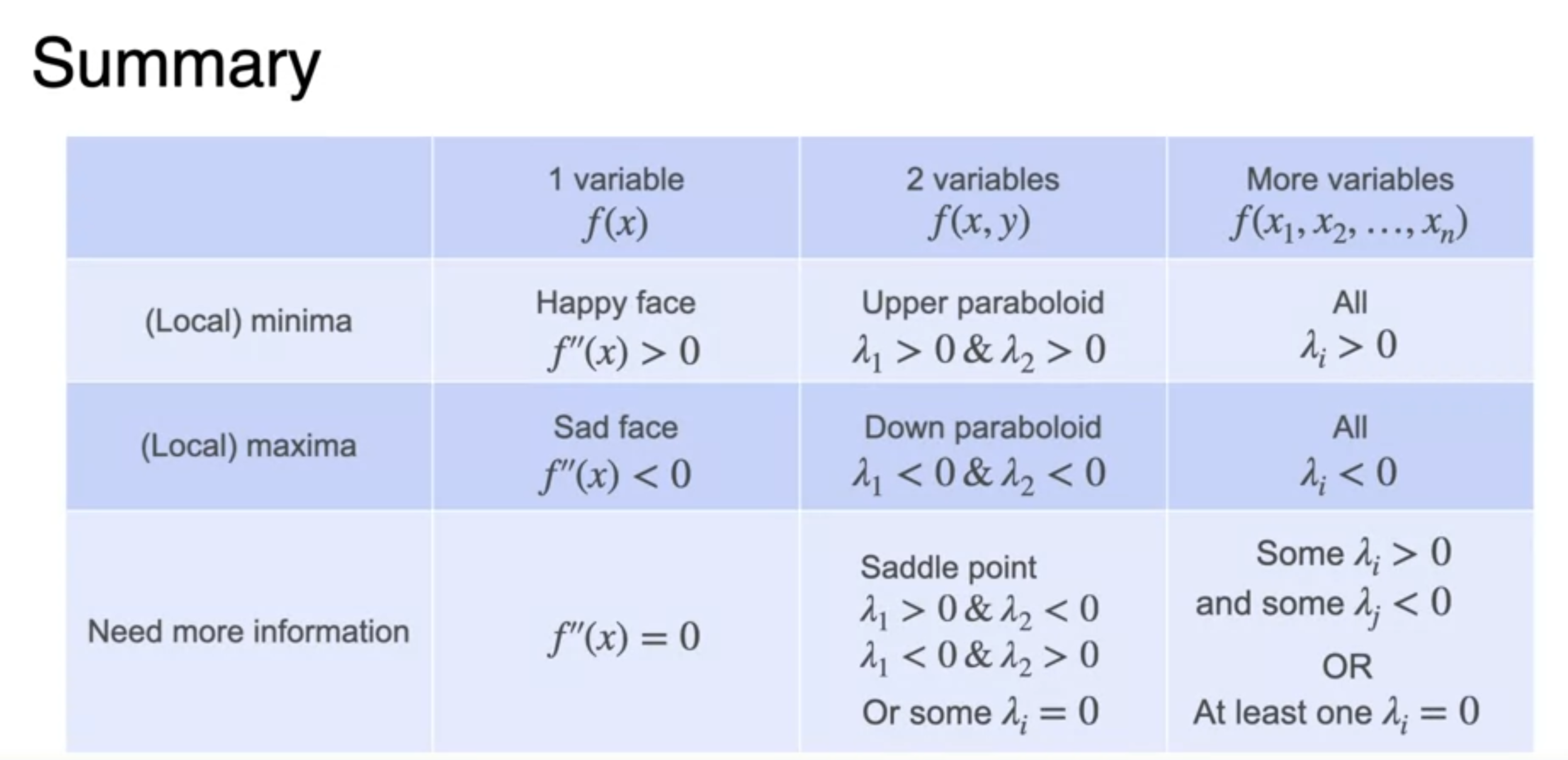
Newton's Method for two variables

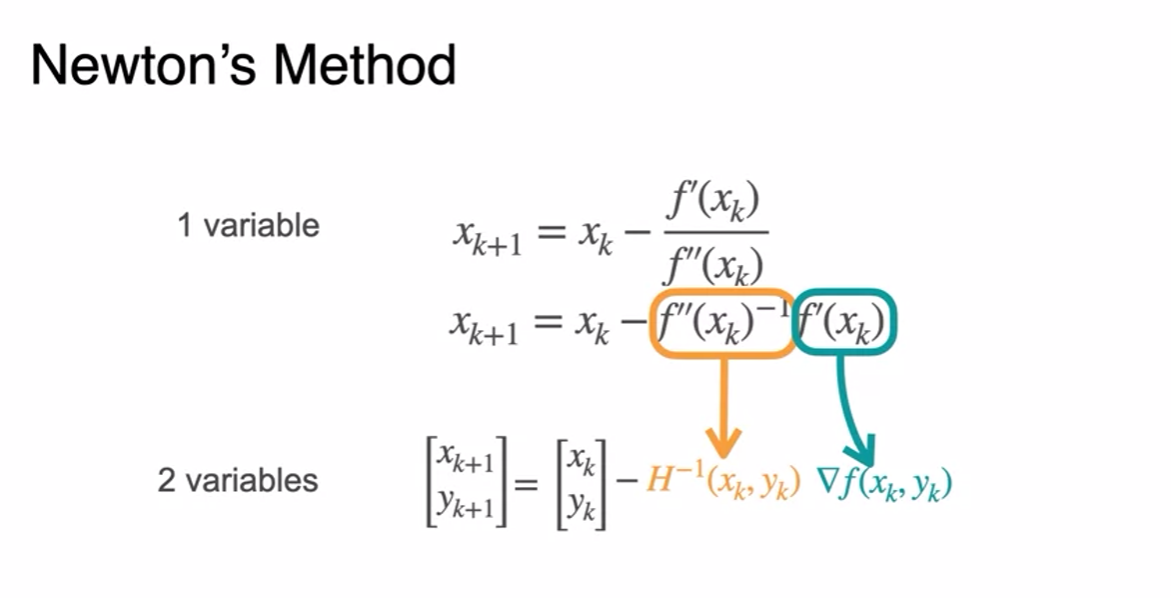
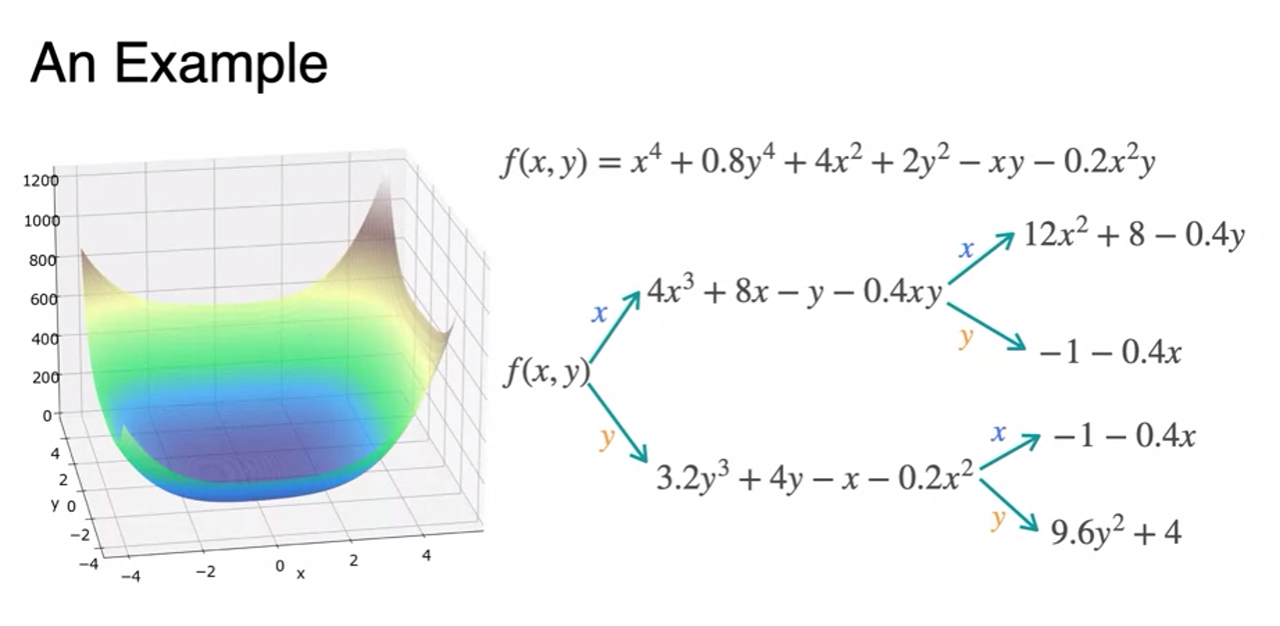
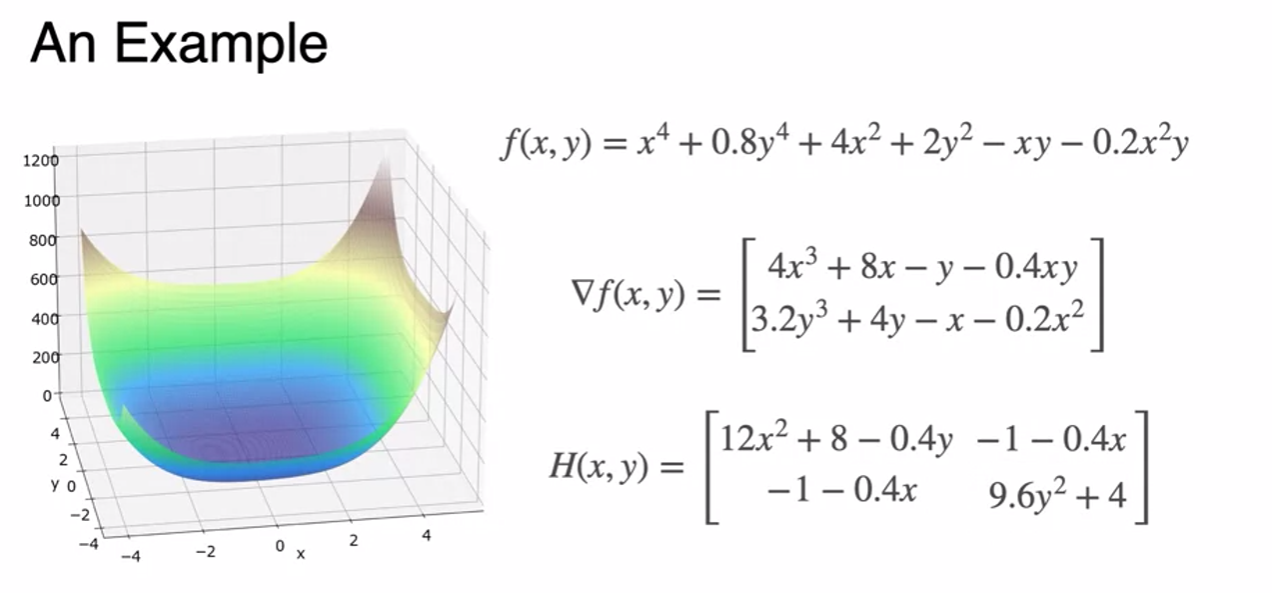
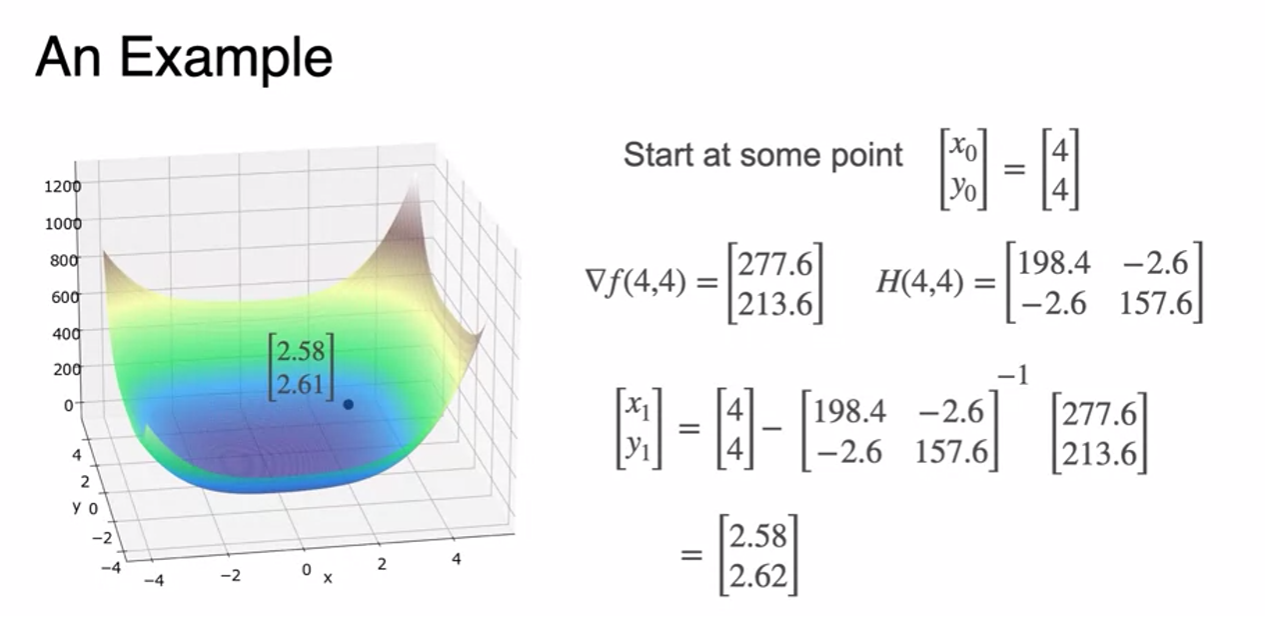
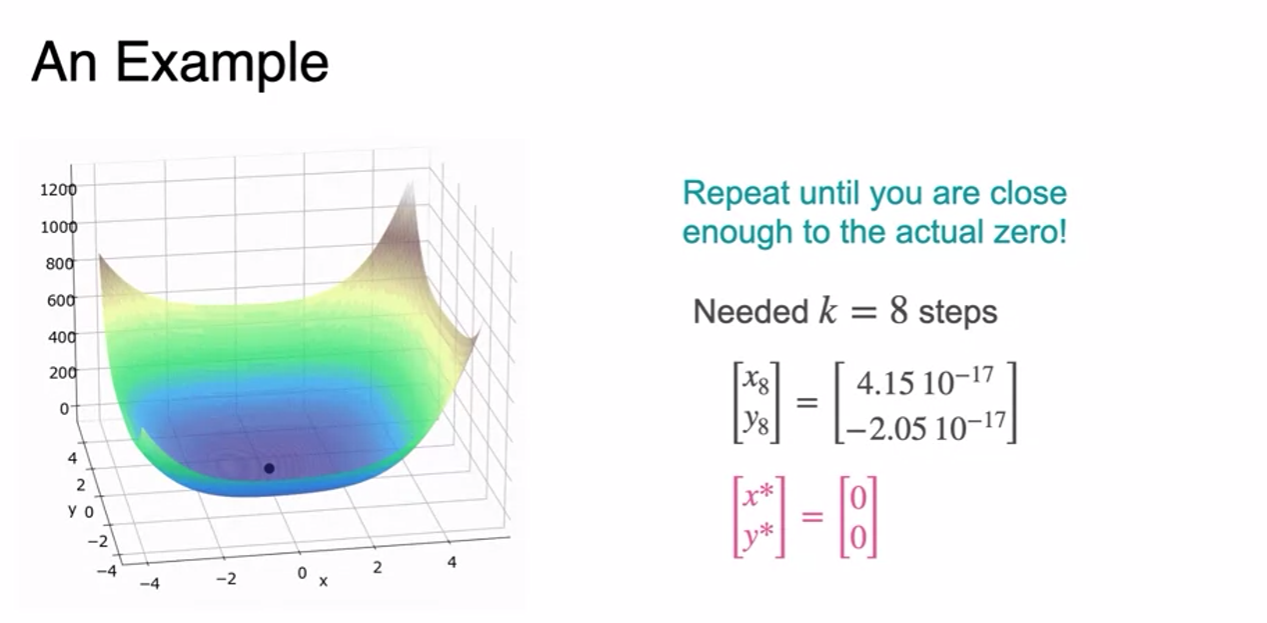
• Only 8 steps to obtain minimum - Fast!