Natural Language Processing - Week 3

Lecture : Vector Space Models

Vector Space Models

Summary

• Represent words and documents as vectors

• Representation that captures relative meaning

Word by Word and Word by Doc.

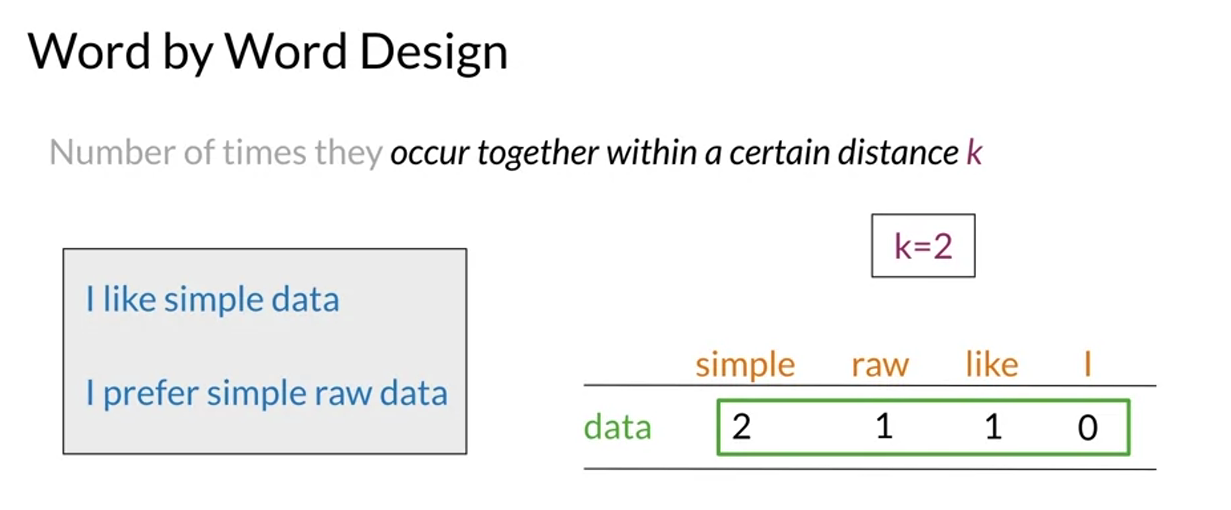
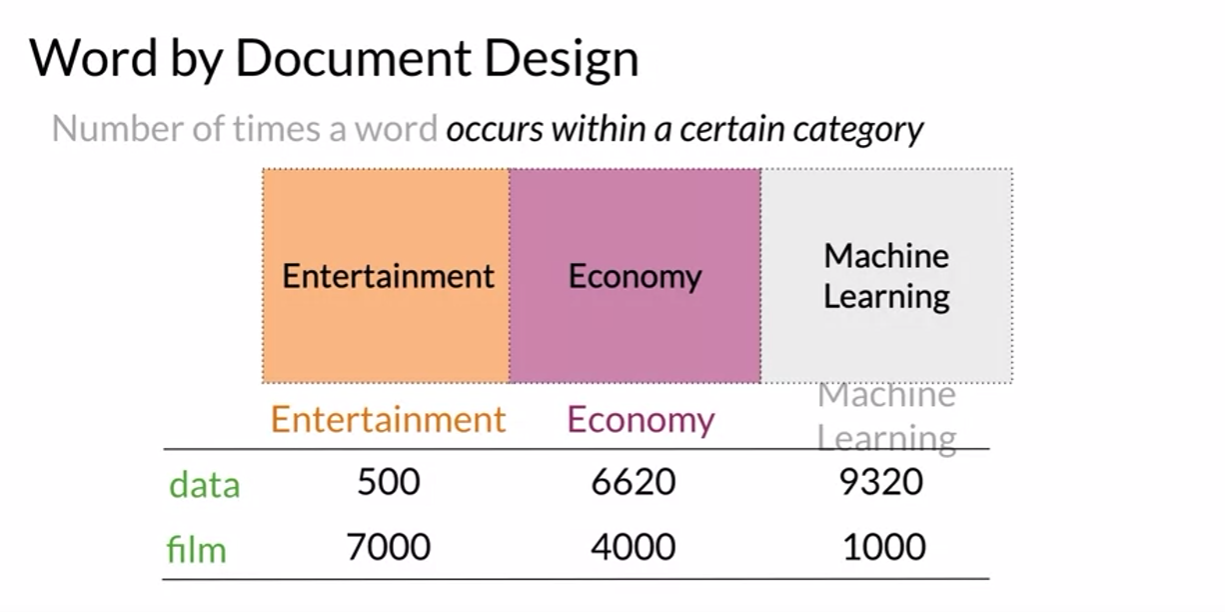
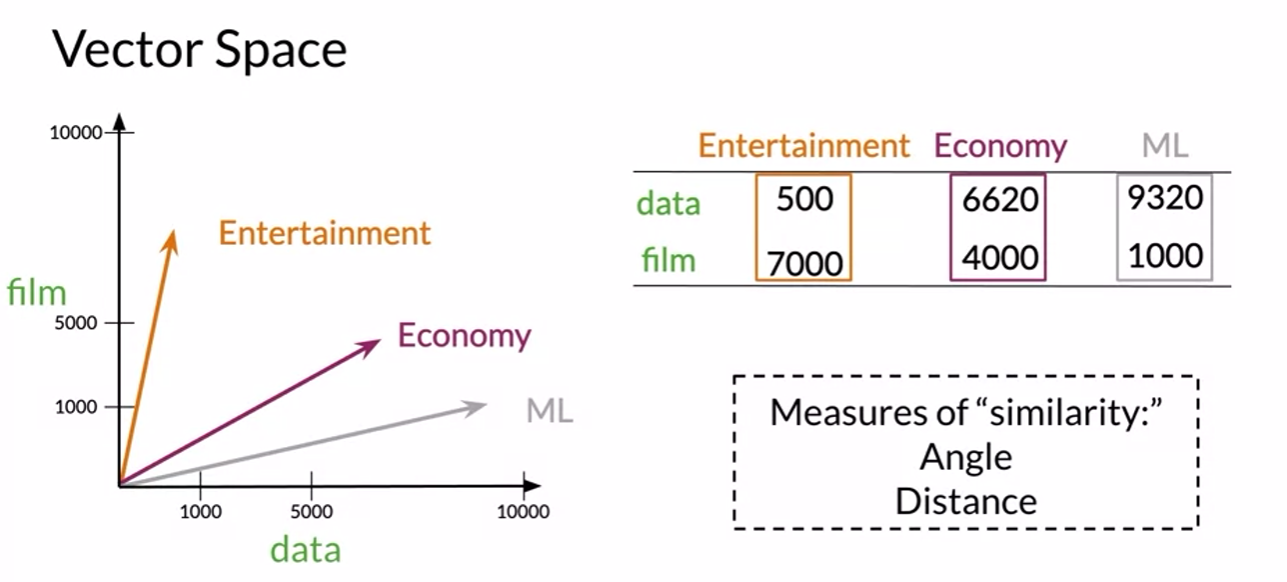
Summary

• W/W and W/D, counts of occurrence

• Vector Spaces -> Similarity between words/documents

Gonna learn about Euclidean distance and Cosin similarity

Euclidean Distance

Summary

• Straight line between points
• Norm of the difference between vectors

Cosine Similarity: Intuition

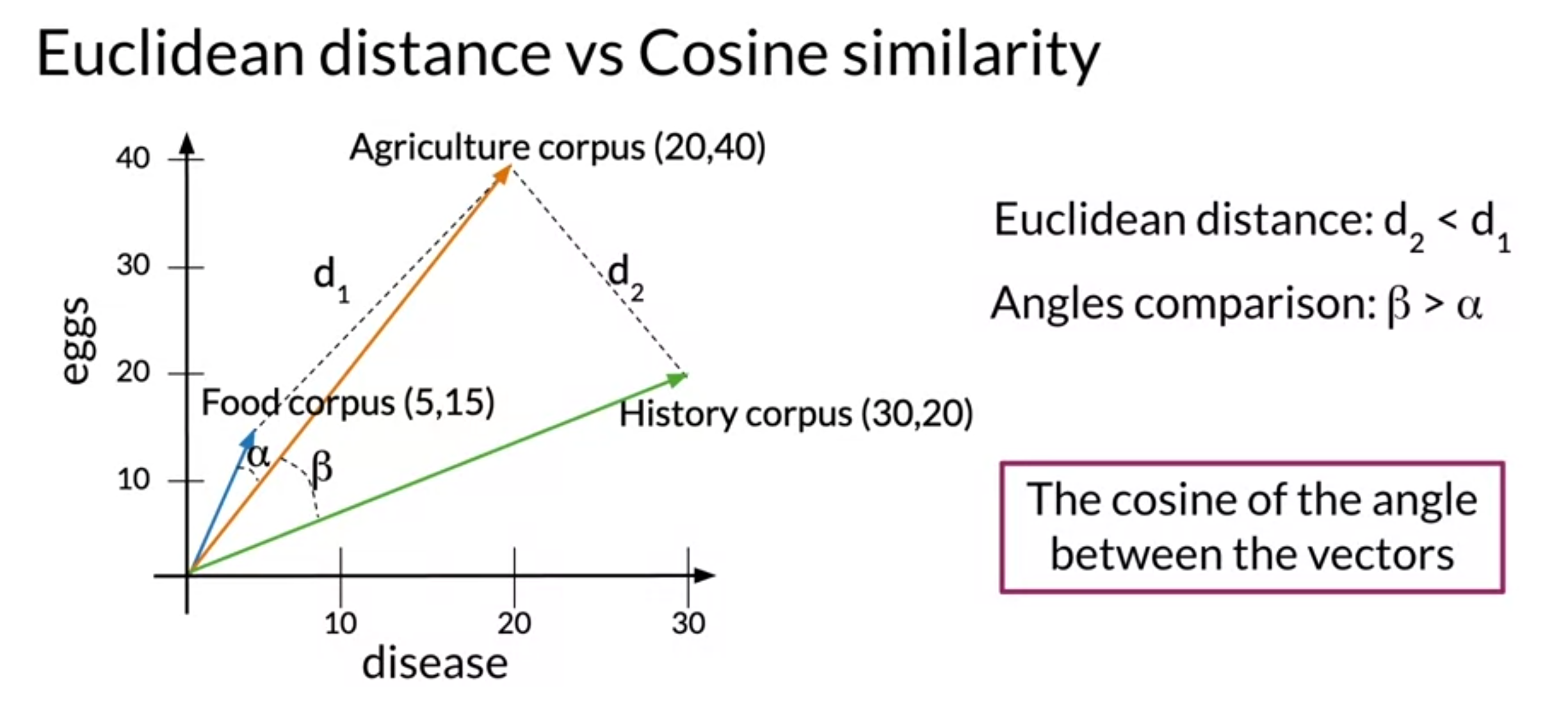
• Cosine similarity might overcome the problem of Euclidean distance
• It isn't biased by the size differences

Summary

• cosine similarity when corpora are different sizes

Cosine Similarity

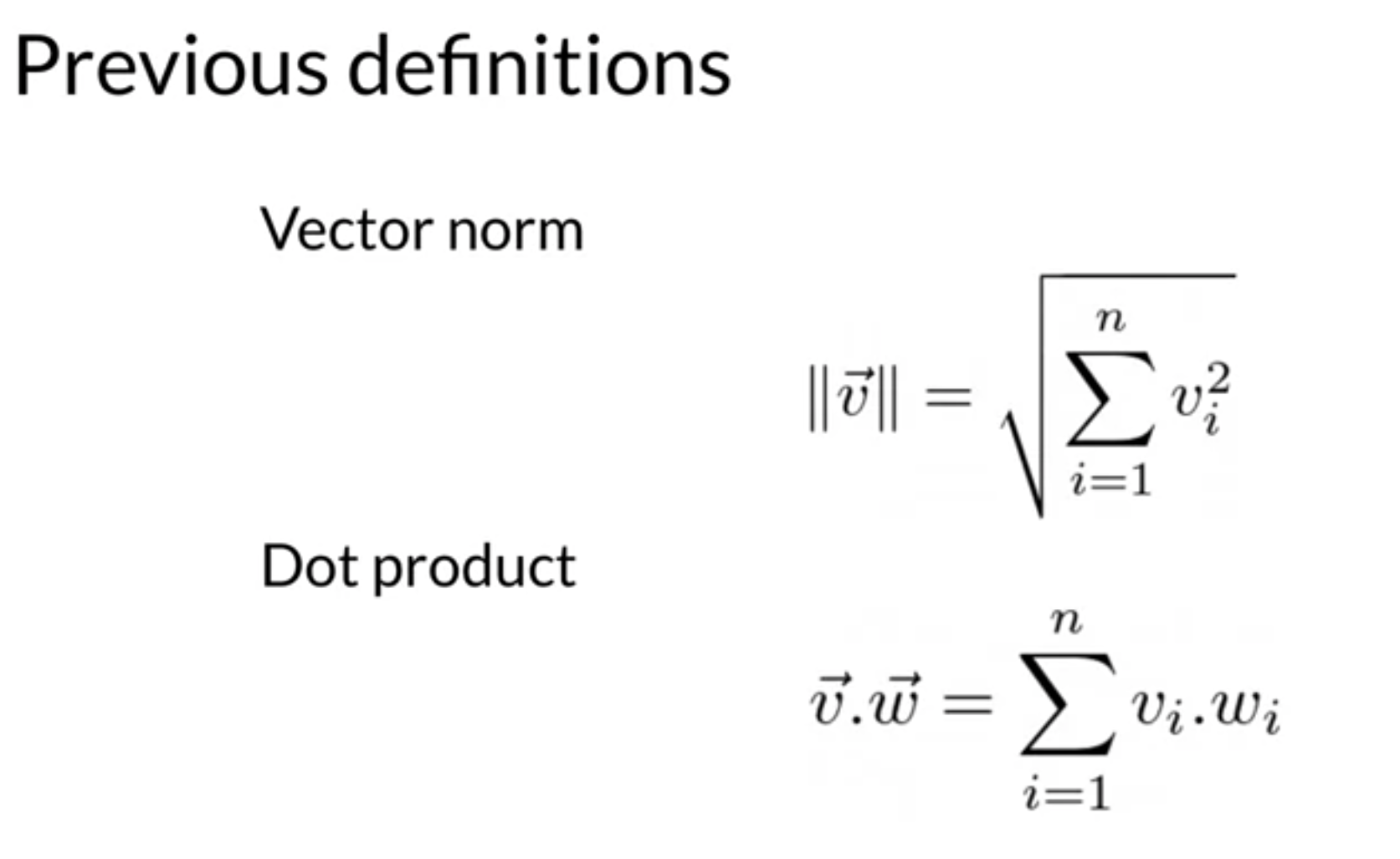
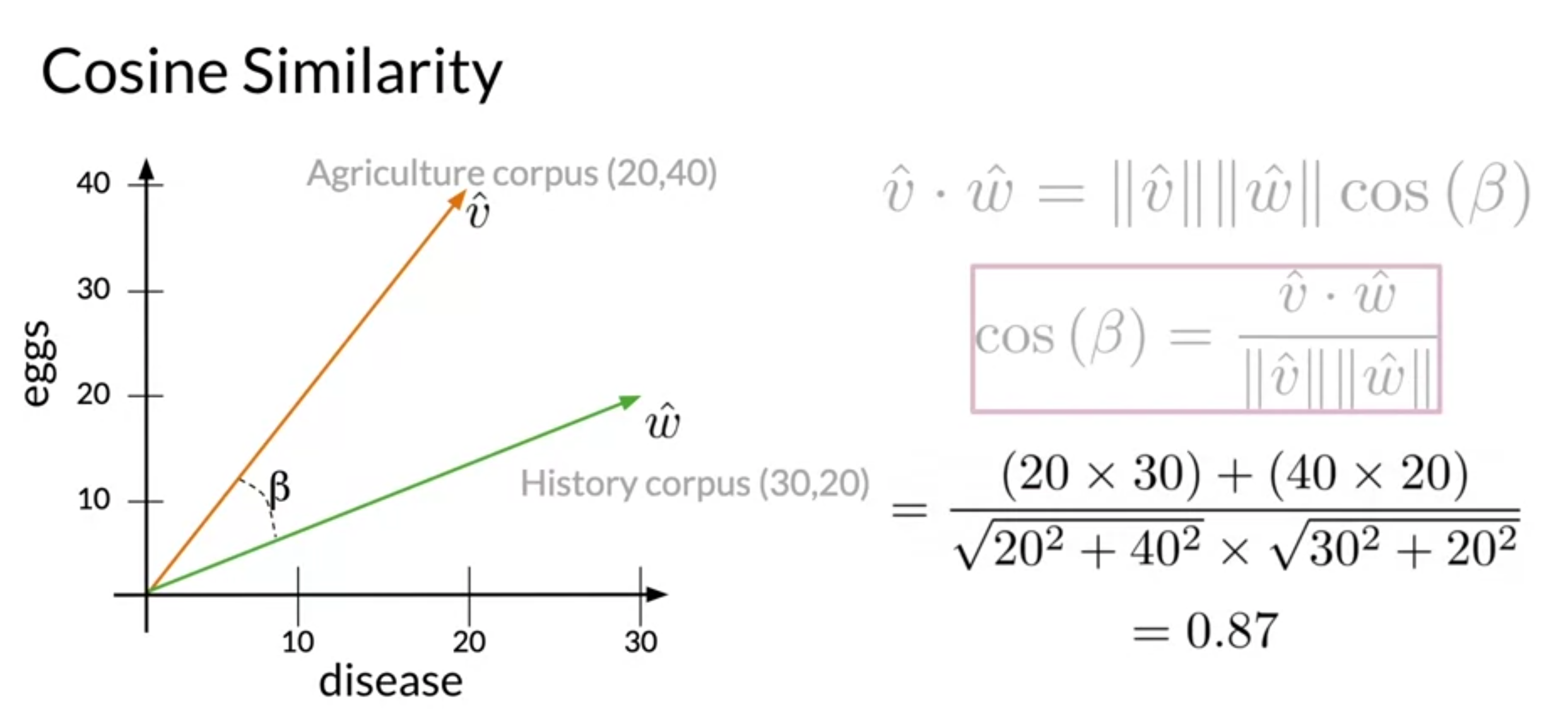
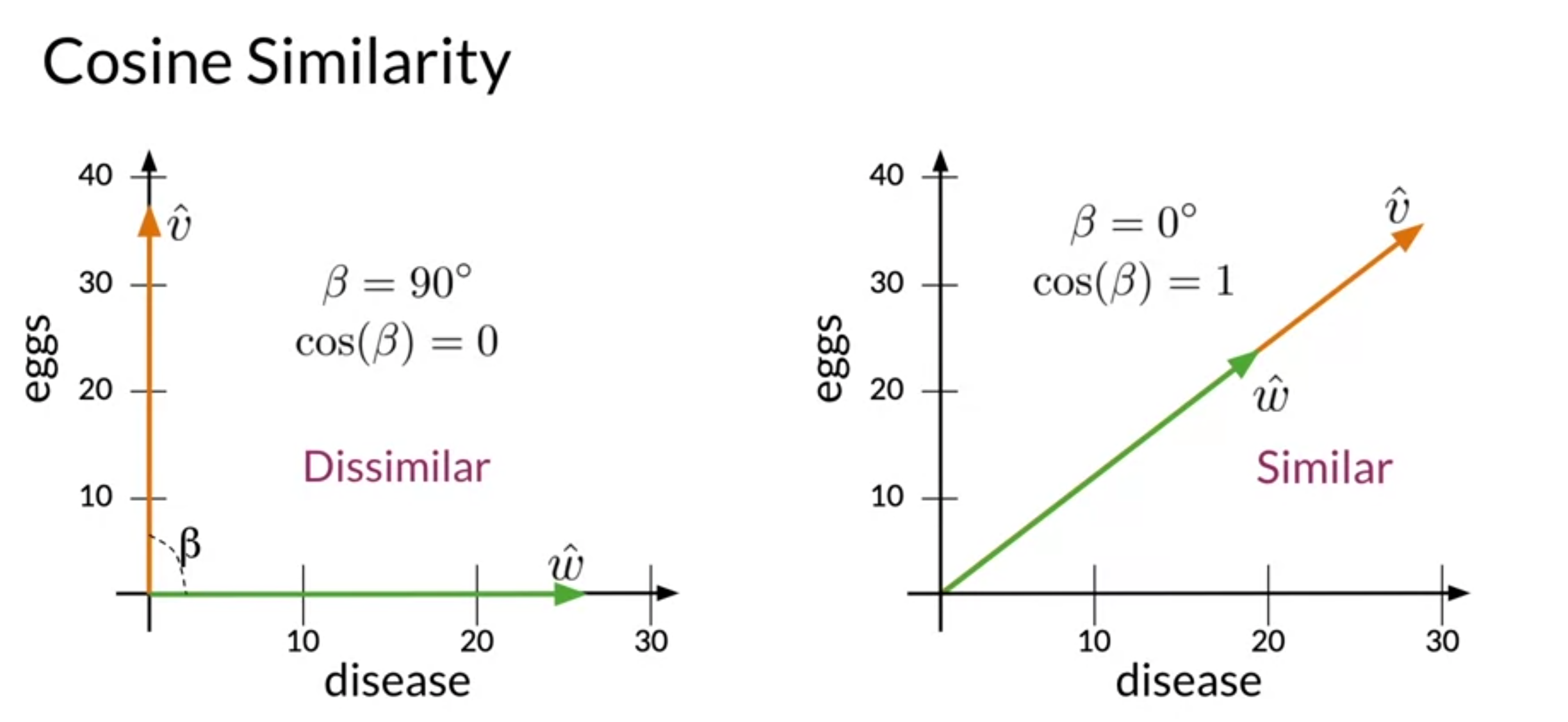
Summary

• Cosine $\propto$ Similarity
• Cosine Similarity gives values between 0 and 1

Manipulating Words in Vector Spaces

Summary

• Use known relationships to make predictions

Visualization and PCA

• use principal component analysis to visualize vector

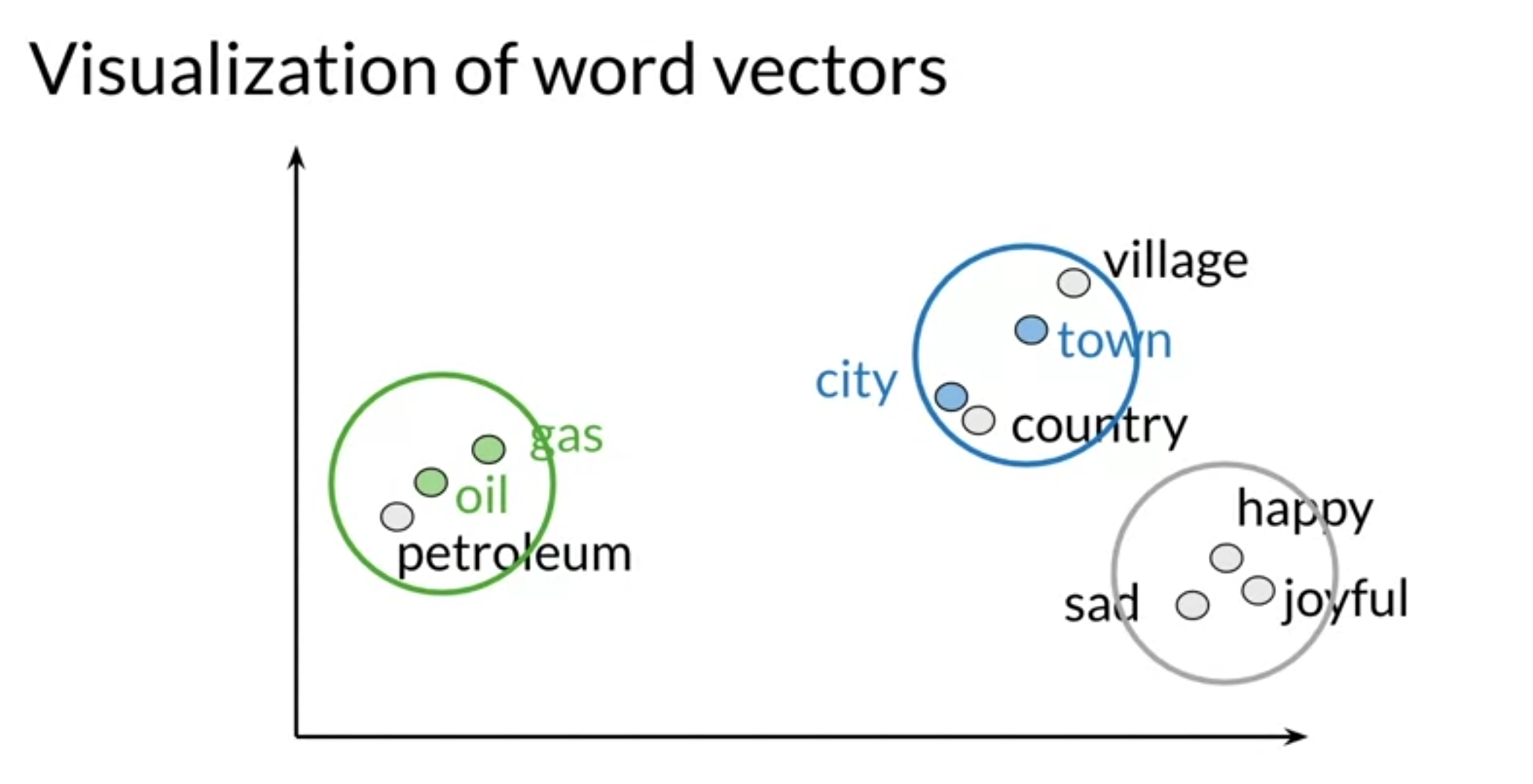
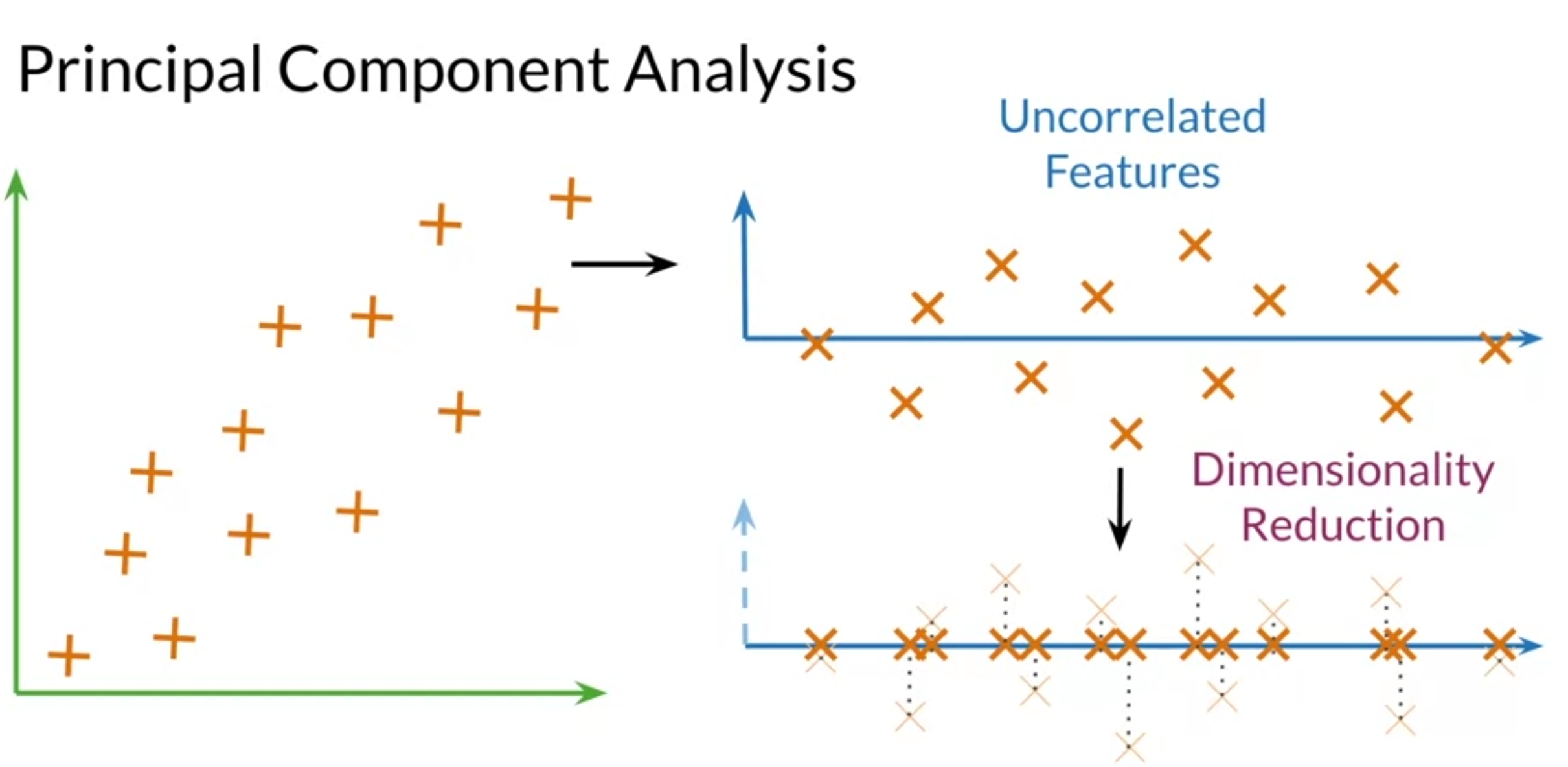
Summary

• PCA : algorithm used for dimensionality reduction that can find uncorrelated features for data

PCA Algorithm

• Eigenvectors give directions of uncorrelated features and t he Eigenvalues are the variants of your data sets in each of those new features.

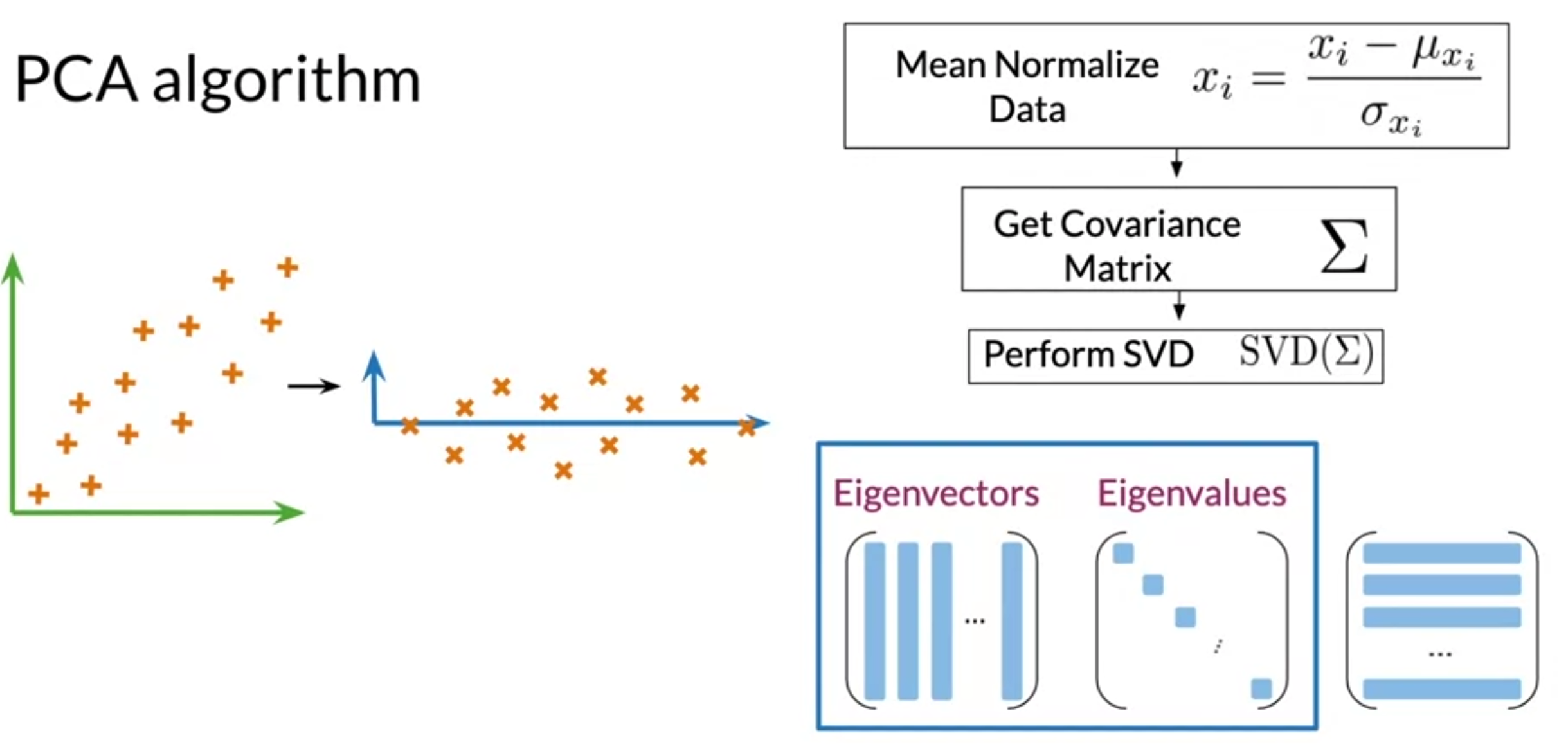
1. get a set of uncorrelated features
   • mean normalize data
   • get covariance matrix
   • perform singular value decomposition

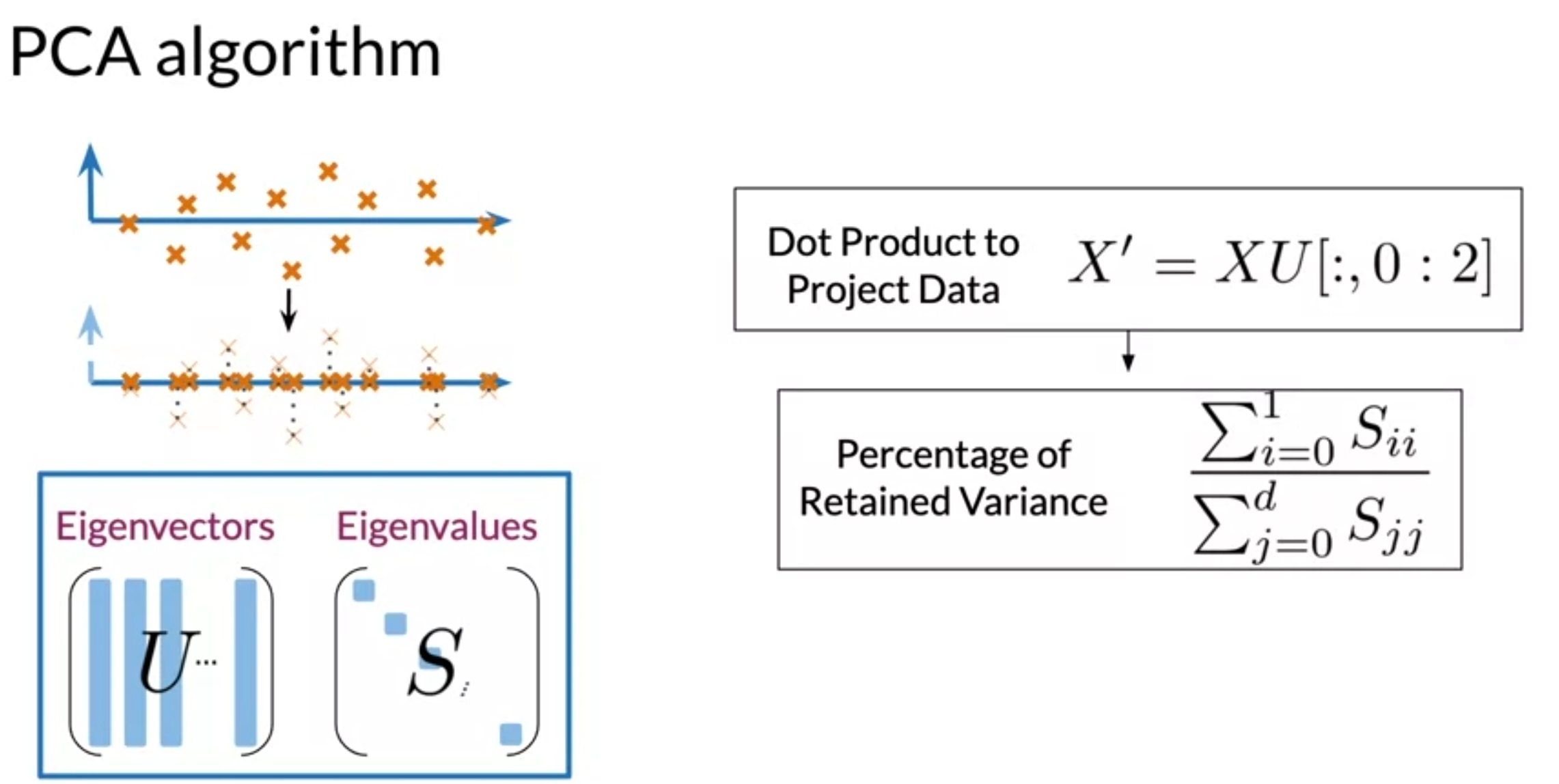
2. project data to a new sets of features
   • perform the dot products between the matrixd containing word embeddings and the first n columns of the U matrix

Summary

• Eigenvectors give the direction of uncorrelated features

• Eigenvalues are the variance of the new features

• Dot product gives the projection on uncorrelated features

Background

• Cov(x,y) = $\frac{\Sigma(x-\bar{x})(y-\bar{y})}{n}$

• $COV_{X,Y} = \begin{pmatrix} Var(X) & Cov(X,Y) \\ Cov(X,Y) & Var(Y) \\ \end{pmatrix}$

  대각선 기준으로 sematric

  

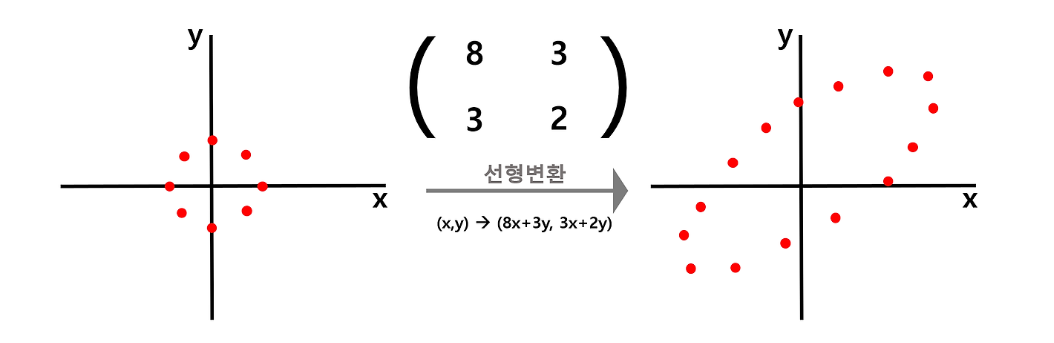
• shearing : covariance matrix를 normal distributed data에 곱하는 것을 선형변환 관점에서 보기도 한다

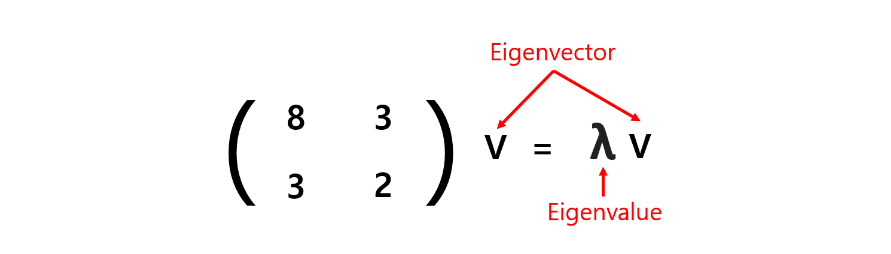
• Linear transform 후에 방향이 같은 vector가 Eigenvector, 길이 변화 비율이 Eigenvalue

• why PCA? : 다중 공신성(multi colinearity)을 해결
  • 데이터의 여러 attributes 중 몇 개가 높은 상관 관계를 가졌을때 그대로 Linear Regression을 하면 그 결과값인 종속변수에 대한 독립변수의 영향력을 신뢰할 수 없어진다.