RL Course by David Silver - Lecture 7: Policy Gradient Methods

Policy Gradient

1. Introduction

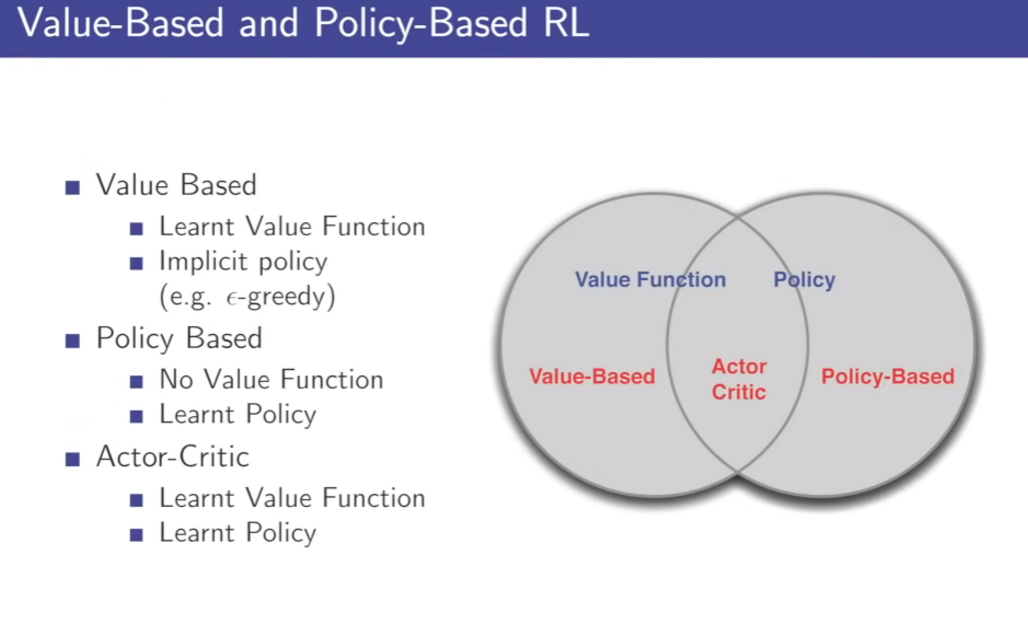
• just follow the gradient we get more reward.
• advantages or disadvnatages of using policy gradient competitive value based method
• why is better idea to work with policy based methods than value based methods
  • some situation value function might be more complicated. policy will be more compact

• what if vast action space

  • solve complicated maximization every step
  • use policy based method

• disadvantage :

  • naive policy based RL might be slower, higher variance, less efficient than value based method
  • value based method move absolutely what you estimate best policy
  • gradient policy method move little

• this is the case
  • optimal policy : play random
  • optimal behavior is stochastic; stochastic policy is necessary

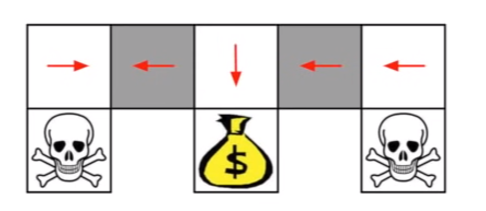
• in deterministic policy you pick the same action in those two grey states
• it taakes long to reach the tresure until you take $\epsilon$ from middle
• value based method

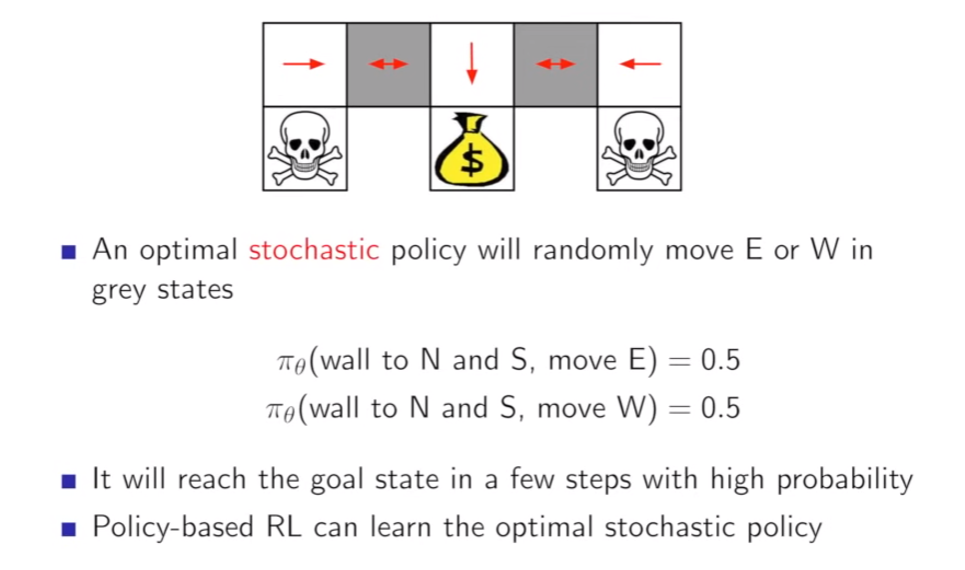
• stochastic policy is much better than deterministic one

• how to optimize policy
  • first : which start value reach to best
  • second : average all rewards from each state
  • third : some probability that Im in a state, some probability I'll take action from that state under my policy; immediate reward at that step

• you know gradient method will point to the direction how to do better in this MDP rather than try and error

2. Finite Difference Policy Gradient

• we want to higher our objective function

• this is naive numerical approch

• We want to take the gradient of our policy
  and want to take expectations of that thing
  • loglikelihood; we can multiply and devide by our policy without changing it
• gradient policy divided by the policy equal to the gradient of the log of the policy
  • $\frac{\nabla_\theta \pi_\theta(s,a)}{\pi_\theta(s,a)}$
  • $\nabla_\theta log\pi_\theta(s,a)$

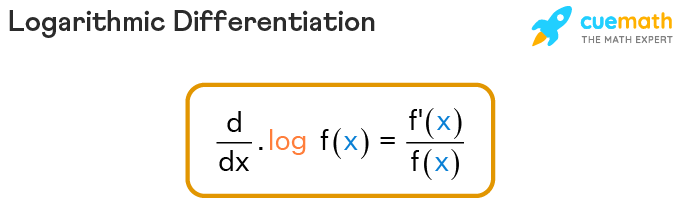
• discrete action

-continuous action space

• parameterize the mean of Gaussian

• we take an action $a$ from a given state $s$, we compute the gradient of this log policy $\nabla_\theta log\pi_\theta(s,a)$, we multiply it by the immediate reward $r$ that we actually experienced

  • gives us gradient step
  • model free

• how about multi step mdp?

• replace immediate reward $r$ with the value function $Q^{\pi_\theta}(s,a)$ (the long term reward)

• policy objective function이 뭐던간에

  • $J$ = $J_1, J_{avR}, \frac{1}{1-\gamma}J_{avV}$
    policy gradient는 $\nabla_\theta J(\theta) = \mathbb{E}_{\pi_\theta}[\nabla_\theta log\pi_\theta(s,a) Q^{\pi_\theta}(s,a)]$

• 만약 Supervised learning이라면 Value function이 없고 adjusting major policy to the direction of what teacher tells you

3. Monte-Carlo Policy Gradient

• forward view algorithm
  • Gt is the returned accumulated rewards from that time step on

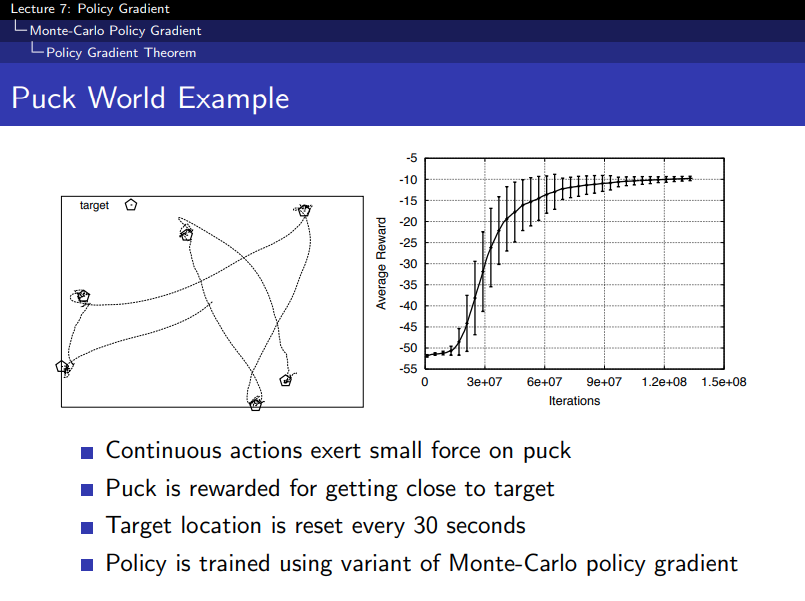
• value based RL usually more jaggy but its more smooth

• slow and very high variance

• rest of lecture learn what is more efficient way

4. Actor-Critic Policy Gradient

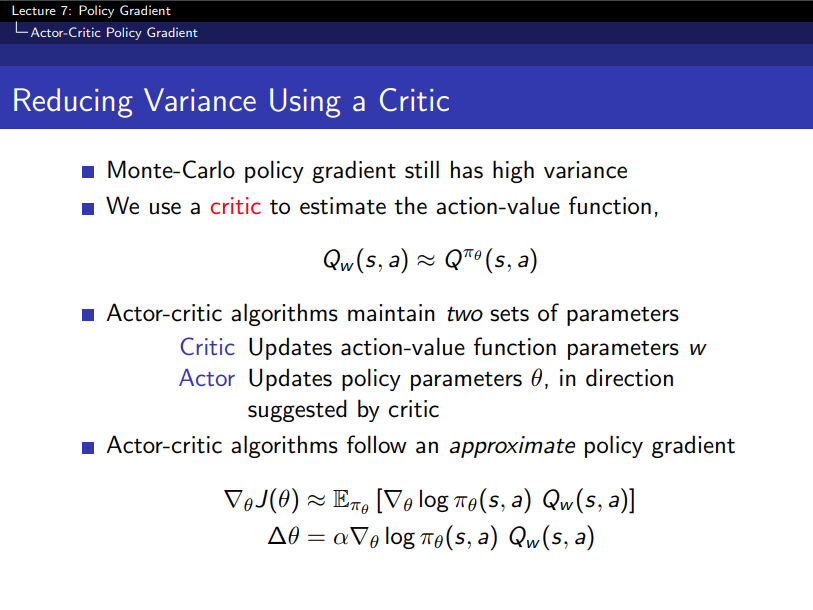
• start off with a arbitrary policy and evaluate that policy using the critic and then instead of greedy policy improvement we're moving a gradient step in direction to get a better policy

• value-function - value based

• policy - policy based

  • both of them - actor-critic

• 파라미터를 reward많이 얻는 action을 선택하는 policy가 되도록 업데이트